基于小波变换和证据理论的多传感器融合诊断

向阳辉，朱宗铭

（长沙学院机电工程学院，湖南 长沙 410022）

由于机械设备的大型化和复杂化，单传感器所反映的设备信息具有不确定性。这种不确定性的存在必然导致故障诊断准确率的降低，甚至出现漏报和误报现象［1］。多传感器信息融合技术具有独特的多维信息处理方式，在解决设备故障诊断不确定性问题时具有显著的优势，可以大幅提高机械设备故障诊断的准确率［2-3］。在设备故障诊断中引入多传感器信息融合技术已成为本领域的研究热点［3-5］。

小波变换是继傅里叶变换后的一种新的时频分析方法，具有较好表征信号局部特性的能力［6-7］，是故障信号分析和故障特征提取的较理想工具；而证据理论作为一种重要的不确定推理方法，在多传感器信息融合故障诊断中得到了广泛的应用［8-10］。但如何将小波变换和证据理论相结合以进行多传感器信息融合故障诊断，如何构造各局部诊断的概率分配，如何避免各局部诊断证据之间的严重冲突，至今没有统一有效的解决方案。

鉴于此，文章基于小波变换提取各传感器振动信号的小波能量特征向量，将其与典型故障模式进行贴近度分析，获得各传感器局部诊断的基本概率分配，再通过Lance距离分析对各传感器局部诊断证据赋予不同可信度的权重，并基于证据理论对多个传感器局部诊断证据进行加权融合，实现多传感器故障诊断的决策级融合，从而提出了一种基于小波变换和证据理论的多传感器信息融合故障诊断方法，最后通过算例分析验证了文章方法的有效性。

1 多传感器信息融合故障诊断模型

多传感器信息融合故障诊断的应用框架如图1所示。

图1 多传感器信息融合故障诊断流程

步骤1：进行小波变换，提取各传感器信息的故障特征参数。根据待诊断设备现场实际情况安装多个传感器进行振动信号采集，将采集到的信号进行小波变换以提取各层的小波能量参数，将其构成小波能量特征向量，用以表示设备当前故障特征。

步骤2：进行贴近度分析，构造各传感器局部诊断证据的基本概率分配。每一个传感器都看作是一个独立的局部诊断证据体，将每一个传感器提取的小波能量特征向量与典型故障模式进行贴近度分析。通过计算各个传感器小波能量特征向量与典型故障模式标准小波能量特征向量的贴近度，实现各传感器局部诊断证据基本概率分配的有效构造。

步骤3：通过Lance距离分析，赋予各传感器局部诊断证据不同的可信度权重。基于各传感器证据体之间的Lance距离矩阵，计算各传感器证据之间的相似度矩阵，根据相似度矩阵计算各传感器证据的可信度，并将其作为各传感器局部诊断证据的权重系数。

步骤4：基于证据理论进行多传感器局部诊断证据的加权融合诊断合成。根据各传感器证据不同的可信度权重对各局部诊断的基本概率分配函数进行加权修正，并利用证据理论的多证据组合规则进行合成，从而计算得到多个传感器局部诊断证据加权融合诊断合成后对各故障模式的可信度和不确定度。

步骤5：进行故障诊断决策，得出最终诊断结论。根据故障诊断的决策法则，将多个传感器证据加权融合诊断合成后，对各故障模式的可信度和不确定度进行分析，并选择恰当的参数（ε，γ），综合判定最终的故障模式。

2 小波变换与单传感器局部诊断

2.1 基于小波变换的特征提取

小波变换是时频分析方法，时变信号f(t)∈L2(R)，其小波变换计算公式为：

其中，ψa,b(t)为小波基函数，其表达式为：

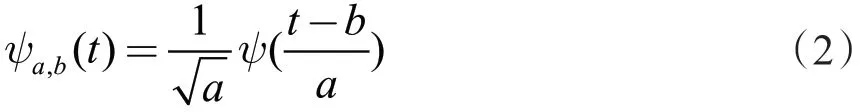
式中：a为尺a度因子；b为平移因子。

Mallat算法是正交小波分解的快速算法［7］。小波变换在工程实际应用分解时，需要进行离散化处理。基于多分辨率分析理论，离散小波变换的Mallat分解算法为：

式中：kn= 0,1,2,…,N-1；N为采样点数；j为小波分解层数；fk为时域信号波形；h（n）、g（n）为共轭镜像滤波器的H和G脉冲响应。

小波分解每次都是把信号分解为2个子信号。若信号频率对应[0,ωm]，分解后子信号频率分别为，这2个信号分别为逼近信号和细节信号。小波变换的Mallat分解可以提取故障信号的频域特征［7］。

利用Mallat分解算法对各传感器振动信号J层正交小波分解和重构［7］，其小波能量特征向量为：

该小波能量特征向量E可以用来表示各传感器振动信号当前故障的频域特征。

2.2 基于贴近度分析的局部诊断

要想准确可靠地诊断设备的故障类型，需要将该传感器检测信号的小波能量特征向量与典型故障库中的标准小波能量特征向量进行对比，分析它们之间的贴近度，再通过贴近度分析和归一化处理，实现各传感器证据的局部诊断，并构造出各传感器证据的基本概率分配函数m（A）。

将待诊断传感器信号的小波能量特征向量E设为模糊向量，再用Xi表示典型故障库中第i种故障的标准小波能量特征向量。Ej为模糊向量的第j个分量；Xij为第i种故障模式标准特征向量的第j个分量。贴近度σi表示比较待诊断模糊向量E与何种故障的标准特征向量Xi最贴近，其贴近度σi计算公式为：

贴近度σi越大，表明该种故障发生的概率越大。对贴近度的平方值进行归一化处理，以此作为该传感器证据局部诊断的基本概率分配函数m（Ai），其计算公式为：

3 证据理论与多传感器融合诊断

3.1 D-S证据理论基础

假定某待检测设备系统的相互独立的所有可能故障模式为N种，其集合为辨识框架Θ={A1，A2，…，An}，Ai称为Θ的基元，2Θ为Θ的幂集。集函数映射如果满足m：2Θ→［0，1］，则称该映射为基本概率分配函数。其中：

对于∀A⊆Θ，m（A）称为A的基本概率分配。对辨识框架Θ定义为：

称映射Bel：2Θ→［0，1］为辨识框架Θ的信任函数，映射Pl：2Θ→［0，1］为辨识框架Θ的似真度函数。将［Bel（A），Pl（A）］称为A的信任区间，信任区间是用来描述当前证据体对故障模式A的信任的上限和下限，信任区间的长度表示对故障模式A的不确定度。

3.2 基于Lance距离的证据可信度分析

Lance距离可以用来有效度量多个证据间的证据距离，是证据理论在工程实际应用过程中处理证据严重冲突的可靠方法［11］。

假定某待检测设备系统N种故障模式的辨识 框 架Θ={A1，A2，…，An}共 有K个传感器证据m1,m2,…,mk，其对应的基本概率分配函数为。则mi和mj之间的Lance距离定义为：

将各个传感器证据之间的Lance距离组合构成Lance距离矩阵D，定义如下：

i=j表示证据自己与自己进行比照，d(mi,mj)=0表明证据之间没有距离。

用相似度s（mi，mj）来度量传感器证据体mi和mj之间的相似程度，定义为：

相似度矩阵S定义为：

s（mi，mj）值越大，表示证据体mi与mj的一致性程度越高。因此可以分别计算各传感器证据体mi的被支持程度zi：

将传感器证据体mi的被支持程度zi与所有传感器证据中的最大被支持程度进行比较，即可定义该传感器证据体mi的可信度权重系数ωi：

高楼村的变化，仅是该镇开展“四美乡村”“五美庭院”“美丽小镇”建设的一个缩影。按照“试点先行、示范带动、全面铺开”的思路，该镇优先打造了高楼、水寨、张楼、新庄4个示范村，通过典型引路，连点成线、连线成片、集片成群，形成美丽乡村建设的 “雁阵效应”和改善农村人居环境工作的“特色品牌”。

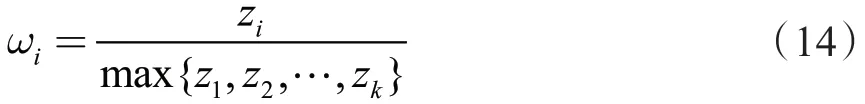
3.3 多传感器证据的加权融合诊断

为了在多传感器证据融合诊断时充分考虑各证据体的不同可信度，根据证据体的权重系数ωi，对各个传感器证据体的基本概率分配m（Ai）进行加权修正。对于∀A⊆Θ，则定义如下：

设m1'和m2'是辨识框架上的加权概率分配函数，基元分别为B1，B2，…，Bn和C1，C2，…，Cn。若∀A⊆Θ，将m1'和m2'进行合成后，加权概率分配函数为：

其中：

式（16）的组合称为正交和，记为m12。P为规范数，它是把空集上的信任度成比例分配到非空集，从而满足证据组合时概率分配的要求。P值能够反映两个证据之间的冲突程度，当证据冲突越大时，P越小。当两证据严重冲突时，证据合成的规则将不再有效。文章基于各传感器证据的可信度先对各证据体进行了加权处理，使各传感器证据之间的冲突得到了明显降低，从而保障了基于多传感器证据的加权融合故障诊断合理有效。

由于多个证据之间组合不受运算次序的影响，因此K个传感器证据之间的组合可以用两个证据的组合规则递推得到：

4 算例分析

文章算例是基于转子实验台分别模拟不平衡、不对中、支座松动、动静碰摩和油膜涡动5种典型工况故障模式，进行多传感器信息融合故障诊断识别研究。实验台的转速设为1 000r·min-1，在实验台转轴水平方向布置4个Bently 3 300XL8mm电涡流传感器测点，用于监测实验台转轴的水平振动情况和采集信号。由于实验室采集到的各典型故障模式的振动信号都比较理想，为了使实验模拟更符合实际工况，文章所有传感器采集到的信号都加入了占幅值13%左右的白噪声信号。

文章诊断系统的辨识框架为Θ={F1，F2，F3，F4，F5}，其中F1为不平衡状态，F2为不对中状态，F3为支座松动状态，F4为动静碰摩状态，F5为油膜涡动状态。将每个传感器都分别作为多源信息融合故障诊断的一个独立证据体，4个传感器分别为4个局部诊断独立证据体。我们先对每个传感器的振动信号进行小波变换，用db10小波进行6层小波分解，提取信号的频域小波能量特征向量(E0,E1,E2,…,E6)，再与典型故障库中的故障模式的小波能量标准特征向量进行贴近度分析和基本概率分配。文章直接参考文献［7］给出的典型故障的小波能量标准特征向量，如表1所示。

表1 典型故障的小波能量标准特征向量

在转子的不平衡状态（F1）下，分别提取4个传感器振动信号的频域小波能量特征向量，如表2所示，根据式（5）计算得到各传感器证据对各故障模式的贴近度，如表3所示。

表2 各传感器信号的频域小波能量特征向量

表3 各传感器证据对各故障模式的贴近度

根据式（6）计算得到各传感器局部诊断证据对各故障模式的基本概率分配，如表4所示。

表4 各传感器证据对各故障模式的基本概率分配

对各证据的基本概率进行分析，并根据式（9）（10）计算得到各传感器局部诊断证据之间的Lance距离矩阵D：

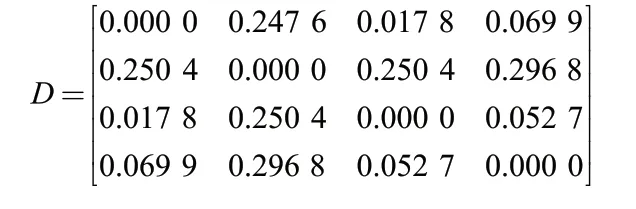
根据式（11）（12）计算得到各传感器局部诊断证据之间的相似度矩阵S：

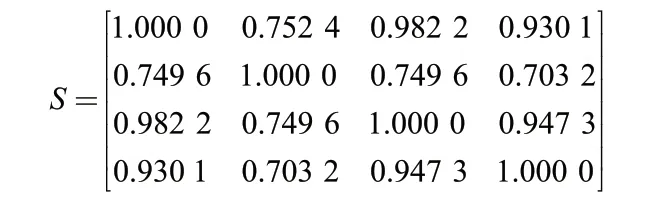
根据式（13）（14）计算得到各传感器局部诊断证据的可信度权重系数，如表5所示。

表5 各传感器证据体的权重系数

根据式（15）计算得到各传感器证据对各故障模式的加权概率分配，如表6所示。

表6 各传感器证据对各故障模式的加权概率分配

从表3可以看出，2号传感器证据偏向于支持故障模式F4，明显与真实故障工况不符，可能是2号传感器在信号测量与分析过程中受到了强噪声干扰等情况，产生了错误诊断结果。因此，在多传感器融合诊断的过程中需要将证据体2进行弱化，尽可能降低其对故障综合诊断结果的负面影响。

表4中2号传感器证据对非真故障模式F4基本概率分配为0.411 4，表5中基于Lance距离分析确定2号传感器证据的可信度权重为0.822 5。通过对所有证据都进行可信度加权处理得到各传感器证据的加权概率分配（见表6），可以发现2号传感器证据对非真故障模式F4加权概率分配下降到了0.338 4，对错误诊断起到了一定的抑制作用。

根据式（18），分别计算得到经典D-S多传感器证据组合识别的概率输出，如表7所示。文章多传感器证据组合识别的加权概率输出如表8所示。

表7 经典D-S多传感器证据组合识别的概率输出

表8 文章多传感器证据组合识别的加权概率输出

续表

从表7中可以看出，当2个传感器证据进行融合诊断时，结果并不一定可信，如证据组合1-2、2-3、2-4的诊断结果与真实故障工况不太符合；当3个传感器证据进行融合诊断时，结果都趋向于支持真实故障模式F1；当4个传感器证据（1-2-3-4）进行融合诊断时，对真实故障模式F1的概率输出大幅提升，达到0.793 6。由此可见，融合诊断时的传感器证据数量越多，结果可信度越高。基于多个传感器进行融合诊断能够有效提升对真实故障模式的概率输出。

从表8中可以看出，利用基于各传感器证据之间的Lance距离先对各证据的基本概率进行加权处理，再将多个传感器证据的加权概率输出进行融合诊断，其结果对真实故障模式的概率分配明显提升，对非真故障模式的概率分配明显下降。如证据组合1-2对真实故障模式F1的概率分配从0.313 2提升至0.384 1；证据组合1-2-3对真实故障模式F1的概率分配从0.544 6提升至0.632 4；证据组合1-2-3-4对真实故障模式F1的概率分配从0.793 6提升至0.831 8。由此可见，多传感器证据加权融合后的故障诊断结果具有更明显的区分度和峰值性，能够有效提升多传感器融合诊断系统的故障识别能力。

5 结论

（1）文章基于小波变换提取各传感器振动信号的频域小波能量特征向量，并将其与典型故障模式的标准小波能量特征向量进行贴近度分析，有效实现了各传感器局部诊断的基本概率分配。

（2）文章基于Lance距离对各传感器局部诊断证据的可信度进行了分析和权重系数确定，并结合证据理论对多传感器证据进行了加权融合。融合诊断对真实故障模式的概率输出明显提升，对非真故障模式的概率输出明显下降。

（3）为了合理融合待诊断设备的多个传感器信息来有效提高故障诊断的准确率，文章提出了一种基于小波变换和证据理论的多传感器融合故障诊断方法，算例分析表明，多传感器融合故障诊断结果具有更好的区分度和峰值性，验证了文章方法的有效性。