基于PSO-RF的GNSS-IR土壤湿度反演方法研究

孙 波，张 弛，尹世超，许 浩，张伟杰

(1.山东农业大学 信息科学与工程学院，山东 泰安 2710182.中华人民共和国科学技术部 国家遥感中心，北京 100036)

0 引言

土壤湿度是农田环境的一个重要指标，是影响农作物正常生长的重要因素[1]。因此，农田土壤湿度的大范围、实时、精确地获取对于指导农田精准灌溉、提高现代农业的智能化水平具有重要的研究意义。

基于全球导航卫星系统干涉测量(Global Navigation Satellite System Interferometry and Reflectometry，GNSS-IR)技术的土壤湿度探测方法是一种新兴的被动微波遥感方式。与目前已有的探测方式相比，弥补了传统烘干称重法在实时性及对农田的破坏性方面的弊端，同时解决了传统微波遥感方式造价高、时空分辨率低的问题，近年来已成为微波遥感技术研究的热点[2]。

GNSS-IR技术从探测模式上又称为GNSS单天线技术，起源于欧美。2008年，美国科罗拉多大学Larson团队[3-6]首先提出利用已有的GNSS普通信号接收机在接收导航卫星直射信号的同时，也能够接收地面的散射及反射信号，实测结果验证了土壤湿度与接收的直反射信号产生的干涉信噪比(Signal to Noise Ratio，SNR)的振幅和相位有关。在此基础上，法国图卢兹三大的Roussel团队[7-8]分析了全球定位系统(Global Positioning System，GPS)和格洛纳斯系统(Global Navigation Satellite System，GLONASS)在不同卫星高度角条件下的SNR数据，证明了从低高度角2°～30°的SNR数据中提取的特征参量与土壤湿度相关性较高。国内学者也在相关领域展开了研究，桂林理工大学任超团队[9]将小波变换应用到直反射信号分离的过程中，提高了SNR特征参量的提取精度，进而改善了土壤湿度的反演精度。

综上所述，从国内外研究进展看，GNSS-IR技术已被证明可以有效地进行土壤湿度的反演，但大部分研究只是验证了土壤湿度与SNR特征参量的相关性，缺乏理论模型及经验模型，且反演精度较低；此外，前期的研究大多围绕GPS的应用展开，而随着我国北斗系统的组网完成，基于北斗系统的相关研究将是今后研究的热点。因此，本文将随机森林(Random Forest，RF)的机器学习方法引入到GNSS-IR土壤湿度的反演过程中，利用机器学习的黑箱特点来克服土壤粗糙度及系统噪声对反演精度的影响，进一步引入粒子群优化(Particle Swarm Optimization，PSO)算法解决随机森林模型的参数优选问题，并展开北斗系统的相关实验，验证了所提方法可以有效地提高反演精度。

1 GNSS-IR土壤湿度反演原理

在地基单天线模式下，信号接收机可以同时接收导航卫星的直反射信号，由于地基接收天线高度较低，直反射信号可以看成衰减不同的同频电磁波[10]，接收时产生的干涉信号会被接收机以SNR的形式记录下来，具体表现为随高度角变化的一定趋势上的振荡现象，如图1所示。

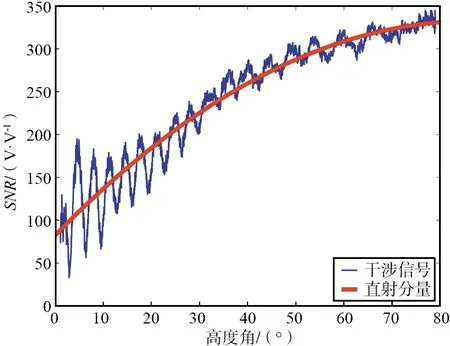
图1 上升段SNR波形 Fig.1 Waveform of the ascending SNR

SNR的数学模型可表示为[11]：

(1)

式中，Ad为收机接收的卫星直射信号幅度；Am为地表的反射信号幅度；ψ为Ad,Am由路径差引起的相位差。由于土壤湿度等地表信息仅影响SNR的反射分量，通过多项式拟合可以把与反演无关的直射分量去除，仅保留多径反射振荡分量，如图2所示。

图2 SNRm的波形Fig.2 Waveform of the SNRm

进一步利用谱分析法可以得到振荡频率f，用正弦信号对该分量进行逼近拟合，则多径反射信号SNRm可以表示为：

SNRm=Amcos(4πHλ-1sinθ+φ)，

(2)

式中，λ为GNSS卫星信号的波长；θ为卫星的高度角；H为接收机天线的等效高度。通过最小二乘拟合可以得到SNRm的干涉特征参量：振荡幅度Am和振荡相位φ。文献[3-8]已证明上述干涉特征参量与土壤湿度存在相关性，本文选取相关性较好的SNRm的振荡频率作为反演的特征观测量。

2 PSO-RF的土壤湿度反演模型

土壤湿度反演从方法上属于回归的范畴，文献[3-9]采用特征观测量的一元回归方法反演得到的土壤湿度在精度方面并不理想，仅利用单一频点GNSS干涉信号反演土壤湿度，忽视了不同频点信号间的差异性及潜在的更丰富的观测信息。随着人工智能的兴起，越来越多的学者开始尝试将机器学习方法引入到反演过程中，取得了不错的效果[12-13]。本文采用非线性RF回归方法，融合北斗B1,B2双频段的振荡频率观测量进行土壤湿度的反演研究。

RF算法是一种新兴的、高度灵活的基于决策树的机器学习算法。本质上属于集成学习的一个重要分支，采用非参数计算，以随机的方式生成若干弱决策树，并通过集成所有决策树的预测结果进行预测，既可以解决分类问题也可以用于回归分析，应用领域广泛[14]。该算法的随机主要体现在决策树生成的2方面：① 随机选取子样本；② 随机选取输入参数，该方式有效降低了决策树之间的相关性，使RF算法具有良好的鲁棒性和预测精度。土壤湿度反演本质上为回归问题，适用于RF算法进行处理，输出结果为每棵决策树得到的土壤湿度均值。

实验证明，超参数中的决策树个数n_estimators、决策树最大深度max_depth以及最大叶子节点数max_leaf_nodes对RF的性能影响较大，在参数的选取上，既要提高反演的准确性还需要考虑算法的运行效率。本文引入了PSO算法对RF回归模型的上述3个超参数进行自动寻找最优解，避免了人为调参的随意性。

PSO算法是一种全局的随机搜索算法，其基本思想来源于鸟群在迁徙过程中的群聚捕食行为[15]。该算法采用种群中个体的适应度评估个体优劣，在 RF算法中首先对超参数n_estimators、max_depth以及max_leaf_nodes随机初始化一群粒子，计算相应的适应度值，并通过不断更新粒子的速度和位置来达到最佳的适应度值，从而得到最佳RF模型的超参数n_estimators、max_depth以及max_leaf_nodes，进而提高RF模型的收敛速度及预测性能。

基于PSO-RF的土壤湿度反演模型如图3所示。

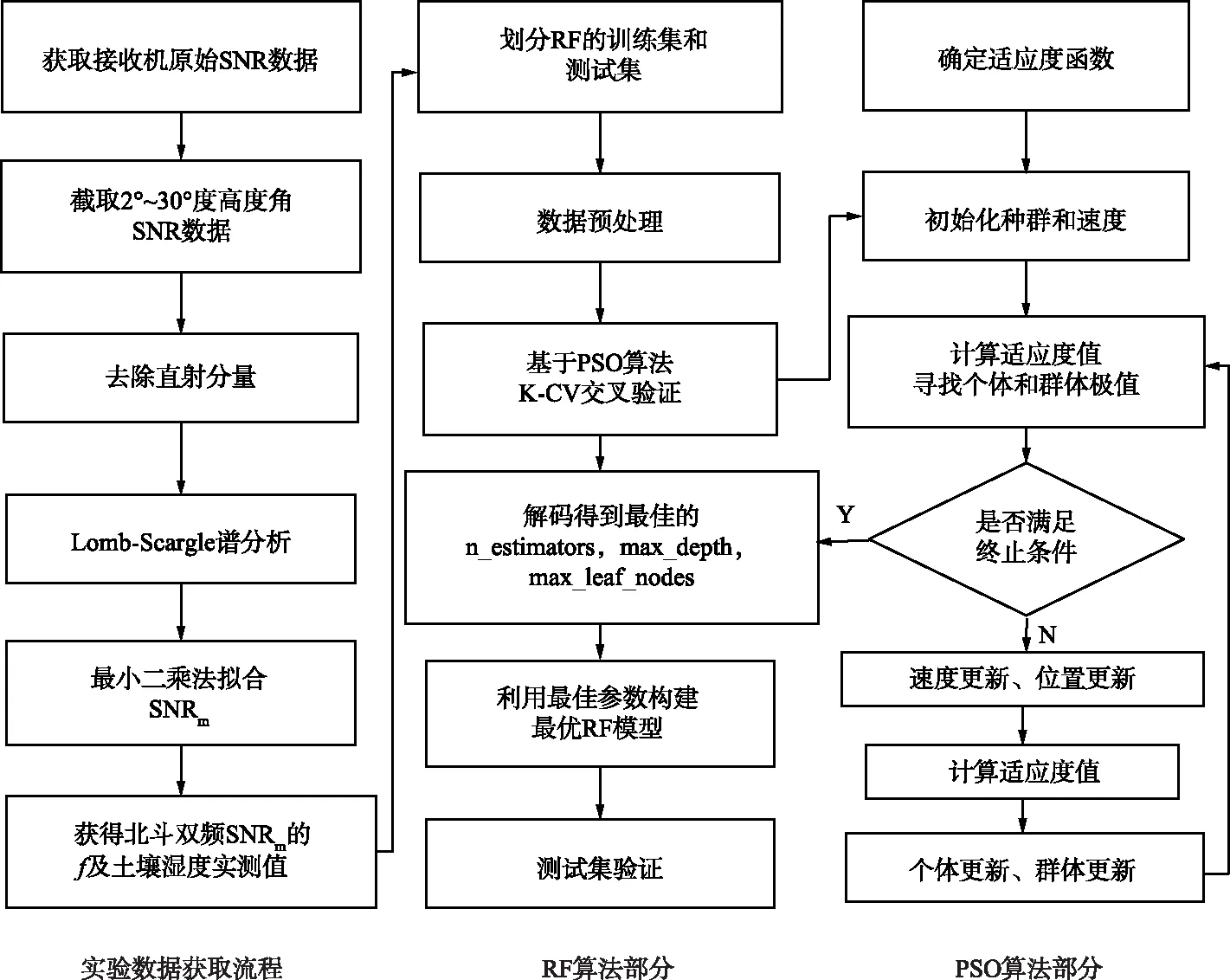
图3 PSO-RF模型Fig.3 PSO-RF model

3 模型验证

3.1 GNSS-IR数据采集

为了对所提方法进行验证，2018年9月10—11月9日在通州区北京市农林科学院蔬菜研究中心( 116°41′23.19″E，39°41′50.33″N)开展了61 天的探测实验。场地四周空旷无遮蔽，实验期间为秋冬季，地表可视为裸土，现场如图4所示。接收机天线架设高度为 3 m，采样频率为 1 Hz，同时采集北斗系统B1,B2频段以及GPS系统L1,L2,L5频段的直、反射信号。根据文献[7]，GNSS-R可以探测0～50 mm的地表土壤湿度，为了进行同比验证，在第一菲涅尔反射区内安装3个深度分别为20,40，50 mm的高精度传感器采集土壤湿度，取其平均值作为日土壤湿度真值。架设自动气象站采集同期气象数据，采样间隔60 s。

图4 实验场地信息Fig.4 Experimental site information

3.2 数据处理及结果分析

3.2.1 样本数据的选取

按照图3的流程对北斗系统接收数据进行处理，得到61组北斗B1，B2的振荡频率观测量，然后与土壤湿度真值按照2∶1的间隔比例划分成训练集与测试集，分别进行PSO-RF的回归反演及传统回归方法的反演。综合考虑实验场地的经纬度及天线架设位置，以及方位角和高度角的限制，满足以上条件的仅有PRN9，PRN10和PRN13三颗卫星。

3.2.2 PSO-RF模型训练

将训练集的北斗B1，B2的振荡频率观测量及土壤湿度真值分别作为PSO-RF模型的输入输出进行训练。为了提高反演模型的精度及泛化能力，对RF模型的超参数n_estimators，max_depth以及max_leaf_nodes 进行优选是关键。根据文献[16]，PSO 的相关设置如下:最大进化代数为200，种群数量为20，学习因子C1，C2均为2，交叉验证次数V= 5。通过PSO搜索算法进行寻优，当粒子的适应度趋于稳定或迭代次数达到最大时，终止迭代循环，确定最终寻优结果。

3.2.3 结果分析

将最优参数n_estimators，max_depth，max_leaf_nodes代入RF 模型，分别将北斗PRN9，PRN10和PRN13 卫星的测试集数据输入PSO-RF模型进行预测反演，所得结果如图5 所示。

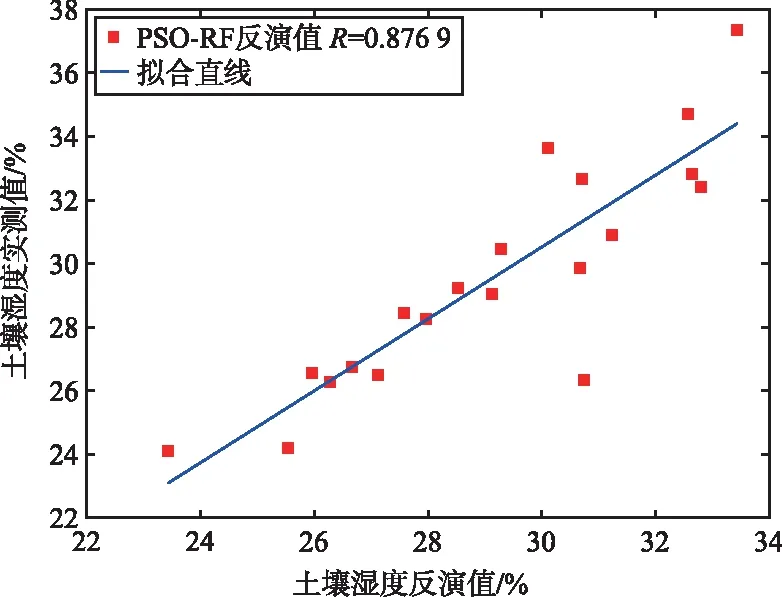
(a) PRN9反演结果

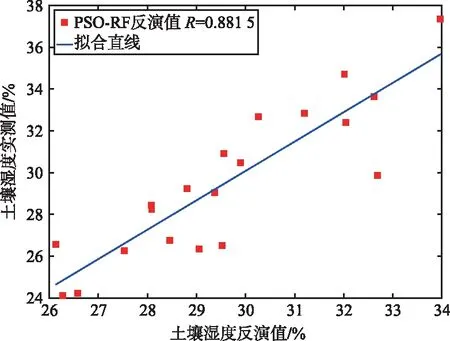
(b) PRN10反演结果

(c) PRN13反演结果图5 不同卫星PSO-RF模型反演结果Fig.5 PSO-RF model inversion results of different satellites

由图5可以看出，PRN9，PRN10，PRN13三颗星的土壤湿度反演值与实测值的线性相关系数R分别达到了0.876 9，0.881 5，0.831 4，反演结果接近实测值，证明了PSO-RF方法也可以有效地应用到土壤湿度的探测领域。

3颗星的PSO-RF方法与利用B1，B2频段SNR振荡频率的传统回归方法的反演结果如图6所示。

(a) PRN9反演结果对比

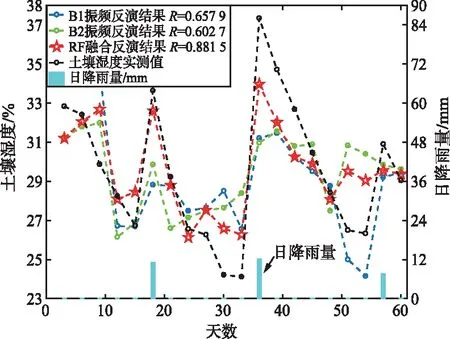
(b) PRN10反演结果对比

(c) PRN13反演结果对比图6 不同反演模型结果对比Fig.6 Comparison of results of different inversion models

由图6可以看出，PSO-RF方法反演值与实测值具有更明显的相关性，反演结果反映出了土壤湿度变化的趋势和降雨过程。相比于传统回归方法的反演结果，相关系数R分别提高了32.88%，48.1%，说明PSO-RF优化模型较传统回归模型性能有明显提升。

为了进一步验证各反演模型的有效性，本文还通过均方根误差(Root Mean Square Error，RMSE)对上述3颗星的反演结果进行了误差分析，如表1所示。

表1 反演误差对比Tab.1 Inversion error comparison

由表1可以看出，PSO-RF方法反演结果的RMSE最小，与北斗B1，B2的传统回归方法相比，RMSE分别降低了18.93%，62.98%，反演精度得到了明显的提升。

4 结束语

根据GNSS-IR的探测原理及数据分析结果，构建了基于PSO-RF的土壤湿度反演的半经验模型，并开展了实验对该模型进行了验证测试。得到如下结论：① 在北斗系统低高度角条件下(2°～30°)，利用PSO-RF方法得到的测试集反演值与土壤湿度真值相关性较好，相关系数均达到了0.8以上，均方根误差在2%以下，说明该方法可以较好地实现对固定区域土壤湿度的连续监测。② 与利用振荡频率的传统回归模型相比，PSO-RF模型的反演结果在相关系数及误差方面均有较明显的改善，说明利用PSO-RF方法融合了北斗B1，B2的双频观测量，综合利用了不同频段信息间的差异性，从而在反演的精度方面得到有效的提升。③ 北斗组网目前已经完成，围绕北斗系统的反演模型及实验验证的相关工作将是未来的趋势和研究重点。

由于本次实验处于秋冬季，农田地表近似为裸土，且地形平坦，没有考虑土壤粗糙度的影响。因此，深入研究具体农作物覆盖及地表粗糙度对GNSS接收机信噪比的影响是下一步的主要工作。