反激变换器的输出反馈模型预测控制仿真研究

管雪梅 吴马超 魏艳秀 王子龙(东北林业大学机电工程学院 黑龙江 哈尔滨 150040)

0 引 言

反激变换器具有电路简单、成本低、输入与输出电压电气隔离等优点，广泛用作中小功率电气设备的供电电源。但变换器因开关管周期性的切换工作模式而表现出非线性，且负载不确定性和线路振荡严重影响闭环控制器的稳定性，当变换器处于不同静态工作点时，一般线性模型难以解决输出电压稳定性的问题[1-2]。

针对这些问题，一些研究者提出了不同的非线性控制方法，比如自适应控制、模糊控制、滑膜控制和模型预测控制[3-6]。在文献[7]中，设计输出电压外环反馈和变压器激磁电流内环反馈，使得滑膜控制器的最终控制律中存在输出电压误差的积分，即使输入电压和负载阻抗发生变化，输出电压在稳态下仍保持零稳态误差。文献[8]针对负载变化较大而引起极点偏移的问题，采用闭环双模降阶预测控制算法，其仿真结果证明在电路负载变化范围较大时依然能较快响应并保持良好的动态过程。文献[9]设计了模型预测电压控制方法，实时监测输出电压、变压器一次侧电流和次级侧电流，优化下一步控制，提高了输出电压的快速响应能力和稳健性。而文献[10]去除电流控制环路，提出直接电压控制的模型预测方法。同时，增加一个卡尔曼滤波器来估测Boost变换器的状态，提供输出电压无偏移跟踪，很好地解决了随时间变化和未知的负载，保证闭环控制器的快速瞬态响应和高度的鲁棒性。

基于以上理论研究，模型预测算法依靠显示处理优化能力很好地解决了变换器的动态性能问题。但对于Flyback型DC-DC变换器，其变压器一次侧电流难以检测。因此，在基于双线性模型的状态反馈基础上[11-12]，增加一个Luenberger-type型观测器，设计输出端电容器电压调节的输出反馈模型预测方案。其观测器增益在保证状态估计误差全局收敛的情况下，外加PI控制环消除电容器电压偏移误差。仿真结果表明在输入电压变化或负载变化的情况下均能满足控制要求。

1 双线性模型

图1为实际Flyback变换器分析电路图，其中：ig(t)表示电压源电流；vg(t)表示电压源电压；vL表示电感电压；C表示电容；v(t)表示输出电压；iC(t)表示流经电容电流。考虑现实情况下变压器为非理想的，理论分析时采用理想变压器并联一个激磁电感L代替实际变压器，此时激磁电感的内阻RL不为零。开关导通状态与开关截止状态下的电路图如图2所示，其中：R为负载电阻；RON是开关管Q1的导通电阻；vD为二极管导通电压。

图1 Flyback变换器分析电路图

在一个开关周期的(0,dTs)内，即主开关Q1导通，二极管D1截止时，状态方程为：

(1)

在一个开关周期的dTs时刻，主开关Q1关闭，此(dTs,Ts)时间段内，状态方程为：

(2)

式(1)和式(2)中，有i(t)=ig(t)=iL(t)，v(t)=vC(t)，则可以描述为：

(1) 开关导通，二极管截止状态:

(3)

(2) 开关截止，二极管导通状态:

(4)

其中：

结合式(3)和式(4)可以得到一个开关周期的平均状态模型：

(u(t)Bc1+(1-u(t))Bc2)v

(5)

式中：u(t)=D∈[DminDmax]⊆[0 1]，常数Dmin和Dmax是占空比D的上下界包络线。

式(5)展开得：

((Bc1-Bc2)v)u(t)+Ac2x(t)+Bc2v

(6)

令：

Gc=Ac1-Ac2Bc=(Bc1-Bc2)v

则式(6)变为：

(7)

设采样周期(时间)为h，将连续时间系统式(7)转化为离散时间系统：

x(k+1)=A2(k)+(B+G(k))u(k)+B2v

(8)

此时，A2=hAc2+I,B=hBc,G=hGc,B2=hBc2。

2 状态反馈模型预测控制器设计

基于第1节离散时间模型，给定输出电压参考值r，控制目标是使输出端电容器电压尽可能地接近参考值电压，即：

(9)

则在系统稳定条件下，离散时间系统可以表示为：

x0=A2x0+(B+Gx0)u0+B2v

(10)

(11)

(12)

u0∈[Dmin,Dmax]

(13)

令：

则式(11)展开为：

b21vg+b22vD

(14)

b23vg+b24vD

(15)

由式(15)可以给出输入u(k)在稳定状态下u0(r)：

(16)

将式(16)代入式(14)整理得：

(17)

式中：α2=(1-a21)g3+a23g1；

α1(r)=(1-a21)(b2+g4r)+a23b1+

g1((1-a24)r-b23vg-b24vD)+a23g2r+

g3(a22r+b21vg+b22vD)

α0(r)=-b1((1-a24)r-b23vg-b24vD)-

g2r((1-a24)r-b23vg-b24vD)-

(b2+g4r)(a22r+b21vg+b22vD)

式(16)可解得：

(18)

因此，x(k)的稳定状态为：

(19)

由式(17)可知，在u0(r)∈[Dmin,Dmax]范围内，保证使电容器电压尽可能地接近参考值r，使得电感器电流在稳定状态下存在着两个有效的可能解。

基于稳定状态x0(r)，定义状态反馈追踪误差ex(k)=x(k)-x0(r)，则：

ex(k+1)=A2x(k)+(B+Gx(k))u(k)+

B2v-x0(r)=

A2x(k)+(B+Gx(k))u(k)-

f(x(k),u(k)) ∀k

(20)

根据式(20)得到优化约束函数，即：

(21)

为了求解k时刻控制量，令：

∂Vc(ex(k+1))/∂u(k)=0

(22)

可得：

uuc(x(k))=-(TT(x(k))PcT(x(k)))-1×

TT(x(k))Pc(A2x(k)+B2v-x0(r))

(23)

式中：T表示关于x的函数表达式。

则在任意时刻控制律u(k)可以表示为：

(24)

其中：

Ac=DminhAc1+(1-Dmin)hAc2+I

Ac=DmaxhAc1+(1-Dmax)hAc2+I

则状态反馈模型预测闭环控制系统的控制律是全局指数稳定。证明如下：

选择一个李雅普诺夫函数：

(25)

则Vc(ex(k+1))=Vc(f(x(k),k(x(k)))≤

Vc(f(x(k),u0(r)))=

(26)

式中：Ac(u0(r))=u0(r)hAc1+(1-u0(r))hAc2+I。

作差分：

ΔVc(ex(k))=Vc(ex(k+1))-Vc(ex(k))≤

(27)

式(27)中，对任意k和任意ex(0)≠0，只要满足：

(28)

则式(29)成立，意味着控制律式(24)是全局指数稳定。

ΔV(ex(k))<0,∀k,∀ex(0)≠0

(29)

左右两边乘以矩阵：

则式(28)等价于：

(30)

与假设1的约束条件是一致的。

3 输出反馈模型预测控制器设计

结合上节状态反馈模型预测式(24)，通过添加一个Luenburger-type观测器，提出一种基于电容器电压管理的无偏移输出反馈模型预测控制策略。图3为输出反馈模型预测控制原理图，其中yref(k)表示参考电压。

对于式(8)，电容器电压等价于输出电压y(k)，因此，输出电压y(k)可以表示为：

y(k)=Cox(k)

(31)

式中：Co=[0,1]。

3.1 Luenberger-type观测器设计

为了预测状态x(k)，选取一个Luenberger-type观测器：

(32)

(33)

则：

-(TT(x(k))PcT(x(k)))-1×

TT(x(k))Pc(A2x(k)+B2v-x0(r))

定义估测追踪误差：

(34)

满足：

eo(k+1)=(A2+u(k)G-LoCo)eo(k)=

(35)

由于时变项u(k)∈[Dmin,Dmax]，对于任意k时刻，eo(k+1)是上下有界的。因此只要找到增益矩阵Lo，可以使式(35)稳定。

证明如下：

定义李雅普诺夫函数：

(36)

作差分：

ΔVo(eo(k))=Vo(eo(k+1))-Vo(eo(k))=

(37)

如果式(38)成立：

(38)

则：

(39)

左右两边同乘矩阵：

则式(38)等价于：

(40)

将其改写成：

(41)

式中：Am1=A2+DminG-LoCo；Am2=A2+DmaxG-LoCo。

即式(41)等价于假设2的约束矩阵。因此，对于ΔVo(eo(k))<0，且Vo(eo(k))是二次型，证明状态估测动态误差是全局指数稳定。

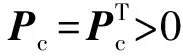
3.2 闭环稳定性分析

3.1节由假设2确保观测动态误差的稳定性，分析在具有观测误差的情况下，输出反馈模型预测控制律的闭环稳定性。定义观测器追踪误差：

(42)

则有：

(43)

式(43)中如果没有补偿项LoCoeo(k)，则是由状态反馈控制器推导的闭环系统。因此式(43)的动态性可以理解为稳定系统加上一个干扰项LoCoeo(k)。对于闭环系统，针对干扰项LoCoeo(k)，应用输入到状态稳定概念，分析式(43)的稳定性。

引理1如果假设1的线性矩阵不等式成立，则闭环观测器追踪动态误差是输入到状态稳定，即：

(44)

式中：λmin(Q)表示取特征值最小值；ζ表示取标准差的无穷小值(全局最小值)。

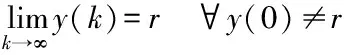
证明：由式(36)定义的Vo(eo(k))，则闭环系统：

(45)

式中：σ为待定常数。

作差分：

根据假设2和引理1，可得：

(46)

因此：

(47)

根据式(47)的特性，可知输出反馈控制器方案不仅确保电容器电压全局收敛，而且确保存在输入约束条件下的电感电流全局收敛。

3.3 外环PI控制器

由于所提出输出反馈模型预测控制方法依赖转换器参数，在实际工况下，因为存在着控制模型失配，电容器电压在稳定状态下可能发生偏移误差。为了消除偏移误差，外环引入PI控制进行补偿。假设内环控制系统非常快，即内环的传递函数为1。则可假设：

y(k)≈c(k)

(48)

c(k)为外环PI控制器输出：

其中：r为y(k)参考值；h为采样周期。

可得：

(49)

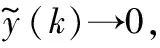
4 仿真验证

为了验证本文所设计控制器的有效性，利用MATLAB 2011b/Simulink进行如下仿真实验。设计输出功率为72 W、输出电压为36 V的反激变换器，对PID控制进行仿真，图4为PID输出电压波形，可以看出：PID控制调节时间为4×10-3s，超调量达到36%，稳态误差为±5.5%。控制效果不能满足高精度的要求。

图4 PID控制时输出电压波形

给出Flyback型DC-DC转换器的参数如下：L=140 uH，RL=0.01 Ω，C=470 uF，vg=110 V，vD=0.67 V，R=18 Ω，RON=0.08 Ω，n=1/3。采样时间h=0.1 ms。最小和最大占空比设定为Dmin=0.2和Dmax=0.95，以此最大间距确保存在Pc满足假设1中的不等式。则假设1中的Ac(Dmin)和Ac(Dmax)可以确定为：

基于矩阵Ac(Dmin)和Ac(Dmax)，确定矩阵Pc满足假设1中不等式：

同样地，确定u=0.98，假设2中线性不等式的Po和Yo可以给出：

则观测器增益矩阵Lo可以确定：

对于外环控制，PI控制器的参数系数为：

KP=40KI=0.5

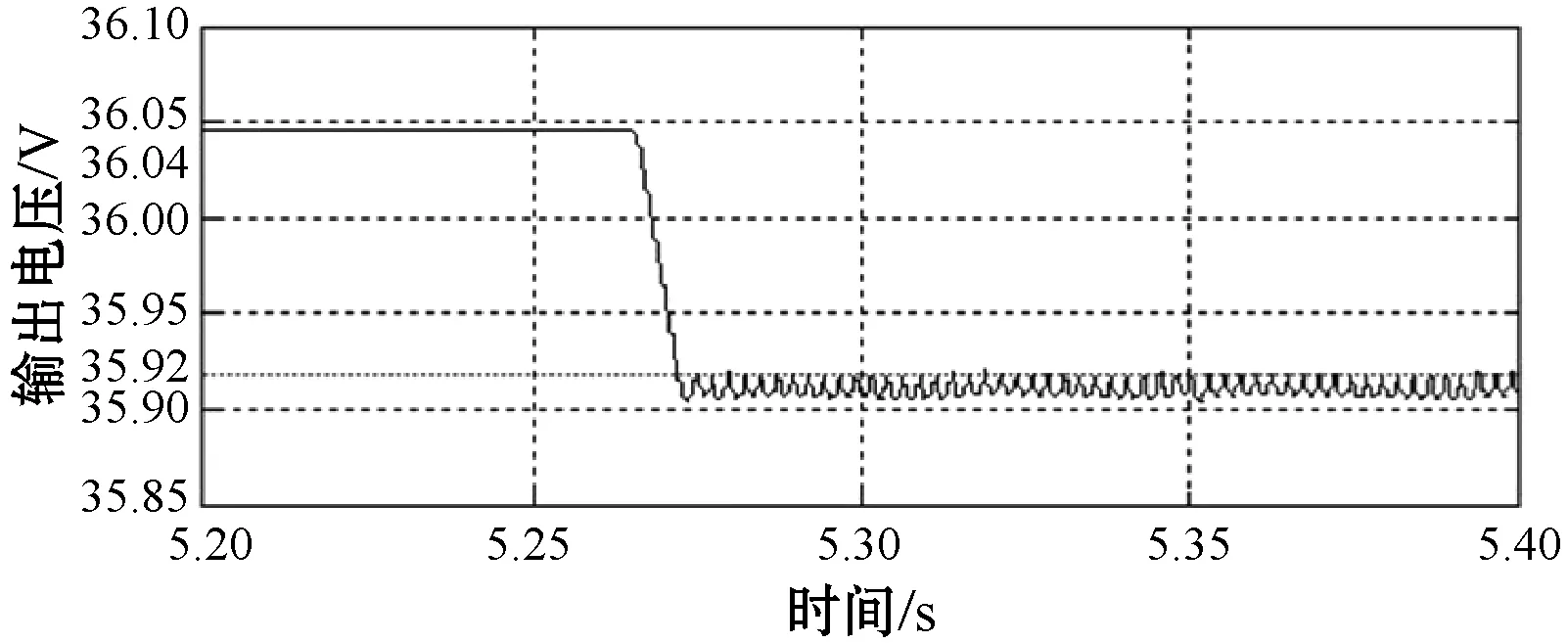
仿真结果如图5-图9所示。

(a) 输出电压

图6 误差对比

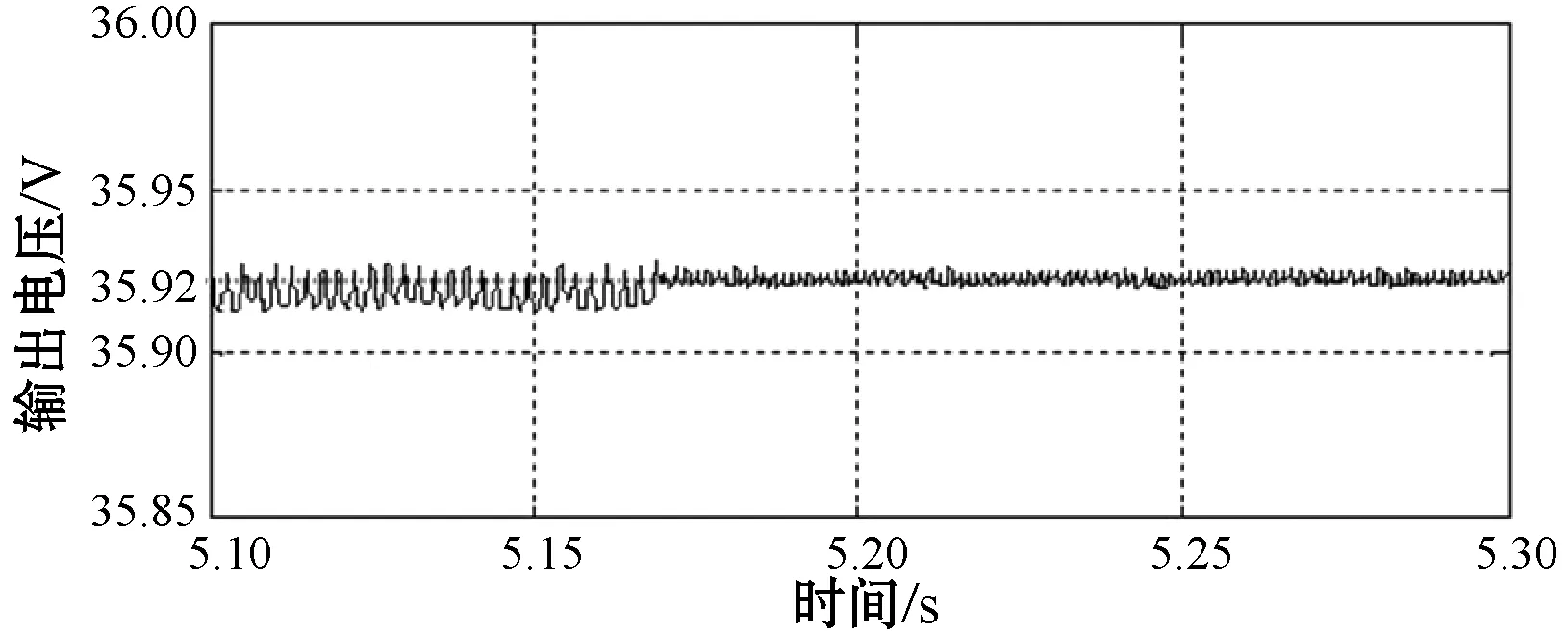
(a) 输出电压

从图5可以看出：在输入交流电压为220 V保持不变的状况下，系统空载时稳定输出电压为36.04 V，输出特性良好。当由空载瞬间加到满载时，稳定输出电压变为35.92 V，稳定输出电流为2 A，此时动态响应时间为0.01 s，系统稳定后的稳态误差为0.22%，控制精度高。图6给出PID控制和Flyback型DC-DC控制下的输出电压对比，可以明显看出改进系统具有良好的抗干扰性和稳定性。图7给出系统稳定后误差电压变化，可以看出，误差电压一直处于0.08～0.09 V范围之内变化，误差电压在有限时间内收敛。图8给出了电源输入电压保持不变，负载由满载迅速卸到半载时的动态变化，可以看到在很短的时间内，输出电压没有出现尖峰波形，过渡过程平稳，且电压变化控制在0.01 V以内，表明控制系统具有良好的适应性和稳定性。图9显示，保持负载为满载不变状况下，输入电压上下浮动时，输出基本稳定不变，没有明显尖峰，表明系统具有很强的抗干扰性。

5 结 语

针对反激变换器的输出电压稳定性问题，提出基于Flyback变换器研究一种输出反馈模型预测控制器。对控制器进行了闭环稳定性分析，并在MATLAB 2011b/Simulink环境下进行了仿真。理论分析和仿真结果表明：被控系统具有良好的响应曲线，实现了高精度、强鲁棒性、快速性的性能，避免了系统过程中出现的高超调、震荡大、响应慢、稳定性差等缺点，说明了输出反馈模型预测控制策略在性能上增强了系统的抗干扰能力，改善了控制性能。