螺旋锥齿轮三维齿面接触分析研究 *

李敬财 霍津海 满 佳 王 鹏

(①天津职业技术师范大学机械工程学院，天津 300222； ②天津精诚机床股份有限公司，天津 300400)

螺旋锥齿轮作为空间相交轴(弧齿锥齿轮)和空间交错轴(准双曲面齿轮)的动力传动的核心部件，广泛应用于汽车、航空航天、船舶和电动工具等行业的动力传动中。在实际应用中通常是以齿面接触区作为评价齿面啮合质量的关键手段，而影响齿面接触区的主要是与齿轮的修形量以及所对应加工调整参数有很大的关系，而作为加工前的接触质量预报，通常是根据基于加工调整参数的齿面接触分析实现。20世纪60年代早期，提出采用齿面接触分析(TCA)技术对弧齿锥齿轮及准双曲面齿轮副的接触特性及运行质量进行理论分析。最初采用TCA技术作为齿面接触分析技术的是Litvin F L等[1]以及Baxter M L[2]。美国格里森公司(Gleason Works)、德国克林贝格集团( Klingelnberg)的科学家和工程师们对TCA技术的发展做出了很大的贡献[3]，并开发出商用软件[4-6]。由于采用TCA程序可以大大减少螺旋锥齿轮设计和制造过程中的反复进行试算、试切过程所需的时间，目前广泛用于齿轮工业中。目前齿面接触分析计算的齿面接触区算法都是基于齿面诱导曲率来计算，其计算结果是二维的[7-8]，不具有直观性，为获得更具直观的三维齿面接触区，作者提出采用数值法求解齿面接触区。

1 螺旋锥齿轮齿面数学模型的建立

螺旋锥齿轮齿面是由加工其刀具表面包络而成，具有直线刃的刀盘可以认为是个锥面。切削大轮和小轮刀具的锥面在坐标系Sc(与切削刀具固连)中的位置矢量、单位法矢量和单位切矢量为

(1)

其中：(ui,θi)是锥面参数，i=1表示切削小轮刀具，i=2 表示切削大轮刀具。

基于自由曲面加工的 CNC螺旋锥齿轮加工设备和传统采用摇台机构的螺旋锥齿轮加工设备都用于螺旋锥齿轮的加工。通常齿面数学模型在与齿轮i固连的坐标系Si下表示为(i=1,2)。

(2)

式中：φi是被加工齿轮的转角;fi=0为啮合方程(i=1,2)。

2 齿面接触迹线求解

修形后螺旋锥齿轮理论啮合齿面为点φ2接触啮合齿面，在啮合过程中接触点的连线称为接触迹线。图1为啮合齿面Σ1和Σ2在安装坐标系下示意图，用于模拟啮合过程的坐标系Sf与机座固连。齿面Σ1及Σ2在M点啮合,T是在点M处的切平面。φ1和φ2分别是小轮和大轮的角位移，小轮和大轮在点M处啮合。小轮和大轮在Sf坐标下的位置矢量和单位法矢量方程为

(3)

(4)

通常情况下，用于齿面接触分析TCA计算的方程组是基于在接触点出位置矢量和法矢量相等条件下建立的(图1)，在坐标系Sf下其数学表达式为[9]:

(5)

(6)

f1(u1,θ1,φ1)=0

(7)

f2(u2,θ2,φ2)=0

(8)

当φ1为输入参数，方程(5)～(8)组成的方程组是由具有7个变量的非线性方程组成。其中u1、θ1、φ1、φ1、u2、θ2、φ2、φ2为由方程(5)～(8)组成的方程组的未知数。

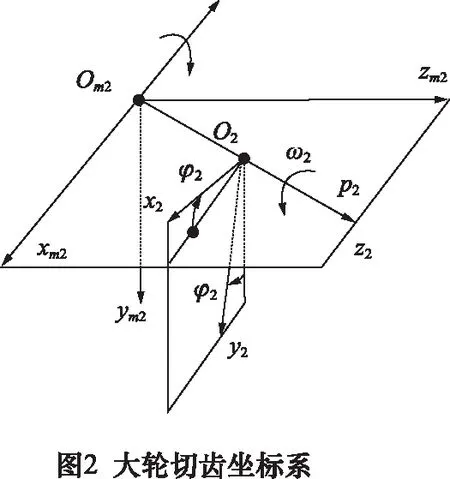
为了减少迭代方程的数目和提高迭代过程的收敛性，方程(6)～(8)可以分别用u1、u2、φ1, 显性表达出来。图2、图3分别为大轮和小轮的切齿坐标系，Sm1和Sm2分别为加工大轮和小轮的机床坐标系，坐标系S1、S2分别与小轮和大轮固连。方程(7) 、(8) 可以用u1、u2表达，在此仅给出结果:

(9)

(10)

其中：

方程(6)可以用φ1,φ2显示表达。

(11)

(12)

其中：p1、p2分别为与小轮和大轮轴线共线的单位矢量 (图4 )。

由式 (9)、(10)可知，u1、u2可被显示表达为

u1=u1(θ1,φ1)

(13)

u2=u2(θ2,φ2)

(14)

由公式(11) ～(14) ，φ1、φ2显示表达为

φ1=φ1(θ1,φ1,θ2,φ2)

(15)

φ2=φ2(θ1,φ1,θ2,φ2)

(16)

因此，用于TCA迭代的方程组 (5) ～ (8)可以减少为由方程组 (13)～(16)

(17)

由公式(17)进行TCA计算的方程组仅包括3个非线性方程。当给定参数φ1时，用公式(17)计算出瞬时啮合齿面点坐标值，当φ1变化时可求得一系列齿面啮合坐标点，求得齿面接触迹线。

3 数值法求解瞬时接触区域

尽管螺旋锥齿轮是理论点啮合，但是其在轻载下其齿面会有轻微的塑性变形，当齿面接触时会在接触点周围扩展一个椭圆区域，在接触点法矢量方向，当间隙小于δ时，便认为这两个齿面是在瞬时的接触区域(图5)，通常δ=0.006 35 mm[10]。以往算法是通过计算两个齿面诱导曲率获得齿面瞬时接触椭圆，但是仅能得到二维的接触椭圆参数以及二维齿面接触区。本文采用数值法求解齿面瞬时接触区域，可获得三维齿面接触椭圆，从而获得三维齿面接触区，使得接触区更加直观。

3.1 局部坐标系的建立

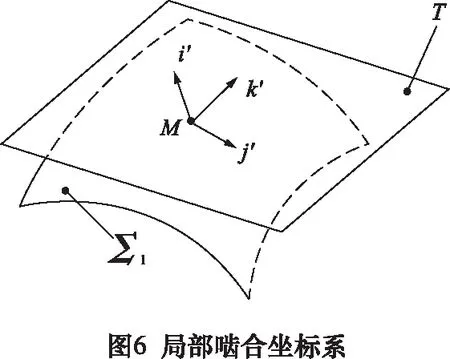
螺旋锥齿轮齿面Σ1、Σ2在点M接触，局部坐标系SM(M;i′,j′,k′) 原点是在当前接触点处，j′、k′在切平面T(图6)，其中

(18)

(19)

k′=i′×j′

(20)

在局部坐标系SM下，Σ1、Σ2位置矢量可由下式表示

(21)

其中：MMf为由Sf到SM变换矩阵。

3.2 数值法求解瞬时接触边界

瞬时接触边界可以认为是由一系列沿着接触点处法矢量方向间隙值为δ的点组成。其详细描述如下。

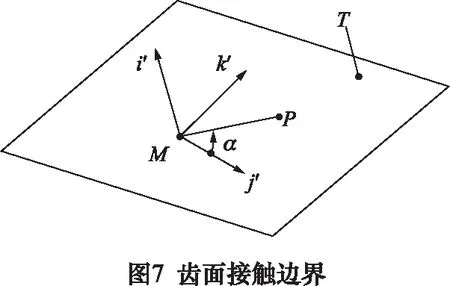
在图7中，Mp为切平面上的一个线段，在SM坐标系下，端点p可以表示为：

(22)

如图8,p(1)、p(2)为由点p沿着i′分别与小轮和大轮齿面交点，这两点在SM坐标系下可表示为：

(23)

(24)

沿着i′方向，p(1)、p(2)两点距离为δ(图 5), 距离公式可由下式表达:

(25)

由式(23)、(24) 及(25),用于求解瞬时接触椭圆的方程组为

(26)

其中：(θ1(α),φ1(α),θ2(α),φ2(α),Mp(α))为需要求解未知数，α(α∈[0,2π))和δ为已知值。方程组(13)为非线性方程组，改进的Powell 混合算法用

于求解该方程组[11-12]。在由式(26)求解出未知数(θ1,φ1,θ2,φ2,Mp)基础上,由式(2)求解出在齿面Σ1、Σ2的瞬时接触边界，由式(25)可以求解出瞬时接触边界在啮合点出的切平面T上的投影，该投影类似椭圆。

3.3 瞬时接触区域的方向求解

如上所述，瞬时接触区域类似椭圆，由式(26)可以求解出4个解Mpi(αi)(i=1,...,4)，这4个解的关系为：

Dmax≈Mp1(α1)+Mp2(α2)

(27)

Dmin≈Mp3(α3)+Mp4(α4)

(28)

其中：Dmax(Dmin) 为瞬时接触椭圆的长轴(短轴)。

在切平面T上对应的瞬时接触椭圆的方向可由αi(i=1,...,4)表示(图9)。 瞬时接触椭圆求解流程如图8所示。

表1 齿坯参数

4 算例

本算例中给出的齿轮为9×35准双曲面齿轮。表1为齿坯参数，表2为加工调整参数，根据表1、表2给定参数通过公式17求解的一个瞬时点对应的参数值(见表3)，根据公式(26)、公式(30)、公式(31)求解该给定啮合点处接触椭圆在切平面上的接触边界(图9)，由计算结果可知实际上接触边界不是严格意义上的椭圆，其形状类似椭圆，图10为该瞬时接触椭圆在大轮三维齿面上计算结果。图11为计算一系列瞬时接触椭圆形成的三维齿面接触区。

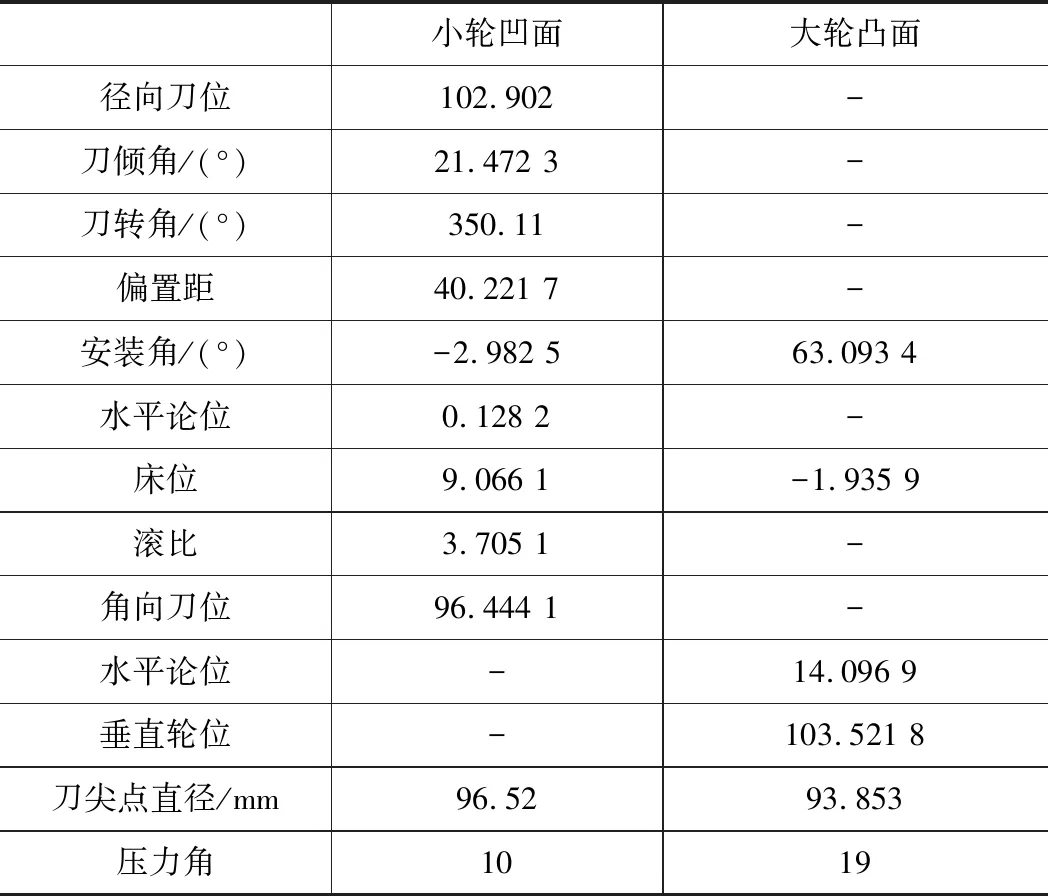
表2 加工调整参数

表3 啮合点处瞬时接触椭圆

值得说明的是，由于加工不可避免产生齿面误差，无法通过试切法滚检得到接触区与理论计算结果(图10、图11)对比验证该算法的正确性。但是通过将新算法得到的三维齿面接触区参数转化二维齿面接触区并与美国格里森公式的商业软件(CAGE)齿面接触分析计算结果对比，结果表明二者总体趋势是一致的。

5 结语

以往采用啮合齿面诱导曲率方式求解瞬时接触区是在假设该瞬时接触边界符合理论椭圆公式基础上求得的，可获得二维齿面接触区；本文采用数值算法求解了瞬时齿面接触区，计算结果表明在轻载下齿面瞬时接触边界为类似椭圆形状的三维空间曲线，采用数值法可获得轻载下螺旋锥齿轮的三维齿面接触区。