结合台风全路径模拟的宁波地区台风极值风速估计

梁陆军 王炎铭 李 强 毛江鸿 郏鸿韬

1. 浙江省二建建设集团有限公司 浙江 宁波 315202；2. 重庆交通大学土木工程学院 重庆 400074；3. 浙大宁波理工学院土木建筑工程学院 浙江 宁波 315100

宁波地区位于我国东南沿海一带，受台风灾害影响严重，精确估计台风地区的极值风速是开展台风灾害风险评估的关键步骤。其中，对台风路径和强度的预测是重中之重。目前，台风路径和强度的预测主要通过台风路径模拟和风场模拟来实现。台风路径模拟可以分为全路径模拟和局部路径模拟两类。需要指出的是，由于我国东南沿海地区历史台风样本数据较少，运用局部路径模拟将无法保证模拟精度[1]；而全路径模拟则很好地克服了这一缺点。

Vickery等[2]提出了一种基于整个海域的热带气旋全路径模拟方法。该方法采用路径及强度回归模型模拟热带气旋的演化全过程，包括起始点生成、行进路径、行进方向、洋面强度发展以及登陆强度衰减等。

不同于采用经验回归模型模拟热带气旋路径的方法，Powell等[3]、Emanuel等[4]采用马尔科夫链方法模拟了热带气旋路径演化全过程。在台风风场模拟方面，已有相当多的风场工程模型问世，并且已有许多学者应用这些台风风场工程模型对中国东南沿海地区的台风气候进行了模拟，Li等[1]采用基于Chow的Vickery模型进行了中国东南沿海若干重点城市的台风危险性分析并估计得到了不同重现期下台风极值风速。

基于模拟与实测台风风速的对比，研究验证了基于Chow的Vickery模型在中国东南沿海地区的适用性。谢汝强[5]详细阐述了Yan Meng风场模型和Thompson and Cardone风场模型的求解步骤，通过数值模拟建立了我国沿海城市广州、深圳、香港和厦门的台风关键参数概率分布模型，并获得了重点城市的模拟台风极值风速序列，进而推算得到了不同重现期下的极值风速值。

除极值风速外，风向也是风场特性的重要参数。实测数据表明，在一个台风袭击目标城市的全过程中，其风向变化较大，往往会改变风向达120°以上[6]，这表明各个风向的极值风速具有一定的相关性，因此需要通过构造联合概率分布函数来更为合理地考虑风速风向的相关关系，更加精确地估计重现期极值风速。

黄铭枫等[7]为了合理确定建设场地的结构抗风设计风速，提出了基于Copula函数的多风向极值风速估计方法，并对杭州地区风环境进行了分析。全涌等[8]对模拟台风数据和良态风数据进行组合，结合风速风向分布模型提出了一种考虑风向的极值风速估计方法，并利用此方法对上海地区极值风速值进行了估计。

本文基于CMA-STI热带气旋最佳路径数据集并采用Vickery经验回归模型进行了西北太平洋海域台风全路径模拟，生成了600年台风路径及强度数据，采用Yan Meng风场模型确定了影响宁波地区的台风风速序列。使用Weibull分布模型描述了台风各风向下的极值风速边缘分布，利用t-Copula函数构造各风向极值风速的联合分布模型，得到了台风考虑风向相关性的多风向极值风速值，并与不考虑风向相关性的多风向极值风速值及规范设计风速值进行了对比。

1 台风全路径模拟

1.1 全路径模拟流程

图1为单个台风全路径模拟流程，共分为5个部分，分别为建立起始点模型、建立行进模型、建立强度模型、路径及强度模拟结果检验、建立台风风场模型和边界层模型，最终生成大量符合历史样本特征的热带气旋路径及强度随机事件样本集。

图1 单个台风全路径模拟流程

1.2 宁波地区台风风速序列的模拟

1.2.1 建立起始点模型

基于CMA-STI热带气旋最佳路径数据集[9]，统计得到历史台风年发生次数变化规律，其可用负二项分布来拟合[2]，通过Monte-Carlo抽样即可获得模拟台风的年发生次数，结合从历史起始点样本中随机抽取的单个台风信息（包括经纬度、移动速度、朝向、中心最低气压等）即可建立起始点模型。

1.2.2 建立行进和强度模型

式（1）为Vickery的经验回归模型[2]，分为移动速度和朝向两部分，可用于模拟西北太平洋海域台风的路径演化过程。

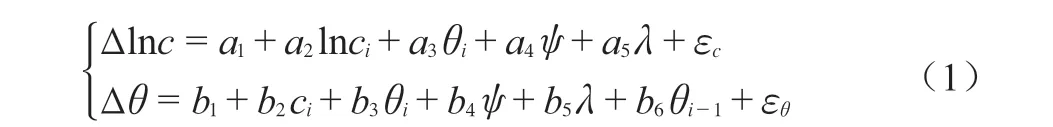
式中：a1、a2、…，b1、b2、…——常数，数值大小与地理区域有关；

ψ——纬度；

λ——经度；

ci——第i步的平移速度；

θi、θi-1——第i及i-1步的风向；

εc、εθ——符合正态分布的零均值随机扰动项。

强度模型分为洋面强度发展模型和登陆强度衰减模型两类，分别用式（2）[2]和式（3）[10]进行模拟。

式中：I——相对强度；

Ts——洋面温度；

εI——符合正态分布的零均值随机扰动项；

d1，d2，…，d6——回归系数。

其中，ti+1－ti＝6 h；Δp（ti）和Δp（ti+1）分别为当前时间点和下一个时间点台风中心气压差；模型系数a0、a1和零均值正态分布随机扰动项的εa标准差σε－可分别通过历史登陆台风的中心气压差数据进行回归分析确定。

1.2.3 路径及强度模拟结果检验

根据李强等[11]中提到的方法对模拟结果进行检验，分别比较了模拟台风与历史台风参数统计值（即年发生率、朝向、移动速度、中心气压差的平均值和标准差），验证了台风全路径模型的有效性。

1.2.4 台风风场模拟

基于上述全路径台风模拟得到的600年台风路径及强度随机样本，采用Yan Meng模型[12]进行宁波地区台风环境分析。

图2所示为台风全路径模拟中激活风场模型的示意图。图中宁波地区位置由三角形标注，当台风中心进入三角形250 km范围内，表示宁波地区受该台风影响。图3给出了影响到宁波地区的距地面10 m高度处10 min不区分风向的台风样本风速序列。

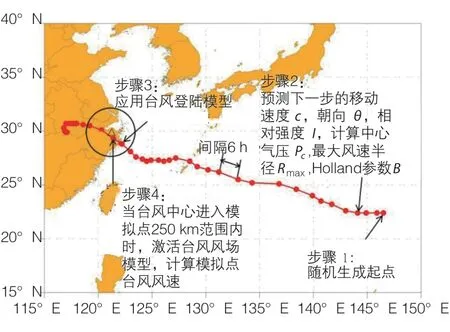
图2 全路径模拟中激活风场模型示意

图3 不区分风向的台风样本风速序列

2 台风多风向极值风速估计

2.1 联合概率分布建模

构造多风向极值风速的联合概率分布函数是考虑风向相关性的有效方法，本文出现的相关性均是指不同风向的极值风速相关性[7]。

考虑风向相关性的联合概率分布函数，如式（4）所示。

式中：Vd1, Vd2,...,VdN——N维极值风速变量中第1，2，…，N个方向的极值风速；

F (vd1,...,vdN)——Vd1, Vd2,…, VdN联合分布函数。

根据Sklar定理[13]，设 FVd1(vd1),..., FVdN(vdN)为N维极值风速变量Vd1,Vd2,…, VdN的边缘分布函数，那么存在一个多维Copula函数C (u1,u2,…, uN)，ui=FVdi（vdi）， i = 1,2,…,N ，满足下式：

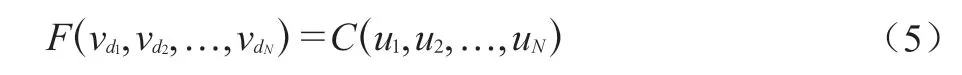
2.2 边缘分布模拟

通过台风全路径模拟得到了宁波地区台风样本风速序列（不区分风向），样本数量巨大，因此可以根据图4将台风风速序列划分到16个风向（D1，D2，…，D16表示16个风向，每22.5°为一个风向），得到每个风向的经验分布。图5给出了风向2和风向15的台风风速经验分布，其很好地服从weibull边缘分布模型式（6）。

图4 风向方位角定义

图5 年极值风速边缘分布曲线

式中：vi——随机风速序列；

λ——比例参数；

k——形状参数。

表1给出了不考虑风向相关性10、50、100 a重现期下16个风向角的极值风速估计值，同时给出了中国荷载规范规定的对应重现期下的设计风速值作为比较。可以发现，宁波地区的最大风速主要集中于风向2，而仅在风向6、7、8、9下，荷载规范给出了较为保守的风速估计值，其余风向均给出了偏于风险的风速估计值。

表1 不同重现期下各风向角极值风速（不考虑风向相关性）单位：m/s

2.3 联合分布模拟

以采用weibull模型估计得到的年最大风速分布作为边缘分布，选择拟合优度最好的t-Copula函数来构造多风向极值风速的联合概率分布模型，采用极大似然法估计t-Copula函数的参数。

表2所示为相关矩阵中相邻风向的相关系数，可以看出，宁波地区台风相邻风向的相关系数均超过0.7，风向2至风向8间的相邻风向相关系数甚至达到了0.99，而有关研究[14]指出，当相邻风向间的相关系数超过0.7时，应考虑相邻风向间的相关性。

表2 相关矩阵中相邻风向的相关系数

其中风向13—14下的联合概率密度等值线如图6所示，可以看出，考虑风向相关性下风向13和风向14的极值风速呈正相关关系，而不考虑风向相关性下，风向13和风向14则没有表现出相应关系，因此，考不考虑相关性，联合概率密度呈现出明显差异。

图6 联合概率密度等值线

根据cook假设[15]，若假设各风向极值风速相等，则可通过式（7）计算得到考虑风向相关性的全风向极值风速vd。

若假设各风向角上的超越概率p相等，则可通过式（8）计算得到考虑风向相关性的R年重现期下各风向极值风速vd1,…,vdN。

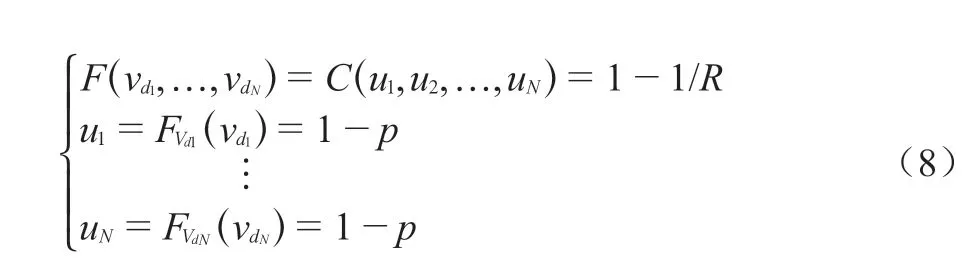
式中：vd——R年重现期下的全风向极值风速值；

vd1,…,vdN——R年重现期下的各风向极值风速值；

u1,…,uN——各风向极值风速边缘分布函数；

C——t-Copula函数。

图7给出了通过式（7）并采用t-Copula函数计算得到的全风向最大风速分布曲线和假设各风向相互独立的年最大风速分布曲线比较，可以看出，考虑风向相关性和风向独立的两条曲线随着重现期的增大有相互靠近的趋势，说明相关性随着重现期的增大在逐渐减弱，但两条曲线相互靠近的速率并没有很快，进一步说明宁波地区台风相邻风向间有很明显的相关关系。

图7 全风向年最大风速分布

根据式（8）计算得到了如图8所示不同重现期下各风向极值风速等超越概率p变化曲线，估计得到了10、50、100 a重现期对应的超越概率分别为3.19%、0.59%、0.29%。

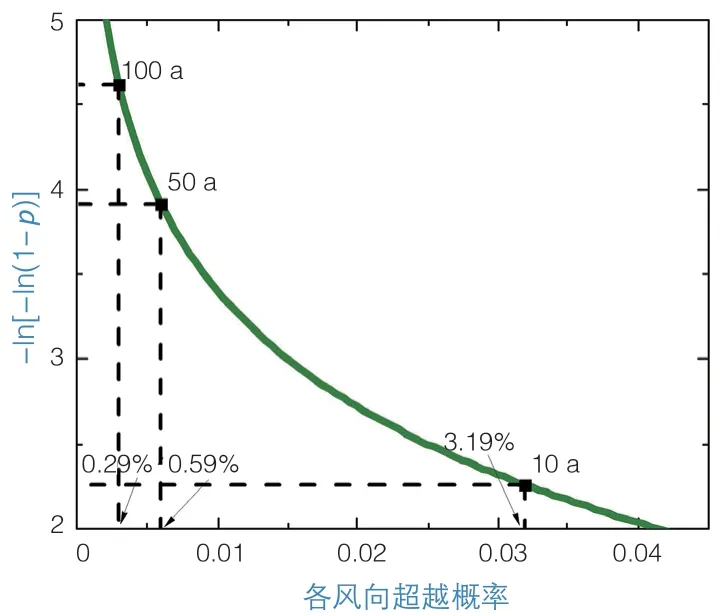
图8 不同重现期下各风向极值风速等超越概率p变化曲线

将各风向不同重现期下的超越概率代入各风向边缘分布模型中，得到考虑风向相关性的各风向极值风速估计值（表3）。

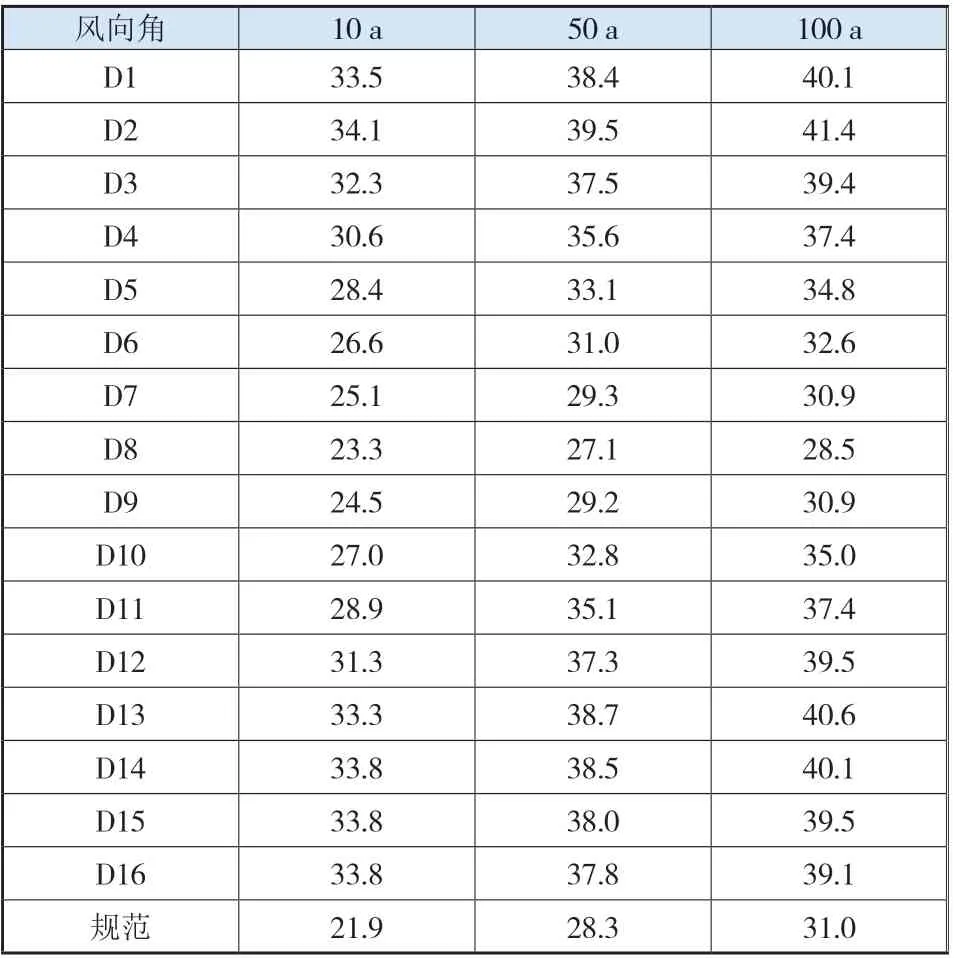
表3 不同重现期下各风向角极值风速（考虑风向相关性）单位：m/s

图9给出了50 a重现期下极值风速考虑相关性和不考虑相关性的估计值与规范设计风速值之间的对比，可以看出，考虑相关性的极值风速值明显大于不考虑相关性的极值风速值，而除了风向8以外，考虑风向相关性的其余各风向极值风速估计值均大于规范设计风速值，说明规范给出的设计风速值偏于危险；除此之外，风向2作为最大极值风速的来流风向，其10、50、100 a的极值风速值分别为34.1、39.5、41.4 m/s。

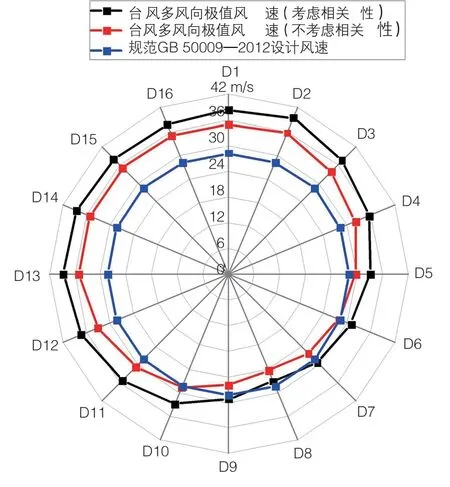
图9 50 a重现期下各风向角极值风速值

3 结语

1）基于CMA-STI热带气旋最佳路径数据集并采用Vickery经验回归模型进行了西北太平洋海域台风全路径模拟，生成了600年台风路径及强度数据，并采用Yan Meng风场模型确定了经过宁波地区的台风风速序列。

2）采用weibull分布模型描述了模拟台风风速序列各风向角下的极值风速边缘分布，得到了不考虑相关性各风向极值风速估计值，与规范设计风速值对比，结果表明规范设计风速值在除风向6、7、8、9以外的其余风向下均给出了偏于风险的极值风速设计值。

3）采用t-Copula函数构造各风向极值风速的联合分布模型来考虑各风向之间的相关性，得到了重现期超越概率以及重现期极值风速，与不考虑相关性的极值风速值对比，结果表明不考虑风向相关性在各风向下给出的极值风速估计值都偏风险；与规范设计风速对比，结果表明规范设计风速值在除风向8以外的其余风向下均给出了偏于风险的极值风速设计值。