基于流动单元分类的致密砂岩储层渗透率预测

鲁健康，郝彬，李程善，王维斌，王乾右，杨威*

1 中国石油大学(北京)油气资源与探测国家重点实验室，北京 102249

2 中国石油大学(北京)非常规油气科学技术研究院，北京 102249

3 中国石油勘探开发研究院西北分院，兰州 730020

4 中国石油长庆油田分公司勘探事业部，西安 710018

5 利物浦大学地球海洋与生态科学系，英国利物浦 L69 3GP

0 引言

渗透率是衡量岩石允许流体通过的畅通程度的参数，是储层评价以及开发的关键参数之一[1,2]，在较均质的常规砂岩储层中，孔隙度与渗透率具有良好的相关性，利用岩心实测数据可建立孔隙度与渗透率的回归模型[3]。为提高渗透率的解释精度，国内外学者提出了不同的模型及计算方法[4-5]：如Jennings和Lucia等[6]基于岩石构系数提出了广义渗透率模型，Bryant等[7]通过建立高精度的地质模型对渗透率进行预测，Mathisen等[8]借助于测井应用数学统计方法计算渗透率，廖东良等[9]提出分流动单元计算渗透率的方法。近几年，随着人工智能技术在石油工业中的应用，越来越多的学者开始利用机器学习、大数据分析、BP神经网络等方法综合预测储集层参数[10-11]：如王依诚等[12]基于机器学习方法构建数字岩心的渗透率快速预测方法，黄雨阳[13]等联合NMR与MICP参数建立了储层渗透率的智能预测方法，王猛等[14]采用区域测井大数据分析进行渗透率建模，张言辉[15]建立了渗透率预测的BP神经网络模型提高渗透率的计算精度。

鄂尔多斯盆地中南部地区长6储层为一套致密砂岩储层，由于受后期成岩作用影响导致储层的孔隙结构和物性发生变化，储层非均质性较强，在同一孔隙度下储层的渗透率相差一到两个数量级。通过对研究区储层的岩心实测孔隙度、渗透率进行相关性分析发现数据点离散，相关性较差，运用单一回归分析方法建立渗透率解释模型，拟合度差、精度低不能满足储层评价以及后期开发的要求[16-18]。因此，为了准确求取渗透率满足储层评级及储层开发的需求，建立一套高精度的渗透率计算方法非常必要。

本文基于流动单元理论对储层进行分类，并利用测井参数计算致密砂岩储层渗透率的方法，该套方法计算精度高，应用效果好，可以很好的利用测井资料预测致密砂岩储层渗透率的空间分布，为以长6储层为代表的陆相致密砂岩储层的后期开发提供有价值的参考。

1 研究区概况

研究区位于鄂尔多斯盆地陕北斜坡中南部，内部构造简单，为平缓西倾大单斜，倾角小于1°，多发育小型低幅鼻状隆起。长6油层组以实际地层的岩性、电性组合特征为出发点，按旋回分出长61、长62、长63和长64四个亚油层组[17]，沉积相为三角洲前缘亚相沉积，储集砂体为分流河道、水下间湾、河口坝、席状砂沉积，岩性以粉砂岩、粉砂质泥岩和泥质粉砂岩为主，局部发育暗色泥岩，及其与灰白色细砂岩、粉砂岩互层[18]，主要发育微裂缝、残余粒间孔、杂基孔和粒内溶孔等多种孔隙类型[19]，长6砂组整体孔渗分布不均匀，储层非均质性较强。

2 样品及数据分析

本次选用研究区6口取心井3个亚油层组的共103块样品的孔渗实测数据进行相关研究。孔隙度与渗透率测试由长庆油田公司勘探开发研究院分析实验中心测试。目的层孔隙度分布在0.3%～16.2%范围内，平均为 8%，渗透率分布在(0.036～23.691)×10-3μm2，平均为0.83×10-3μm2，孔隙度和渗透率数据的分布区间及个数进行统计发现孔隙度小于12%的样品占85.44%，渗透率小于1×10-3μm2的占84.74%(图1)。

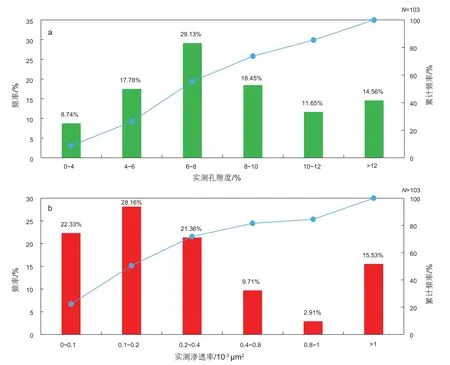
图1 鄂尔多斯盆地延长组长6油层组致密砂岩储层孔隙度、渗透率样品个数及频率分布图Fig.1 The number and frequency distribution of tight sandstone reservoirs in the Chang 6 oil-bearing formation of Yanchang Formation in the Ordos Basin

对实测孔隙度和实测渗透率进行回归来求取研究区实测渗透率与孔隙度之间的定量关系(图2)，二者的总体趋势呈正相关，渗透率随着孔隙度的增大而增大。直接利用孔渗拟合得到的渗透率计算模型其R2值大小为0.4316，用该方法计算得到的渗透率，不能满足储层评价及开发中渗透率精细解释的精度要求。

图2 鄂尔多斯盆地三叠系延长组长6油层组致密砂岩储层孔隙度渗透率交会图Figure 2 Intersection diagram of porosity and permeability of tight sandstone reservoirs in the Chang 6 oil-bearing group of the Triassic Yanchang Formation in the Ordos Basin

储集层分类评价是解决非均质的有效途径[5]，为探究在垂向上渗透率的分布情况，按油层组对目的层的实测孔渗数据进行孔渗相关性分析(图3)，长61、长62、长63三个油层组的R2分别为0.4208、0.1528、0.5532，各亚油层组内部的孔渗的相关性较差，说明对于非均质较强的致密砂岩储层按照亚油层组来研究储层的孔渗关系效果较差。

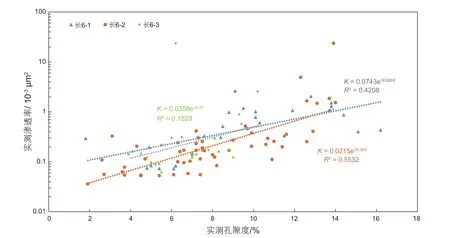
图3 鄂尔多斯盆地延长组长61、长62、长63亚油层组孔渗交会图Fig.3 Porosity and permeability intersection diagram of the Chang 61, Chang 62, and Chang 63 sub-oil layers of the Yanchang Formation in the Ordos Basin

3 流动单元

流动单元的概念最早是由Hearn C L于1984年提出的[20]，他认为流动单元是：垂向及侧向上连续、具有相似渗透率、孔隙度和层面特征的储集带。流动单元的发育特征和空间分布状况受沉积作用、构造作用、成岩作用等不同程度控制[9,21-22]，因此可以用流动单元来综合反映储层的岩石物性特征。而储层由于在沉积过程中受到多种沉积、成岩以及后生作用的影响，因此一个储层可以划分为多个岩石物理性质各异的流动单元，而在同一个流动单元内部，岩石的物理性质和渗流特征具有相似性，所以通过对储层划分不同的流动单元进行储层孔渗关系的研究是可行且合理的。

目前关于流动单元的划分方法经历了从定性划分、半定量划分到定量划分的过程[23-24]：其中定性划分方法包括露头沉积界面分析法，岩心定性分析法，沉积岩相分析法，沉积、成岩、构造作用综合法；定量划分方法有流动分层指数划分法，非均质综合指数法、孔喉几何形状法、多参数分析法，层次分析法，动态流动单元研究法，生产动态资料法等[25-27,33]。目前，以流动分层指数法和多参数定量分析法应用最为广泛，取得较好效果。但是多参数分析法存在参数的选取上不统一，不同学者研究的侧重点不同，其参数选取存在差异，导致其应用效果存在较大差异。流动带指数法是把岩石矿物特征、储层孔喉特征及结构特征等综合起来表征孔隙几何特征的参数，所以利用流动分层指数法进行储层流动单元的划分，可较准确地描述储层非均质特征[28]。

3.1 流动单元的基本原理

Kozeny和Caman根据哈根—泊谡叶和达西定律推导出岩石储层孔隙度和渗透率之间的关系式Kozeny-Caman方程式：

式中，K为渗透率，10-3μm2；φe为有效孔隙度，%；Fs为形状系数；τ为孔隙介质的迂曲度；Fsτ2为Kozeny常数，其为一个变常数，其值在不同的岩石物理相是不同的，在同一个岩石物理相内部其值是一个常数，在实际储层中取值范围为5～100；Sgv为单位体积颗粒的表面积，μm2。

推导得出流动分层指数FZI:

流动分层指数FZI是岩石微观孔隙结构特征的反映，其是将岩石结构和矿物地质特征、孔喉特征等结合起来的一个综合判定参数，因此，可以用其较准确地描述油藏的非均质特征[29]。

3.2 流动单元的划分

根据统计学原理，在相同条件下对同一事物重复多次测量或试验观测的结果应该服从正态分布的规律，对于同种流动单元内样品的测量相当于对该流动单元内单一样品的多次测量的结果，如果某一物理量在线性坐标下的形态为正态分布曲线，那么在正态概率坐标上的形态就近似为一条直线[30-32]。由于随机误差的存在，同一流动单元的FZI围绕其真实均值呈正态分布不同流动单元具有不同的孔喉特征和不同的正态分布函数，所以当存在多个非均质流动单元时，FZI整体分布是若干正态分布的叠加，因此在正态概率坐标上表现为具有不同斜率的直线段[33]。

选用研究区6口取心井的长61、长62、长63三个亚油层组的103块岩心分析数据计算流动分层指数并做出研究区流动分层指数的累计概率分布图(图4)。可以看出图中明显存在多条不同斜率分布的曲线，将不同斜率曲线的交点作为流动单元划分的界限值，将研究区长61、长62、长63划分为4个流动单元。

图4 鄂尔多斯盆地延长组长6油层组流动分层指数累计概率分布图Fig.4 Cumulative probability distribution map of flow unit index of Chang 6 reservoir of Yanchang Formation in Ordos Basin

4类流动单元的具体参数如(表1)所示，第I类储层流动分层指数小于0.4，平均孔隙度为11%，平均渗透率为0.217×10-3μm2，属于“高孔低渗”储层；第Ⅱ类储层流动分层指数0.4～0.8，平均孔隙度为8.5%，平均渗透率为0.387；第三类储层流动感单元指数0.8～1.5，平均孔隙度为6.8%，平均渗透率为0.711×10-3μm2，这两类储层物性相对较好；第Ⅳ类储层流动分层指数大于1.5，平均孔隙度为4.6%，平均渗透率为5.095×10-3μm2，属于“低孔高渗”储层，该类储层微裂缝发育。

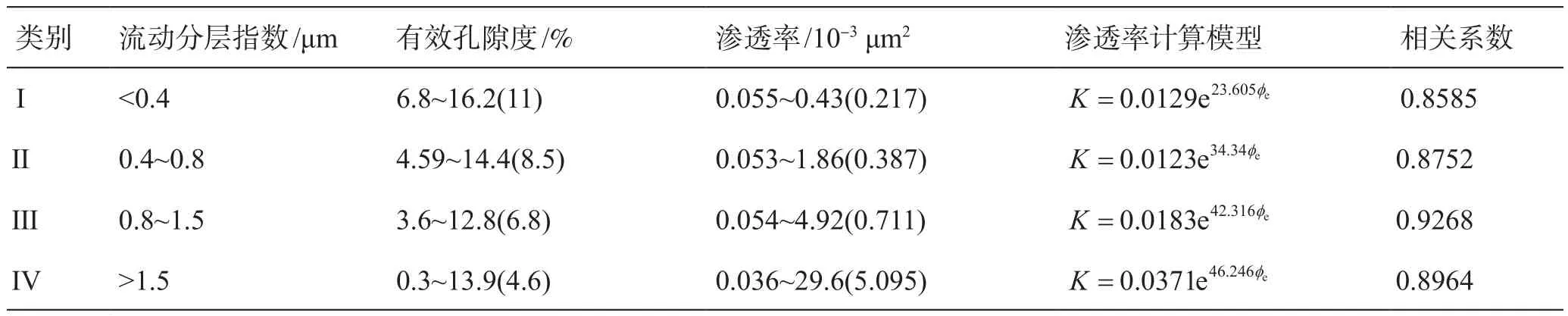
表1 长6油层组基于流动分层指数的分类标准及渗透率计算模型Table 1 Classification criteria and permeability calculation model of Chang 6 reservoir group based on flow unit index

根据流动单元可以将研究区长6储层划分为4种流动单元，在用流动单元划分的基础之上对研究区的实测孔渗参数进行拟合，可以清楚的看到在分流动单元之后各类储层孔隙度、渗透率计算模型的R2平均达到了0.8892，大幅提高了预测准确率(图5)。

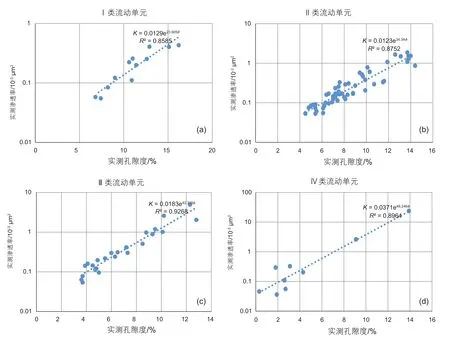
图5 划分流动单元之后实测孔隙度渗透率交会图Fig.5 Intersection diagram of measured porosity and permeability after dividing flow units

4 孔隙度和流动分层指数的测井计算

为了将利用岩心分析数据进行流动单元划分进行渗透率计算的方法在未取心的地区进行推广，所以考虑用测井曲线进行流动分层指数的计算，对未取心井的地区进行流动单元划分。同时通过测井曲线与孔隙度之间的相关性拟合进行孔隙度的计算。

4.1 孔隙度的测井计算

对数据中的异常数据值进行剔除，选取其中典型样品的数据进行孔隙度和测井参数以及经过测井参数进行换算得到的参数进行相关性分析，其分析结果见表2。

根据分析结果显示SH(通过SP曲线计算得到的泥质含量曲线)、SP曲线与孔隙度相关性最好，且与孔隙度值呈负相关，也符合泥质含量越高孔隙度值越小的地质规律。通过SPSS软件对孔隙度和测井参数进行多元回归，采用逐步回归的方法，该方法会对不符合统计标准的变量进行剔除，以得到最优的模型。最终孔隙度的计算模型：

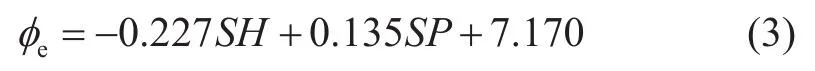
式中，SH为泥质含量，%；SP为自然电位，mV。

利用该模型计算出得到的孔隙度拟合度较高，其R2值为0.879，满足精度要求。

4.2 流动分层指数的测井计算

由于取心成本的限制，只对研究区少数的关键井进行了取心，研究区内的大部分井都没有进行取心。在有取心的井段可以直接利用岩心法分析数据结合Kozeny-Caman方程来计算流动分层指数进行储集层分类。而未取心的井段，就不能进行流动分层指数的计算。前人研究发现测井曲线和流动分层指数之间有相关性，可以通过测井参数建立流动分层指数与测井响应之间的定量关系进行未取心井段的流动分层指数的计算，然后再进行储集层分类[27-28]。

建立储层流动分层指数与测井响应的函数关系。首先分析测井参数和流动单元之间的相关性，选取对流动分层指数敏感性较强的测井参数进行回归分析，建立流动单元与测井曲线之间的函数模型，进行流动单元的测井计算。通过对研究区测井参数与流动分层指数(FZI)进行相关性分析，分析结果如表2所示。

表2 流动分层指数、孔隙度、测井曲线相关性分析Table 2 Correlation analysis of flow unit index, porosity and logging curve

利用SPSS进行多元回归得到利用测井参数计算流动分层指数的计算模型如下所示：

式中，Δt为声波时差，单位μs/m。

通过该方法拟合得到的流动单元计算模型精度较高，其R2值为0.812，拟合度高。

4.3 实例应用

将本次研究推导出的渗透率计算模型在研究区典型单上进行应用，具体流程如下：首先根据式(3)计算出地层的有效孔隙度φe，然后利用式(4)计算流动分层指数FZI，再根据前面的流动单元划分标准将流动单元划分为4类，最后利用每种流动单元的渗透率计算模型计算每一类流动单元的渗透率。其应用效果如图6、图7所示，利用FZI方法分类后计算的渗透率曲线，与岩心实测渗透率对比，绝对误差0.26×10-3μm2，相对误差19.14%；利用测井计算得到的FZI与利用岩心实测计算得到的FZI拟合程度较好。用本次研究的模型计算出的渗透率整体上和岩心实测渗透率拟合度较高，满足储层精细评价的要求，计算精度较高。本次研究为该地区没有取心井的地区渗透率的精确计算提供了很好的依据。

图6 S-001计算渗透率与岩心分析渗透率对比图Fig.6 Comparison of S-001 calculated permeability and core analysis permeability

图7 S-002计算渗透率与岩心分析渗透率对比图Fig.7 Comparison of S-002 calculated permeability and core analysis permeability

5 结论

(1)利用流动单元对储层进行分类可以很好的提高渗透率的解释精度，使得渗透率计算模型的拟合度由0.4316提高到平均0.8892，大幅提高了预测准确度。

(2)建立了流动分层指数、有效孔隙度的测井计算模型，模型的拟合度均达到0.8以上。形成了一套利用分流动单元结合测井资料求取鄂尔多斯盆地中南部地区长6致密砂岩储层渗透率的计算方法。

(3)应用该套方法对典型单井渗透率进行计算，计算精度高、实际应用效果好，计算得到渗透率的绝对误差为0.26×10-3μm2，相对误差19.14%，实现了渗透率的连续评价，为致密砂岩储层渗透率的精细评价提供了参考。