基于演化博弈的人力稀缺服务行业员工心理幸福感提升策略研究——以养老行业为例

马箭，易丹

(中南大学湘雅医院，湖南长沙，410083；长沙理工大学经济与管理学院，湖南长沙，410114)

一、引言

所有的竞争，归根结底是人才的竞争。在人力稀缺服务行业，人才的流失是行业发展的关键瓶颈，人才的培养是保持行业朝气的活力源泉。在所有的人力稀缺服务行业中，养老服务行业关乎民生、连着民心，是我国所有家庭都参与其中的一个行业，其发展状态直接关乎我国老年人是否真正能够实现“老有所养、老有所依、老有所安”。随着老龄化的加剧，我国的养老服务需求正在迅速增加[1]。联合国国际老龄问题研究所马文・福尔摩萨研究员指出：养老护理人才职业化，对中国迎接人口老龄化的挑战至关重要。影响中国养老事业发展的“瓶颈”并不是养老院、医院、养老设备等硬件资源，而是直接服务于老年人的人力资源。如果根据养老床位建设目标的要求测算，2020年我国大概需要64 万养老护理员，到2050年需要124 万养老护理员，而如果全部失能半失能老人都得到护理，2020年至少需要520 万养老护理员，到2050年则至少需要1314万养老护理员[2]。根据北京师范大学发布的《2017年中国养老服务人才培养情况报告》，我国养老护理员实际数量不足50 万人，持证人员不足2万人，缺口巨大。养老护理员缺乏成为直接制约养老服务行业发展的决定性因素[2-3]。护理人员总量不足且周转率高、专业化不足、男性护理员少等成为养老服务行业共同面临的现实问题[4]。因此，养老服务企业通过制定人力资源管理战略以降低养老护理员流动率就成为养老护理员急缺形势下助力养老服务企业实现可持续发展的关键问题。

民政部发布的一项数据分析报告显示，养老机构服务人员存在“三高、三低”问题，即：女性占比高、人员流动率高、劳动强度高；工资收入低、社会地位低、服务水平低。而护理员招聘难和留住难，更是整个养老产业的普遍窘境[4]。招不到护理员，养老机构就将面临空床率问题，陷入运营困境[5]。而在实地调查中，发现有小部分养老护理员愿意坚持从事这一行业的普遍原因是：与老人相处时，感觉自己特别被需要，是有价值的，心里是富足的、幸福的，而这就是养老护理员所需要的成就感。从中可以看出，类似于一般企业员工[6]，当养老护理员感知幸福时，会选择留职，但感知不幸福时，则很有可能会选择离职。因此，探讨如何培养养老护理员的幸福感，对养老服务机构“招来人、留住人”具有重要的现实意义，是其实现健康发展、可持续运营的关键。

以往关于幸福感的研究更多地聚焦在源于快乐论的主观幸福感，但主观幸福感是通过个体对心理或情感的一种主观认知或即时的体验感知来判断个体是否幸福，只关注个体即时的快乐或愉悦感知，无法反映出个体内心感知的真实状态。20世纪90年代以来，一些心理学研究者认为，仅从快乐论来解释幸福感具有片面性，并不能充分反映人们是否充分挖掘了潜能和开展了健康、积极、向上的生活。因此学者们从实现论出发来诠释幸福感，他们认为幸福不仅仅是获得即时的快乐体验，还需要充分发挥自身潜能，实现人生价值。由此，提出了应用“心理幸福感”来重新解释幸福，以区别于主观幸福感。心理幸福感可以理解为个体潜能充分实现的心理感受及愉悦体验，是一个需要持久努力和投资的动态过程。有部分学者基于员工的工作情境探讨了工作幸福感或职业幸福感，认为它是指工作情境中感知到的幸福感，主要指个体对当前所从事工作的认知评价和情感体验[7]。对于养老护理员而言，其幸福感的影响因素有其独特性，一方面会受工作环境的影响，另一方面，女性为主的群体特征使其幸福感受家庭因素的诸多影响。因此，养老护理员的幸福感会同时受工作与家庭两方面的影响，用工作幸福感或职业幸福感来解释都较为片面，本文选择心理幸福感来体现养老护理员的幸福感。

心理幸福感在动态变化过程中，会受到家庭、工作、组织环境等方面因素的影响[8-10]。繁忙的工作致使养老护理员无暇照顾家庭，另外家庭生活的不顺也可能对护理员的工作状态产生影响，导致工作-家庭的双向角色冲突[11-12]。根据资源保存理论[13]，角色压力可能威胁或导致养老护理员情感资源的耗损，为减轻角色压力，养老护理员努力控制环境，不得不通过各种渠道获取某些资源来弥补情绪资源的损失[14]。角色压力作为养老护理员资源流失威胁的重要途径，可能会使养老护理员产生不安全感，进而演变成工作倦怠、心理幸福感降低等负面的心理感知[15]。因此，由工作-家庭双向冲突产生的角色压力是否会导致养老护理员的心理幸福感降低，取决于养老护理员在应对角色压力时所损耗的资源和养老护理员通过不同渠道获得的资源是否能够维持平衡[14]。组织支持感知能够满足员工对组织的需求，例如希望受到组织的重视和尊重等[16]。从实践上来说，当养老护理员遭到工作-家庭双向冲突所带来的压力时，寻求组织支持是获取组织资源的重要方式，养老服务组织为其提供尊重、情感、工作等方面的支持是提升养老护理员心理幸福感、稳定护理员队伍的关键[12]。但目前我国养老事业处于起步阶段，大多数地区的养老服务组织管理普遍缺乏专业性，难以满足养老护理员对组织支持等资源的获取，致使员工内心感知产生较大的不稳定性。因此，其心理幸福感会随时受到与客户的交互过程、工作-家庭冲突、组织环境等因素的影响[17]。而员工心理与行为状态的变化取决于多方利益相关者的博弈结果，如对资源损耗的博弈、员工与组织的博弈、幸福感影响个体行为决策的博弈等[18-21]。以往关于个体心理幸福感的研究较多关注其影响因素、作用机制、测量维度等方面，较少从演变视角探究个体心理幸福感的动态均衡过程，而个体的心理感知状态达到某一稳定状态，其实质是由自我与外界作用力量之间的耗损与获取这一博弈过程决定的[4,22]。因此可以考虑应用博弈论分析养老护理员心理幸福感的均衡稳态形成过程。相对于经典博弈理论，演化博弈以有限理性为前提，运用策略互动的思想，将传统的纳什均衡精炼为演化稳定均衡[23]，同时引入选择机制构建复制动态模型，更适用于分析养老护理员心理幸福感提升过程中，养老护理员心理幸福感的演化以及多主体互相作用的关系[4]。

基于此，本文针对人力稀缺服务行业的留人难问题，以养老服务行业为例，从养老服务机构和养老护理员耗费各自资源，共同提升养老护理员心理幸福感的策略选择出发，探讨养老服务机构与养老护理员之间均衡稳定策略的形成过程。具体来讲，将针对养老护理员心理幸福感的演化过程，基于演化博弈方法建立养老护理员和养老服务机构之间的演化博弈模型，分析博弈双方反复博弈、学习和策略调整的过程，然后引入其他利益相关主体的“约束-激励”机制，以实现最优的稳定均衡策略，以使养老护理员的心理幸福感处于较高的稳定均衡状态，以期为养老护理员和养老服务机构的策略选择提供科学参考，也为其他人力稀缺行业提升员工心理幸福感及其留职意愿提供参考。

二、问题描述与基础模型

(一)问题描述

以往研究已经证实，在服务行业中，员工个人的内外部资源(心理资本或组织支持感知)对其心理幸福感具有显著的积极影响。同样地，在养老服务行业这一人力稀缺服务行业中，养老护理员感知到的组织支持及其积累的心理资本会对其心理幸福感产生影响。因此，为控制养老护理员心理幸福感的变化，养老服务机构和养老护理员可以采取不同的策略，而该策略的决策过程和结果则是养老服务机构和养老护理员之间演化博弈的结果。

首先，由于提升心理幸福感需要耗费养老护理员的内部资源，因此养老护理员需要考虑是要采取积极的态度还是消极的态度，采取多大程度的积极态度或消极态度，来提升其心理幸福感。养老护理员要考虑采取何种策略来提升其心理幸福感？采取每种策略会获得多少的价值收益或付出多少成本？

其次，养老护理员心理幸福感的稳定或提升有助于增强其对养老服务机构的忠诚度，遏制其离职意愿的产生。当养老护理员想要提升其心理幸福感时，养老护理员需要权衡是消耗个人资源来提升心理幸福感，还是希冀从养老服务机构获取各方面的组织支持来提升其心理幸福感。而养老服务机构的应对策略是养老护理员无法控制的，因为养老护理员和养老服务机构都处于信息不对称的分散决策状态。因此，养老服务机构和养老护理员二者在提升养老护理员的心理幸福感时，由于会消耗各自的资源，使得二者会进行应对策略选择的博弈。养老护理员会希望从养老服务机构获取足够多的支持并消耗尽量少的个人资源来提升心理幸福感，而养老服务机构为养老护理员提供各方面的组织支持来满足养老护理员的需求是需要付出成本的，因此养老服务机构需要决策是否对提升养老护理员的心理幸福感施加帮助。在本研究中，将养老护理员投入个人资源定义为采取积极策略，不投入资源定义为采取消极策略。养老服务机构为养老护理员提供组织支持定义为采取帮助策略，不提供组织支持定义为不帮助策略。

本文依据实际情况，提出下述前提假设：

假设1：养老护理员和养老服务机构均为有限理性行为主体[4]，博弈方始终追求自身利益最大化。

假设2：博弈方分别来自不同的主体，博弈成员间随机配对和相互学习，进行动态重复博弈，其策略选择的过程可以用博弈主体的复制动态方程来模拟。

假设3：养老护理员和养老服务机构进行博弈，养老护理员的策略空间为｛积极，消极｝；养老服务机构的策略空间为｛帮助，不帮助｝。“积极-帮助”策略是社会所期盼的最优策略。

基于上述分析，本文假设养老护理员拥有的个人内部资源存量(如心理资本)为其带来的效益为χ1，而养老护理员的个人外部资源存量(如组织支持感知，其大小取决于养老服务机构资源投入的程度，可以视为养老服务机构的行为)为养老服务机构带来的效益记为χ2。养老护理员投入个人内部资源(如心理资本)来提升心理幸福感，给其带来的价值收益为π1，耗费的个人内部资源成本为C1；同理，养老服务机构为帮助养老护理员提升心理幸福感，从而达到有效执行养老服务机构的员工发展计划的目的，需要为养老护理员提供某些方面的组织支持来满足养老护理员的需求，假设该行为产生的价值收益为π2，那么为养老服务机构带来的价值收益为π2i，为养老护理员带来的价值收益为π2s，养老服务机构付出的资源成本为C2。由于养老护理员要通过将养老服务机构提供的组织支持转化为个人的外部资源来提升心理幸福感，而该转化程度会直接影响养老护理员心理幸福感提升的有效性，因此本文将养老服务机构供给的组织支持的可转换程度记为μ(μ∈[0,1])，而养老服务机构供给的组织支持最终能够转为养老护理员个人外部资源的程度记为v(v∈[0,1])，因此，有π2s=χ2μν，养老服务机构获取的价值收益则为π2i=π2-χ2μν。需要说明的是，养老机构采取帮助或不帮助，养老护理员采取积极或消极的策略组合过程中，可能会受到其他因素的影响，但为简化分析，本文只关注与该情境有关的关键因素。

但养老护理员或养老服务机构采取何种策略都是不确定的，因此本文假设养老护理员采取消极策略的概率为q1(q1∈[0,1])(采取积极策略的概率记为1-q1)，而养老服务机构采取不帮助策略的概率记为q2(q2∈[0,1])(采取帮助策略的概率记为1-q2)。

涉及的变量与符号说明如表1所示。要使讨论有意义，需令χ1＞0，χ2＞0，π1＞0，π2i＞0，π2s＞0，C1＞0，C2＞0，否则不符合现实情况。

表1 参数符号与说明

(二)基础模型

由于提升养老护理员的心理幸福感需要一个过程，且在该过程中会反复受到不利工作条件的影响(如工作-家庭冲突等)，因此养老护理员和养老服务机构之间资源消耗的策略互动过程可以用演化博弈来描述。在每一期的博弈中，养老护理员和养老服务机构都会进行策略的选择，将养老护理员和养老服务机构分别记为博弈方1 和博弈方2。每一个博弈方案对提升养老护理员的心理幸福感具有的策略集分别为{积极，帮助}、{积极，不帮助}、{消极，帮助}、{消极，不帮助}。表2描述了养老护理员和养老服务机构之间的博弈情形。

表2 养老服务机构与养老护理员的博弈矩阵

向量组{χ1-C1+π1+χ2μv,χ2-C2+π2-χ2μv}、{χ1+π1-C1,χ2}、{χ1+χ2μv,χ2+π2-C2-χ2μv}、{χ1,χ2}分别代表了养老护理员和养老服务机构采取{积极，帮助}、{积极，不帮助}、{消极，帮助}和{消极，不帮助}时博弈方的收益，括号内的前半部分表示养老护理员的净收益，括号内的后半方表示养老服务机构的净收益。因为养老护理员心理幸福感提升或下降，是养老护理员与养老服务机构各自的策略实施行为共同作用的结果，而养老服务机构的努力可以转化为养老护理员的收益。因此假设养老护理员和养老服务机构的收益都可以帮助提升养老护理员的心理幸福感水平，并通过养老护理员的净收益表示出来。

1.养老护理员心理幸福感演化的稳定策略与均衡点分析

假设养老护理员采取“积极”策略的概率为q1(t)，则采取“消极”策略的概率为1-q1(t)。养老服务机构采取“帮助”策略的概率为q2(t)，则采取“不帮助”策略的概率为1-q2(t)。

那么，养老护理员采取积极策略的期望收益为：

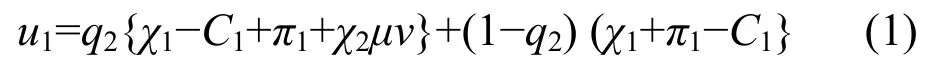
养老护理员采取消极策略的期望收益为：

此时，养老护理员的整体收益为：

因此，养老护理员采取应对策略的复制动态方程为：

养老服务机构采取帮助策略的期望收益为：

养老服务机构采取不帮助策略的期望收益为：

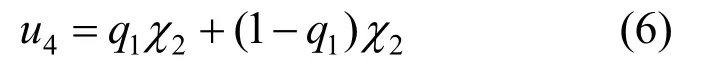
此时，养老服务机构的整体收益为：

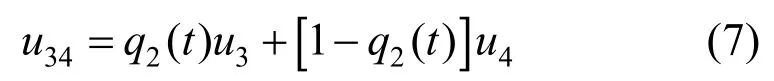
因此养老服务机构采取应对策略的复制动态方程为：

由养老护理员和养老服务机构的复制动态方程构成的利益关系主体的复制动态系统方程如下：

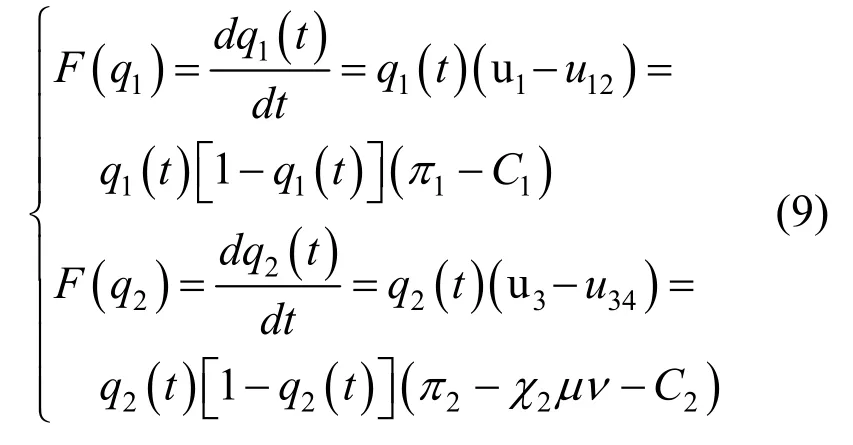
该系统的局部均衡点构成演化博弈均衡策略，养老护理员和养老服务机构都是决策者，相对于个体决策，养老护理员群体的积极(消极)策略和养老服务机构的帮助(不帮助)策略会随着时间发生变化，通过不断地改变他们的策略而获得最大的目标收益。当复制动态方程组F(q2)=0,F(q1)=0 时，养老护理员和养老服务机构的收益均达到均衡状态，得到四个局部均衡点：A(0,0)、B(1,0)、C(0,1)、D(1,1)。

为确定养老护理员心理幸福感提升过程中利益群体关系演变的最终结果，需要对该系统各个局部均衡点进行稳定性分析。Friedman 提出可以应用雅克比矩阵来对局部均衡点的稳定性进行分析，以检验博弈系统的稳定状态[24-25]。对于本研究所涉及的养老护理员心理幸福感演化博弈的动态系统，其雅克比矩阵及其对应的行列式和迹的表达式为：

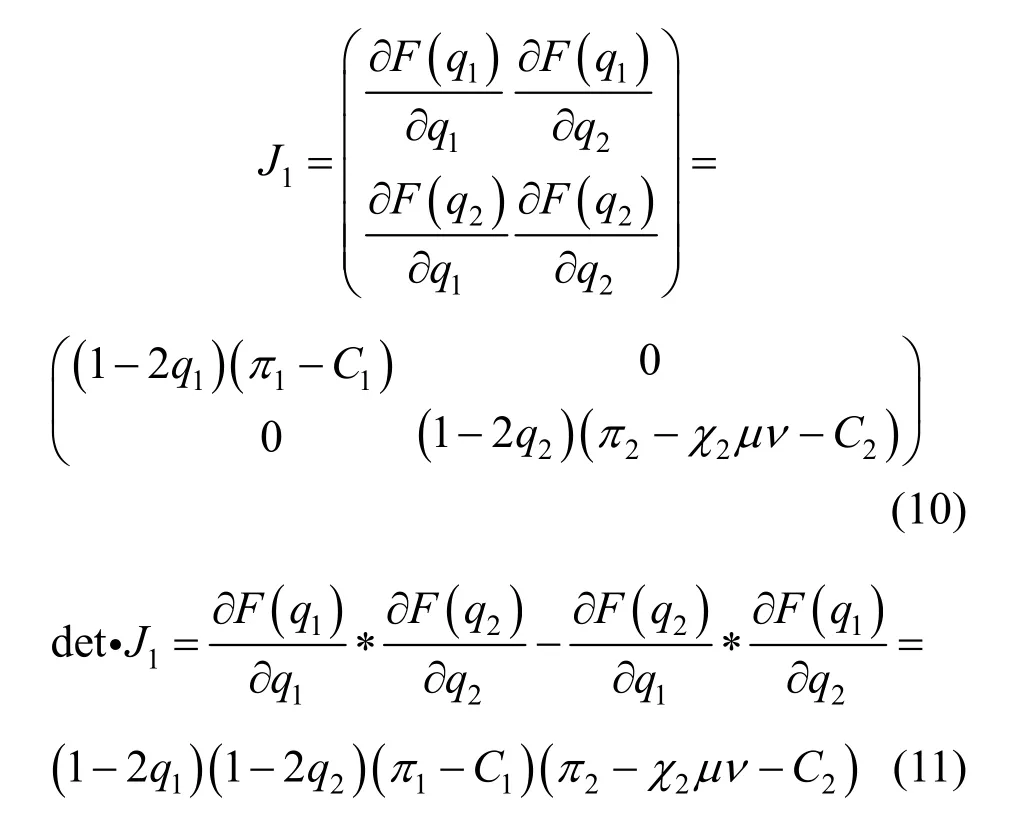
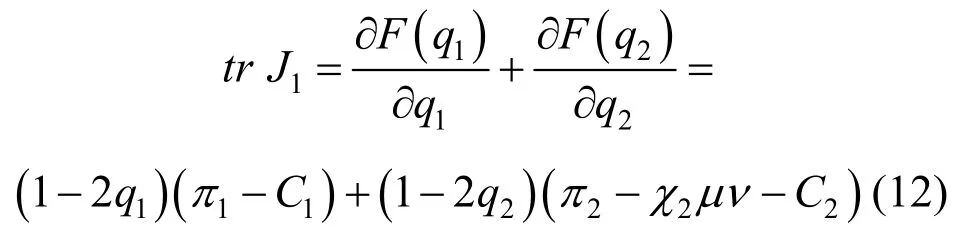
根据雅克比矩阵的局部均衡点稳定性分析法，对四个均衡点进行稳定性分析，结果如表3所示。

表3 四个局部均衡点的稳定性分析结果

从表3可以看出，动态复制系统均衡点的行列式值和迹的正负性与养老服务机构转移给养老护理员的价值收益、养老护理员和养老服务机构的资源存量、获取的收益和耗费资源的成本密切相关。因此，养老护理员和养老服务机构的决策对系统的均衡点起关键作用。

2.养老护理员心理幸福感演化稳定均衡的参数讨论

根据Friedman 提出的应用雅克比矩阵分析系统演化的稳定性的思想[22]，若策略(x,y)是系统均衡的稳定策略，那么行列式Det(J1)和迹Tr(J1)应满足Det(J1)＞0 和Tr(J1)＜0。由以上分析可知，系统的稳定均衡点取决于养老护理员和养老服务机构的资源存量、获取的收益和耗费资源的成本的大小。因此可以分为四种情况进行讨论，每种情形下的行列式Det(J1)和迹Tr(J1)如表4所示。

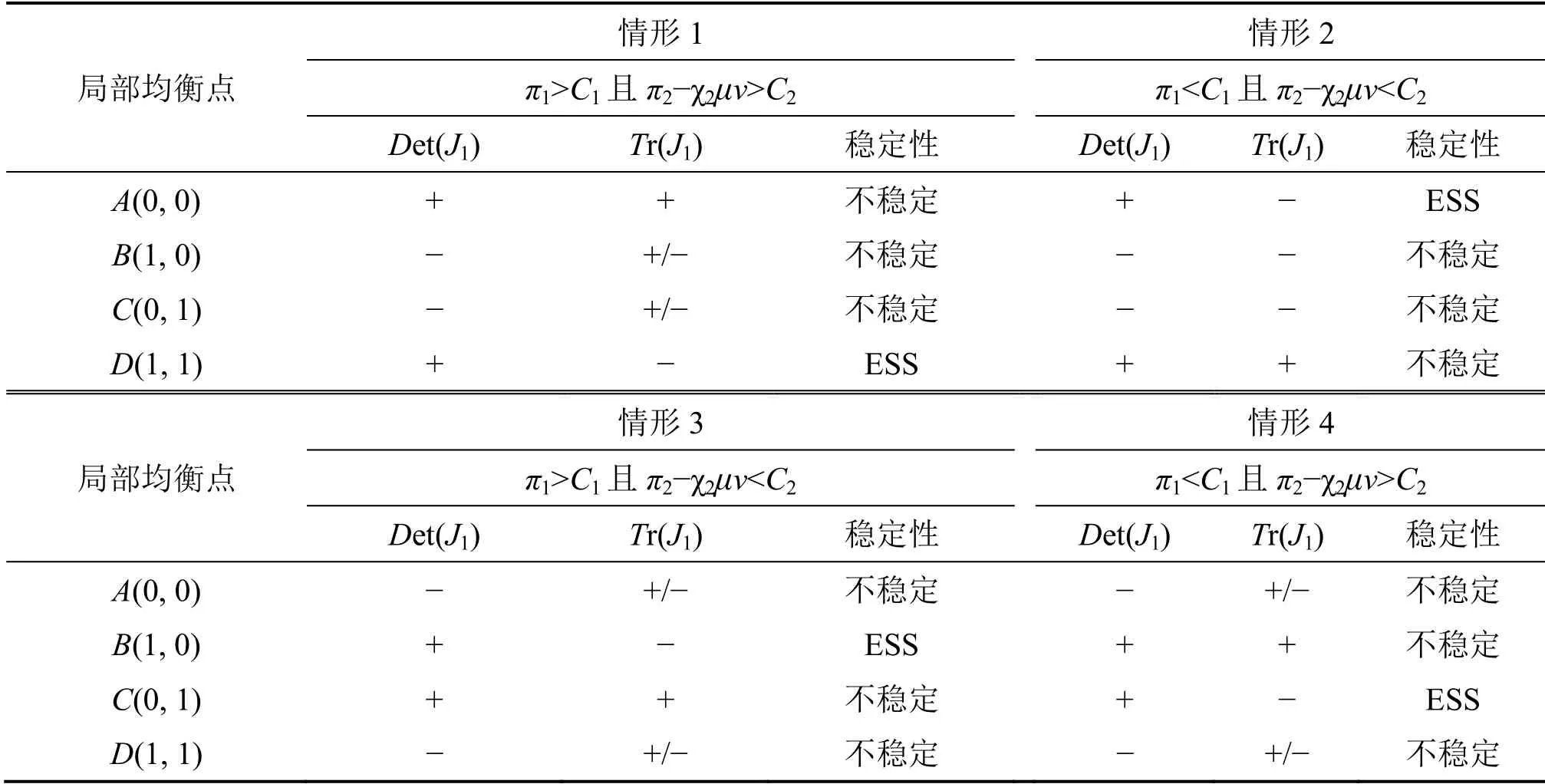
表4 均衡点的稳定性分析结果

情形1：当π1＞C1且π2-χ2μv＞C2时，根据雅克比矩阵的均衡条件可知：对局部均衡点A(0,0)，有Det(J1)＞0、Tr(J1)＞0，因此点A(0,0)不符合均衡条件；对局部均衡点B(1,0)，有Det(J1)＜0，而Tr(J1)的取值大小取决于养老护理员和养老服务机构净收益之差，有可能为正值，也有可能为负值，因此点B(1,0)不符合均衡条件；对局部均衡点C(0,1)，有Det(J1)＜0，而Tr(J1)的取值大小取决于养老护理员和养老服务机构净收益之差，有可能为正值，也有可能为负值，因此点C(0,1)不符合均衡条件；对局部均衡点D(1,1)，有Det(J1)＞0、Tr(J1)＜0，因此点D(1,1)符合均衡条件，是该系统演化的博弈均衡点。由此可知，当养老护理员和养老服务机构的收益均大于成本时，二者分别采取“积极”策略、“帮助”策略，此时能够最大限度地提升养老护理员的心理幸福感，从而使得养老护理员积极地为入住老年人提供高质、高效的养老服务。

情形2：当π1＜C1且π2-χ2μv＜C2时，根据雅克比矩阵的均衡条件可知：对局部均衡点A(0,0)，有Det(J1)＞0、Tr(J1)＜0，因此点A(0,0)符合均衡条件，是该系统演化的博弈的均衡点；对局部均衡点B(1,0)，有Det(J1)＜0、Tr(J1)＜0，因此点B(1,0)不符合均衡条件；对局部均衡点C(0,1)，有Det(J1)＜0、Tr(J1)＜0，因此点C(0,1)不符合均衡条件；对局部均衡点D(1,1)，有Det(J1)＞0、Tr(J1)＞0，因此点D(1,1)不符合均衡条件。这表明，当养老护理员和养老服务机构采取措施提升养老护理员的心理幸福感时，其所获得的收益如果小于所耗费的资源成本，那么养老护理员和养老服务机构无论最初采取什么策略，最终的稳定均衡点都是{消极，不帮助}。同时也表明，期望的最优稳定均衡策略{积极，帮助}，无法通过养老护理员或养老服务机构自身的演化来实现，如果想要实现最优稳定均衡策略，需要进行制度、政策、老年人态度、社会公众认可等方面的适当干扰。如当老年人对养老护理员提供的服务非常满意时，老年人及其家属给予肯定和赞扬，可以使养老护理员从工作中获得满足感并提升其心理幸福感，进而使得养老护理员积极地为老年人和养老服务机构创造更多的价值。

情形3：当π1＞C1且π2-χ2μv＜C2时，根据雅克比矩阵的均衡条件可知：对局部均衡点A(0,0)，有Det(J1)＞0，Tr(J1)的取值大小取决于养老护理员和养老服务机构净收益之差，有可能为正值，也有可能为负值，因此点A(0,0)不符合均衡条件；对局部均衡点B(1,0)，有Det(J1)＞0、Tr(J1)＜0，因此点B(1,0)符合均衡条件，是该系统演化的博弈的均衡点；对局部均衡点C(0,1)，有Det(J1)＞0、Tr(J1)＞0，因此点C(0,1)不符合均衡条件；对局部均衡点D(1,1)，有Det(J1)＜0，而Tr(J1)的取值大小取决于养老护理员和养老服务机构净收益之差，有可能为正值，也有可能为负值，因此点D(1,1)不符合均衡条件。由此可知，当养老护理员采取措施提升心理幸福感时，如果其收益大于耗费的资源成本，那么无论养老服务机构采取何种措施，最终相关利益群体的最优稳定均衡策略为{积极，不帮助}。

情形4：当π1＜C1且π2-χ2μv＞C2时，根据雅克比矩阵的均衡条件可知：对局部均衡点A(0,0)，有Det(J1)＞0，Tr(J1)的取值大小取决于养老护理员和养老服务机构净收益之差，有可能为正值，也有可能为负值，因此点A(0,0)不符合均衡条件；对局部均衡点B(1,0)，有Det(J1)＞0、Tr(J1)＞0，因此点B(1,0)不符合均衡条件；对局部均衡点C(0,1)，有Det(J1)＞0、Tr(J1)＜0，因此点C(0,1)符合均衡条件，是该系统演化博弈的均衡点；对局部均衡点D(1,1)，有Det(J1)＜0，而Tr(J1)的取值大小取决于养老护理员和养老服务机构净收益之差，有可能为正值，也有可能为负值，因此点D(1,1)不符合均衡条件。这说明当养老护理机构采取措施帮助养老护理员提升其心理幸福感时，如果养老服务机构的收益大于耗费的资源成本，而养老护理员的收益小于耗费的资源成本，那么无论养老护理员采取何种措施，最终相关利益群体的最优稳定均衡策略为{消极，不帮助}。

三、引入“约束-激励”机制的养老护理员心理幸福感演化博弈模型

从以上研究中可以看出，选取何种策略组合，取决于养老护理员和养老服务机构各自的收益与成本的大小。当养老护理员采取的应对措施的收益大于资源耗费成本，而养老服务机构的收益小于资源耗费成本时，即使养老服务机构不采取任何应对措施，养老护理员也能够有效地提升其心理幸福感。同理，当养老服务机构采取应对措施帮助养老护理员提升其心理幸福感的收益大于资源耗费成本，而养老护理员的收益小于资源耗费成本时，即使养老护理员不采取任何应对措施，养老服务机构采取的积极应对措施也能够帮助养老护理员有效地提升其心理幸福感。但当养老护理员和养老服务机构各自的收益小于资源耗费成本时，养老护理员和养老服务机构就会陷入“囚徒困境”，使得{消极，不帮助}策略成为演化均衡策略。因此为避免双方陷入非合作博弈，必须引入外界力量的“约束-激励”机制来进行控制。

以往的研究主要关注针对养老护理员或养老服务机构，如何设计机制以约束其行为的问题。因为从现实中来说，养老护理员与养老机构之间是相互依存的关系，养老护理员需要养老服务机构提供工作机会来获取报酬或者实现自身价值，而养老服务机构则需要一支稳定的、专业的养老护理员队伍来维持其正常运营，从而为入住老年人提供满意的养老服务。当养老服务机构未提供养老护理员所需的组织支持时，可能会对养老护理员的心理幸福感产生消极影响，甚至促使养老护理员做出如虐待老人等以损害服务质量为代价来报复养老服务机构的反生产行为。同理，养老护理员不采取积极应对措施时，也会为养老服务机构带来服务质量等方面的损失。

但是养老服务行业属于劳动密集型行业，需要进行大量的“管理员工”的工作，仅对不利组织的行为进行惩罚所带来的效果远低于惩罚与激励并行的机制。而现有研究对如何同时设计“约束-激励”机制以使养老护理行业的利益主体做出利组织行为，或主动提升服务质量还鲜有说明。因此，本部分试图在考虑惩罚消极行为的基础上，设计约束-激励机制，来督促养老护理行业的利益主体(养老护理员、养老服务机构)采取最优策略有效提升养老护理员的心理幸福感，为老年人提供优质服务提供护理员队伍保障。

假设当养老护理员对提升心理幸福感采取“积极”策略，而养老服务机构采取“帮助”策略为养老护理员提供组织支持以帮助其提升心理幸福感时，其他利益主体(如政府、老年人、社会公众)会对两者进行一定的奖励，用B表示。例如，由于养老护理员为老年人提供的是“关系型”服务，当养老护理员和养老服务机构共同努力克服养老护理员遭遇的工作-家庭等外部干扰问题，并致力于提升养老护理员的心理幸福感时，养老护理员会因为心理幸福感的提升而以更加积极的姿态为老年人提供服务，并向老年人传递正能量，使老年人的老年生活得到充实；而老年人在养老服务机构良好的生活状态，会使得其家属对养老护理员和养老服务机构提供的养老服务认可，从而使养老护理员获得工作为其带来的成就感、满足感和幸福感，并以更好的工作状态为老年人提供优质服务，以此往复，便形成了利益主体之间价值收益输送的良性循环。因此，外界对养老护理员和养老服务机构工作的认可，可以看作是一种来自社会公众层面的奖励。而就我国养老护理队伍建设情况来看，养老护理员的职业身份得不到公众的认可，是阻碍该职业群体发展的主要因素之一。此外，假设养老护理员或养老服务机构二者中有一方采取“消极”/“不帮助”策略的话，会产生一定的社会成本，主要表现为其他利益主体对其行为进行的惩罚，惩罚成本为A。此时，养老护理员和养老服务机构的博弈收益矩阵如表5所示。

表5 引入“约束-激励”机制的养老服务机构与养老护理员的博弈矩阵

(一)演化稳定策略分析

1.养老护理员的演化稳定策略分析

在其他利益主体的“约束-激励”机制下，养老护理员采取积极策略的期望收益为：

养老护理员采取消极策略的期望收益为：

此时，养老护理员的整体收益为：

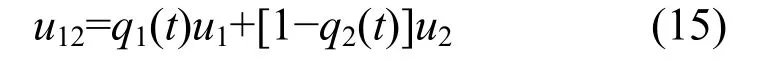
因此养老护理员采取应策略的复制动态方程为：

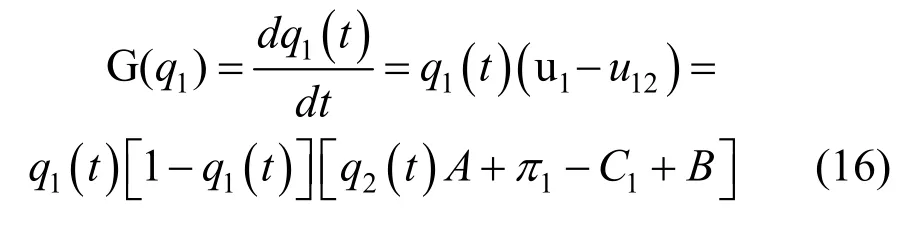
令G(q1)=0，可以得到养老护理员采取应对策略的复制动态方程的两个稳定均衡点，即q*1=0和q*1=1。

①如果q2=q*2=(C1-π1-B)/A，且0≤(C1-π1-B)/A≤1 时，那么G(q1)=0 恒成立，这说明当养老服务机构按q2=(C1-π1-B)/A的水平采取“帮助”策略时，养老护理员选择“积极”策略或者“消极”策略的收益并没有显著区别。

②如果q2＞q*2=(C1-π1-B)/A，那么q*1=0 和q*1=1 是两个可能的稳定均衡点。对G(q1)求导，可以发现G′(1)＜1，因此q1=1 是演化博弈的稳定策略。这意味着当养老服务机构以大于(C1-π1-B)/A的水平选择“帮助”策略时，养老护理员的策略选择逐渐从“消极”向“积极”转变，最终使“积极”策略成为稳定均衡策略。从上述分析可知，当A 越大时，q2＞q*2=(C1-π1-B)/A的条件越容易满足，说明养老服务机构采取“帮助”策略的可能性越大，同时也表明，当其采取“不帮助”策略的惩罚成本越大时，越容易获得最优的稳定均衡策略。

③如果q2＜q*2=(C1-π1-B)/A，那么q*1=0 和q*1=1是两个可能的稳定均衡点。对G(q1)求导，可以发现G′(0)＜1，因此q1=0 是演化博弈的稳定策略。这意味着当养老服务机构以小于(C1-π1-B)/A的水平选择“帮助”策略时，养老护理员的策略选择逐渐从“积极”向“消极”转变，最终使“消极”策略成为稳定均衡策略。

2.养老服务机构的演化稳定策略分析

在其他利益主体的“约束-激励”机制下，养老服务机构采取帮助策略的期望收益为：

养老服务机构采取不帮助策略的期望收益为：

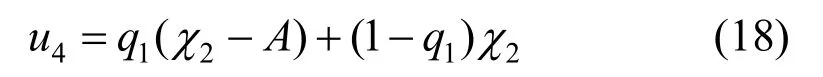
因此养老服务机构采取应对策略的复制动态方程为：

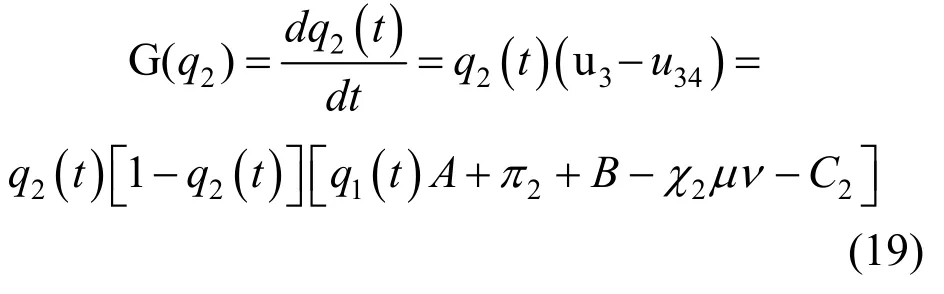
令G(q2)=0，可以得到养老服务机构采取应对策略的复制动态方程的两个稳定均衡点，即q*2=0 和q*2=1。

①当q1=q*1=(χ2μv+C2-π2-B)/A，且0≤(χ2μv+C2-π2-B)/A≤1 时，那么G(q2)=0 恒成立，这说明当养老护理员按q1=(χ2μv+C2-π2-B)/A的概率采取“积极”策略时，养老服务机构在帮助养老护理员提升心理幸福感时，选择哪种策略的收益并无明显差别。

②如果q1＞q*1=(χ2μv+C2-π2-B)/A，那么q*1=0和q*1=1 均是稳定的均衡点。在对G(q2)求导后，可以发现G′(1)＜1，因此q1=1 是演化博弈的稳定策略。类似于对养老护理员采取应对策略时的复制动态方程的分析思路，当养老护理员以大于(χ2μv+C2-π2-B)/A的概率选择“积极”策略时，养老服务机构的策略选择逐渐从“不帮助”向“帮助”转变，最终使“帮助”策略成为稳定均衡策略。因此，当惩罚成本A 越大时，q2越大于均衡解q*2=(C1-π1-B)/A，同时也表明，养老服务机构采取“帮助”策略的可能性越大，越容易获得最优的稳定均衡策略。

③如果q1＞q*1=(χ2μv+C2-π2-B)/A，那么q*1=0和q*1=1 均是稳定的均衡点。类似于对养老护理员采取应对策略时的复制动态方程的分析思路，首先对G(q2)求导，可以发现G′(0)＜1，因此q1=0 是演化博弈的稳定策略。这说明当养老护理员以小于(χ2μv+C2-π2-B)/A的概率选择“积极”策略时，养老服务机构的策略选择逐渐从“帮助”向“不帮助”转变，最终使“不帮助”策略成为最优稳定均衡策略。

(二)“约束-激励”机制下养老护理员心理幸福感稳定均衡的参数讨论

根据上述分析，可以得到由养老护理员和养老服务机构的复制动态方程构成的利益关系主体的复制动态系统，如式(20)：

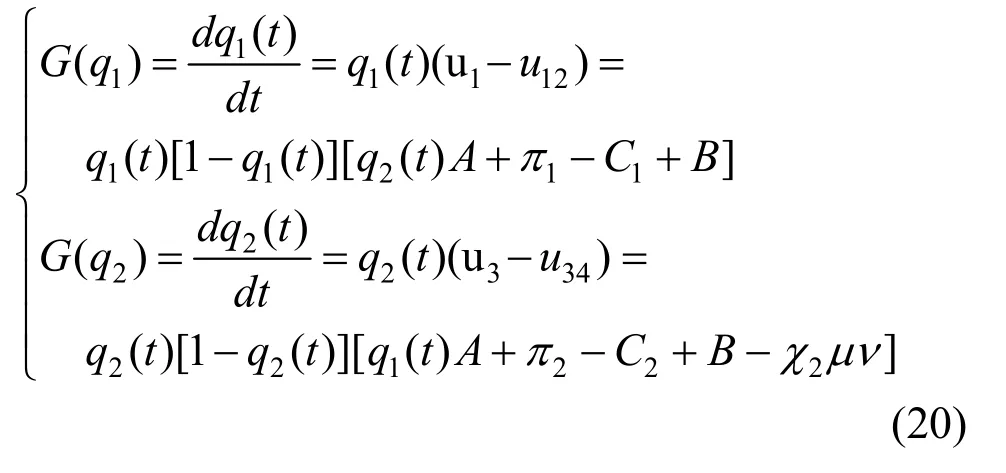
在其他利益主体的“约束-激励”机制下，可以得到由养老护理员和养老服务机构的复制动态方程构成的利益相关主体的复制动态系统的演化博弈模型的五个均衡点，即A(0,0)、B(1,0)、C(0,1)、D(1,1)、E(q*1,q*2)。引入“约束-激励”机制后，根据Friedman 的思想，可以得到养老护理员心理幸福感演化博弈的动态系统，其雅克比矩阵及其对应的行列式和迹的表达式为：

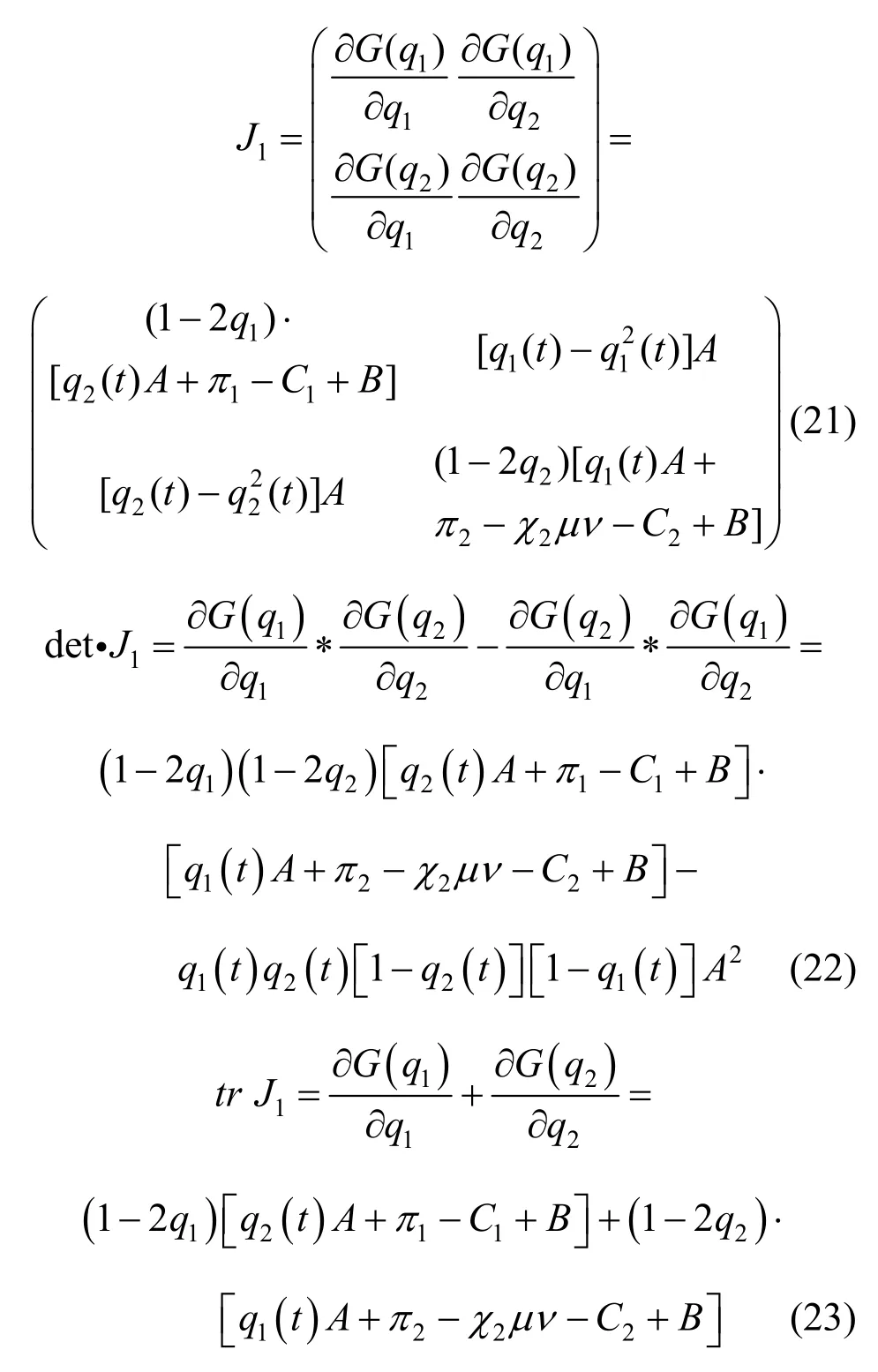
根据雅克比矩阵的局部均衡点稳定性分析方法，对五个均衡点进行稳定性分析，结果如表6所示。

从表6可以看出，引入“约束-激励”机制后，养老护理员心理幸福感演化的动态复制系统均衡点的行列式值和迹的正负性与养老服务机构转移给养老护理员的收益、养老护理员和养老服务机构的资源存量、获取的收益和耗费资源的成本、选择“积极”策略/“帮助”策略的奖励和选择“消极”策略/“不帮助”策略的惩罚密切相关。由此可见，养老护理员和养老服务机构的决策，以及其他利益相关主体对养老护理员和养老服务机构的策略实施行为施加的约束和激励，对系统的均衡点起关键作用。因此，需要根据养老护理员和养老服务机构的收益/成本参数和“约束-激励”参数值的大小来判断演化博弈的均衡点。由前述分析可知，当π1＞C1且π2-χ2μv＜C2时，策略B(1,0)为唯一稳定均衡策略，此时只要养老护理员的收益大于资源耗费成本，那么无论养老服务机构采取何种策略，都能实现最优的稳定均衡策略。同理，当π1＜C1且π2-χ2μv＞C2时，策略C(0,1)为唯一稳定均衡策略，此时养老服务机构从积极采取措施帮助养老护理员提升心理幸福感的行为中获得的收益足够高时，即使没有外界干预或养老护理员的积极行为时，仍然可以帮助养老护理员有效提升其心理幸福感。而π1＞C1且π2-χ2μv＞C2时，可以得到最优稳定均衡策略D(1,1)。因此本部分只需考虑及π1＜C1且π2-χ2μv＜C2的情形。根据演化博弈的思想，策略D(1,1)为理想的最优稳定均衡策略，根据表6可知，针对稳定性参数，存在以下几种情形需要进行探讨。

表6 五个局部均衡点的稳定性分析结果

根据“约束-激励”机制下局部均衡点的稳定性分析结果可知(详见表7)，在情形1、情形3和情形4 中，仅存在唯一的稳定均衡策略D(1,1)；而在情形2 中，存在两个稳定均衡策略A(0,0)和D(1,1)。从复制动态方程的相位图中可以看出，只有满足情形1、情形3 和情形4 时，引入“约束-激励”机制情况下的养老护理员心理幸福感的演化博弈才存在唯一的最优稳定均衡策略{积极，帮助}。在此情况下，可以得出其他利益相关主体实施的“约束-激励”机制的相关参数的取值范围(奖励B 和惩罚成本A)：

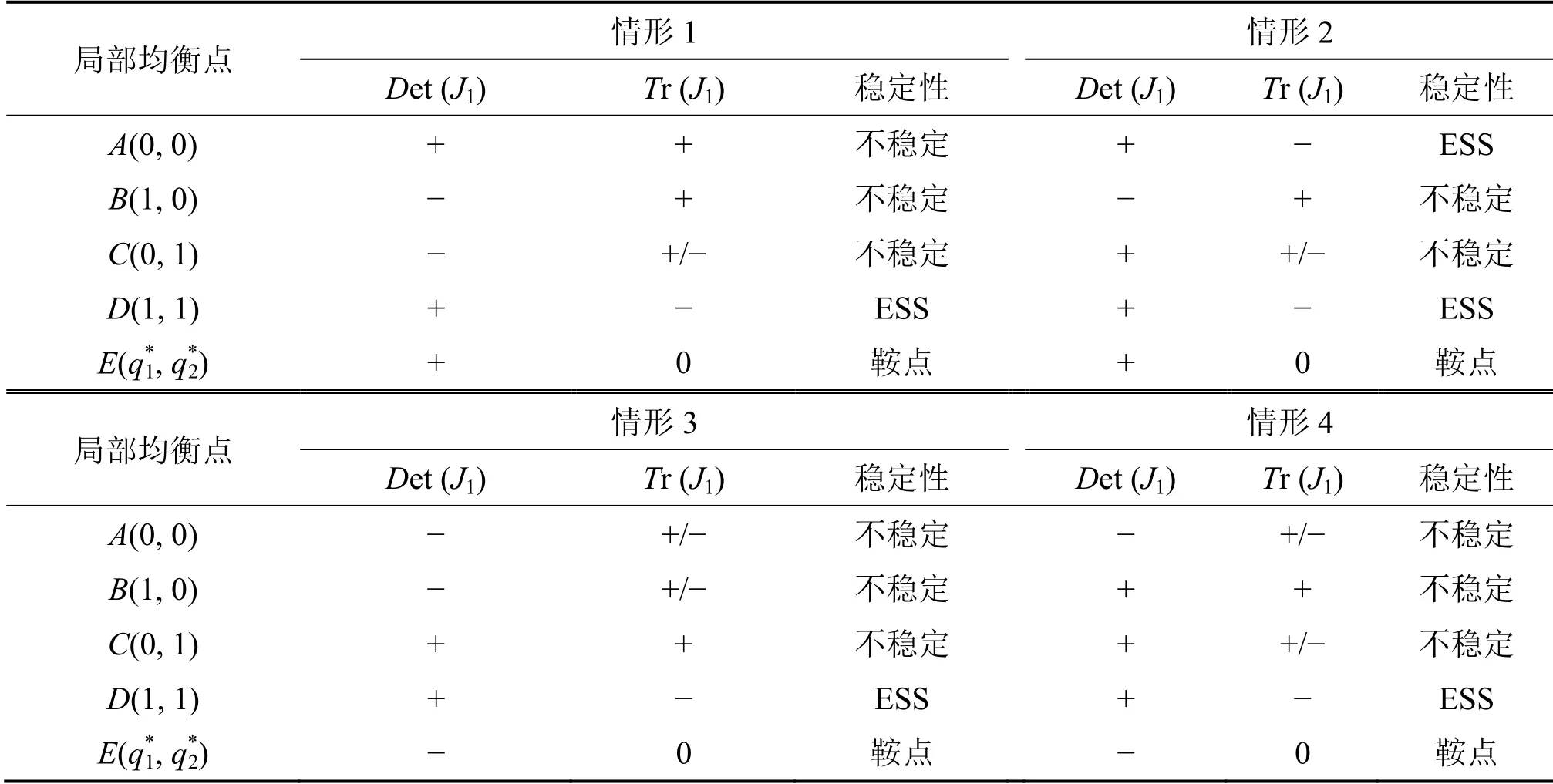
表7 “约束-激励”机制下局部均衡点的稳定性分析结果

这说明其他利益相关主体施加的奖励和惩罚成本之和不仅要大于养老护理员耗费个人资源以提升心理幸福感所造成的损失，而且要大于养老服务机构为帮助养老护理员提升心理幸福感所造成的损失。

四、研究结论与启示

在服务行业中，人才稀缺是制约其发展的关键因素之一，而对于养老服务行业来说，由于该类服务具有生产与消费的同时性，养老护理员为该服务的直接生产者，使得该制约作用尤为明显。在服务过程中，养老护理员的心理幸福感知会显著影响其工作状态，且该影响过程会受到工作-家庭冲突等外界因素的干扰。在养老服务行业，养老护理员为老年人提供的是“关系型服务”，因此养老护理员的工作状态对服务质量至关重要，可以说，养老护理员个人状态的好坏直接决定了老年人是否能够享受到优质的护理服务。在养老服务机构为老年人提供服务产品的过程中，涉及多个利益主体，如养老服务机构、养老护理员、老年人及其家属、政府监管部门等，各主体间的利益关系错综复杂，且各主体之间的利益关系不仅表现为经济价值，还存在某些类型的服务价值。因此，在提升养老护理员的心理幸福感过程中，考虑各主体间的博弈行为以实现最优稳定均衡策略是非常有必要的。

养老护理员心理幸福感演化过程的实质是一个利益博弈再调整的过程，最终目的是提升养老护理员的心理幸福感，使其以更加积极的态度为老年人提供高质、高效的护理服务。但在没有其他利益相关主体施加“约束-激励”机制的情况下，很难实现最优的稳定均衡策略。主要原因在于，养老护理员绝大多数为40～60 岁的女性，该群体具有文化程度低、处在更年期、需要兼顾工作与家庭等显著特征，在护理老年人的过程中需要耗费大量的情绪劳动，而处理工作与家庭关系也同样需要耗费大量的情绪劳动，这两个情绪耗费过程会显著影响其心理幸福感知。因此养老护理员会希望养老服务机构给予一定的组织支持来克服不利工作条件，以降低个人资源的损耗，而养老服务机构则需要对为养老护理员提供组织支持所创造的价值与耗费的资源成本进行权衡。该过程就构成了养老护理员和养老服务机构之间的博弈过程。其中，养老护理员和养老服务机构各自都以实现自身利益最大化为目标，在博弈过程中可能会损害到老年人享受到的服务品质，因此需要引入包括老年人在内的其他利益相关主体施加的“约束-激励”机制来帮助实现最优均衡稳定策略{积极，帮助}。

基于上述分析，促进人力稀缺服务行业的发展，需要从多方面发力，本文以养老服务行业为例，提出如下几点管理建议：(1)有效激发养老护理员和养老服务机构的积极性与能动性，结合二者自身的特点，以最低的资源损耗成本改善不利工作条件，提升养老护理员的心理幸福感，使二者采取应对策略的收益大于付出的资源成本。(2)充分发挥包括老年人在内的其他利益相关主体的重要作用。引入其他利益相关主体主导的“约束-激励”机制，一方面，充分发挥其他利益相关主体的监督作用，对养老护理员和养老服务机构可能会做出不利于提升养老护理员心理幸福感的行为进行约束；另一方面，对养老护理员和养老服务机构的积极行为给予肯定和认同，激发其积极性和创造性，特别是要使养老护理员从得到认可的工作中获得心理满足感和幸福感，进而使其认同职业身份，有效提升留职意愿。(3)政府部门要足够重视老年护理服务行业的发展，可采取补贴职业培训、宣扬“夕阳天使”等措施，破解养老护理员的身份认同困境，尽快建立一支稳定、专业，能够满足我国老年护理需求的职业队伍。