三维重建中先验概率重加权点云配准算法

孙志亮，张荣国，赵 建，李富萍，胡 静

(太原科技大学 计算机科学与技术学院，太原 030024)

三维重建的目标是高质量地捕捉物体和场景的三维形状和外观[1]，在景物深度信息已知的条件下，只需要经过点云数据的配准及融合，即可实现景物的三维重建。点云配准的目标是将一个点云与另一个点云对齐来估计最佳的相对变换，是计算机视觉、计算机图形学和移动机器人学中的一项基础性工作。在大多数情况下，点云是通过扫描设备从不同的视角捕捉到的，所得到的点云不可避免地会有噪声和外点。同时由于部分重叠和遮挡，点云之间也存在对应位置缺失。因此，点云配准在许多实际应用中仍然是一个具有挑战性的问题。

解决配准问题的经典解决方案是迭代最近点(Iterative Closest Point，ICP)算法及其变体。ICP假设一对一的对应关系，并通过最小化对应点距离，迭代地建立最近邻对应关系。由于ICP算法概念简单，在实际应用中性能良好，出现了大量基于ICP的改进和应用[2]。然而，ICP算法在面对大量外点、噪声和对应位置缺失时，通常会陷入局部最优。因此，大量的工作使用概率模型处理噪声和外点，并通过建立一对多的对应提高算法的鲁棒性和配准精度[3-9]。

大多数概率配准方法使用高斯混合模型GMM(Gaussian Mixture Mode)，关键在于其概念简单并且对噪声鲁棒。基于GMM的配准方法通常将两个点云的配准问题看作概率密度估计问题，将一个点云视为GMM质心，然后通过估计目标函数的最大似然实现配准，如CPD、HGM和FilterReg.最近BCPD针对CPD中的收敛性和效率问题做出改进，在变分贝叶斯推理下实现配准。此外，最小化两个概率分布之间的距离也能实现配准，如SVR[10]和MLMD[11]。

另一种用于配准的概率模型称为学生-t混合模型(Student’s t Mixture Model，SMM)，SMM与GMM相比，对外点更加鲁棒。为了解决非刚性点云配准的对应位置缺失和大量外点，DSMM[12]基于SMM在贝叶斯框架下寻找对应，并引入Dirichlet分布处理对应位置缺失。与此相关的工作是TLMM[13]，其提出了一种分层贝叶斯网络点云配准方法。尽管基于SMM的方法显示出更好的鲁棒性，但是在目标函数优化过程中，精度和效率之间的权衡仍然是一个具有挑战性的问题。

此外，解决点云配准问题的新趋势是基于学习的配准方法，如DeepGMR[9]借鉴基于GMM的配准方法，使用神经网络估计GMM的参数。然而这类方法需要庞大的数据集进行训练，泛化性比较差。

上述方法的着眼点均在寻找更准确的位置对应关系，在存在大量的外点和对应位置缺失时配准结果不理想，并且对平面结构较多的点云表现不佳。为此，本文提出了一种结合点到面距离和先验概率加权的点云配准方法。首先，点云之间的位置对应关系通过高斯混合模型和均匀分布来建立；其次，对应位置缺失通过重新加权GMM的混合比例来处理，潜在外点及其比率通过后验概率推测；然后，向误差函数中添加目标点的法线，用点到面距离衡量点云之间相似性，从而更好地处理平面结构较多的点云。最后，本文算法与期望最大化(Expectation-Maximization，EM)算法融合，并在求解GMM参数时移除潜在的外点来提高算法准确性。实验结果表明本文配准方法对点云中的外点、对应位置缺失和平面结构均具有较好的表现。

1 相关研究

1.1 基于GMM的点云配准

对两片维度为D的点云，一片点云表示目标点云Y=(y1,…,yN)∈RN×D，另一片表示源点云X=(x1,…,xM)∈RM×D，其中M和N分别是源点云和目标点云中点的个数。目标点云Y可以构造为GMM并作为GMM的质心，源点云X看作GMM产生的观测数据，并通过估计GMM的最大似然实现配准。在配准期间目标点云的位置不变，源点云的位置由变换参数θ控制，即：

xi(θ)=Ti(θ)xi=Rixi+ti

(1)

其中Ti(θ)∈SE(3)是仅依赖于点xi的刚体变换；Ri∈R3×3xi是旋转矩阵；ti∈R3是平移向量。GMM具有以下形式：

p(xi)=

(2)

通过假设源点云独立同分布，目标点yj对应的后验概率为P(yj|xi)=αjp(xi|yj)/p(xi).变换参数θ和协方差σ2通过最小化下面的负对数似然函数来计算：

(3)

1.2 EM算法

EM算法用来查找GMM中变换参数θ和协方差σ2闭式解。在E步，根据估计的θ和σ2，使用贝叶斯(Bayes)定理计算GMM质心的后验概率P(yj|xi)，进而得到对应关系；在M步固定P(yj|xi)，通过最小化公式(3)重新计算θ和σ2，然后更新源点云位置。EM算法通过E步和M步交替进行，直至收敛。由公式(3)得到目标函数：

(4)

式中，后验概率P(yj|xi)的值为：

(5)

忽略掉公式(4)中独立于θ和σ2的常量，将PDFp(xi|yj)的值代入，得到关于参数θ和σ2的目标函数：

(6)

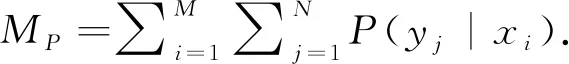
(7)

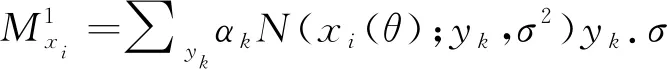
(8)

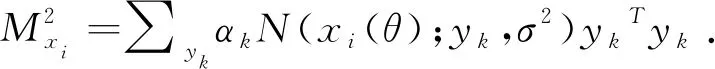
2 本文配准策略

2.1 先验概率重加权

在现有的基于GMM的配准方法中[3，5，6]，GMM分量被指定相同的成员概率1/N，这不能够解释缺失的对应位置关系[12]。目标点云中属于对应位置缺失的点，产生的观测数据与源点云无关，在进行最大似然估计时影响GMM参数的计算精度。因此在每次EM迭代，有必要重新估计GMM成分的混合比例。

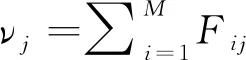
(9)

其中νj=∑xkN(xk(θ);yj,σ2).得到的先验概率向量α用于重新调整GMM分量的混合比例，并以此解决点云配准时的对应位置缺失。

2.2 潜在外点推测

外点是源点云中与目标点云不匹配的点，外点的存在影响GMM参数的计算精度。大多数以前的工作[3-5]需要根据点云之间的匹配程度手动调整外点比率ω，并且在计算GMM参数时没有处理外点，因此本文对源点云中的潜在外点进行处理。

(10)

此外，矩阵P中每一列的和可以解释为每个目标点与源点匹配的概率，矩阵P所有元素的和可以解释为匹配数。因此，外点比率可以计算为：

(11)

2.3 点到面距离

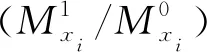
Nxi=∑ykαkN(xi(θ);yk,σ2)

(12)

其中Nyk是点yk的法向，并通过修改公式(7)得到以下点到面形式的误差函数：

(13)

3 算法求解及步骤

3.1 算法求解

本文配准策略融入到EM算法框架下，E步骤具有以下高斯变换形式：

(14)

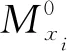
(15)

从而变换参数θ的改变量为Δθ=-A-1b.

3.2 算法步骤

算法名称:点云配准算法

输入：源点云X∈RM×D，目标点云Y∈RN×D

输出：配准后的点云X和Y

Step 1.输入源点云X和目标点云Y；

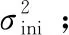
Step 3.获得GMM变换参数θ和协方差σ2以及先验概率向量α；

Step 5.对每个目标点yk，通过PDF计算其产生源点云的概率νj；

Step 6.根据式(9)计算先验概率向量α并重新加权GMM成分，解决对应位置缺失问题；

Step 8.根据式(11)计算外点比率ω；

Step 9.移除潜在外点并通过式(15)求解θ；

Step 10.通过式(1)更新源点云位置xi(θ)；

Step 11.通过式(8)计算σ2;

Step 12.重复Step 3-11，获得最优变换参数θ；

Step 13.根据θ输出配准后的点云X和Y.

4 实验和结果

本文实验环境为 Intel i5-10400 CPU和16 GB RAM，并用Python实现提出的算法。此外，本文用到了Open3D库中的配准评估函数，给定自定义的最大对应距离，该函数返回拟合度和RMSE两个指标。拟合度定义为对应点数C与目标点数N的比值，RMSE定义为对应点之间的均方根误差，即

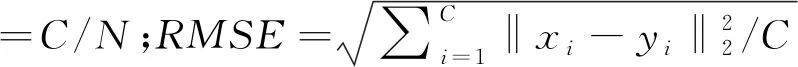
因此，RMSE越低且拟合度越高，配准结果越好。

4.1 合成数据实验

以斯坦福大学3D扫描库中的Bunny，Happy Buddha，Dragon和Armadillo为目标，测试本文算法。首先使用Bunny中的bun000和bun045进行定性分析，其原始点数分别为40 097和40 256，经过0.003体素下采样后分别降低到3 331和3 459.图1(a)和图1(b)显示了本文方法的初始对齐和最终对齐，其中源点云和目标点云分别被标记为红色和蓝色。

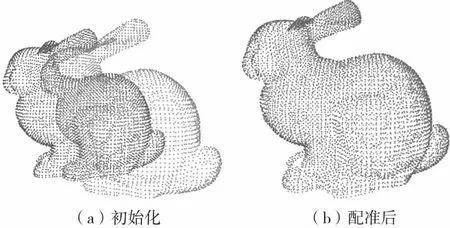
图1 bun000和bun045的配准结果

本文的方法与以下三个算法进行比较：CPD，一种具有代表性的基于GMM的点云配准算法；HGMR，一种用于刚性配准的鲁棒分层随机模型；FilterReg，一种使用参数化旋转和高斯滤波器的高效配准算法。图2(a)和图2(b)是各种算法在不同的最大对应距离下的拟合度和RMSE.本文的方法与其余算法相比，具有更低的RMSE和更高的拟合度，并且在最大对应距离为0.8 mm时已具有较高的准确性。

图2 拟合度和RMSE比较

根据上述实验，另外选择四个具有不同特征的对象来测试配准性能，分别是Armadillo_60/30，Armadillo_60/0，Dragon_48/0和Buddha_48/0.各目标的原始点数和体素下采样后的点数如表1所示。不同算法的拟合度在最大对应距离为1 mm时的结果如图3所示，本文方法在较多的对应位置缺失时，均优于其他比较的方法。

表1 配准目标的点数

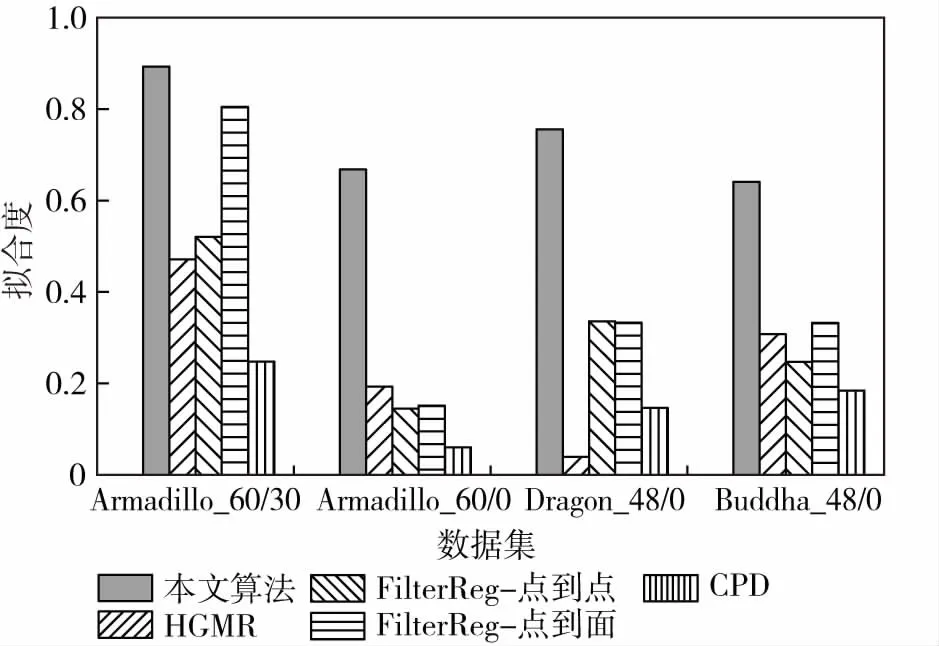
图3 不同算法拟合度比较

4.2 真实数据评估

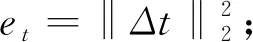
用A、B、C和D表示Livingroom1的前五片点云组成的四对配准目标，用E、F和G表示Office2的前四片点云组成的三对配准目标。表2列出了各配准目标的原始点数和下采样后的点数，以及本文算法推测出的对应位置缺失比率M和外点比率ω.图4(a)展示了配准目标A、D和G 的初始对齐，其中源点云和目标点云分别被标记为红色和蓝色；图4(b)是用本文方法得到的最终对齐，可见本文方法有较好的配准结果。

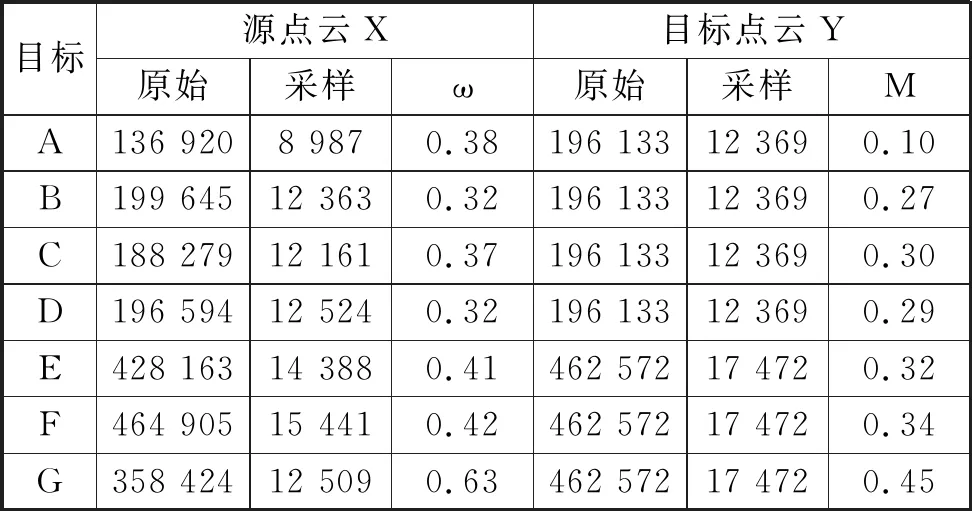
表2 配准目标的数据描述

图4 A、D和G的配准结果

CPD和HGMR不适合在CPU上处理点数过万的点云，因此本文与点到面FilterReg[5]和Open3D中的点到面ICP进行比较。表3和表4分别是不同方法在不同配准目标上的旋转误差和平移误差。本文方法在A、B、C和D上旋转误差较低，在A和D上平移误差较低。FilterReg在E、F和 G上变换误差较低，在A上配准失败。ICP算法配准结果不理想且在 A、 B和G上配准失败。可以看出本文算法在A、B、C和D上的变换误差相对较低，在E、F和 G上的变换误差高于FilterReg，主要原因是配准目标E、F和 G的对应位置缺失比率和外点比率较大，本文算法产生退化。

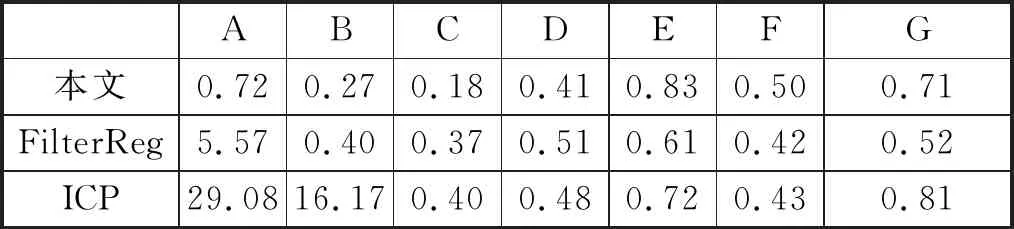
表3 不同算法的旋转误差(°)

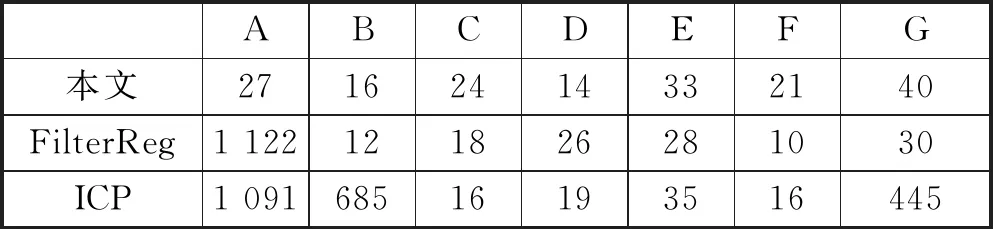
表4 不同算法的平移误差(mm)

图5是不同配准目标在最大对应距离设置为10 mm时，不同算法的拟合度。本文方法与其他方法相比，具有较高的拟合度，配准精度较高的，更好的应对了不同程度的对应位置缺失和外点。

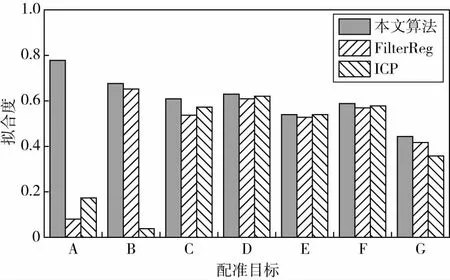
图5 不同算法拟合度比较

5 结论

本文提出了一种结合点到面距离和先验概率加权的点云配准方法。首先，使用先验概率重新加权GMM各分量并以此处理对应位置缺失；其次，使用后验概率推测潜在外点及其比率；然后，用点到面距离衡量点云之间相似性，更好地配准了平面结构较多的点云；最后，在求解GMM参数时删除潜在外点提高算法准确性。实验和评估结果表明，本文配准方法能有效处理点云中的外点、对应位置缺失和平面结构。