基于Hermite多项式函数链模糊神经网络的PMLSM分数阶反推控制

赵希梅， 王天鹤

(沈阳工业大学 电气工程学院，辽宁 沈阳 110870)

0 引 言

与传统的旋转电机相比，永磁直线同步电动机(permanent magnet linear synchronous motor，PMLSM)将旋转运动转化为直线运动，省去了中间机械传动变换装置，有效降低了机械损耗、齿侧间隙等缺点,在实际应用中提高了系统的定位精度[1-2]。但由于PMLSM固有的机械结构，使系统中存在的参数变化和外部扰动等不确定性因素直接作用在电机动子上，影响了伺服系统的控制性能[3]。因此，为满足高精度位置控制的要求，必须在控制系统设计中有效地解决这些问题。

反推控制是一种强鲁棒性的非线性控制方法，能够利用Lyapunov稳定性理论对高阶系统的每一阶子系统设计虚拟控制律，从而实现全局调节和跟踪[4]。但反推控制需要系统精确的动态模型，参数变化和外部扰动都可能导致系统不稳定。因此，为减小不确定性对系统造成的影响，可以将反推控制中加入自适应，使反推控制具有自适应规律，以获得良好的自适应控制性能[5]。对于复杂的控制系统模型而言，传统的反推控制采用的整数阶运算不一定能使系统获得最佳性能[6]。文献[7]采用了分数阶反推控制(fractional-order backstepping control，FOBC)方案，与整数阶运算相比，分数阶运算具有更高的自由度，能实现更好的性能。文献[8]将FOBC用于非线性系统中，能够减弱不确定性和外部扰动对系统的影响，无论初始状态如何，系统都能借助FOBC在有限时间内收敛，达到更好的控制目的。虽然FOBC能够减小不确定性对系统造成的影响，但由于其使用了单一的自适应律，自适应效果较差。因此，可采用神经网络在线估计不确定性，由于将多个自适应律相结合，系统的收敛速度也随之提高。函数链模糊神经网络(functional link fuzzy neural network，FLFNN)将函数链神经网络与模糊规则相结合，与传统的模糊神经网络相比，可以加快收敛速度并降低计算复杂度[9-10]。

为了更加有效地控制PMLSM伺服系统，本文采用了FLFNN与FOBC相结合的控制方案。FOBC在传统反推控制的基础上加入了分数阶运算，减弱了不确定性对系统的影响；同时采用FLFNN对系统中存在的不确定性进行估计，且将易于计算、具有强大逼近能力的Hermite函数作为其扩展函数，改善了FLFNN的建模性能和学习效率，提高了PMLSM控制系统的鲁棒性。但由于估计误差不可避免，因此采用指数补偿器对估计误差进行补偿，该补偿器的控制增益能够随跟踪性能而改变。最后，通过实验验证了该方法的有效性。

1 PMLSM数学模型

PMLSM的电磁推力方程为

(1)

式中：Fe为电磁推力；τ为极距；λd、λq，id、iq，Ld、Lq分别为d、q轴的磁链、电流和电感；λPM为磁链。

由式(1)可知，若id=0，则Fe仅与iq成正比，那么通过控制iq就可使推力达到最大，因此PMLSM的电磁推力可简化为

(2)

式中：kf为电磁推力系数。

PMLSM的运动方程为

(3)

将式(3)改写为

f+gu+d。

(4)

通常，系统的不确定性会使参数f和g发生变化，而外部扰动会对动子的位置x造成影响。因此，在存在参数变化和外部扰动时，式(4)改为

fn+gnu+Ω。

(5)

式中：Δf和Δg为建模误差和参数变化；Ω=Δf+Δgu+d为总的不确定性且|Ω|≤ρ，ρ为正常数。一般来说，由于老化、磨损和操作条件的变化，PMLSM的不确定性很难精确得到。因此，本文的目的是设计一个高性能的控制系统，使动子在存在不确定性的情况下准确地跟踪位置指令。

2 PMLSM系统的设计

PMLSM伺服系统框图如图1所示。通过直线光栅尺检测动子位置，位置控制器采用基于HFLFNN的FOBC方法，其输入为位置跟踪误差ec，输出为q轴电流；通过电流传感器检测三相初级绕组电流ia、ib和ic，经过Clarke变换和Park变换转换为旋转坐标系中的直流分量id和iq作为电流环的负反馈量，电流控制器采用PI控制。

图1 PMLSM伺服系统框图Fig.1 Block diagram of PMLSM servo system

2.1 反推控制系统设计

PMLSM伺服系统的控制目的是使动子的位置x渐近地跟踪参考轨迹xd。步骤如下：

第一步：定义跟踪误差ec=xd-x，然后定义虚拟稳定函数为

(6)

式中kB1为正常数。定义虚拟跟踪误差为

(7)

(8)

(9)

(10)

(11)

式中：kB2为常数；sgn(·)为符号函数。将式(11)代入式(10)得

(12)

2.2 分数阶反推控制系统设计

为提高基于反推控制的PMLSM伺服系统的跟踪性能，提出了一种基于分数阶虚拟稳定函数的FOBC方法，可以有效地提高系统的瞬态和稳态响应。首先，选择分数阶虚拟稳定函数为

(13)

式中：kFB1、c1和c2为正常数；α和β为分数阶的导数和积分的阶数。然后，定义虚拟跟踪误差为

c1Dαec+c2D-βec。

(14)

对式(14)求导得

(15)

c2ecD-βec)+ρsgn(eFB)]。

(16)

式中：当eFB>0，eFB=0和eFB<0时，sgn(·)的值分别为1,0和-1，则式(5)描述的控制系统是渐近稳定的。

为保证FOBC系统的稳定性，将式(13)、式(14)代入式(9)得

ec(φFB-kFB1ec-c1Dαec-

c2ecD-βec。

(17)

fn-gnu-Ω)。

(18)

若FOBC采用式(16)中控制律，则

ρ|eFB|-eFBΩ≤

|eFB|ρ+|eFB||Ω|≤-

|eFB|(ρ-|Ω|)≤0。

(19)

2.3 基于HFLFNN的不确定性估计器的设计

由于Hermite多项式具有独特的逼近能力，因此选择式(20)所示的多项式作为输入变量构成HFLFNN[11]。其结构如图2所示。

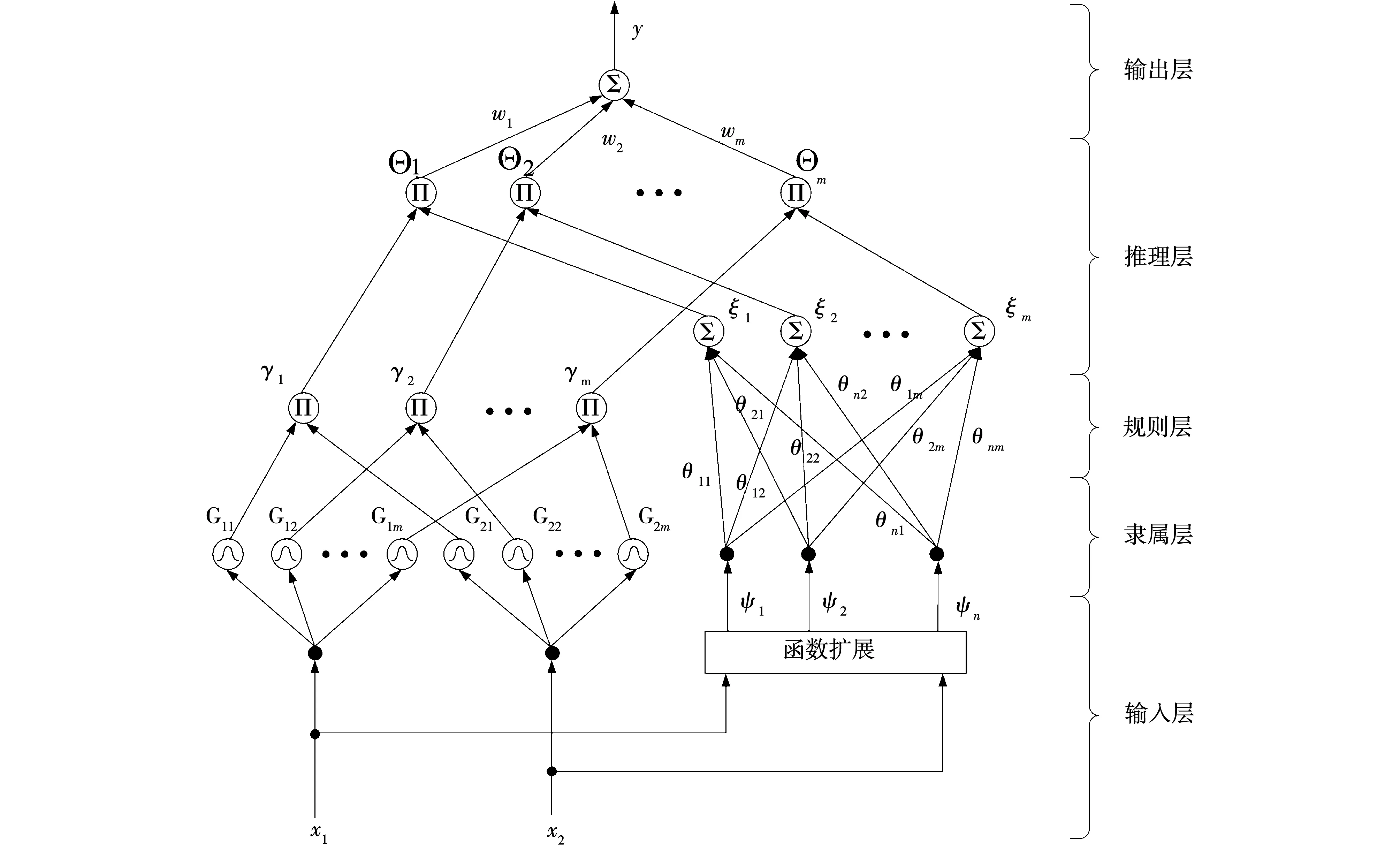
图2 HFLFNN的结构框图Fig.2 Structure diagram of HFLFNN

(20)

式中：ψk为正交Hermite多项式函数；n为扩展函数的数量。此外，正交Hermite多项式由H1(xi)=1，H2(xi)=2xi，…，Hk(xi)=2tHk-1(xi)-2(k-1)，Hk-2(xi)，k≥3。因此对于输入向量X=[x1,x2]T，输入向量可以扩展到增强空间，如ψ=[ψ1,ψ2,…,ψn]T=[ψ1(x1),ψ2(x1),…,ψn/2(x1),ψ1(x2),ψ2(x2),…,ψn/2(x2)]。

第2层(隶属层)中的每个节点采用高斯函数充当隶属函数

(21)

式中：cij和σij分别是高斯函数的均值和标准差；m表示该层中的节点数。

第3层(规则层)中的节点将第2层的输入信号相乘

(22)

式中γj是第j个模糊规则的激活函数及第3层的输出。网络的输出由第j个节点的线性和来表示

(23)

式中：θkj为连接权重；ξi为函数扩展的输出。

第4层(推理层)中的节点将来自第3层的输出γj和来自网络的输出ξi相乘，即

(24)

推理层中每个节点的模糊规则j为：若x1为A1j，x2为A2j，则

(25)

第5层(输出层)中的每个节点对应于单个输出量且充当解模糊器，即

(26)

式中：wj为第4层和第5层的连接权重；y为HFLFNN的输出；参数w，c，σ和θ定义为w=[w1...wm]T∈Rm×1，Θ=[Θ1…Θm]T∈Rm×1，c=[c11…c1m,c21…c2m]T∈R2m×1，σ=[σ11…σ1m,σ21…σ2m]T∈R2m×1和θ=[θ11…θ1m,θ21…θ2m,θn1…θnm]T∈Rnm×1。

由于通用函数逼近特性，存在理想HFLFNN不确定性估计器，其输出可以均匀地近似不确定性为

Ω=y*+Δ=W*TΘ(c*,σ*,θ*)+Δ=

W*TΘ*+Δ。

(27)

式中：Δ表示由于HFLFNN的有限结构而导致的最小估计误差；W*，Θ*，c*和θ*为W，Θ，c和θ的最优参数向量。但确定最优估计下的最优向量几乎不可能，因此采用了HFLFNN来实现估计，即

(28)

(29)

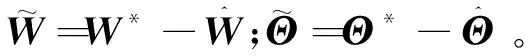
(30)

2.4 在线不确定性估计的补偿和参数调整

为了更加有效地估计不确定性，采用指数补偿器平滑地补偿HFLFNN的估计误差。同时，为保证系统的稳定性，推导自适应估计律。将式(27)代入式(15)得

(31)

系统的雅克比矩阵可改写为∂V2/∂uE=-e2。计算误差项

(32)

基于HFLFNN的FOBC总控制律uIFB=u为

uIFB=uFB+uEC，

(33)

(34)

(35)

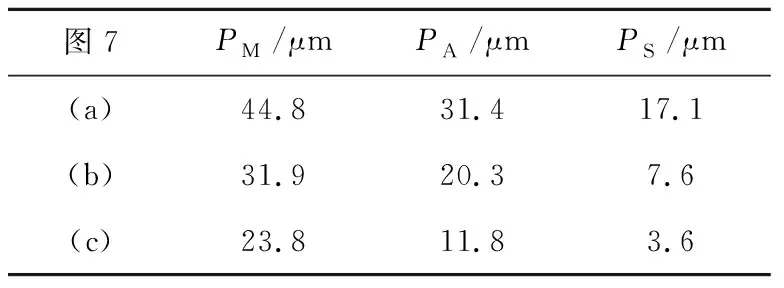
式中：q满足条件0

(36)

式中：ηw，ηc，ησ和ηθ为正的学习律，保证了PMLSM控制系统的渐近稳定性。基于HFLFNN的FOBC结构框图如图3所示。

图3 基于HFLFNN的FOBC系统框图Fig.3 Structure diagram of FOBC based on HFLFNN

3 系统仿真与实验分析

为验证所提方法的有效性，采用MATLAB/Simulink仿真软件与DSP实验平台对基于HFLFNN的FOBC系统进行了仿真与实验研究。选取PMLSM的主要参数为M=16.4 kg，B=8.0 N·s/m，τ=16 mm，kf=50 N/A，基于HFLFNN的FOBC系统的参数为：kB1=15.5，kB2=0.05，ρ=0.01，kFB1=15，kFB2=0.03，c1=0.03，c2=0.01，α=0.4，β=0.3，ηw=0.03，ηc=0.001，ησ=0.01，ηθ=0.01，q=0.4，E=0.1，r=0.05。所有控制器参数在选取时均经过多次仿真与实验试凑调整，以保证系统具有最佳的稳态和动态性能。

在图4(a)所示的梯形位置输入信号下，对系统施加如图4(b)所示的变负载条件。反推控制、FOBC和基于HFLFNN的FOBC的PMLSM系统的位置跟踪误差曲线分别如图5(a)、5(b)、5(c)所示。为便于控制器性能的比较与分析，选取仿真和实验结果的最大跟踪误差PM、平均跟踪误差PA和跟踪误差的标准差PS作为性能指标。表1为三种控制方法仿真结果的性能指标。

图4 位置输入信号和负载曲线Fig.4 Position input signal and load curves

图5 梯形输入信号下位置跟踪误差曲线(仿真结果)Fig.5 Position tracking error curves of trapezoidal input signal (simulation results)

表1 跟踪性能指标

在相同的位置输入信号与变负载条件下，对PMLSM系统进行了实验研究。实验时采用DSP TMS320F2812A作为执行单元，基于DSP的PMLSM控制系统结构图如图6所示，主要包括PWM逆变器，PMLSM、直线光栅尺、电流传感器和DSP控制单元等。三种控制方法下的位置跟踪误差曲线分别如图7(a)、7(b)、7(c)所示，对应的实验结果性能指标如表2所示。

图6 基于DSP的PMLSM控制系统结构图Fig.6 Structure diagram of PMLSM control system based on DSP

图7 梯形输入信号下位置跟踪误差曲线(实验结果)Fig.7 Position tracking error curves of trapezoidal input signal (experimental results)

表2 跟踪性能指标

对比图5和图7的位置跟踪误差曲线可以看出，不管是仿真结果还是实验结果，三种方法在梯形信号的转折处和负载突变处都存在误差，但所提出的基于HFLFNN的FOBC方法控制下的位置跟踪误差曲线更为平滑，波动更小。对比表1和表2可以看出，相比于仿真结果，实验结果效果稍差，但所提方法的跟踪误差的PM、PA和PS性能指标都明显优于反推控制和FOBC方法，取得了较高的位置跟踪精度。因此，无论在转折处还是负载变化时，基于HFLFNN的FOBC都具有更小的误差和更好的稳态性能。

为实现PMLSM的变速运动，给定正弦输入信号如图8所示，反推控制、FOBC和基于HFLFNN的FOBC的PMLSM伺服系统的位置跟踪误差曲线分别如图9(a)、图9(b)和图9(c)所示，三种控制方案对应的性能指标如表3所示。从跟踪误差曲线波形图可明显看出，图9(a)的误差曲线波动幅度最大，图9(c)的误差曲线最平稳。对比表3也可以看出，基于HFLFNN的FOBC控制方法在变速运动时仍能保证较好的位置跟踪性能，最大跟踪误差及平均误差明显小于另外两种方法，且跟踪误差的离散程度更小。因此，通过实验可知，基于HFLFNN的FOBC方案显著提高了系统的控制精度和鲁棒性能。

图8 正弦位置输入信号Fig.8 Sinusoidal position input signal

图9 正弦输入信号下位置跟踪误差曲线(实验结果)Fig.9 Position tracking error curves of sinusoidal input signal (experimental results)

表3 跟踪性能指标

4 结 论

针对PMLSM伺服系统位置跟踪精度问题，采用基于HFLFNN的PMLSM分数阶反推控制方案。利用FOBC减小了系统的稳态误差；为进一步提高FOBC下的PMLSM系统的定位精度和鲁棒性，设计了包含HFLFNN不确定性估计器和指数补偿器在内的FLFNN分数阶反推控制，FLFNN通过在线学习估计系统中存在的不确定性，指数补偿器通过平滑指数自调节机制来补偿估计误差；最后通过Lyapunov函数推导出基于HLFNN的FOBC的自适应估计律。实验结果验证了所提出的控制方法具有更好的控制性能。