一种三相交错并联双向传输CLLLC谐振变换器

杨玉岗， 侯博译， 付兴武， 李恒

(辽宁工程技术大学 电气与控制工程学院，辽宁 葫芦岛 125105)

0 引 言

当前，随着社会信息化、智能化的不断发展，在电动汽车、新能源发电、直流配电系统、个人移动设备等领域，对DC/DC变换器的效率、容量和体积等性能指标的需求越来越高，尤其是当前重点发展的电动新能源汽车领域，对大功率隔离型双向DC/DC变换器有着多方面高标准的性能需求，要求同时具有直流调压、双向功率传输和电气隔离的功能等，然而，如何同时实现在宽输入、输出范围内保持高效率、高功率密度、大容量，是大量研究人员探索的重要方向[1-4]。

谐振型软开关DC/DC变换器成为了研究的焦点已久，其中LLC谐振变换器凭借其在宽输入范围、全负载范围内，自然实现原边开关零电压开关的零电压开通(zero voltage switching，ZVS)和副边整流二极管的零电流开通(zero current switching ，ZCS)的优良的特性，一直得到极大的关注。特别是在对效率、功率密度和电磁兼容性都有严格要求的场合。其软开关特性保证了在更高的频率下操作也能够保证很高的效率，有效地缩减了元件的尺寸，实现高功率密度[5-7]。然而，LLC谐振变换器只具备在正向功率传输时保持软开关特性，对此已有文献基于LLC结构的基础上探究了双向软开关的功率传输结构。文献[8]研究一种对称结构CLLC型谐振变换器，正反向工作特性相同，但输出侧的谐振电路会消耗功率，文献[9]研究了CLLC谐振变换器，其正反工作特性不同，但只有在正向工作时原边ZVS、副边ZCS，反向工作时只能实现原边开关管ZVS。文献[10]研究了一种对称结构的CLLLC型拓扑，能够同时在正、反向都具备LLC谐振变换器的软开关特性，也同样无需缓冲电路，但是其并没有提出在应对较宽的输入输出增益的方案，最高增益仅为一点零几。

在扩大单机容量上，三相交错并联结构相比半桥和全桥结构在高功率水平上有多种优势。三相结构可以获得更好的损耗分布，更容易的热管理，更低的输入和输出电流纹波，以及较小的尺寸的主动和无源元件和散热器。由于这些特点，功率水平可以增加到几千瓦，因此三相交错并联方案为众多研究人员重点研究[11-14]。

本文在前人的基础上提出了一种新颖的三相Y-Δ型交错并联结构的双向功率传输CLLLC型DC/DC谐振变换器。它在结构上兼顾了多项交错并联结构的大容量和CLLLC结构的双向功率传输能力，同时有变压器变比小和相间自动均流的优势；在谐振电路的工作特性上可以实现一定范围的增益放大，而且变换器在正反向工作都具有类似LLC的软开关特性。本文首先描述了三相CLLLC谐振变换器的工作过程，而后使用基波分析法(first harmonic approximation,FHA)分析其在高低压侧谐振腔不完全对称情况下，对比分析参数变化对增益在不同频率以及不同负载下的影响。在了解其特性后根据所需的增益变化范围来限定参数，而后使用软开关条件进一步限制参数，选取满足要求的参数。最后，试制一台1.5 kW的样机，验证结构和设计的可行性和有效性。

1 三相Y-Δ接CLLLC拓扑原理

本文研究的三相Y-Δ型交错双向CLLLC谐振变换器的拓扑结构如图1所示，整体分为五部分，分别为：高压侧三相桥、高压侧Y型连接部分、CLLLC谐振电路、低压侧△形连接部分和低压侧三相桥。

图1 三相Y-Δ型交错双向CLLLC谐振变换器Fig.1 Three-phase Y-Δ type interleaved bidirectional CLLLC resonant converter

根据功率流向的不同，将谐振变换器分为正向反向两种工作状态。两侧三相桥臂的控制波形如图2中所示，各相的导通控制信号相差120°的相角，每个桥臂的上下管的驱动信号相互补，各占50%。 其中一个桥臂工作在正半周期时，另外两相桥臂共同作用，一起作为其负半桥来配合工作，即可用三个桥臂产生类似三对全桥的效果，相比于3套独立完整的全桥，大量减少开关管的数量。

图2 三相桥的驱动信号Fig.2 Driving signal of three phase bridge

此三相谐振变换器每一相都拥有一个完整的CLLLC结构，各自包含原边谐振电感、谐振电容、变压器(包含受气隙控制的励磁电感)、低压侧谐振电感和谐振电容。高压侧三相间以Y型接法相连，低压侧以D型接法相连。

在分析高压侧各谐振腔端口的电压(AN、BN、CN)时，要首先分析高压侧中性点N的电位。谐振变换器工作在正常频率下，开关频率较为接近高低压侧谐振腔的谐振频率，即谐振电感和谐振电容处于谐振或近似谐振的状态，不会分压，所以N点电位直接受三相桥臂开关影响，如忽略死区时间，则呈现两种状态，如图2中N点电压所示。在高压侧输入、低压侧输出状态，则呈现：①ABC三桥臂中两相输入高电平、一相低电平，N点表现为高电平状态；②ABC中一相输入高电平、两相输入低电平而形成的低电平。若为低压侧输入，高压侧输出，则ABC三相桥臂会使高压侧谐振腔端口被输出滤波电容的电压钳位，也会同样形成高电平和低电平两种状态。

基于N点的高低电平状态，与ABC点受各相桥臂的开关所导通形成的电位，即可在AN、BN、CN间形成如图3中所示的输入输出电压。

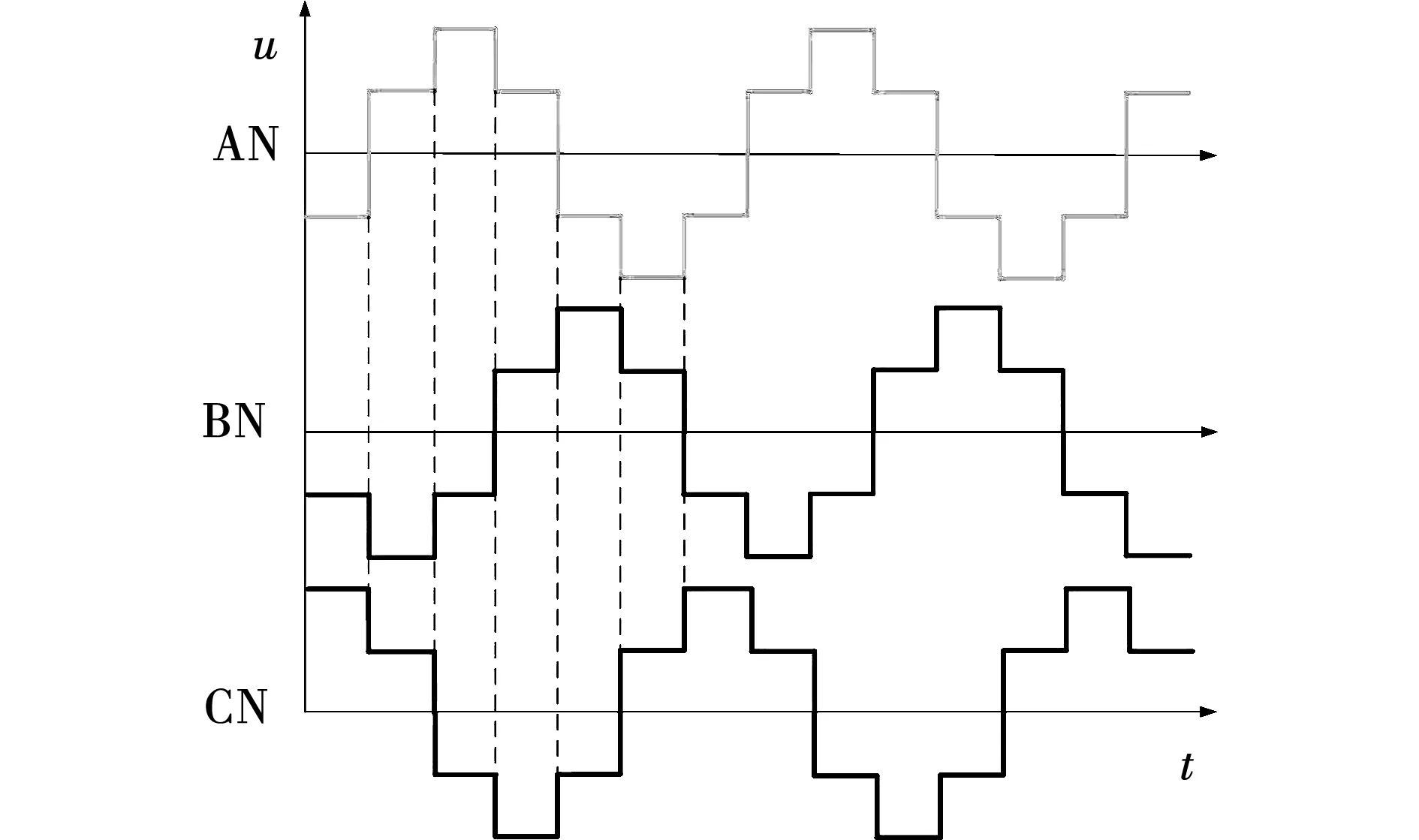
图3 高压侧Y接三相桥输入或输出电压波形Fig.3 Input or output voltage waveforms of Y-connected three-phase bridge

而分析低压侧各谐振腔端口的电压(ab、bc、ca)时，a、b、c三点的电位也同A、B、C三点一样，在输入状态时被电源bus电压钳位为高电平或低电平，在输出状态时被滤波电容电压钳位。所以再关联ab、bc、ca之间，即可得到如图4中的电压曲线。

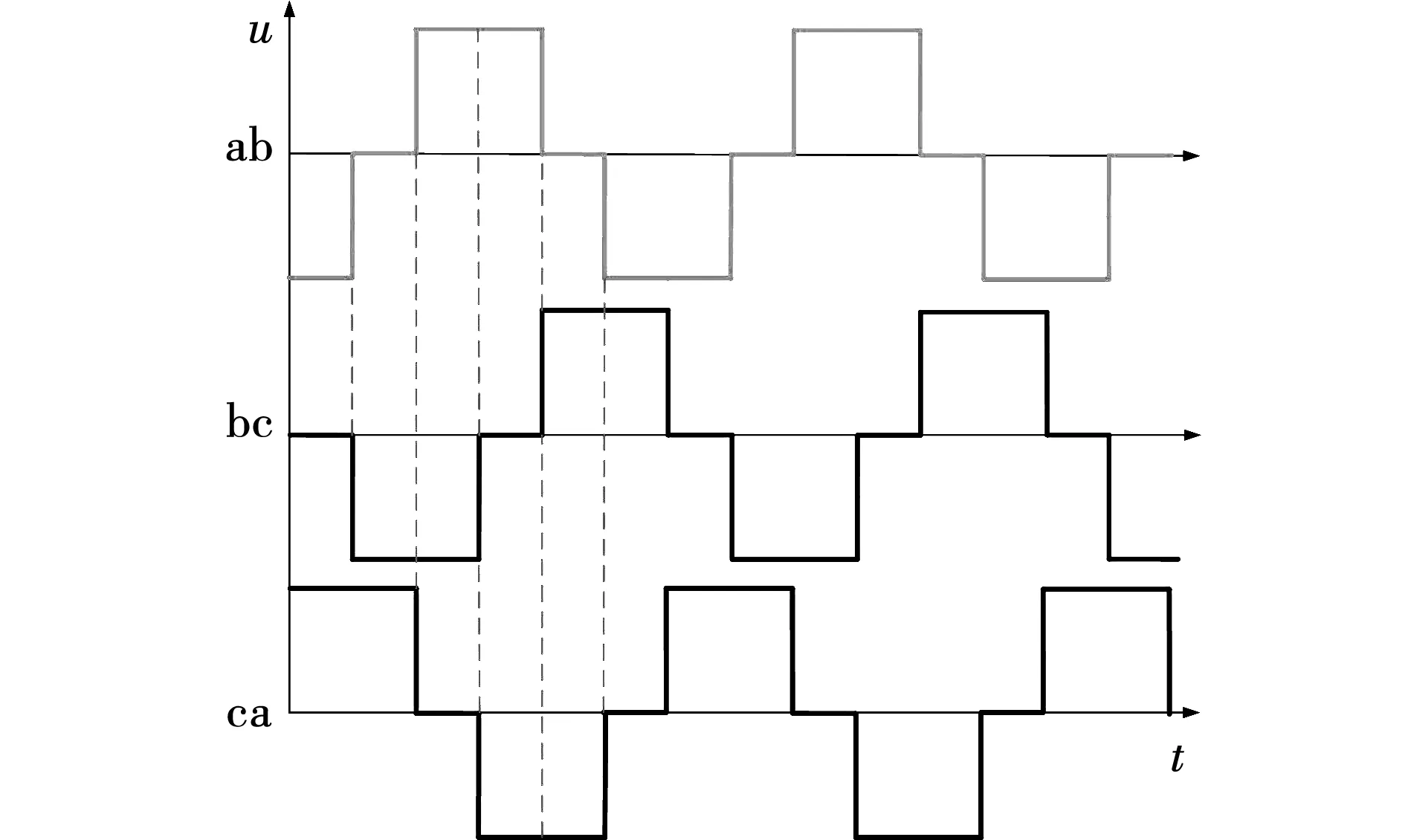
图4 低压侧Δ接三相桥输入或输出电压波形Fig.4 Input or output voltage waveform of Δ-connected three-phase bridge

在分析模态时，三相CLLLC谐振变换器的低压侧结构上需要从Y-Δ结构等效变换为Y-Y型结构，参数上低压侧电感和电容的参数都需要做等效变换，再拆分为3个独立的桥臂，来单独分析各相的工作过程。

单独分析其中，可将单个桥臂的一个周期分为12个工作状态，正负半周各6个，副半周期的工作状态与正半周相似，不再赘述，对正半周期6个工作状态具体情况分析如下：

1)工作状态1:T0时刻开始，Q14关断进入死区时间，Lm1中的电流自其他两相谐振电路通过Cr1流入，反向通过Lm1，一部分通过变压器继续向负载侧输送，其余电流经过Lr1给高压侧开关管的寄生电容充电，开关管Q11的Vds开始降低，Q14的Vds开始升高。

图5 A相fm

2)工作状态2:T1时刻,Q11的Vds达到体二极管开通所需电压时，体二极管D11导通，此状态下开关管源极电压要高于漏极，可以实现Q11的ZVS(zero voltage switching)。

3)工作状态3:T2时刻,驱动Q11开通，Lr1中流过的反向电流迅速减小，但继续给电容C14充电。

4)工作状态4:T3时刻,iLr1减小到0并在电源输入电压的推动下电流开始正向流动。iLm1持续减小，高压侧电流经过Cr1流向其他两相谐振电路，低压侧流向负载侧的iLr11继续增大。

图6 工作状态Fig.6 Working type

5)工作状态5:T4时刻，Lm1中的电流减小到0，并开始正向流动开始增大，经过理想变压器流向另两相谐振电路的电流和iLr11达到最大点并开始减小。

6)工作状态6:T5时刻，iLr1和iLm1大小相同，流经变压器的电流减小为0，而后因为低压侧Lr11的存在，变压器电压不会被输出电压钳位，Lr11开始产生反向的电流流经变压器，低压侧电流经过Cr11流入另外两桥臂，变压器高压侧的电流会和iLr1一起流入Lm1,经过Cr1，流入另两相谐振电路。

2 CLLLC谐振变换器参数分析

2.1 负载等效阻抗

本文使用基波分析法来分析CLLLC谐振变换器，其基波等效电路如图7所示。RL为输出载荷，Req是负载交流等效负载，Rac为等效到高压侧的交流等效负载，将低压侧等效到高压侧。

图7 CLLLC谐振变换器Fig.7 CLLLC resonant converter

Io为三相总输出电流平均值，Irms为单相输出电流有效值，Ipeak为单相输出电流峰值。

(1)

(2)

Vo为输出电压平均值，Vo.FHA为单相输出电压基波有效值。根据正弦波形积分得

(3)

输出电压有效值为

(4)

负载的等效阻抗可由Vrms和Irms之比可得，代入式(2)、式(4)得

(5)

正向传输时，将交流等效阻抗都折算到高压侧时，可表示为

(6)

因为反向传输时负载位于高压侧，负载的等效阻抗值在向高压侧折算时，不用放大n2倍，其值为

(7)

2.2 正向传输增益

设谐振电感和励磁电感的比值为

k=Lm/L1。

(8)

高、低压侧的谐振电感比为

h=L2/L1。

(9)

高、低压侧谐振电容比为

g=C2/C1。

(10)

高压侧谐振频率为

(11)

低压侧谐振频率为

(12)

谐振点角频率为ωs，归一化频率为

(13)

正向品质因数为

(14)

参考在文献[10]中对CLLLC谐振变换器对正向传输增援的研究，正向增益Gac表示为

(15)

展开整理为

Gac=

(16)

其中:

a=k+hk+h，

(17)

(18)

(19)

2.3 反向传输增益

为了保证高、低压侧两个谐振腔工作在相同的频率下，即ω1=ω2，可得

hg=1，

(20)

(21)

(22)

再令：

(23)

(24)

z=g。

(25)

设定反向品质因数:

(26)

反向增益表达式为

Gback=

(27)

代入式(15)，展开可得反向增益Gback的表达式为

(28)

2.4 参数对增益特性的影响

为了探究在hg=1的前提下，分析k、g与h三个参数变化对增益的具体影响，使用MATLAB画出三维视图辅助分析。首先，画出h、g不变(取h=g=1)k取不同值下，ωn与Q对增益G的曲面图，如图8所示。从图8中红色箭头所指出的高增益区域在XY平面上投影的位置可见，高增益区域随k增大向ωn轴的原点推移，即想要达到高增益需要更大的变频幅度；同时波形下沉，取相同Q值能够取得的增益变小，取得较高增益的Q值范围缩小，尖峰越细；无论k值如何变化，在归一化频率点ωn=1上，Gback始终为1。

图8 k的变化对增益G的影响的对比图Fig.8 Contrast diagram of the effect of k change on gain G

从图9中可见，在k值固定为10时，h变化对增益G关于Q和ωn的变化情况，取相同Q值时(如Q=1),随着h增大,波形在会ωn=1处会越加尖锐，增益在趋近该处的变化会越明显；相对的h越小，波形越圆润，增益变化越平滑。此外，Q越小，h、g的变化对增益的影响越小，至Q=0时增益为相同的曲线。

图9 h的变化对于增益G的影响的对比图Fig.9 Contrast diagram of the effect of h change on gain G

3 参数选取

3.1 选取参数的关键

在选取参数时，要根据所需要的具体情况来挑选合适的参数，以满足在该条件下所需的输入输出特性。本文以反向传输时达到特定放大增益范围为假设目标条件进行设计，其最大增益用Gmax表示。从图8、图9中增益的图形可知，在归一化频率点的增益必定为1，所以选取一个可以达到所需最高增益点的参数关系，就能通过变频达到增益从1到Gmax的范围内输出。

3.2 谐振参数关系选取

将目标的最大增益Gmax代入式(28)中替换Gback，得

Q2=

(29)

为了相对地提高谐振变换器的效率，Lm取值应该尽量大，以减小励磁电感电流和减小关断电流。

由式(15)和式(20)可知，令：

M=k2Q2=kgQ2=

(30)

可见Lm的取值由k、g、Q2决定,即M值的大小直接反应Lm的大小。

用MATLAB分别画出ωn=0.1～0.9时，k、g的取值对Q2、M的三维曲面，分别对比其中Q2、M的值，其中ωn越大，Q值所能取得的峰值整体越小， 所能取得的峰值整体越小，以此选取出适当的ωn，举例如图10(a)、10(b)中所示的ωn=0.5的情况，其他不再一一列举。为了防止波形过于畸变，要保证ωn的值不能过小，ωn过大也不利于使用变频来控制输出增益。

图10 ωn =0.5时Q、M的曲面图Fig.10 Surface graphs of Q & M at ωn=0.5

由此经效率等因素权衡后选取得ωn，进而在图中根据选取的Q就可以得到k、g，以图11中情况为例，选取了k=13，g=0.14点。

图11 ωn=0.667ωn=0.667时Q值的曲面图Fig.11 Surface graphs of Q & M at ωn=0.667 ωn=0.667

进一步由式(29)得：

(31)

代入f,可以得到可以满足增益的Lm的一个极大值。

为了保证励磁电感电流的大小足以实现ZVS，励磁电感还有一个最大限度：

(32)

其中：Tmin为各频率下谐振周期的最小值；Tdead为死区时间；Cs为电路的寄生电容与开关管寄生电容的总和。

3.3 谐振电感和谐振电容的选取

谐振电感和谐振电容共同组成谐振腔保证能量在变压器里的传输。要确定高压侧电感的大小，可及由上小节所得的最大励磁电感的大小以及高压侧谐振励磁电感和谐振电感的比值k来取得：

(33)

在确定好谐振频率后，可求得高压侧谐振电容

(34)

低压侧的谐振电感值为

(35)

低压侧的谐振电容：

Cr11=n2C2=n2gCr1。

(36)

4 实验验证

为了验证本拓扑结构的可行性，设定其应用于高压侧400 V直流母线和低压侧24～48 V蓄电池之间的功率传输。以此为目标制作一台容量1.5 kW的样机进行验证，样机平台如图12所示。

图12 1 500 W三相Y-Δ型交错并联双向CLLLC谐振变换器实验样机Fig.12 Experimental prototype of 1 500 W three-phase Y-Δ type interleaved bidirectional CLLLC resonant converter

当谐振变换器正向工作时，由400 V直流母线输入，向低压侧的蓄电池输出48 V充电，工作条件和参数如表1所示。此状态下，变换器工作在额定频率点ωn=1附近，增益基本不随负载变化而变，如果电压略微偏高，可以通过小幅提高频率来降压。

表1 正向工作参数

反向工作时，能量从低压侧蓄电池中向直流母线传输，谐振变换器的工作条件和参数如表2。

表2 反向工作参数

此时，变换器根据输出电压的大小来调整频率，当48 V输入时，工作在额定频率200 k，增益为1，输出约388 V，降频到192 kHz时，增益约为1.04，此时输出可以达到400 V。当输入电压进一步降低时，变换器逐渐降低工作频率，满载时频率在133.3 kHz略高于2倍的增益，实现在24 V输入时输出400 V。

根据表1、2中的参数，使用本文的方法可以解得：

Lm=42.07 μH；Lr1=3.24 μH；Lr11=1.06 μH；Cr1=196 nF；Cr11=596 nF。

基于以上的方法和参数，研制了一台额定功率1 500 W的三相Y-Δ型交错双向CLLLC谐振变换器样机。高压侧使用东芝2SK3934型MOSFET，低压侧使用英飞凌IRF2807型MOSFET。

样机在正反向工作时皆可实现ZVS，如图13中所示。

图13 MOS管的Vds和Vgs波形Fig.13 Vds and Vgs waveforms of MOS transistors

三相Y-Δ型交错并联结构均流效果良好，三相电流基本一致。在各相间参数存在最大±5%差异下，其相间均流效果如图14中所示。

图14 高、低压侧输入时三相谐振电感电流波形Fig.14 Current waveform of three-phase resonant inductor at high and low voltage side input

在图15中给出三相Y-Δ型交错并联结构的传输效率曲线。在正向功率传输测试中拖动额定1 500 W负载的64%时，即输出20 A时得到最高效率，其为93%。

图15 正向传输实验效率曲线Fig.15 Efficiency curve of forward transmission experiment

在测试中确认样机的效率受到了平台中多种寄生参数的影响，而且三相桥中开关管为MOS管，它的导通损耗和关断损耗都比较大，如果采用性能更好的GaN或SiC器件，加入同步整流技术并优化整体布局后会在效率上会有不小提升。

5 结 论

本文提出了一种三相Y-D型交错并联的双向CLLLC谐振变换器的拓扑结构，利用拓扑结构的特性既减小了变压器的匝比，又兼具良好的均流性能。利用基波分析法取得的这种结构变换器的正向、反向增益的表达式，给出一种直观的基于MATLAB的参数选取办法，其中分析了高、低压侧谐振腔参数对增益的影响，此参数设计方法可以作为其他研究者在追求增益范围时的参考；最后基于这种参数选取方法设计了一台样机进行实验验证，证明了本结构相比基本的CLLLC谐振变换器结构，实现了较宽的增益范围并满足大容量需求。尽管本机当前效率并不突出，如果不再考虑成本使用GaN器件并加入同步整流技术，样机效率会有显著的提升。在以后的研究中会进一步具体量化本结构的相间均流效果。