基于自适应PI控制器的直流微电网电压控制策略研究

吴小涛，谭超，王国博

（1.中国船舶重工集团有限公司第七一〇研究所，湖北宜昌 443003；2.三峡大学电气与新能源学院，湖北宜昌 443002；3.北京中电安智科技有限公司，北京 100193）

0 引言

近年来，可再生能源的开发和利用成为各个国家研究的重点，微电网作为新能源发电载体备受关注［1-4］。整流器在交流侧与直流侧之间起着能量传输的作用，并且是微电网系统的控制核心。因此微电网整流器控制策略的研究具有重要意义。

对于单相整流器，其控制目标主要有2个：一是维持恒定的输出电压；二是维持较低的电网电流总谐波失真（THD）。常见的控制方案有滞环电流控制［5-6］、三角波电流控制［7］和电压电流双闭环控制［8-9］等。

对于维持输出电压稳定方面的研究，文献［10-12］通过加入负载电流前馈，来降低电压波动水平，并且使系统的响应速度提高。文献［13］提出一种新的负载电流前馈控制方法，在负载变化过程中提高了系统的动态特性。文献［14-15］通过已知的母线电压和整流器的瞬时功率，利用扰动观测器，将扰动的观测值进行前馈补偿给定值，从而抑制扰动。

对于降低电网电流THD 方面的研究，文献［16-17］提出了基于比例型控制器与电压前馈相结合的电压前馈电流控制方法来降低电网电流THD。文献［18-21］提出了无源去耦技术，即在直流侧使用额外的L 滤波器，增加直流母线电容器或使用电感电容（LC）无源滤波器。文献［22］设计了一种基于比例积分（PI）控制和重复控制双闭环控制策略的并联混合有源滤波器，有效抑制了由非线性负载引起的谐波电流，使电网电流THD满足国家标准。

上述控制方法均针对单个控制目标设计，无法在提升电压稳定性的同时，降低电网电流THD。为了解决上述研究中存在的问题，本文提出了一种基于自适应PI 控制器的直流母线电压控制策略。该策略采用自适应比例和积分增益，在确保提升母线电压稳定性的同时，降低直流微电网反馈给交流电网的电流谐波。

1 建模

1.1 单相交流/直流（AC/DC）建模分析

单相脉冲宽度调制（PWM）整流器拓扑结构如图1 所示。图中ug，ig分别为交流侧电网电压和电网电流；vdc，idc分别为直流母线电压和母线电流；ic是流入电容器C的电流；iload为负载电流。

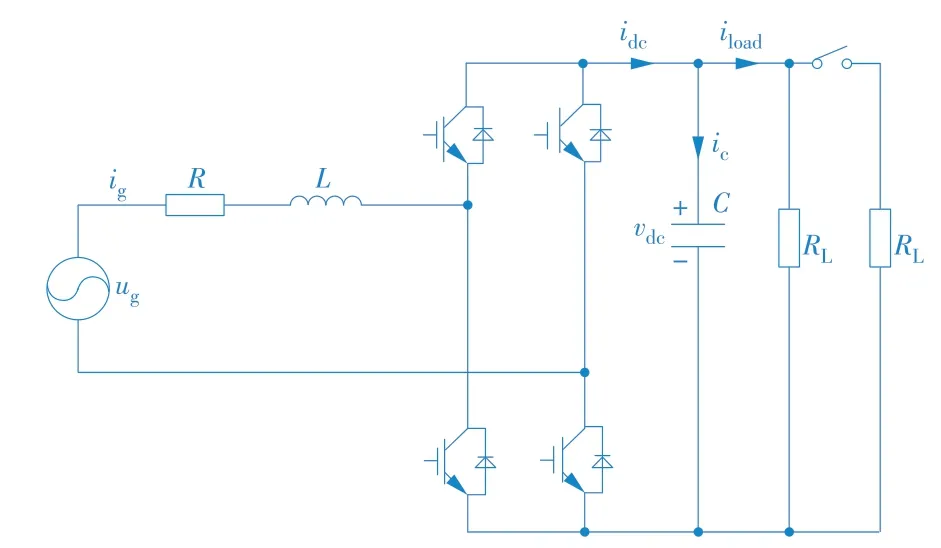
图1 单相PWM整流器拓扑结构Fig.1 Single⁃phase PWM rectifier topology

1.2 模型建立

传统控制方法对不同模式采用不同的建模方法，这虽然提高了模型的精度，但却增加了建模的复杂度，降低了控制效率。相对于传统的电流环控制模型，本文提出了一种用单位增益来代替电流环的控制方法，该方法具有结构简单、适应系统不同状态的特点。

在电流内环达到无静差跟踪后，可将整个环路看做是增益为1 的比例环节。根据瞬时功率平衡，可得

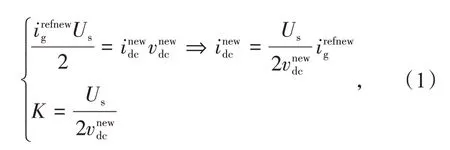
图2 电流内环控制示意Fig.2 Current inner loop control block

本文所提出的自适应电压电流双闭环结构如图3b所示，其电压外环的闭环传递函数可表示为

1.3 控制目标分析

1.3.1 母线电压波动分析

为了得出电压瞬态响应和控制器增益之间的关系，由图3b 可知，从参考电压到母线电压的开环传递函数为

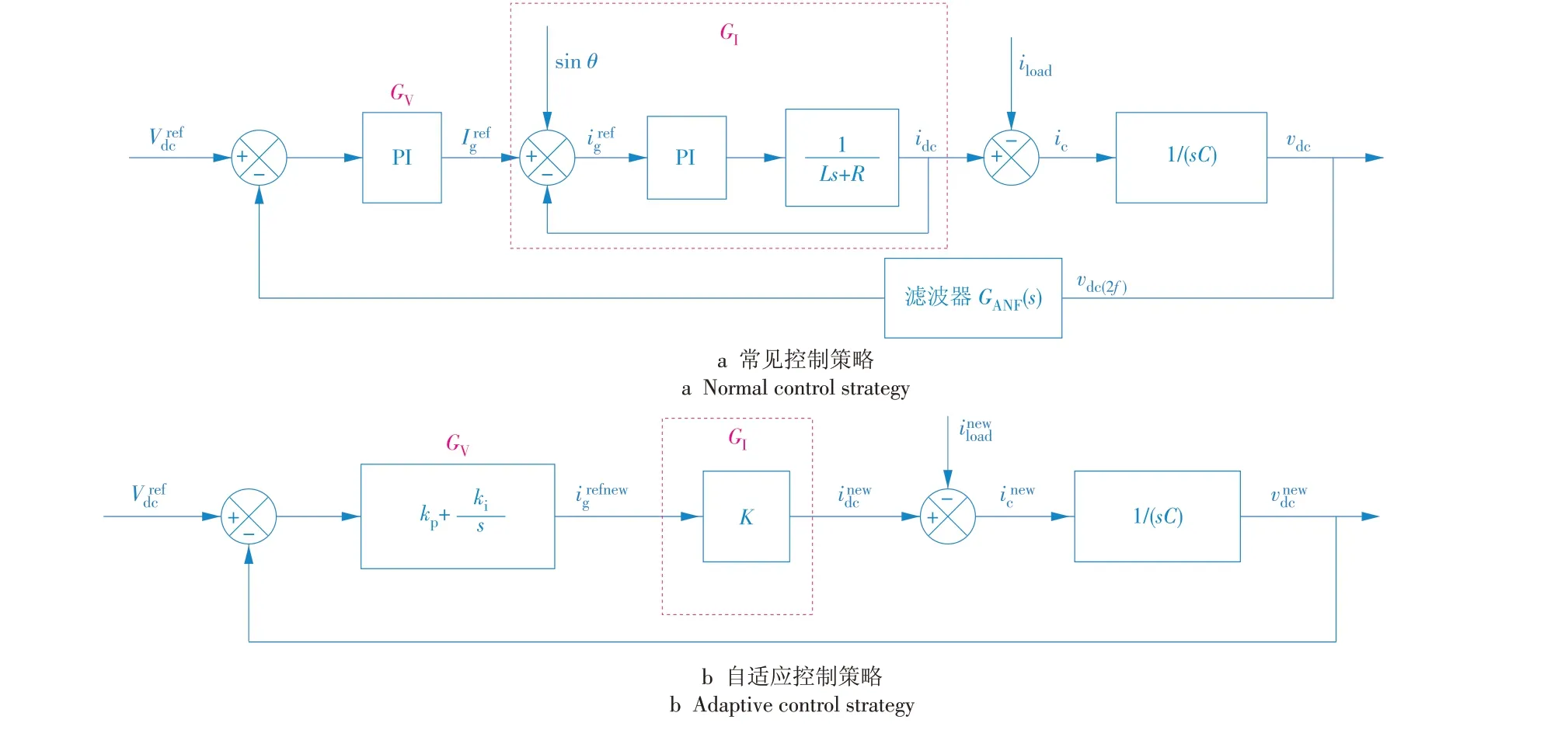
图3 电压电流双闭环控制策略示意Fig.3 Voltage and current double closed⁃loop control strategies

可知两者之间的误差传递函数为

由式（10）可知，峰值波动值Vp的变化与ζ和ωn的变化有关。当ωn增加时，Vp减小；当ζ增加时，Vp增大。

1.3.2 稳态运行期间的二次谐波电流分析

在控制回路中，由于电网电流质量会受到母线电压控制器输出信号中可能存在的低频纹波的影响，所以参考电流上二次谐波的幅度i͂2g可表示为

式中：ω为角频率。

可知，峰值波动Rp值的变化仅与ζ，ωn的变化有关。当ωn增加时，Rp增大；当ζ增加时，Rp减小。

2 自适应PI控制器设计

2.1 自适应PI控制器控制策略

电力转换器连接到电网应遵守“直流母线电压的波动和谐波电流含量要保持在一定范围内”的规定。根据式（10）、式（14）可知，电压波动和电网电流THD 与ωn，ζ有关；由式（4）可知，ωn，ζ可由自适应PI控制器中kp，ki进行调节。

为此本文提出了一种当母线电压波动超过极限之前及时调整电压外环自适应PI 控制器的kp，ki的方法，使其保证最小化电压波动和电网电流谐波。定义直流电路电压波动的参考范围为额定值的±10%，当测量的直流母线电压值超出该频带时，PI增益为常数，否则PI增益为可变值。

本文所提出的自适应PI 控制器的控制策略如图4 所示。由图可知，电压外环的PI 增益（kp，ki）是根据直流母线电压误差的绝对值|Δudc|连续更新。

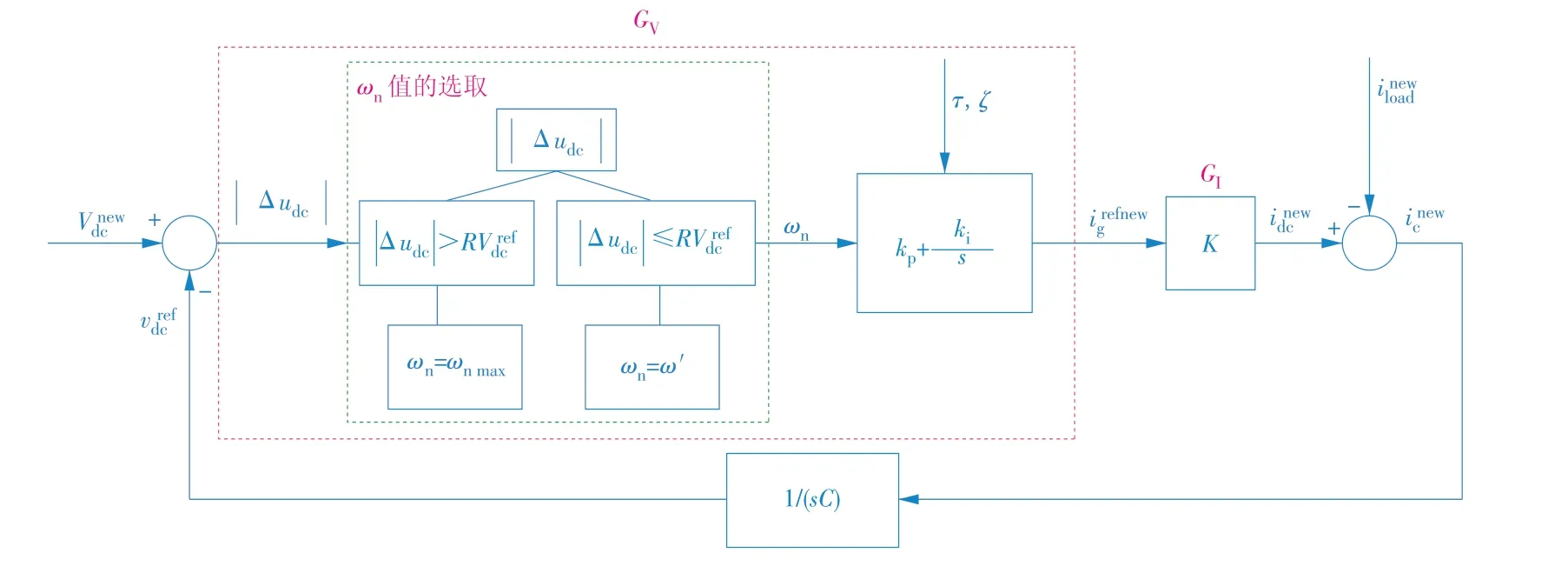
图4 自适应PI控制器的控制策略Fig.4 Control strategy of the adaptive PI controller

ωn值的选择策略如图5 所示。根据图5 在直流母线电压参考值Vrefdc附近定义频带值。该频带等于

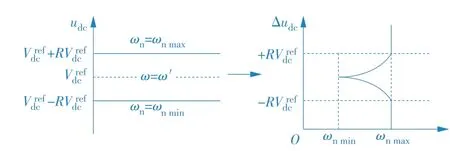
图5 ωn值的选择策略Fig.5 Selection strategy of ωn

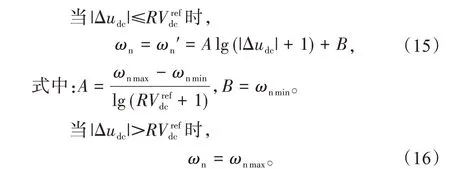
上述函数的主要目的为：当直流母线电压的误差值|Δudc|在瞬态期间增加，增加所选择的ωn；当所增加的|Δudc|超出参考电压波动范围时，则ωn值等于ωnmax。相反，在稳定状态下，电压误差值|Δudc|如果接近零，则所选择的ωn值必须近似等于ωnmin，以得到较低的电网电流THD。

通过对ωn值的选择，计算出不同情况下，电压外环PI 控制器中ki的值，从而达到最小化母线电压波动的目的。然而，在达到最小化母线电压瞬变的目的时，会对电网电流谐波产生影响，因此在最小化电压波动的情况下，还需对ζ进行选值，得出电压外环PI控制器中kp的值。最终通过得出的最优kp，ki来同时满足本文所需的2个目标。

2.2 自适应系统参数值的选取

由传统的双闭环控制环路的特征方程（如图3a所示）可知

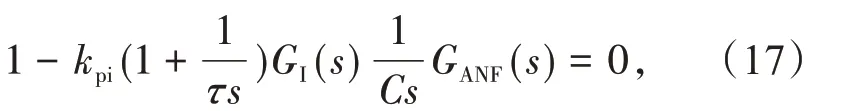
式中：τ为时间常数；GI(s)为电流环的传递函数；GANF(s)为滤波器的传递函数。根据文献［12］可知，该控制策略为总线电压控制回路实现了更高的带宽及更低的总线电压波动。控制环中τ的取值应越小越好。为此设置了当τ取不同值（τ=12.5，10.0，7.5，5.0 ms）的根轨迹，如图6 所示。由图可知，轨迹与实轴的交点随着τ从12.5 ms 减小到10.0 ms而向左移动，这意味着可能会减小总线电压的波动。但是，对于较小的τ（7.5 ms 和5.0 ms），根轨迹的形式会发生变化，并且根轨迹向不稳定区域发生变化。这意味着，使用常规方法，在保证根与实轴的交点的情况下，τ的最小值不能小于10.0 ms。因此，本文选择τ=10.0 ms作为设计增益。

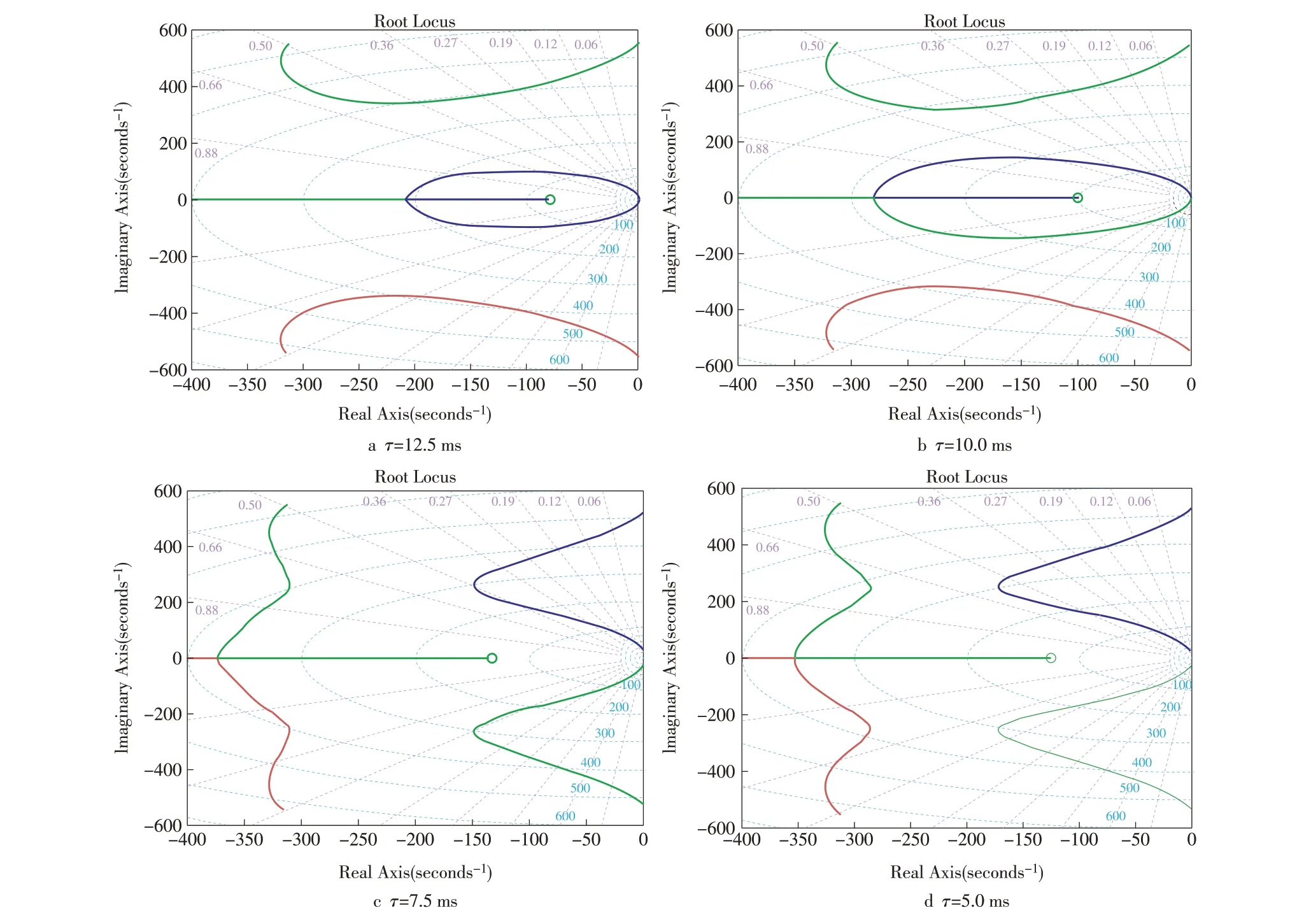
图6 常规控制方法中τ取不同值时的根轨迹（截图）Fig.6 Root loci of the traditional control method with τ taking different values（screenshot）

系统ζ的取值为0.5时，根据近似稳定时间公式

本文所提自适应控制方法中τ=12.5，10.0，7.5和5.0 ms 时的根轨迹如图7 所示。由图可知，与传统控制方法不同在于：当τ减小时不会改变轨迹的形式，因此可以选择较小的τ，并且可以设计波动较小的总线电压控制环路。通过以上分析，在本文提出的自适应控制方法中，选择τ=5.0 ms 作为设计增益。

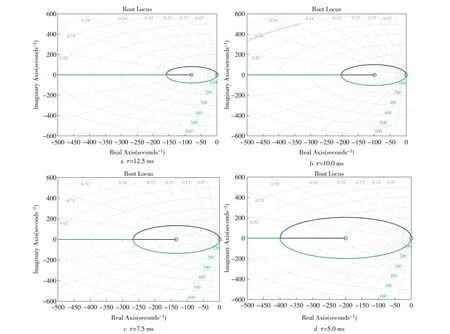
图7 自适应控制方法中τ取不同值时的根轨迹（截图）Fig.7 Root loci of the adaptive control method with τ taking different values（screenshot）

根据直流母线电压控制的τ为

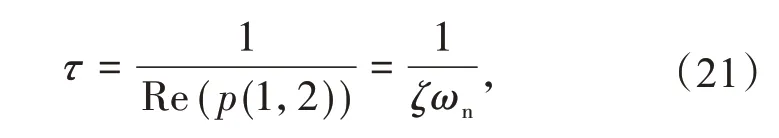
为寻求最优ζ的值，图8比较了当直流母线电容Cbus从1 mF 减小到75 μF，步长变化为25 μF 时，传统控制方法和所提方法的根轨迹。从图8a 可以看出，当Cbus减小时，传统方法的上下主磁极向虚轴（下阻尼）移动。在图8b中，所提方法的主极点的阻尼随着Cbus减小而增加。在本文中，Cbus=220 μF用于设计和实现所提方法和传统方法。可以看出，在Cbus=220 μF时，传统方法具有2对主极，每一极的阻尼约0.5；所提方法具有1对主极，阻尼约0.65，这使所提方法的总线电压波动较低。通过式（18）可知，传统方法ts≈63 ms，而所提方法ts≈21 ms。

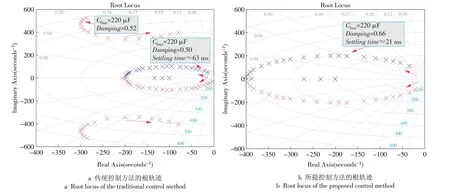
图8 当Cbus从1 mF减小到75 μF时控制方法的根轨迹（截图）Fig.8 Root loci of the control methods when Cbus decrease from 1 mF to 75 μF（screenshot）

因此本文选取阻尼比ζ=0.65，当τ=5.0 ms 时，根据式（22）可知

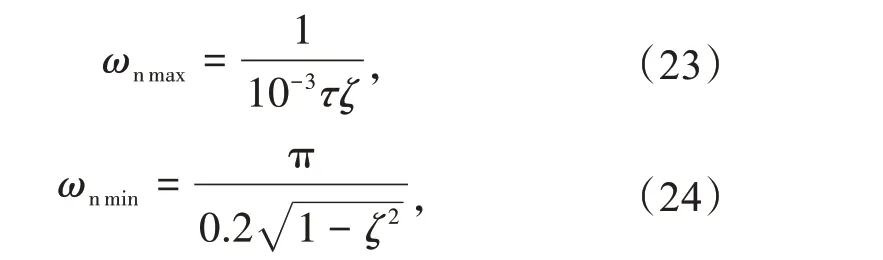
得出ωn的最大值和最小值分别为307，22。

经过所得数据进行仿真试验，结果符合本文所提控制策略，即在线调整ωn的值并根据ωn带来的交流侧电流的谐波畸变率的变化去调整ζ的值，该过程的目的在于最小化直流母线电压瞬变（瞬态期间）和电网电流THD 含量（稳态期间），使系统始终稳定在标准范围之内。

3 仿真与试验结果分析

为验证本文提出方法的可行性，在MATLAB/Simulink中建立图1所示的控制策略模型，并与传统的直流母线电压PI 控制器进行比较。模型参数见表1。

在微电网母线电压控制模型中，直流母线电容为220 μF，在1.0～2.5 s 时，微电网处于稳态运行模式；到达2.5 s 时，直流母线侧突增1 倍负载量，测试控制器的动态反应性能，试验时间为5 s。

3.1 试验1

采用传统的直流母线电压PI 控制方法，所得的试验结果如图9所示。

图9a 显示了当选取ωn=ωnmin，ζ=0.5 且在直流侧电压稳定后的2.5 s 时刻突增1 倍负载量时，所得的试验结果波形。其中图9a 上图显示直流母线侧峰值下冲电压为50 V，远超直流母线参考电压Vrefdc外部频带的容许极限。另一方面，对于电网电流，获得了可忽略不计的三次谐波分量，其仿真结果如图9a中图所示。通过用快速傅里叶变换（FFT）对电网电流分析可知，电网电流THD约为2.52%，突增1倍负载量后经过63 ms重新达到稳定。

图9b 显示了当ωn=ωnmax，ζ=0.5，同样也在直流侧电压稳定后的2.5 s 时刻突增1 倍负载量所得的试验结果波形。图9b 上图显示了直流母线侧峰值下冲电压为12 V，属于直流母线参考电压外部频带的容许极限范围之内。通过用FFT 对图9b 中图所示波形进行谐波分析，得到电网电流THD 约为13.3%，分析结果如图9b下图所示。

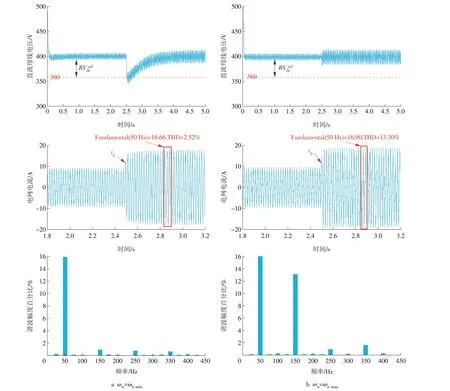
图9 传统PI控制策略波形（截图）Fig.9 Waveform of traditional PI control strategy（screenshot）

3.2 试验2

采用本文提出的一种改善并网整流器的直流母线电压控制性能的方法，即通过电压的差值在线调整ωn的值，且选取最佳阻尼比ζ=0.65时所得试验结果波形如图10所示。

由图10 上图可知，与传统控制方法相比，其系统动态响应更好，能在直流母线电压超过极限之前将电压值回升或降在电压波动的允许范围内，避免过大的电压降落对器件及系统带来的损坏。通过FFT 对电网电流的分析可知电网电流THD 约为2.78%，符合在降低电压波动水平的同时具有较低的电网电流谐波含量。且由图10 中图所示，经21 ms后系统重新达到稳定状态，恢复稳定时长小于图9a 上图中传统控制所需的63 ms。所以，通过对比试验表明本文所提方法相对于传统控制方法具有较小的系统误差、较短的稳定恢复时间。最终达到能最小化直流母线电压波动水平和较低的电网电流THD谐波的目的。

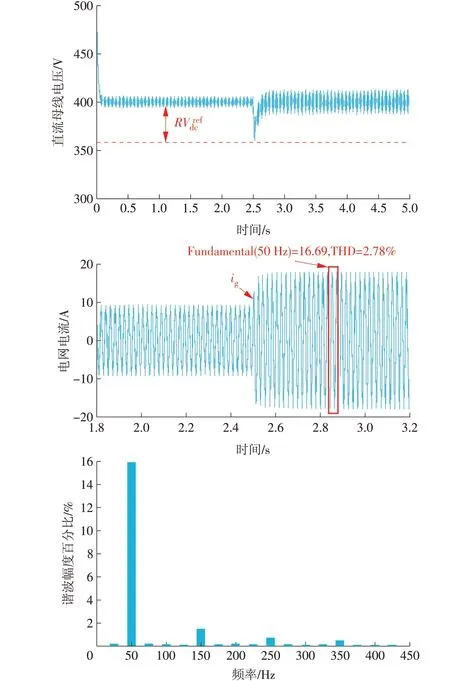
图10 自适应PI控制器的微电网直流母线电压控制策略波形（截图）Fig.10 Waveform of the DC bus voltage control strategy for microgrid based on adaptive PI controller（screenshot）

4 结论

本文提出了一种基于改进的自适应PI 控制器的直流微电网母线电压控制策略。相对于静态区域中的传统控制器，本文所提方法具有自适应PI 调节能力的电压外环控制回路，通过比例和积分增益的自调节，同时优化所有控制目标。在MATLAB/Simulink平台进行试验，得到如下结论。

（1）采用传统控制方法，当电压处于参考电压波动范围之内时，会存在较大的电网电流THD，值为13.30%；当电网电流THD 处于允许范围之内时（值为2.52%），会存在超出参考电压波动范围之外的电压值。

（2）采用本文所提控制方法，当电压处于参考电压波动范围之内时，电网电流THD 也处于允许范围之内（值为2.78%）。

（3）本文所设计的直流母线电压控制器具有以下特点：采用简化的PI 控制器确保直流母线电压的零稳态跟踪误差；在提升母线电压稳定性的同时，降低微电网注入电网电流的THD；实施难度小，具有一定的实用性。