考虑综合特征参数及主导动态相似性的大型工业企业负荷等值建模
朱红卫,王 毅,冷 军,赵慧勉,沈海中,李彦东
(伊犁新天煤化工有限责任公司,新疆 伊宁 835000)
0 引言
由于生产工艺的特殊性,冶金、煤化工等大型工业企业对供电的可靠性、安全性以及电能质量要求较高[1-2]。主电源故障导致电动机负荷失电时,将严重影响企业的安全生产运行,因此研究负荷母线失电残压[3]的变化规律,进而对快切装置[4]进行优化配置,对保证大型工业企业负荷的可靠供电具有重要意义。通常情况下,冶金、煤化工等大型工业企业负荷母线上带有多台不同容量的感应电动机负荷,且各类电动机参数也不尽相同,不同类型电动机对负荷母线的失电残压影响不同,因此对大型工业企业感应电动机负荷母线进行等值建模,掌握其整体动态,对于研究失电残压、保证可靠供电尤为必要。
早期在进行感应电动机等值建模时,常采用单机等值方法[5-9],在电动机型号或参数相差较大时误差较大。多机等值是目前常用的方法,而动态分群是多机等值的关键环节之一。文献[10]提出根据电动机惯量及暂态时间常数构建的特征指标进行分群,并进行了算例验证。文献[11]提出了表征电动机静态临界稳定特性指标,并依据该指标将电动机群分为稳定性好和稳定性差两类,据此进行动态等值。文献[12]提出了根据感应电动机的特殊运行条件进行动态等值的方法。上述基于特征指标或运行点的分群方法都无法体现感应电动机的整体动态,为此文献[13]提出基于感应电动机动态相似性的分群方法,动态相似性由感应电动机特征根的相似性距离表征;该分群方法的优点是能同时考虑感应电动机的稳态运行点及其动态特性,等值精度高;然而在分析电动机的动态特性时需计算所有特征根,计算量大。
为解决上述问题,本文提出基于感应电动机主导模态相似性的分群方法,只需计算电动机的主导动态,可极大减轻计算工作量,且具有较好的分群效果。
1 感应电动机的模型降阶
基于奇异摄动理论[14-15]进行感应电动机模型降阶。感应电动机采用以下3 阶实用极坐标模型:
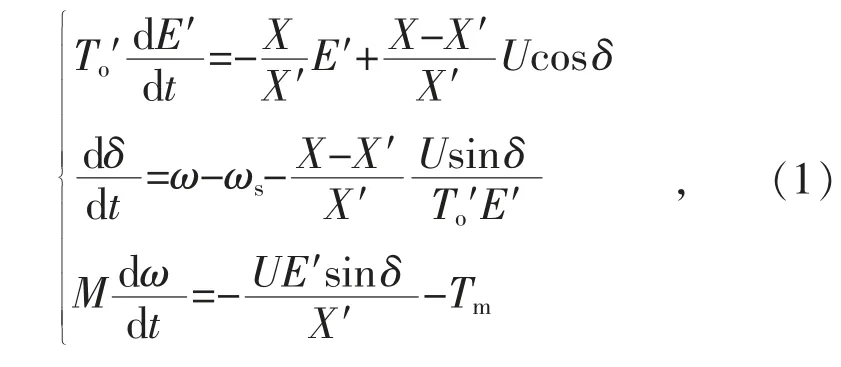
式中:E′和δ 分别为转子暂态电势和暂态电势角;ω 和ωs分别为转子角速度和系统同步角速度;为转子回路时间常数,=Xr/(ωsRr),其中Xr为转子电抗,Rr为转子电阻;U 为电动机端口电压;为暂态电抗,Xs和Xm分别为定子电抗和激磁电抗;M 为转子惯性时间常数;Tm=Tm0(aω2+bω+c)为电动机的机械负荷转矩,Tm0为稳态转矩,a,b 和c 为转矩系数;为考虑外部电抗时的时间常数。
根据式(1)的极坐标模型,文献[14]分别计算了一台额定容量为36 kW(小型)和一台额定容量为360 kW(大型)感应电动机的特征根及参与因子,结果表明:对于36 kW 感应电动机,其主导特征根参与因子最大的状态量为ω;对于360 kW感应电动机,其主导特征根参与因子最大的状态量为E′。因此,将动态由ω 主导的电动机称为小型电动机,由E′主导的电动机称为大型电动机。
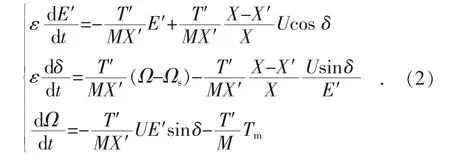
由于0<ε<1,因此式(2)为多时间尺度系统,其中快变量为E′和δ,慢变量为Ω。令:
根据奇异摄动理论,在研究感应电动机慢动态(主导动态)特性时,可将式(3)近似为E′≈,代入式(1)可得:
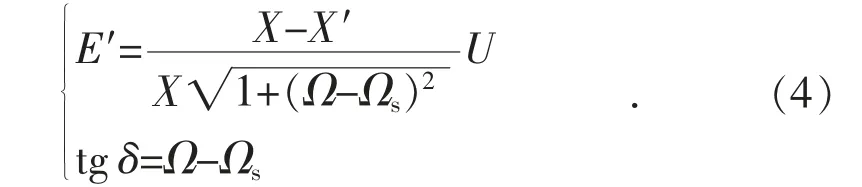
将式(4)代入式(3),可得慢变量Ω 的表达式:

根据奇异摄动理论,在研究感应电动机的慢动态(主导动态)特性时,可将式(7)近似为:
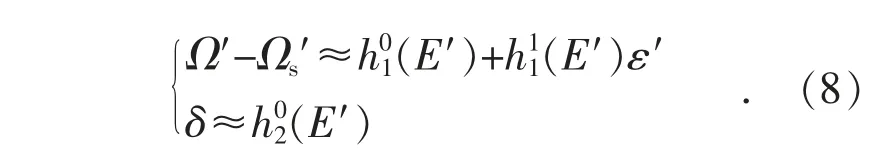
代入式(1)可得:
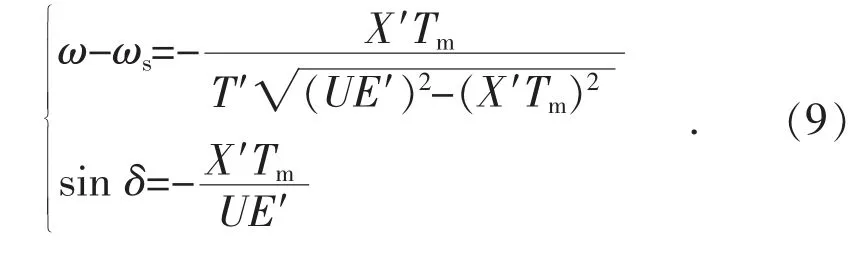
将式(9)代入式(7),可得慢变量E′的表达式为:
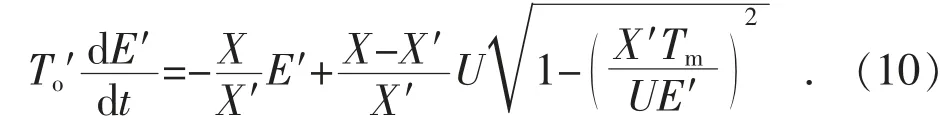
2 综合特征参数及主导动态相似度的感应电动机动态分群方法
2.1 感应电动机的主导动态
对于小型感应电动机,其主导动态可用式(5)表示。将其在运行点附近线性化,结果为:
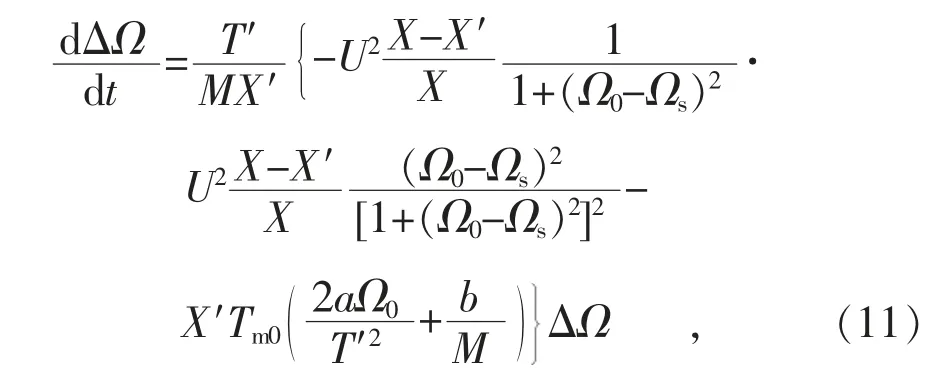
式中:ΔΩ 为Ω 的微小偏差量;Ω0为电动机稳态运行时的Ω 值。
计算式(11)的特征根:
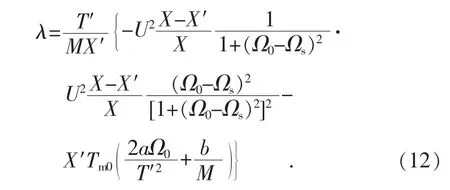
对于大型感应电动机,其主导动态可用式(10)表示。将其运行点附近线性化,可得:
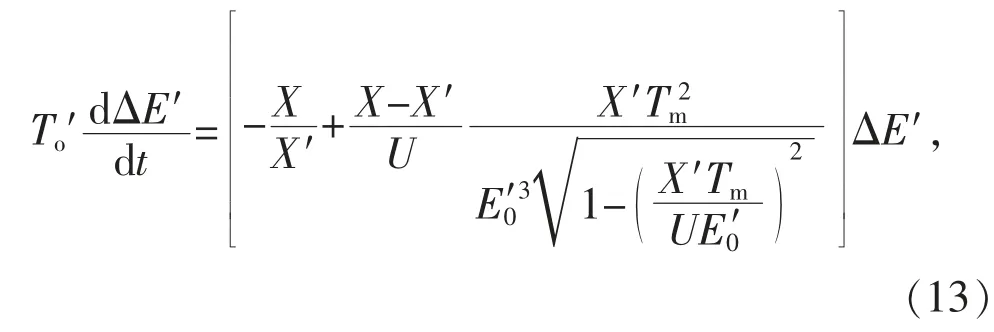
计算式(13)的特征根:
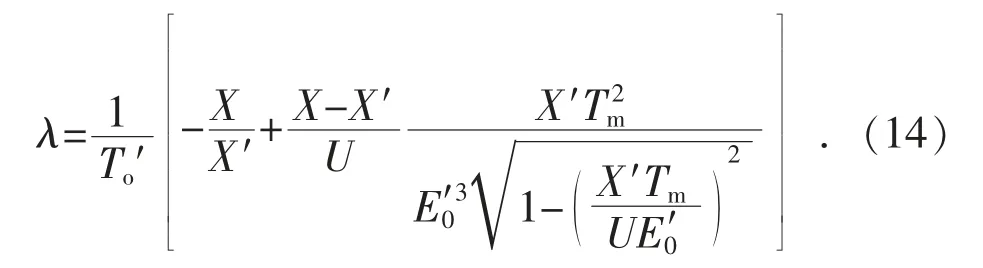
2.2 综合特征参数以及主导动态相似度的感应电动机动态分群方法
将电动机的动态相似性用特征根距离描述为:

式中:Dij为第i 台和第j 台电动机的动态相似性距离;λi为第i 台感应电动机的特征根。
Dij=0 时,2 台电动机的主导动态一致;Dij数值越大,2 台电动机的主导动态相差越大。因此在机组分群时:如果2 台感应电动机的相似性距离较小,将其分在同群;如果2 台感应电动机相似性距离较大,则分在不同的群。
分群具体流程见图1。
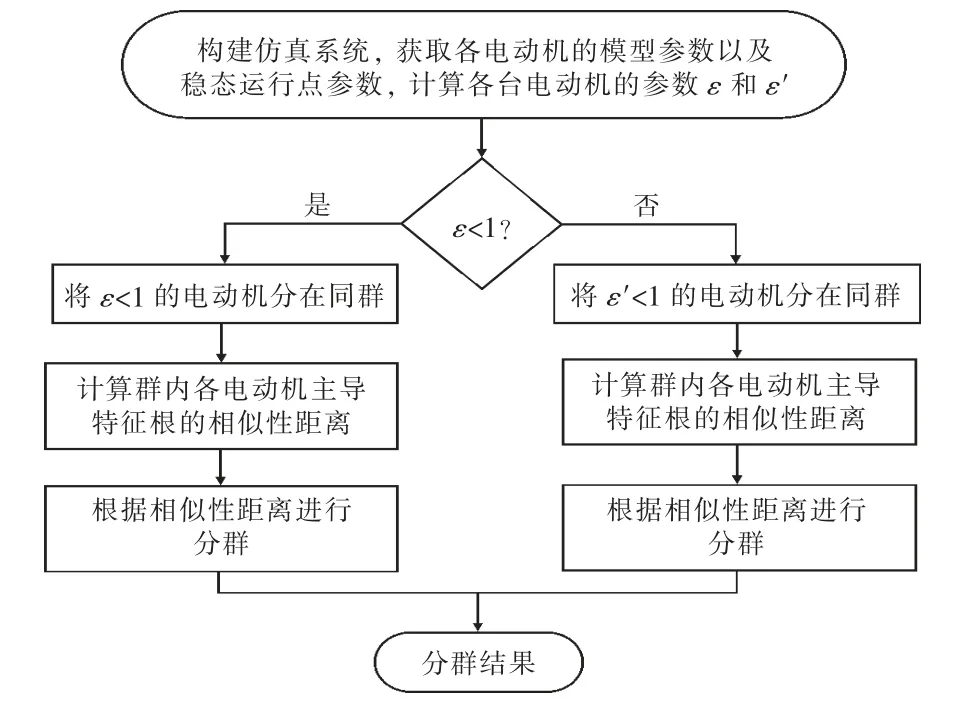
图1 感应电动机分群流程
2.3 等值电动机的参数聚合
根据上述方法的分群结果对电动机进行动态等值,等值电动机的参数采用按容量加权方法获得,具体为:
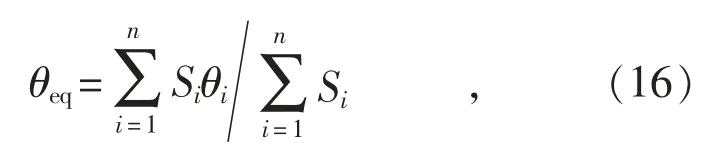
式中:θ 为感应电动机的参数,下标i 代表第i 台机组,下标eq 代表等值机组;n 为分在同群内感应电动机的数量;S 为感应电动机的额定容量。
3 算例分析
3.1 简单算例系统
以图2 所示的简单系统为例,8 台感应电动机(M1—M8)并接在同一母线上,通过Z=(0.8+j0.314)Ω 的阻抗与无穷大系统相连,其中Us为感应电动机负荷母线的电压,P 和Q 分别为8 台电动机总有功功率和无功功率。
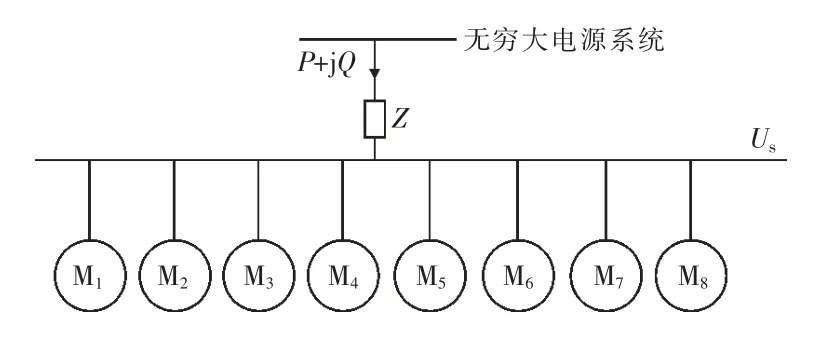
图2 含8 台感应电动机的无穷大系统
计算各台电动机的特征参数ε 和ε′,结果见表1。
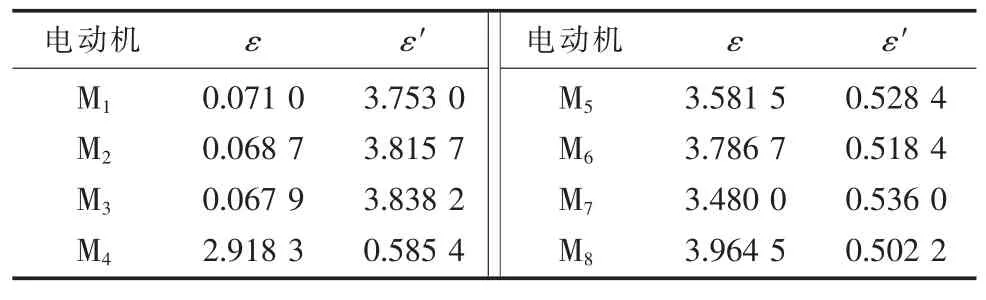
表1 感应电动机的参数ε 和ε′
从表1 可以看出:电动机M1—M3的参数ε满足0<ε<1,为小型电动机;M4—M8的参数ε′满足0<ε′<1,因此为大型电动机。
根据式(12)和(14)分别计算各台电动机的主导特征根,结果见表2。

表2 各感应电动机的主导特征根
根据式(15)计算得到的主导特征根相似性距离(图3),对电动机进行分群;采用文献[10]提出的方法,根据参数的数值进行分群;基于感应电动机全部特征根的相似性距离进行分群。上述3 种方法的分群结果见表3。
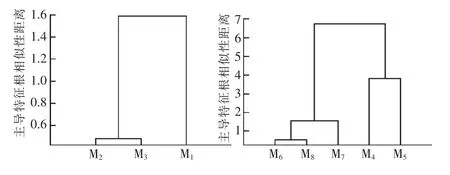
图3 主导特征根相似性计算结果
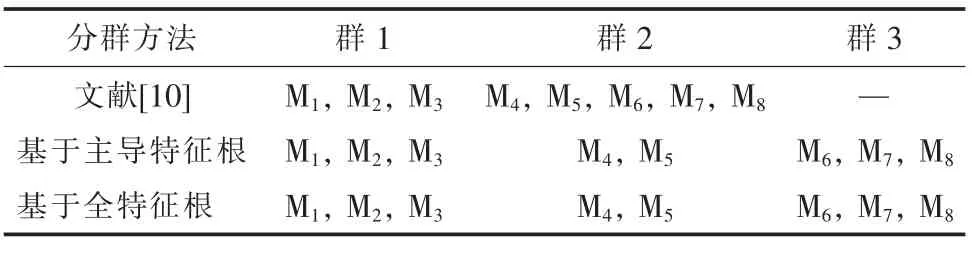
表3 算例1 的分群结果
从表3 可以看出,本文所提出的基于主导特征根的分群结果与基于全特征根相似性的分群结果一致。因此,将图1 中的8 台电动机等值为3台等值机,各等值机的参数按式(16)计算。
为验证上述分群方法的可行性,进行扰动仿真分析。扰动设置为负荷母线在0.1 s 时发生三相短路故障,故障持续0.1 s 后切除,仿真时长为0.8 s。3 种分群方法下的等值机与原系统的仿真结果对比见图4。

图4 等值前后感应电动机的受扰轨迹
从图4 可以看出:文献[10]的分群结果有一定的误差;根据主导模态分群和根据全模态分群均有较好的等值结果。
3.2 某大型煤化工企业10 kV 母线感应电动机的动态等值
为了验证本文所提方法对于实际系统的应用效果,以某大型煤化工企业10 kV 净化系统为例进行仿真。该系统母线接有5 种类型的感应电动机,接线方式同图2。
3 种方法的分群结果见表4,可以看出基于主导特征根相似性的分群结果与基于全部特征根相似性的分群结果一致。
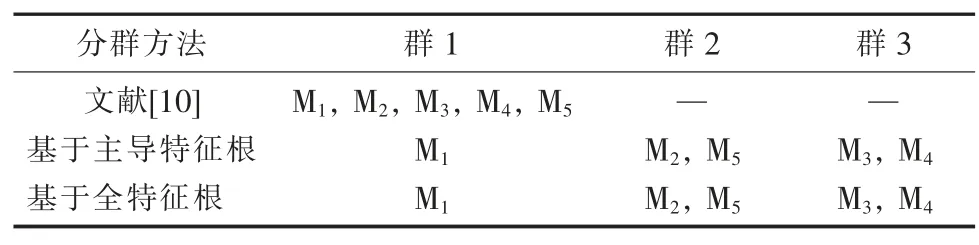
表4 某煤化工企业10 kV 母线的感应电动机分群结果
根据表4 的分群结果,采用按容量加权方法计算等值电动机的模型参数。为验证等值结果的可行性,扰动设置为电动机负荷母线在0.1 s 时发生三相短路故障,故障持续0.1 s 后切除,仿真时间为3 s。3 种分群方法下的等值机与原系统的仿真结果对比见图5。
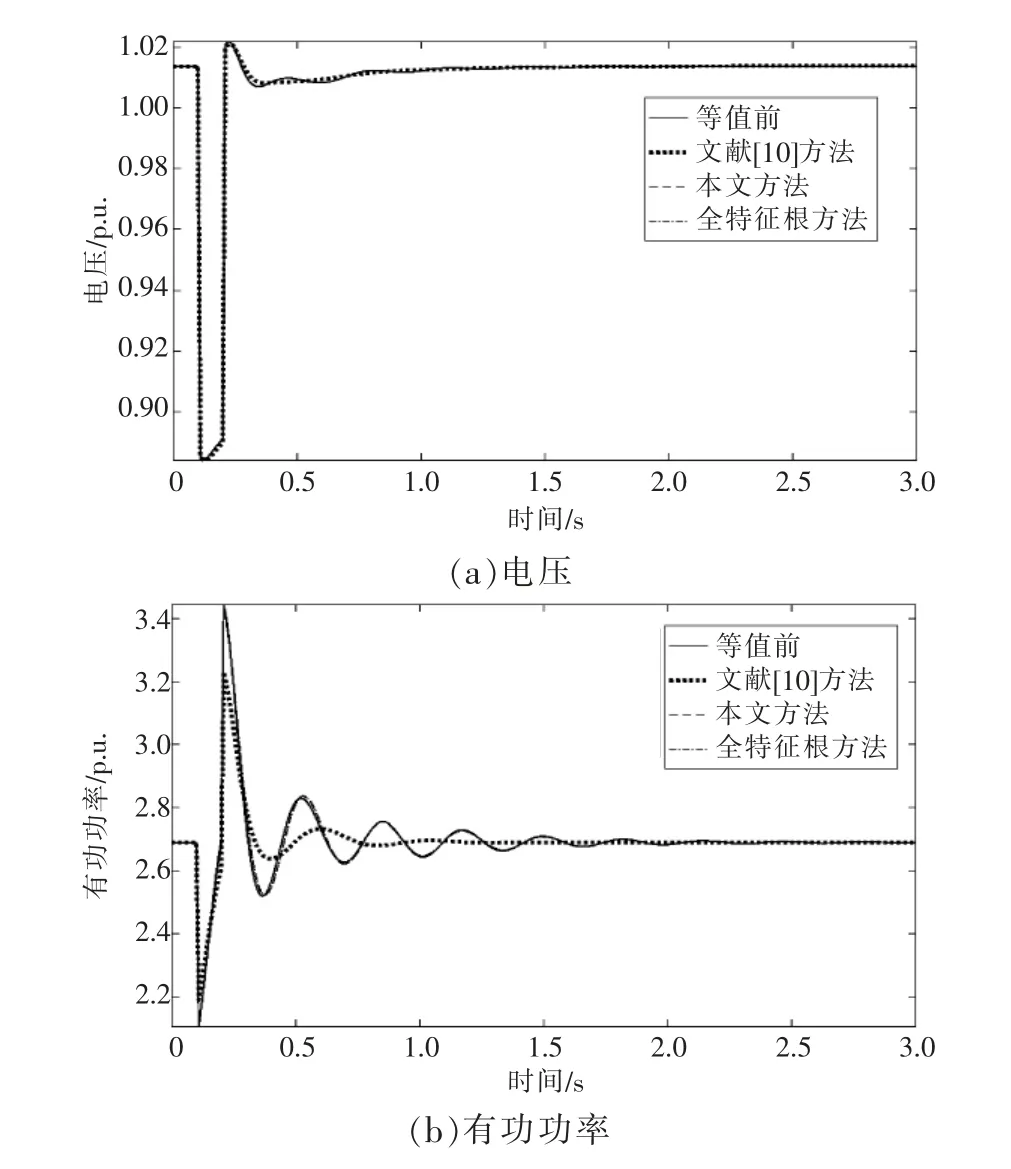
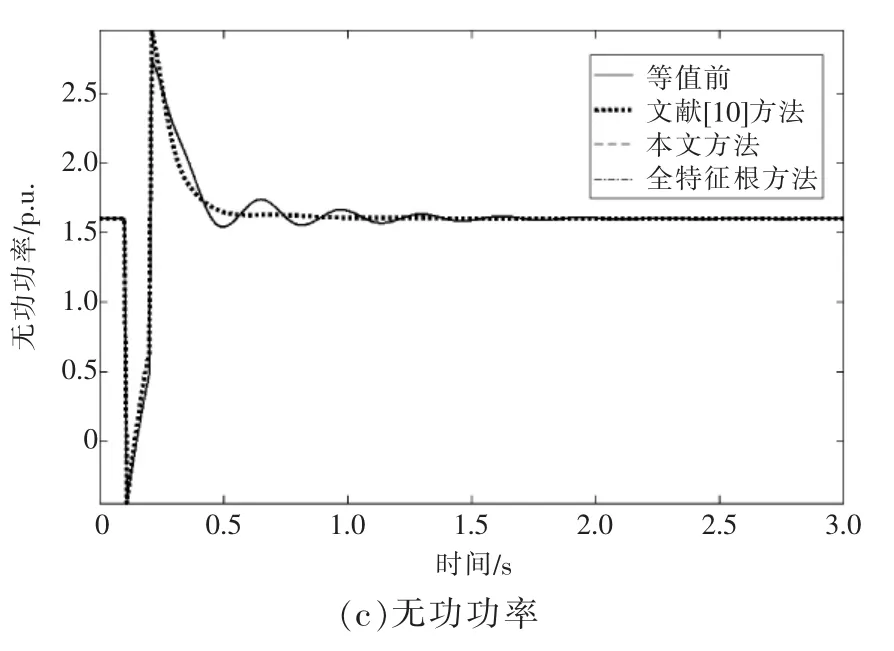
图5 等值前后受扰轨迹
从图5 可以得出与图4 算例系统相同的结论:如果仅根据电动机的大小来进行分群,结果有一定误差;根据特征参数及主导模态分群,以及根据全模态分群,均有较好的等值结果。
4 结语
基于特征参数以及主导动态相似度进行感应电动机动态等值时,首先根据特征参数对电动机进行分群,然后将同群内的机组根据主导动态相似性进一步分群。与现有特征参数方法相比,本方法的精度较高;与全特征根相似性方法相比,本方法计算量小,同时还具有较高的精度。
下一步将继续研究非主导特征根对分群以及等值精度的影响、现有各分群方法的适应性,以提高本文方法的有效性。

