基于多路径广度优先搜索算法的代谢通路设计与实现

黄祖成 沈梦圆 侯至丞* TOKUYASU Taku Andrew 蒙海林*

1(广州中国科学院先进技术研究所 机器人与智能装备研究中心 广州 511458)

2(广州中国科学院先进技术研究所 生物工程研究中心 广州 511458)

3(中国科学院深圳先进技术研究院 深圳合成生物学创新研究院 中国科学院定量工程生物学重点实验室广东省合成基因组学重点实验室 深圳 518055)

1 引 言

代谢通路(Metabolic Pathways)是指生物体内将源代谢物转化为目标代谢物的一系列连续的酶催化反应[1]，如糖酵解通路、三羧酸循环、梭状芽胞杆菌固定二氧化碳的 Wood-Ljungdahl 通路[2]、蓝藻吸收氨的谷氨酰胺合成酶循环(GSGOGAT)[3]等。在合成生物学领域，常常需要对代谢通路进行设计与分析。代谢通路设计的目标是给定一个或者若干个起始和目标化合物，从代谢数据中找到并返回生物相关的、由酶催化反应构成的、有特定功能和作用的、从起始化合物到目标化合物的可行路径[4]。在过去的十多年里，随着实验技术的进步，高通量组学数据日益增长，越来越多的代谢通路得以解析。以 KEGG[5]和 MetaCyc[6]为代表的代谢数据库发展迅速，为识别和发现新的合成替代路径带来了新的机遇和挑战。研究人员根据不同物种的代谢数据特点和生物合成的实际应用需求，开发了多个代谢通路设计算法和工具，如 MAPPS[7]、路径搜索系统[8]、novoPathFinder[9]、MRSD[4]、FogLight[10]和 Metabolic Tinker[11]等。这些软件从算法选择上可以归为基于图论[12]、基于化学计量学[13]和基于逆合成[14]等不同类别。利用这些工具，研究人员可方便地从代谢数据中识别、设计出具有潜在价值的代谢通路[15]。

搜索算法是代谢通路设计工具的核心步骤。在代谢网络较大时，现有的代谢设计工具存在搜索时间相对较长的问题。为此，现有的代谢设计工具尝试从数据结构上对算法进行优化[16-17]，或在路径选取策略上进行优化[18]。此外，在多路径搜索算法方面，传统的前K条最短路径算法(K-Shortest Path，KSP)是以 Yen’s 算法为代表。该算法是基于 Dijkstra 算法进行演化的版本，在搜索功能上实现了较为有效的前K条最短路径搜索，但其算法过程从第 3 条路径开始则需要提升。另外，综合来看 KSP 算法的核心思想都是边删除选择法，而过去众多算法围绕数据结构及路径选取策略上进行过优化，也取得了一定的性能提升效果。近年来，由于计算机硬件性能的提升，传统 KSP 算法优势变得不再明显。因此，本文基于 Yen’s 算法进行优化改进的 KSP 算法，在对路径选取策略进行优化的同时，结合多核心CPU 计算机硬件特点，使用并行计算方式来进一步提升代谢通路搜索算法的运算性能。

2 数据建模

本文主要是针对合成生物学的代谢网络路径搜索进行优化，代谢网络数据来源于 KEGG 通路数据库(https://www.kegg.jp/kegg/pathway.html)。通过 KEGG API 接口批量下载不同物种及参考的代谢反应图的 KGML 文件，并进行解析来提取化合物和反应方向。将代谢通路表示为图，图中的节点表示为代谢通路中的化合物(代谢物)，边表示化合物之间的转化(化学反应或代谢反应)。本文设计的代谢网络路径搜索模型针对 KEGG数据格式的特点进行了专门优化。在不考虑能耗和确保路径正确的前提下，针对可能存在的代谢通路，尽可能搜索多条路径，把代谢网络数据简化以提高搜索的效率。具体处理方法为：把具有通路的化合物之间的 Cost 值设为 1，不连通的化合物之间的 Cost 值设为 max(实验时，考虑到KEGG 代谢网络参考图中化合物数量约为 3 000个，设 max＝9999)。所生成的代谢网络图的邻接表如下：

3 算法设计

3.1 传统 KSP 算法

传统 KSP 算法主要以 Yen’s 算法为代表。其中，Yen’s 算法是 Yen 在 1971 年提出并以其名字命名的算法。Yen’s 算法采用了递推法中的偏离路径算法思想，适用于非负权边的有向无环图结构。其主算法步骤如下：

(1)在非负权边的有向无环图G中，使用Dijkstra 算法找出第一条从起点S到终点D的最短路径P1，加入集合 A(已选路径集合)；

(2)从集合 A 中选择最后加入的一条路径Pn，在G中依次删除路径Pn中的边(把边的 Cost值设为最大)，并使用 Dijkstra 算法计算出对应的最短路径PNi加入集合 B(候选路径集合)；

(3)从集合 B 中选出一条 Cost 最小的路径Pm，加入集合 A 并从集合 B 中删除Pm；

(4)重复步骤(2)～(3)直到集合 A 的数量达到K，则集合 A 为所求的前K条最短路径。

本文将步骤(2)～(3)定义为次短路径搜索(Second Shortest Path Search，SSPS)过程。在KSP 算法中，最耗时的运算是 Dijkstra 运算，而该算法中的 SSPS 过程存在较多重复的 Dijkstra计算。因此，在节点数量较多的网络中进行 KSP运算将会耗费较长时间。本文主要研究如何对SSPS 过程进行优化以减少不必要的 Dijkstra 运算，从而提高 KSP 算法性能。

3.2 加速选择法

在 Dijkstra 路径搜索算法中，一次只能找出一条最短路径，但 Cost 相同的最短路径可能并不唯一。在 SSPS 过程前，集合 B 中可能已经存在所需要的最短路径。在合成生物代谢网络中，所有连通的边的 Cost 值设为 1，此时 Cost 值相同的路径都认可为是最短路径，但并不设先后顺序。因此，若在集合 B 中存在与集合 A 最后一条路径 Cost 值相同的路径，则可认为是在集合 A之后的最短路径。此时，可直接从集合 B 中选择出最短路径Pn，则省去了 SSPS 的计算过程。

如图 1 所示，当前需要搜索第 4 条最短路径时集合 A 中已有 3 条路径，集合 B 中 Cost 值最小的路径与集合 A 的最后一条路径 Cost 值相等，此时直接从集合 B 中选取 Cost 值为 5 的路径加入集合 A 中作为第 4 条最短路径，从而节省了一轮 SSPS 运算(此例子中可节省 4 次 Dijkstra运算)。

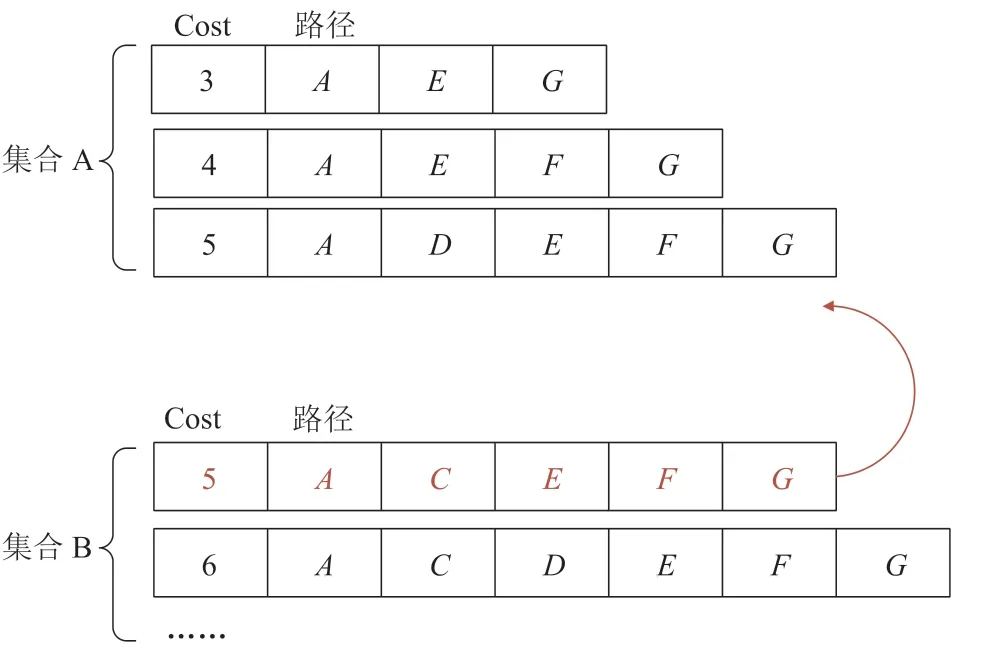
图1 加速选择法Fig.1 Accelerated selection method

3.3 删除重复候选路径

在一个 SSPS 过程中，得出的候选路径可能与上一轮 SSPS 得到的候选路径存在相同的，此时需要判断，当路径已存在集合 B 中则不加入到集合 B。如图 2 所示，删除边BC或CD所产生的候选路径是相同的，此时只选择一条加入集合B 即可。

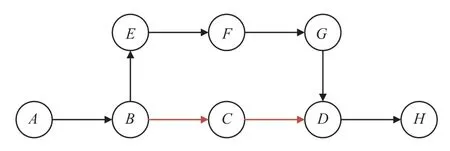
图2 相同的候选路径Fig.2 The same candidate pathways

3.4 记录已选边

在已找到的路径集合 A 中，除第一条路径外，其他路径都有对应删除的边，这些边的集合记为 EA。在进行 SSPS 过程前，先在图G中删除 EA 里的边，可减少重复的 Dijkstra 运算。

如图 3 所示，集合 A 中第二条最短路径所对应的边为BD，在进行下一轮 SSPS 运算前把边BD删除以减少 SSPS 的运算时间(此例子中减少了 1 次 Dijkstra 运算)。

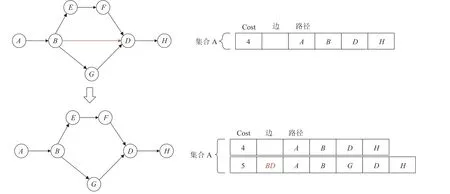
图3 记录已选边Fig.3 Recording the selected edges

3.5 记录关键边

关键边(Critical Edge)是从起点到终点的必经之路，在一个 SSPS 过程中跳过关键边的 Dijkstra运算可节省运算时间。具体做法为：在 SSPS 过程中，若 Dijkstra 运算的结果 Cost 是最大值，则把对应的边加入到关键边的集合 C 中；随后在下一轮 SSPS 过程中跳过关键边的 Dijkstra 运算，可节省运算时间。

如图 4 所示，当经过一轮 SSPS 运算后，可以得到边AB和DH为关键边，并在下一轮 SSPS运算时把关键边排除，以减少运算量(此例子中节省 2 次 Dijkstra 运算)。

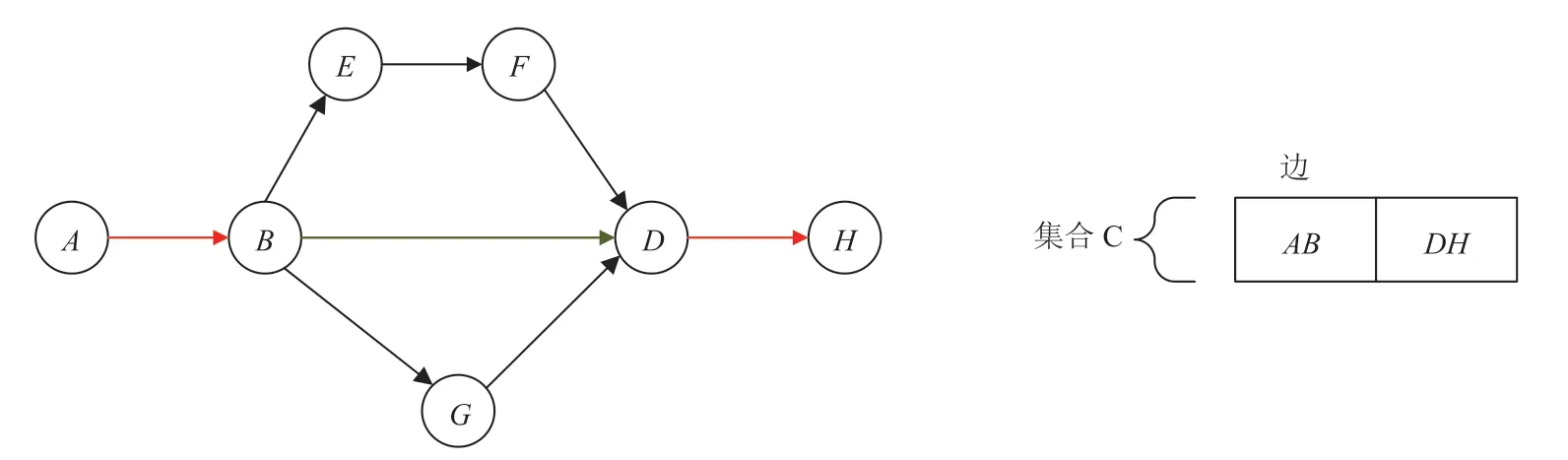
图4 记录关键边Fig.4 Recording the key edges

4 平台实现

平台采用 Flask＋Vue 框架，实现前后端分离。核心算法代码采用 C++实现以提升运算速率。代谢网络数据主要来源于 KEGG 数据库，在路径搜索前把 KEGG 数据进行初始化(KEGG 数据库转化为邻接表)以便进行 KSP 算法运算。系统主要程序流程如图 5 所示。KEGG 数据的初始化在系统启动前期执行，此部分程序运行时间约为 3～5 s，这对用户来说并不产生影响。对系统用户产生影响的过程为 KSP 运算部分，这也是本文主要的研究工作。

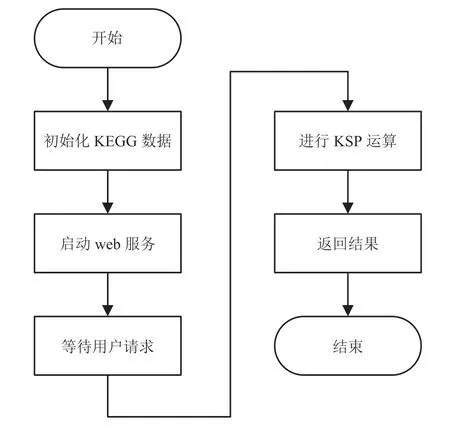
图5 程序主流程Fig.5 The flow chart of the program

图6 所示为改进的 KSP 算法流程，其中SSPS 过程采用了并行方式同时进行多个 Dijkstra运算，算法时间复杂度从O(n×m)减少到O(n)，算法结束后会产生K条最短路径。为提高用户体验，在实际应用系统中每产生一条最短路径则返回到用户界面上显示，这样可以减少用户主观的等待时间。图 7 所示用户系统界面，搜索得到的路径为按短到长依次显示。

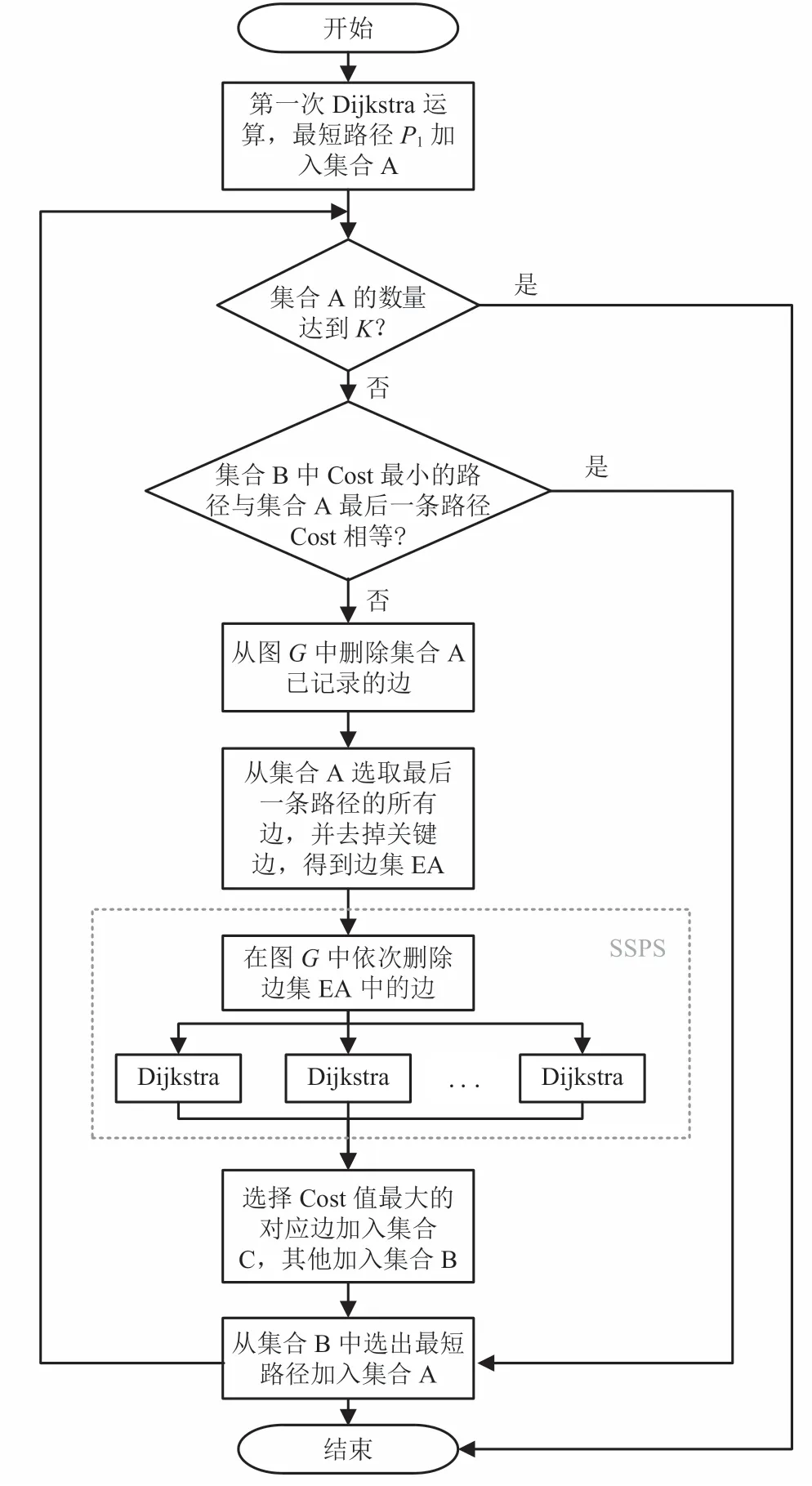
图6 改进的 KSP 算法流程Fig.6 The flow chart of improved KSP algorithm

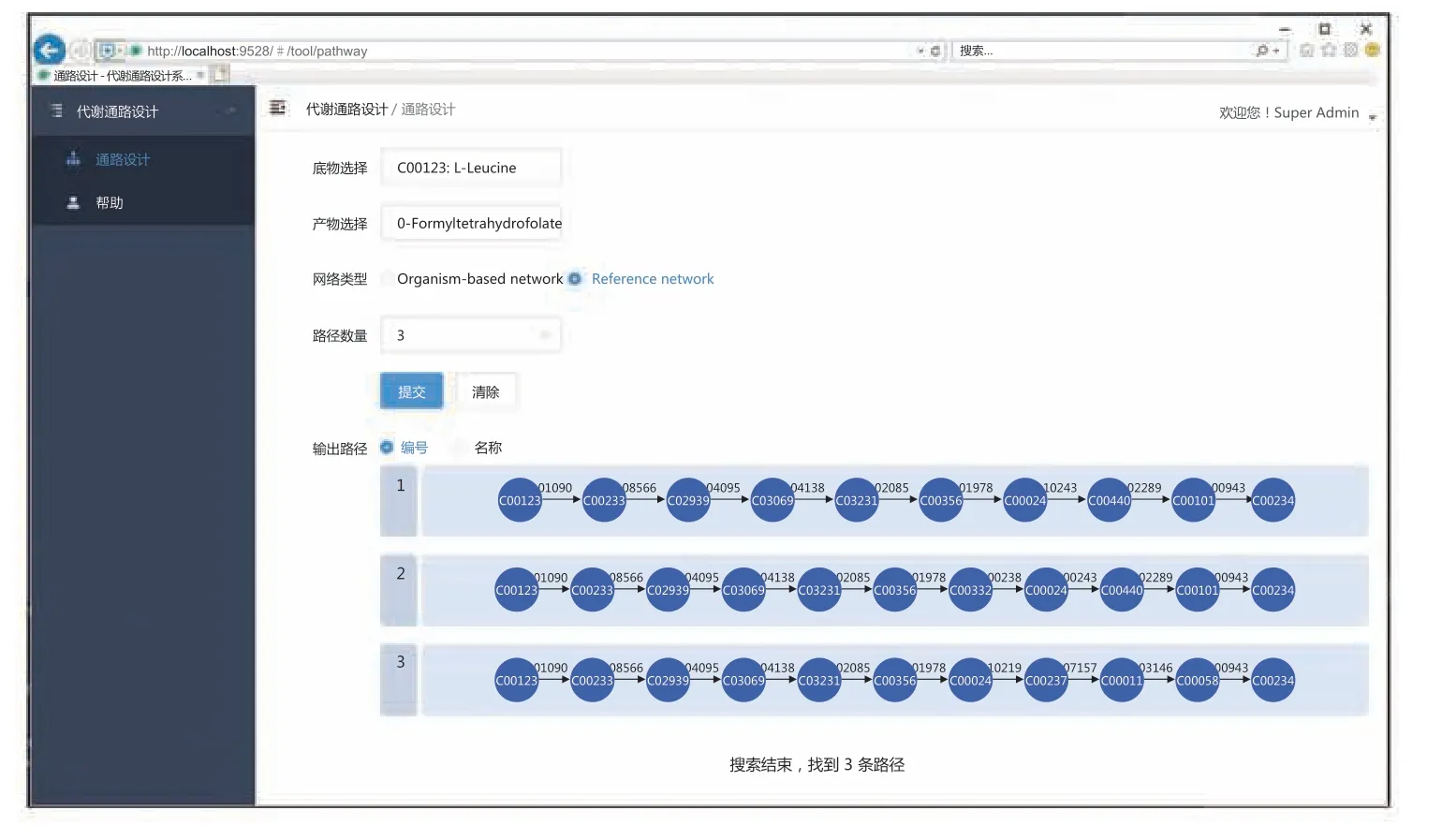
图7 系统界面Fig.7 The system interface

5 算法性能测试

在实验数据中，随机选取起点和终点，分别设定最短路径数量为 1～7 条，观察算法所调用 Dijkstra 的次数来分析算法的性能。具体数据如表 1 所示。

从表 1 可知，当路径数量K大于 2 时，改进的 KSP 算法在性能上有 2～3 倍的提升，并行的KSP 算法在性能上有 5～9 倍的提升，并随着路径数量的增加而不断提升。本次改进的 KSP 算法性能提升较为显著。

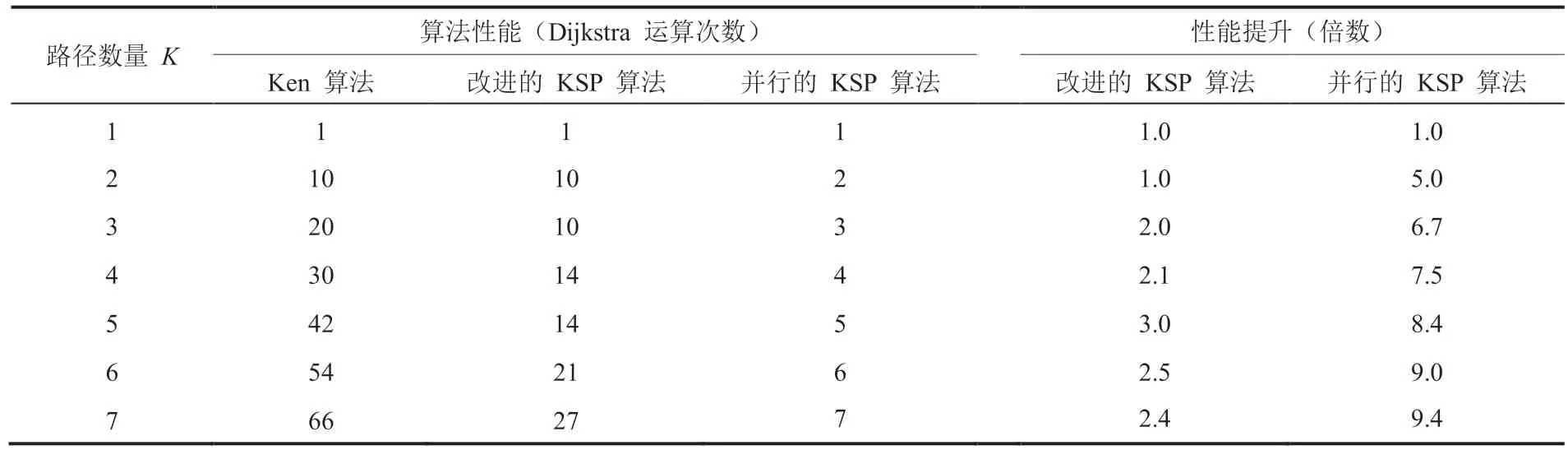
表1 改进的 KSP 算法性能对比Table 1 The performance of improved KSP algorithm

表2 数据为随机选取 4 条目标路径进行前 7条最短路径的搜索，每条路径的平均搜索时间为0.27～0.39 s。其中，所选取的 KEGG 参考代谢网络图节点总数为 2 828，边总数为 4 051。即使在 KSP 算法运算时间上增加 0.5 s 的 http 请求及获取化合物及反应信息所需要的时间，在用户端平均每条路径的搜索总时间仍然小于 1 s，提升了系统的用户体验。

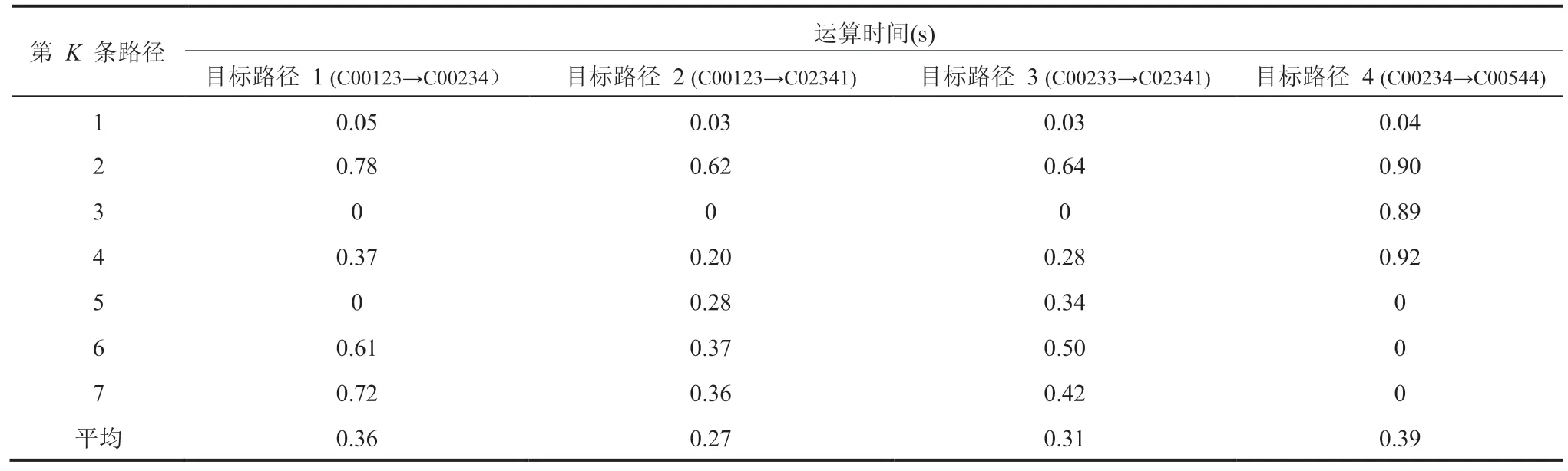
表2 改进的 KSP 算法性能实测数据Table 2 The performance data of improved KSP algorithm

6 讨论与分析

在合成生物学设计尤其是细胞工厂/底盘细胞设计中，代谢通路设计工具可有效辅助研究人员快速找到出发底物及目标产物之间的连接路径，提高设计效率。例如，Yim 等[19]对 1,4-丁二醇(Butane-1,4-diol，BDO)的合成代谢通路进行 1万多次的计算调查后，设计获得最佳途径，并在大肠杆菌中获得高达 18 g/L 的 BDO。随着下游酶的改善，BDO 滴度提高到 110 g/L。该案例成功展示了代谢通路设计算法在生物合成中的巨大应用潜力。

本文主要针对基于图论的路径搜索算法进行性能优化，用于代谢通路的搜索和发掘。该类算法通过代谢网络中的化合物和化学反应之间的连接关系来搜索可行的代谢通路。目前，该类算法的代表软件主要有 MRSD[4]、FogLight[10]和Metabolic Tinker[11]等。其主要优点是可以在单一物种或者跨物种中寻找可行的代谢通路，不受物种和反应流平衡等约束；缺点是在找到的代谢通路中容易出现一些连通度高的簇代谢物，而这些簇代谢物的存在会影响整体路径的生物化学意义[11]。

在图论中，路径搜索算法主要有 Dijkstra 算法、A*算法、Bellman-Ford 算法、Floyd-Warshall算法和 Johnson 算法等。其中，A*算法在有估价函数的条件下可以快速搜索目标路径；Bellman-Ford 算法可以处理含负边值的路径；Floyd-Warshall 算法实现代码简单；Johnson 算法在 Bellman-Ford 算法的基础上优化并提高了稀疏图的运算效率；结合生物学代谢网络中为搜索单源非负边的路径，Dijkstra 算法在时间复杂度上更有优势。自 Dijkstra 算法提出以来，许多学者都对它进行过不同程度的优化以提高其性能。在后来的多路径搜索(KSP)算法上，大部分研究围绕删除路径核心思想进行了许多的改进[16-18]。这些改进的算法在过去计算机性能有限的条件下取得了较好的效果，算法时间复杂度从O(n×n)→O(n×m)→O(n×logm)不断提升。但随着计算机性能的提升，特别是多核心 CPU 以及多CPU 架构的计算机系统的广泛应用，传统以单线程进行算法迭代运算的方式并不能发挥很好的效果。本文正是利用了多核心 CPU 的硬件特点，在算法优化的同时采用并行编程方式，把算法的时间复杂度提升到O(n)水平，大幅提升了运算性能。

7 结论

本文针对合成生物学代谢网络中代谢通路非唯一以及传统 KSP 算法效率偏低的问题，对 KSP算法进行改进优化以提升运算性能。在对 KSP 算法策略上优化的同时，采用并行计算方式进一步提升算法的性能。使用 Python 实现代谢通路设计Web 平台，并采用 C++编写核心算法的代码。通过引入 KEGG 代谢网络图，验证改进的 KSP 算法比传统 KSP 算法有较大的性能提升，在合成生物学代谢通路设计上具有一定的应用价值。然而，由于代谢反应在不同物种的代谢网络中会有差别，本文基于 KEGG 参考图上进行了搜索算法的研究，并未对物种的特性进行区分。因此，后续工作可在 KEGG 参考图基础上针对不同物种的约束条件进行路径算法研究，以适应合成生物学对不同物种代谢网络通路设计的特定需求。