基于证据预处理的协作频谱感知方法

任欣悦， 孙志国， 陈增茂， 刁鸣

(哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨 150001)

认知无线电技术[1]可有效解决频谱资源利用率低的问题。频谱感知技术[2]可以感知频段的占用情况，为认知无线电技术提供先验信息。协作频谱感知技术[3-4]可以综合考虑多个感知用户的检测结果，它可以减小干扰、衰落等对检测结果的影响，增加检测结果的可靠性。数据融合方法是协作频谱感知的核心，但传统融合方法[5]均未考虑复杂信道环境变化会使感知结果具有不确定性。

针对融合信息的不确定性问题，文献[6-7]提出基于DS证据理论的融合方法。但由于无线环境的复杂性(干扰、衰落和恶意用户等)，会使感知结果产生冲突数据，加上DS合成公式归一化的弊端，会出现合成公式不能使用或合成结果与理论相悖的问题，即证据悖论问题。目前，解决方法分为改进合成公式[8-13]和修正证据源[14-18]这2个方向。前者实质是解决冲突的分配，该方法收敛性好，但并未从实际减少信息的不确定度。如文献[8]将冲突值分配给不确定项，该方法适用于处理低冲突，对于高冲突完全失效。文献[10]引入可信度和平均支持度来分配冲突，但却增大了证据的不确定性。后者实质是对证据预处理增加可靠性再融合，该方法修改了原始非冲突数据，应用时存在风险。如文献[16]利用距离测度计算出可信度作为权重，修改了原始非冲突数据，并且融合时用加权平均的方式代替合成规则，收敛性差。

本文针对证据悖论问题，结合以上2大类方法的优缺点，提出一种基于证据预处理的协作频谱感知方法，仅对冲突数据进行修正，用来降低修改非冲突数据的风险，并提出一种新的合成公式对预处理后的证据值进行融合，通过仿真分析验证了该算法的鲁棒性和检测性能。该算法的优点是修正冲突数据，保留原始非冲突数据，可靠性高，鲁棒性强。

1 协作频谱感知系统模型

协作频谱感知系统模型如图1所示。该系统分为2个过程实现。首先，n个感知用户对主用户进行频谱感知；其次将感知结果发送到融合中心进行融合和判决。

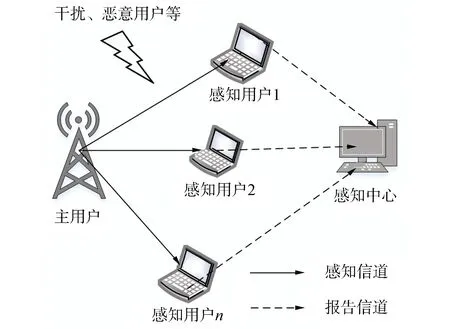
图1 协作频谱感知系统模型Fig.1 Cooperative spectrum sensing system model

1.1 本地频谱感知模型

利用二元假设检验模型，对本地频谱感知建模。H1代表主用户存在，H0代表主用户不存在，即：

(1)

式中：i=1,2,…,n，n是感知用户数；s(k)表示主用户的发送信号；yi(k)和ni(k)分别表示第i个感知用户接收的信号和噪声，hi表示信道增益。

频谱感知方法采用能量检测法[19]，得到的本地检测量为：

(2)

式中N=2TW是采样个数，T为检测时间，W为信号带宽的乘积。当N足够大时，式(2)可近似为高斯分布：

(3)

式中：均值分别为μ0i=N和μ1i=N(1+γi)；方差分别为σ0i=2N和σ1i=2N(1+2γi)；γi是信噪比。

1.2 基于DS证据理论的融合模型

在协作频谱感知系统中，DS证据理论的识别框架可定义为Θ={H0,H1,Ω}，Ω代表信息的不确定性。根据式(3)，利用高斯函数构建第i个感知用户的基本概率分配(basic probability assignment， BPA)函数为：

(4)

(5)

mi(Ω)=1-mi(H1)-mi(H0)

(6)

利用传统的DS合成公式融合所有感知用户的BPA值。

(7)

(8)

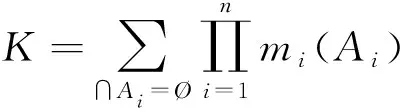
根据式(7)和式(8)得出的结果进行判决:

(9)

2 协作频谱感知算法设计

本文在第1节中所述的系统模型基础上，提出一种改进方法，可有效处理证据悖论问题。该方法分为2个过程进行，分别为证据预处理和证据融合。

2.1 证据预处理

证据预处理的基本思想是利用感知用户的可靠性对感知用户的BPA值进行修正。本文用静态权重和动态权重来衡量感知用户的可靠性。

2.1.1 确定静态权重

静态权重主要体现在感知用户自身的可靠性。因此，利用感知用户的信噪比这一先验信息设置静态权重：

(10)

利用静态权重对所有感知用户的BPA值进行修正：

(11)

(12)

(13)

2.1.2 确定动态权重

动态权重主要体现在感知用户之间的相互支持度, 可间接体现感知用户的可靠性。

首先计算任意2个感知用户间的相似系数：

(14)

式中Ak⊆Θ，i=1,2,…,n，j=1,2,…,n。

(15)

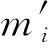
(16)

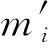
(17)

式(17)称为感知用户的动态权重。

2.1.3 冲突证据的确定及修正

假设有n组证据，以平均权重为阈值，利用动态权重来确定冲突数据:

(18)

冲突数据确定后，仅对冲突数据进行修正，既修正冲突数据,又保证原始数据自身的可靠性。

结合静态权重和动态权重，设置修正系数为：

βi=λwi+(1-λ)crd_nori

(19)

式中：λ为比重值, 0≤λ≤1 。可通过调节λ值来改变感知用户的2种权重对修正系数的比例影响。

利用式(19)对冲突数据进行修正：

(20)

修正后的冲突数据对假设H1和H0支持度减少，对Ω的支持度增加，从而减弱了冲突数据对合成结果的影响。但应注意，上述修改过程更改了原始数据，应用时存在些许未知的风险。

2.2 新的DS合成公式及其性质

2.2.1 新的合成公式

传统DS合成公式中，当存在冲突数据时，由于分母归一化会导致合成结果准确性下降或合成公式失效。本文提出一种新的合成公式，基本思想是去掉合成公式中归一化操作，引入证据的一致度和冲突度，并将两者按照各假设的信任分配值大小分配给该假设。该合成公式的优点是可减小证据的不确定性，并减小冲突数据对合成结果的影响，鲁棒性强。新的合成公式为：

(21)

Δρ(A)=s(A)e-CH

(22)

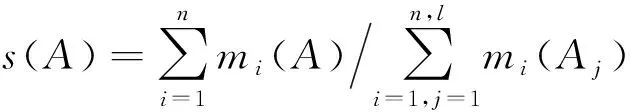
引入一致度和冲突度的依据为：式(22)中e-CH表示了全体SU的感知结果的可靠程度，将此定义为一个待分配值，可以有效表示整体感知数据的可靠情况。利用各假设所占权重s(A)来分配这个待分配值，这样做可以保证公平分配且各假设融合出来的数据不为0，也就避免了证据悖论问题的产生。

利用式(21)和式(22)可得出合成结果m(H1)、m(H0)和m(Ω)。为了使合成结果满足基本概率分配函数的要求，对合成结果作归一化处理，可以得到：

(23)

比较mnor(H1)和mnor(H0)大小进行最终判决，

(24)

以上为该算法的整体步骤。该算法对冲突数据进行了2次修正，来保证冲突数据的可靠性。但是增加了报告信道的传输数据量。也就是说，该算法是以增加传输数据量来保证检测概率的提高。

2.2.2 新合成公式的性质

下面对新合成公式的基本性质进行讨论。

性质1：提出的新合成公式服从交换律。

证明：根据式(21)和式(22)，已知乘法和加法均满足交换律，可得：

m1(Ai)m2(Aj)=m2(Aj)m1(Ai)

(25)

s(m1,m2)=s(m2,m1)

(26)

C(m1,m2)=C(m2,m1)

(27)

H(m1,m2)=H(m2,m1)

(28)

Δρ(m1,m2)=Δρ(m2,m1)

(29)

因此，可以得出新的合成公式满足交换律:

m1⊕m2=m2⊕m1

(30)

以上证明可以说明，使用该合成公式进行融合时，证据体的合成顺序不会影响最终融合结果。

性质2：提出的新合成公式服从结合律。

证明：根据式(21)和式(22)，已知乘法和加法均满足结合律，可得：

s[(m1,m2),m3]=s[m1,(m2,m3)]

(31)

C[(m1,m2),m3]=C[m1,(m2,m3)]

(32)

H[(m1,m2),m3]=H[m1,(m2,m3)]

(33)

Δρ[(m1,m2),m3]=Δρ[m1,(m2,m3)]

(34)

因此，可以得出新的合成公式满足结合律：

(35)

同理，当3组以上的证据进行融合时，也满足结合律。

以上证明可以说明，当多组证据使用该合成公式进行融合时，可进行多次分组融合，每个证据体参与顺序不会影响最终融合结果。

3 仿真分析

3.1 算法鲁棒性的仿真分析

遇到干扰，感知用户的BPA值会发生变化，若合成结果仍保持主焦元不变，则说明该算法的鲁棒性良好。

例：假设在3个感知节点的协作频谱感知系统中，识别框架为Θ={H1,H0,Ω}，得到的证据体为m1、m2和m3，其BPA值如表1所示。

表1 3个感知节点的BPA值Table 1 BPA data of three sensing nodes

在表1中，可以看到证据体m1与m2对H1假设的BPA值最大，H1为证据体m1和m2的主焦元。证据体m3中存在变量x，x∈[0,1.0]。当x=1.0时，H0假设变为证据体m3的主焦元，与前2组证据体产生冲突。下面将本文方法与其他学者的合成方法比较，通过仿真分析来验证表1中证据体的融合结果。

图2为7种改进合成规则的方案与本文方案的仿真对比曲线。从图2中可以看到，在图(a)、图(b)和图(c)中，当x=1.0时，H1假设的BPA值变为0，合成结果出现仅第3个感知节点决定最终融合结果的现象，并且图(b)中的信息不确定性随x的增加而明显增大。图(d)和图(e)随着x的逐渐增大，H0假设的支持度超过了H1假设，主焦元发生改变，并且图(d)中证据的不确定性逐渐增加。图(f)、图(g)和图(h)中，始终保持主焦元不变，但是图(h)比图(f)证据不确定性小，图(f)中的2种假设的BPA值都集中在0.2和0.6之间，图(g)中的2种假设的BPA值都集中在0～0.3，均不满足所有假设BPA值之和为1的要求。因此，仿真结果表明，本文方法的鲁棒性较强，有良好的抗干扰能力，对冲突的处理十分有效。

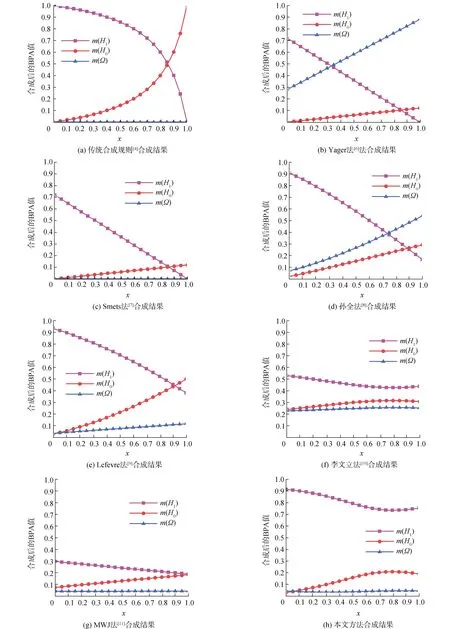
图2 8种合成规则的仿真分析曲线Fig.2 Simulation analysis curve of 8 combination rules

3.2 算法检测性能的仿真分析

假设协作频谱感知的仿真系统中有12个感知用户、1个主用户和1个融合中心。网络场景设置如表2所示，也可参考文献[20]中的网络场景。

表2 网络场景说明Table 2 Description of network scenario

本文采用城市场景下的HATA模型作为路径损耗模型的网络环境。其模型[21]为：

α(hr)+(44.9-6.55lg(ht))lg(d)

(36)

α(hr)=(1.1lg(fc)-0.7)hr-(1.56lg(fc)-0.8)

(37)

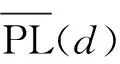
本文仿真参数设置可参考文献[20]和文献[22]。其中ht=100 m，hr=1 m。噪声功率为-106 dBm，对数正态阴影路径损耗模型和噪声的方差σ=σ0=11.6，有效全向辐射功率(effective isotropic radiated power, EIRP)为35 dBm。静态权重的比例系数λ=0.5。能量检测采样点数N=512。蒙特卡洛仿真次数为10 000次。本文方法与其他学者方法对比的具体方案如表3所示。根据文献[23]中证据悖论的种类，本节将针对0信任悖论、1信任悖论和全冲突悖论这3种证据悖论依次进行算法的仿真对比分析。

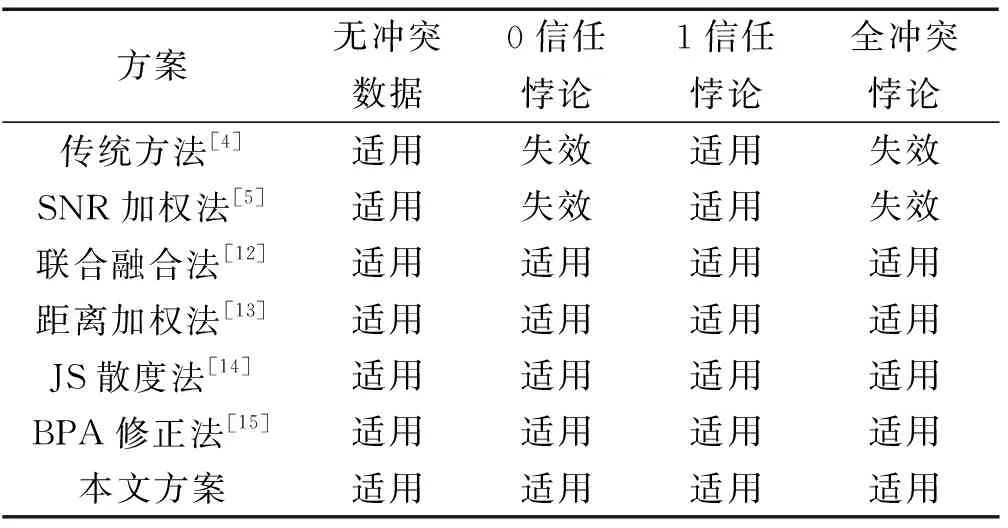
表3 仿真方案说明Table 3 Description of simulation scheme

图3为表3中列出的方案在无冲突数据情况下的检测性能对比曲线。从图3中可以看出，在无冲突数据时，SNR加权法的性能要好于本文方案。并且可以看出，相比于传统方法，修正证据源可以有效提高检测性能。

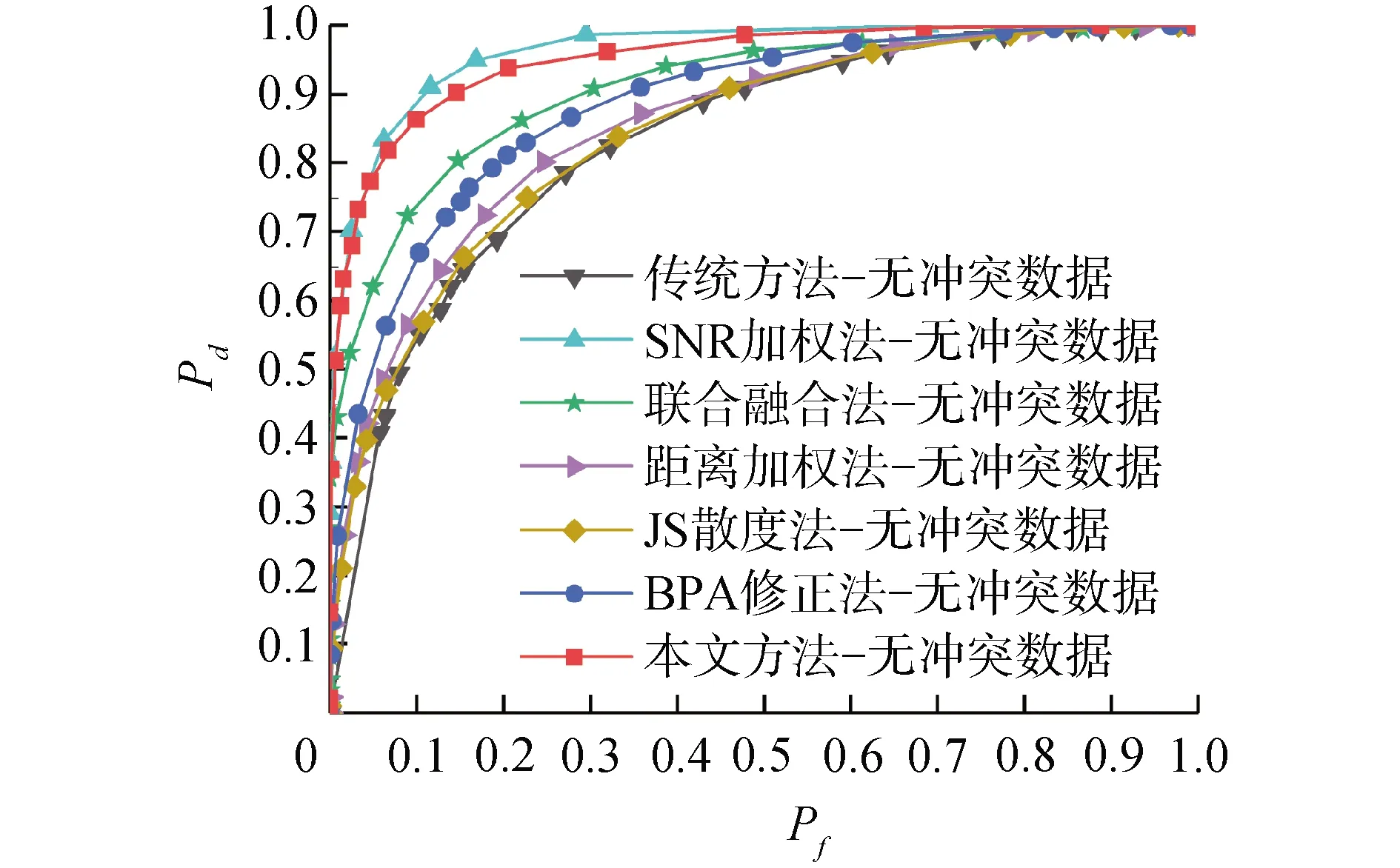
图3 几种方案的检测性能对比-无冲突数据 Fig.3 Detection performance comparison of several schemes-no conflict data

图4为表3中列出的方案在0信任悖论情况下的检测性能对比曲线。

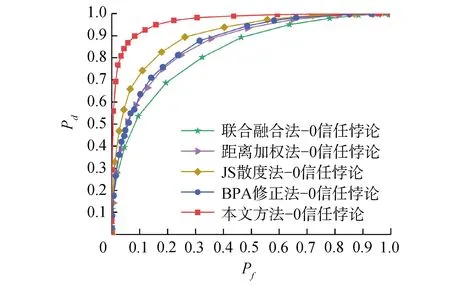
图4 几种方案的检测性能对比-0信任悖论 Fig.4 Detection performance comparison of several schemes-0 trust paradox

从图2(a)中已知，在存在0信任悖论时，传统合成规则会失效，因此传统方法和SNR加权法在0信任悖论情况下完全失效。从图4中可以看出，与无冲突数据的情况下相比，联合融合法性能下降约15%，距离加权法和BPA修正法性能几乎不变，JS散度法性能提升约13%，本文方案性能提升5%且检测性能明显高于其他方案。

图5为表3中列出的方案在1信任悖论情况下的检测性能对比曲线。从图5这几种仿真方案可以看出，1信任悖论只会影响检测性能，不会造成合成公式失效的问题，原因是在图1的系统模型中，识别框架中Ω的定义可以减弱1信任悖论对合成公式的影响。从图中可以看出，除本文方法和SNR加权法，其余方案性能均几乎重合。相比于图3，SNR加权法性能下降约5%，本文方案性能保持不变。

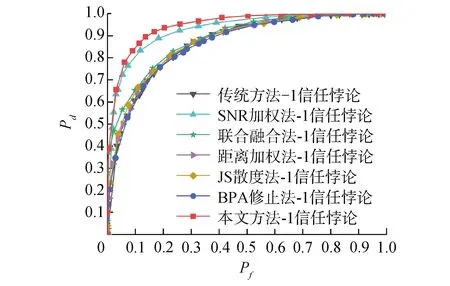
图5 几种方案的检测性能对比-1信任悖论 Fig.5 Detection performance comparison of several schemes-1 trust paradox

图6为表3中列出的方案在全冲突悖论情况下的检测性能对比曲线。全冲突悖论会导致传统方法和SNR加权法融合完全失效。对比图3中各方案的检测性能，联合融合法检测性能下降幅度最大，约为13%，本文方案检测性能提升约5%且整体性能明显高于其他方案。

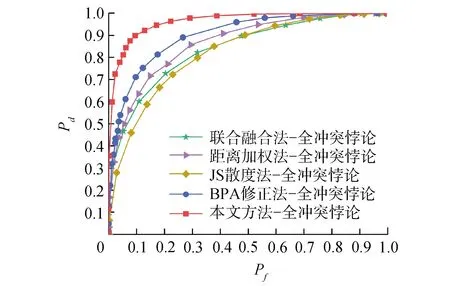
图6 几种方案的检测性能对比-全冲突悖论 Fig.6 Detection performance comparison of several schemes-total conflict paradox

4 结论

1)本文针对证据悖论问题，提出基于证据预处理的协作频谱感知方法。该方法仅对冲突数据进行修正，避免了修正原始非冲突数据带来的风险，并且提出一种新的合成公式，减少不确定性信息的影响。

2)仿真结果表明，相比于其他方法，本文方法检测性能高，鲁棒性强，可以较好地解决证据悖论问题。

3)该方法的局限性在于只适用于故障感知用户少于正常感知用户的情况。

在深衰落、阴影和恶意干扰等更加糟糕的无线信道中，会出现故障感知用户多于正常感知用户的情况，如何确保协作频谱感知方法的有效性和鲁棒性，将作为下一步有待研究探索的工作。