一种基于神经网络的图像加密算法
黎 学 军, 苗 苗, 李 庆 宇, 刘 俊 俏
( 1.大连工业大学 信息科学与工程学院, 辽宁 大连 116034;2.陆装沈阳军代局驻大连地区军代室, 辽宁 大连 116033 )
0 引 言
随着多媒体技术的飞速发展和互联网的普及,数字图像在军事、医学、工业工程、公共安全、商标保护等领域得到了广泛的应用[1],数字图像通过多种平台或信道进行存储和传输[2]。由于图像往往带有私人或敏感信息,因此图像安全问题受到越来越多的关注[3]。
传统的图像加密方法通常是将数字图像视为二进制数据序列,然后使用传统的数据加密技术(如AES[4])对数据序列进行加密。由于,数字图像中的每个像素通常使用至少8 bit来表示,并且相邻像素之间存在较高的信息冗余[5],所以传统的加密算法并不适合用于图像加密。而混沌具有初值敏感性、不可预测性和遍历性等特性,这些特性使得混沌系统产生的伪随机序列非常适用于图像加密[6]。目前,研究者利用忆阻器系统[7]、混沌理论[8-10]、量子理论[11-12]、压缩感知[13-15]、DNA编码[16-17]等技术,设计了多种图像加密算法。例如,Chen等[18]提出了一种基于改进混沌映射的自适应医学图像加密算法,利用logistics混沌映射对平面图像进行置乱处理,同时采用超混沌系统对子块进行自适应加密。文献[19]中提出了一种基于混沌映射和动态模曲线的图像加密解密算法,利用射影变换提高了算法的扩散性。Chai等[20]基于纯图像和拉丁方阵(PPILS)的置换和双向自适应扩散。提出了一种具有高自适应性的医学图像加密方案,文献[21]中提出了一种基于隐藏吸引子混沌系统、Knuth-Durstenfeld算法和DNA序列操作的图像加密方案,利用隐藏吸引子混沌系统生成图像加密所需的混沌序列。文献[22]中提出了一种基于扩散过程和改进的Playfair密码的图像加密算法,利用混沌交叉映射对各图像颜色通道的矩阵进行置换和扩散处理。Niu等[23]提出分数阶混沌系统的反控制,并应用于彩色图像加密。文献[24]中提出了一种基于混沌的并行图像加密方案。文献[25]中提出了一种基于左卡普托离散增量的三维分数阶离散Hopfield神经网络(FODHNN),研究了该神经网络的动态特性和同步特性,并将其应用于图像加密。Zhang等[26]提出了一种基于整数域的类感知器网络的图像加密方案,以感知器网络为核心,实现普通图像的信息存储和传播。Liu等[27]基于菲涅尔域的双随机相位编码,提出了一种基于超混沌系统和公钥密码理论的光学图像加密算法。
与传统的混沌系统相比,激光混沌系统不仅有各种各样的耗散系统的复杂现象,同时具备双稳态、接近理想模型、容易设计等特性,使得激光混沌系统在混沌密码学有很好的应用潜力[8]。因此,本研究采用单模激光混沌系统生成像素置乱和扩散的伪随机序列,与神经网络方法与Arnold置乱方法、加取模操作扩散方法结合,设计了一个新型的数字图像加密方案。
1 单模激光系统
1.1 单模激光Lorenz系统
单模激光Lorenz系统的动力方程为
(1)
式中:a,b,c是系统参数。令初值x0=1,y0=2,z0=3;参数a=10,b=8/3,c=30;步长h=0.01。计算得到系统的李雅普诺夫指数LEs=(1,0,-14.79),其中,有一个正的李雅普诺夫指数,并且所有的李雅普诺夫指数和为负,所以单模激光Lorenz系统是混沌系统,系统相图如图1所示。
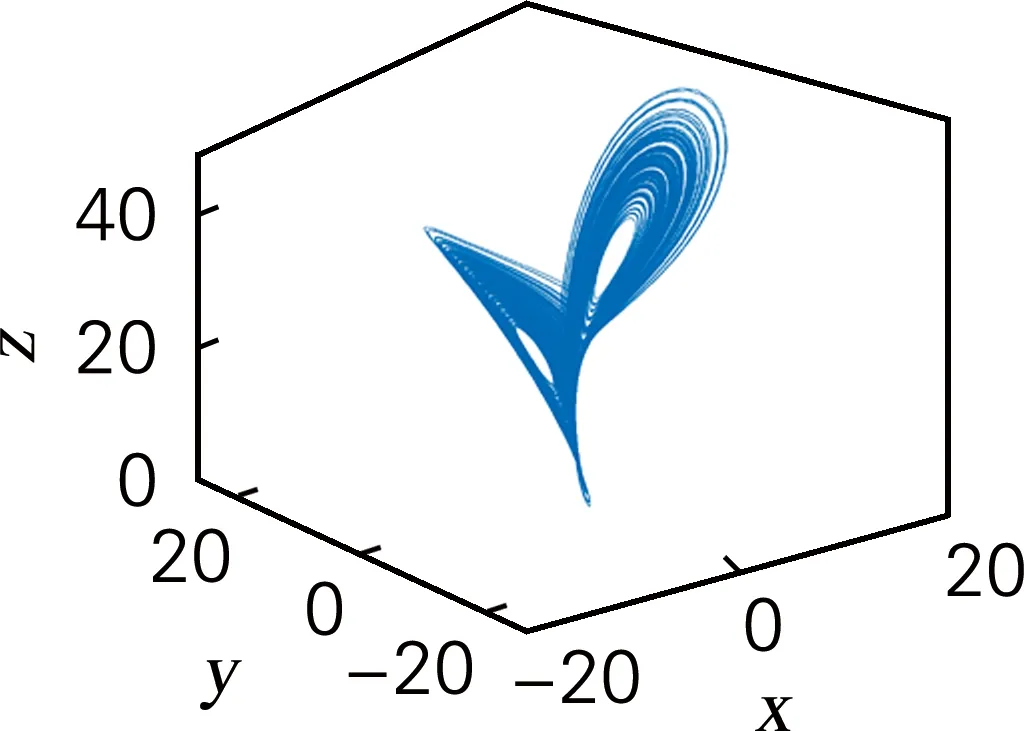
(b) x-y-z空间相图
1.2 系统不同参数对动力性能的影响
令系统b=8/3,c=30,h=0.01;初始值x0=1,y0=2,z0=3。当a∈[4,23]时,系统的分岔图、李雅普诺夫指数谱和SE复杂度如图2所示。由图2(a)、(b)可知,当a∈(4.0,5.2)∪(22.18,23.00]时,系统李雅普诺夫指数均小于0,系统处于稳定状态;当a∈(5.20,22.17)时,有一个正的李雅普诺夫指数,系统处于混沌状态。图2(c)表明系统处于混沌态时复杂度较大,当系统处于稳定状态时,SE复杂度很小,甚至接近于0。
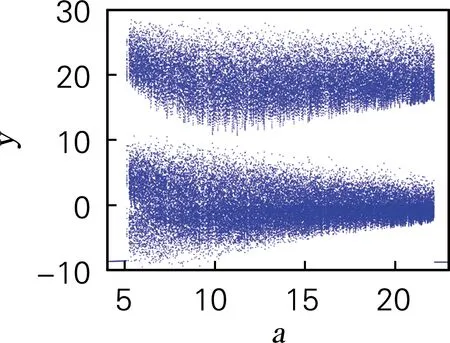
(a) 分岔图

(b) 李雅普诺夫指数谱
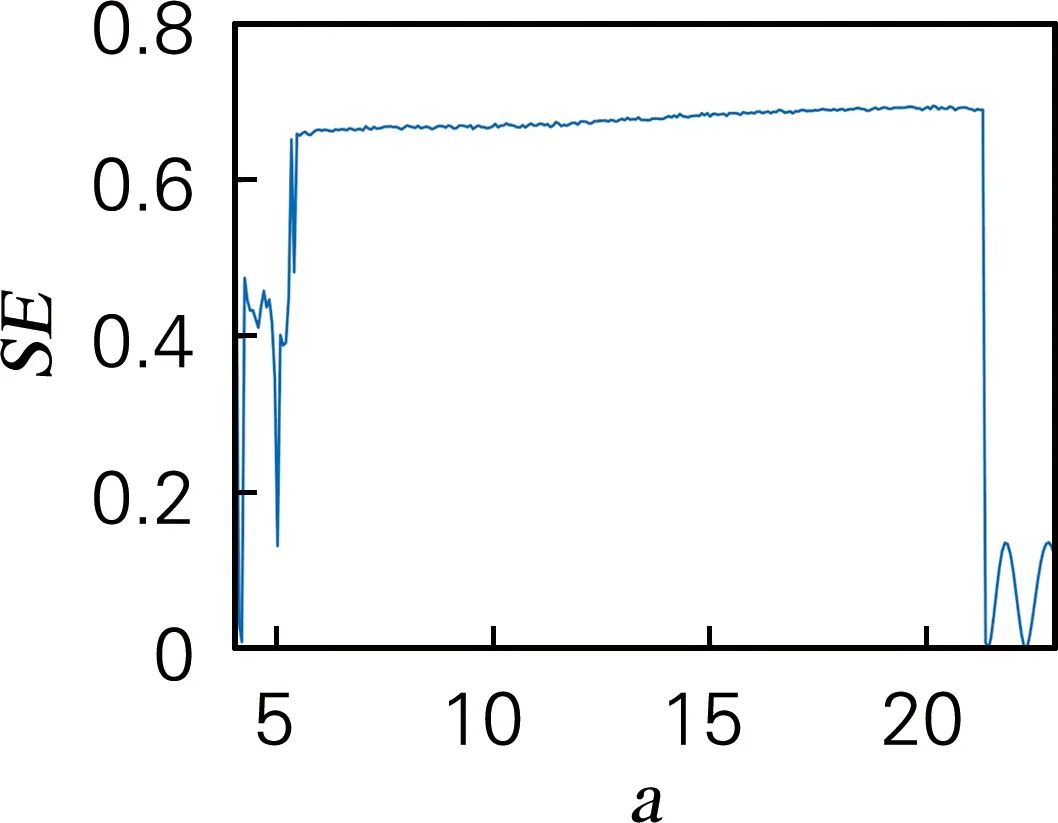
(c) SE复杂度图2 系统在参数a∈[4,23]时的分岔图、李雅普诺夫指数谱和SE复杂度Fig.2 Bifurcation diagrams, Lyapunov exponents spectra and SE complexity diagram of the systemwith parameter a∈[4,23]
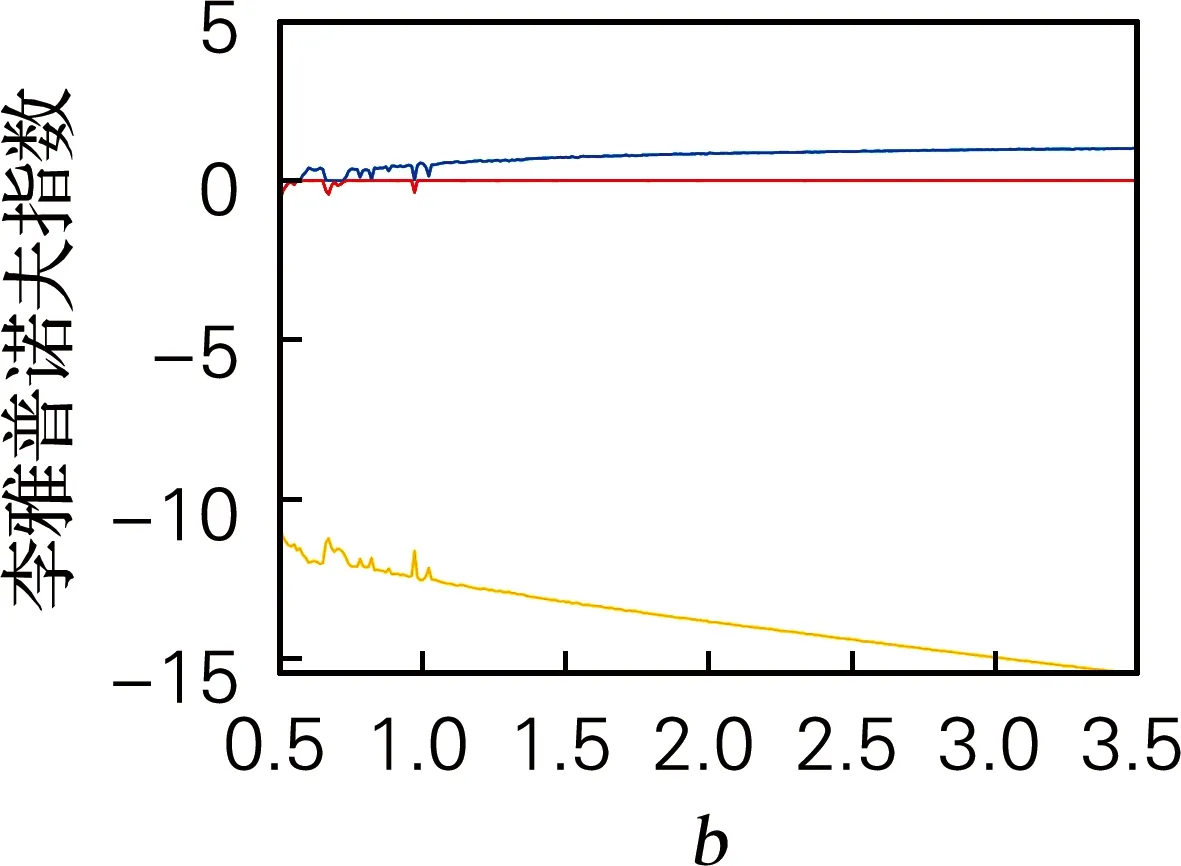
令参数a=10,c=30,h=0.01,系统初始值x0=1,y0=2,z0=3;当b∈[0.5,3.5]时,系统的分岔图、李雅普诺夫指数谱和SE复杂度如图3所示。图3(a)~(b)中,当b∈[0.50,0.58)∪(0.65,0.73)∪(0.96,0.98)时,最大李雅普诺夫指数为0,系统表现为周期运动形式,并且系统在b为0.54和0.73处出现倍周期分岔;当b∈(0.58,0.65)∪(0.73,0.96)∪(0.98,3.50)时,有一个正李雅普诺夫指数,系统处于混沌状态。图3(c)表明在混沌状态区间复杂度较大,与分岔图和李雅普诺夫指数谱的状态一致。
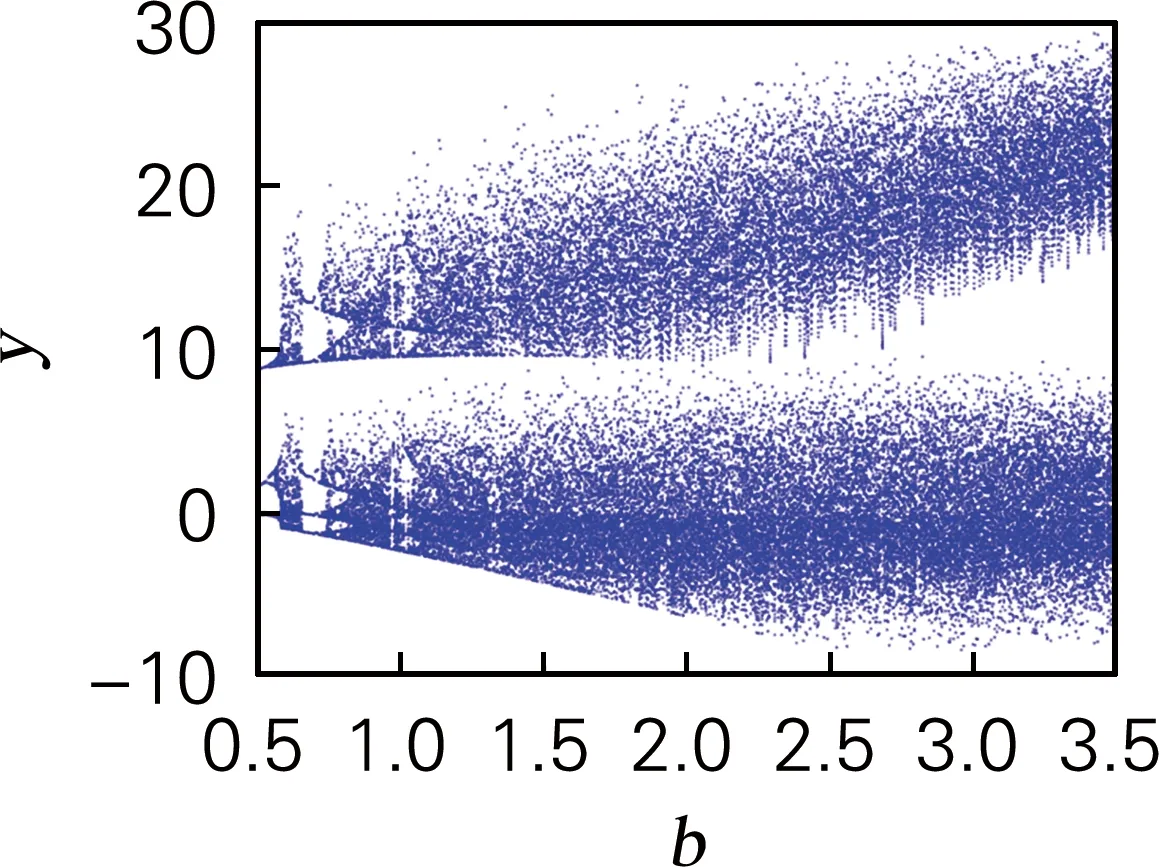
(a) 分岔图
(b) 李雅普诺夫指数谱
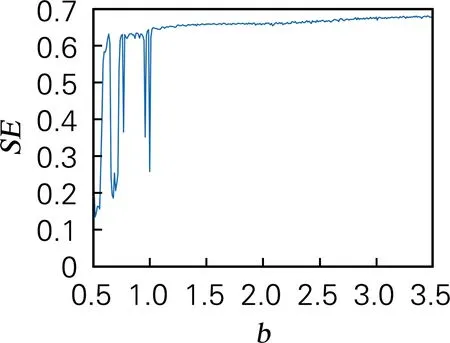
(c) SE复杂度图3 系统在b∈[0.5,3.5]时的分岔图、李雅普诺夫指数谱和SE复杂度Fig.3 Bifurcation diagrams, Lyapunov exponents spectra and SE complexity diagram of the systemwith b∈[0.5,3.5]
2 加密与解密算法设计
2.1 Arnold变换
Arnold变换也称“猫变换”,是一种在有限区域内进行反复折叠、拉伸变换的混沌映射方法[12]。数字图像可看作一个二维矩阵,图像中的像素位置可看作二维矩阵中对应坐标的位置。经过Arnold变换,图像的像素位置会重新排列,实现对图像的置乱加密效果。Arnold变换算法(正变换)由式(2)实现。
(2)
式中:αn和βn为变换前图像像素的位置,αn+1和βn+1为变换后像素的位置,p和q为当前变换的次数,N为图像的长或宽,mod为模运算。
Arnold变换的逆变换为
(3)
两个变换矩阵为互逆矩阵,且逆矩阵仍然是整数矩阵。
2.2 BP神经网络
BP神经网络模型主要由层(包括输入层、隐含层和输出层)、神经元和神经元之间的权值三部分组成。输入层神经元接收输入信息,并传输给隐含层的各神经元,隐含层神经元负责对接收的信息进行处理变换,由输出层输出处理结果。各层神经元仅与相邻层神经元全连接,同层神经元无连接。图4为BP神经网络方法中各神经元的计算过程。输出层的神经元产生网络的初始结果,输入与输出之间的计算过程可以表示为
(4)
式中:I和H为输入层和隐含层神经元数量,Xi为输入信息,bj、bk分别为隐含层偏差和输出层偏差,foutput和fhidden分别为隐含层神经元和输出神经元的传递函数,wji为连接输入层和隐含层的权值,wkj为隐含层与输出层之间的权值。
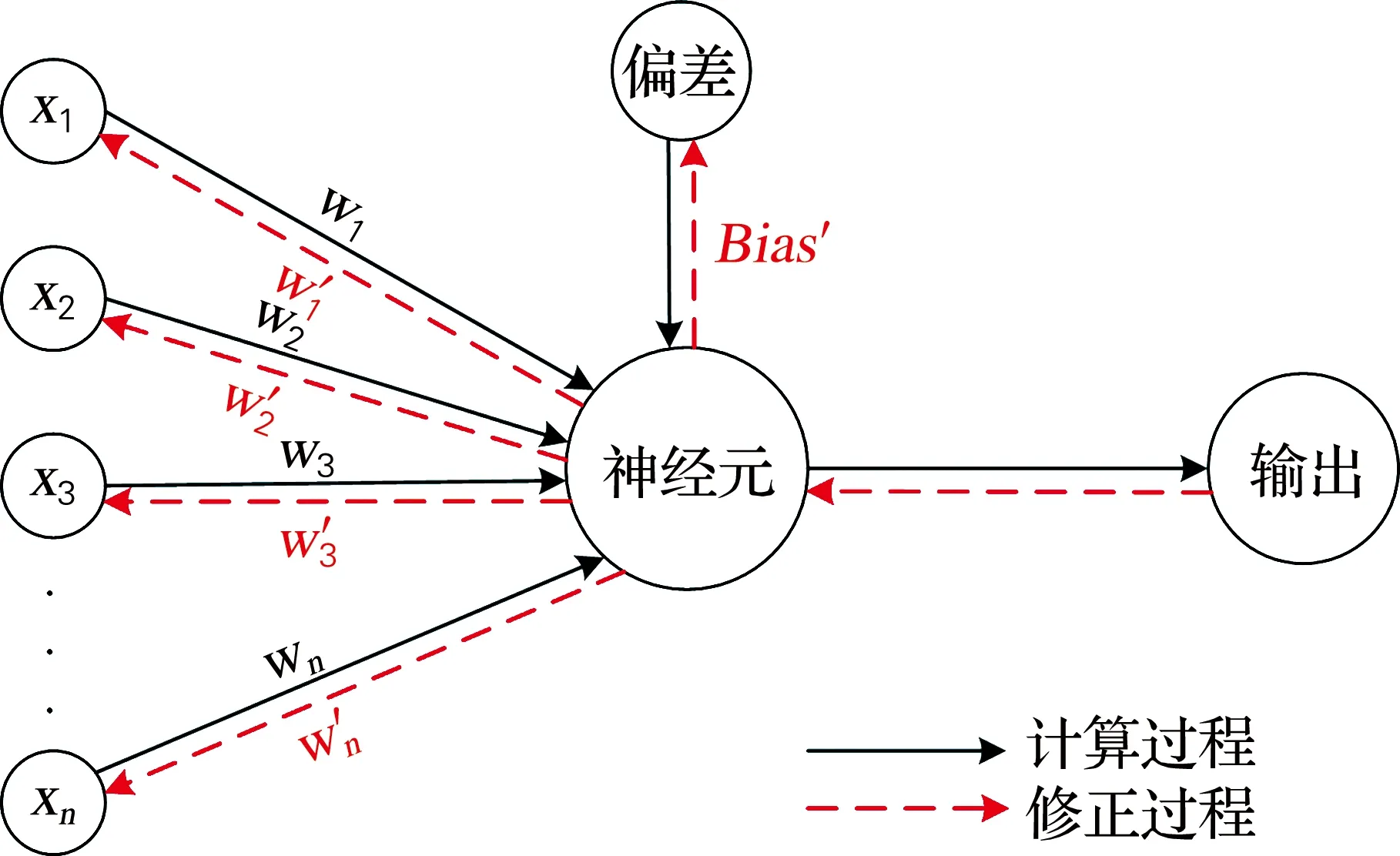
图4 神经元计算原理Fig.4 Principles of neurocomputing
通过式(5)测量输出值与实际值之间的误差,如果误差超过公差,则通过梯度下降法修正权值和偏差。通过修改后的权值和偏差对输出值进行再训练,重复上述过程,直到输出在公差范围内。
(5)

2.3 加密算法
假设输入的图像大小为W×H,所提出的图像加密流程如图5所示。
具体的加密算法步骤:
步骤1输入图像IW×H,对输入图像的所有像素点进行分割,将W×H的图像分割成N
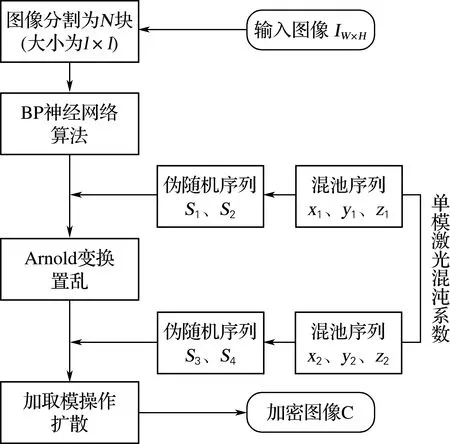
图5 加密流程Fig.5 Encryption process
个子图像块,每个图像块的大小为l×l。
步骤2对生成的子图像块矩阵进行归一化处理,并采用均值分布预处理。待处理图像的灰度范围为[xmin,xmax],变换域为[ymin,ymax],假设要处理的像素为xvalue,yvalue可由式(6)得到。
(6)
原始图像的像素值通过式(6)划分为[0,1]的集合,构成所有训练样本的预处理过程。
步骤3BP神经网络的输入为图像数据样本,如果BP神经网络的压缩率为k,则网络的输入层节点数为ni,隐藏层的节点数为nk,即k=ni/nk。当神经网络被训练时,网络的耦合权值在压缩过程中保持不变。
步骤4利用newff函数进行训练,可得到压缩数据,传递函数为
(7)
其中,logsig(n)函数的特点是(-∞,+∞)范围的数据被映射到区间(0,1)内,且n为神经元节点数的输入。
(8)
其中在tansig(n)函数中,输出将被限制在(-1,1)区间内。为了使预测输出和实际输出相差不大,均方差的值应足够小,且考虑加密时间,本算法中设置均方差为0.000 35。
步骤5设置单模激光混沌系统的参数和初值,对混沌系统迭代(t+W×H)次。将前t个值舍去,以提高混沌系统参数和初值的灵敏度。结合得到3个混沌序列x1、x2、x3,得到浮点数类型的伪随机序列S。
步骤6由浮点数类型的伪随机序列K得到整数类型长度为2(W×H)的伪随机数向量X,Xi∈{1,2,…,10(W×H)}。再由X得到两个伪随机序列S1、S2。
步骤7将神经网络压缩后的图像矩阵Q转换为一维向量T,利用伪随机序列S1、S2对T进行置乱。再将一维向量还原为W×H的像素矩阵。
步骤8同理根据第5步和第6步得到伪随机序列S3、S4。
步骤9采用伪随机序列S3、S4对像素值进行扩散操作,扩散算法为Bi=(Bi-1+Si+Pi)mod(256)。其中置乱图像展开为P,S为密码向量,对应密文为B,i=1,2,3,…,W×H。
Bi=(Bi-1+Si+Pi)mod(256)展开为
Bn=(B0+S1+S2+…+Sn+P1+
P2+…+Pn)mod(256)
(9)
正向扩散为
Bi=(Bi-1+Si+Pi)mod(256)
(10)
逆向扩散为
Pi=(2×256+Bi-Bi-1-Si)mod(256)
(11)
步骤10根据式(9)~(11)可得到密文向量B,然后将其恢复为像素矩阵,最后得到加密图像C。
2.4 解密算法
图像的解密过程是图像加密的逆过程,解密流程如图6所示。具体的解密步骤:
步骤1读取加密图像C,根据加密算法的第8步,得到逆过程的伪随机序列S3和S4。
步骤2由式(12)和式(13)对像素值进行恢复,得到像素矩阵E。
正向扩散为
Bi=(Bi+1+Si+Pi)mod(256)
(12)
逆向扩散为
Pi=(2×256+Bi-Bi+1-Si)mod(256)
(13)
步骤3根据加密算法的第5和第6步,得到逆过程的伪随机序列S1、S2,结合Arnold逆变换算法,对逆扩散后的像素矩阵进行像素位置的恢复,得到一维向量F。
步骤4将一维向量F的像素值从[0,1]恢复到[0,255],向量被恢复为l×l的子图像块。
步骤5将所有的子图像组合成一个完整的图像即可得到解密图像。
3 算法测试结果与性能分析
3.1 算法测试结果
选择256×256的灰度图像作为对象对算法性能进行分析。由本文算法得到的明文图像、密文图像和解密图像如图7所示。从图像加密的结果可知,加密效果良好,可以有效掩盖明文图像中的信息。同时,解密算法可以完全正确解密密文。由于图像加密安全性能的好坏直接决定算法能否有效抵御外部攻击,因此加密效果需要使用密钥敏感性、直方图分析、相关分析、信息熵、NPCR、UACI、鲁棒性分析等进行安全测试。
3.2 密钥空间
密钥空间是指所有合法密钥构成的集合,图像密码系统的密钥空间应该足够大,从而可以有效地对抗穷举攻击,密码长度至少应该为128 bit[29]。在本算法中,密钥约为292 bit,所以密钥空间大约是2292。从表1与其他加密算法比较可以看出,本文算法的密钥空间大小足够大,可以抵御所有类型的穷举攻击。
3.3 密钥的敏感性分析
有效的图像加密算法应该对加密阶段和解密阶段密钥的细微变化非常敏感,密钥的细微变化,加密效果会有很大的不同。这种不同的程度可以通过计算两幅不同的密文的差值来评价。本算法中,对密钥a、b和c进行灵敏度分析,当参数产生了10-15的微小改变时,新的密文图像和与原始密文图像之间的差异如图8所示。从图8可以看出,当参数发生微小改变时,所得到的密文图像与原始密文之间存在差异,表明本文加密算法的密钥具有确定性和唯一性。
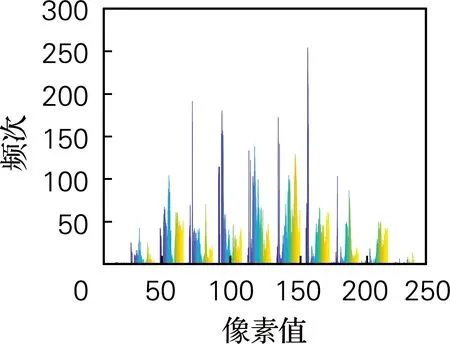
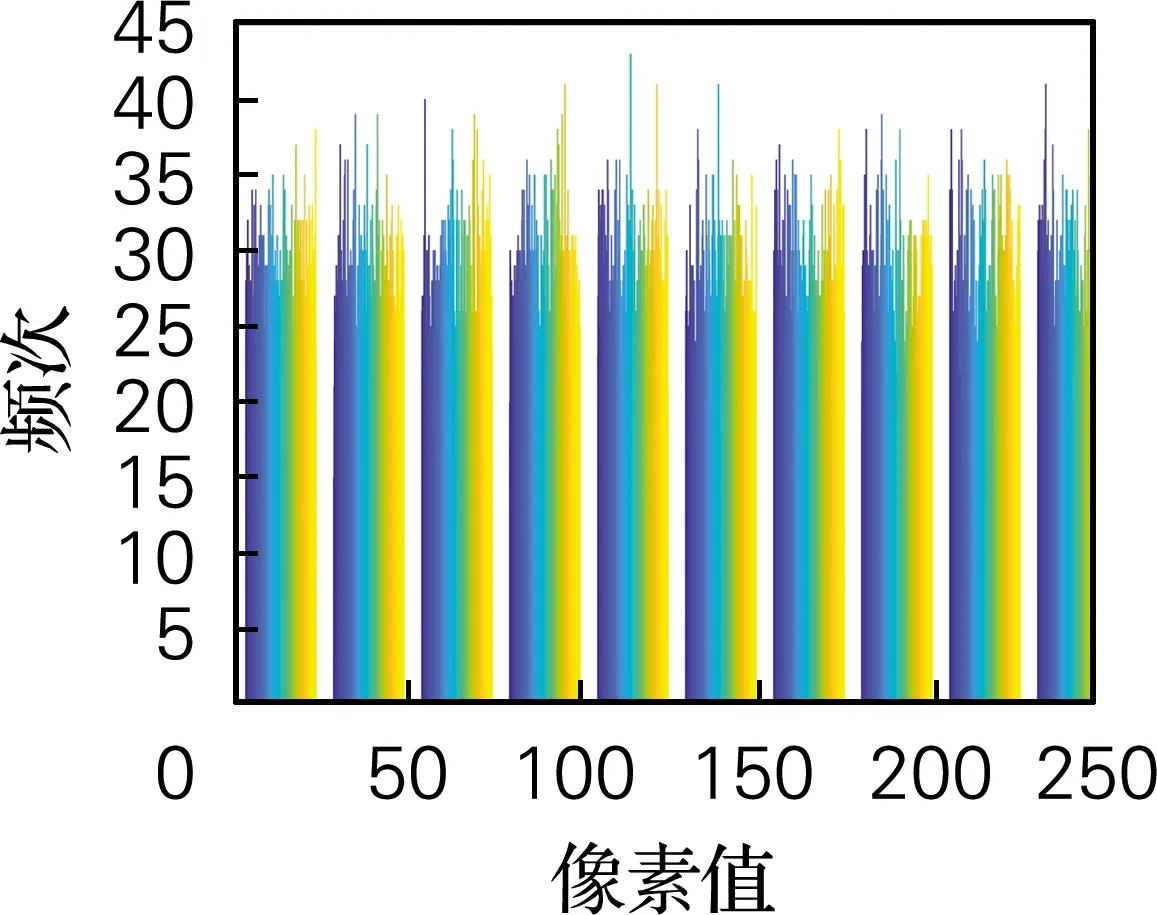
3.4 直方图分析
直方图表示像素点的分布情况。相对于明文图像的直方图,理想加密图像的像素分布应该是均匀的、平坦的,它有效地隐藏了平面图像的像素值,以防止攻击者提取有效信息。从图9的实验结果可以看出,明文图像的直方图并不平坦,也就是说,图像中包含像素的关键信息,不能有效地抵抗攻击者提取图像的关键信息。而使用本文算法加密的图像直方图分布比较平坦,较好地隐藏了图像的关键信息,可以有效抵抗统计攻击。
3.5 相关性分析
相关性反映了相邻像素之间的相关程度。在加密算法中,常对相邻像素的线性关系进行测试。一般情况下,明文图像的相邻像素具有较高的相关性,抗差分攻击能力较弱;而密文图像极大地消除了相邻像素之间的相关性,大大提高了图像的抗差分攻击能力。利用式(14)可以计算出相邻像素在水平、垂直和对角方向上的相关性。

原始密文图像

密文图像

密文差异

原始密文图像

密文图像

密文差异

原始密文图像

密文图像

密文差异
(a) 明文图像
(b) 密文图像
(14)
式中:x、y为相邻两个像素的灰度值。图10为Lena明文图像与密文图像在水平方向、垂直方向和对角方向的相关系数。由图10的实验结果可知,密文图像相邻像素的相关系数大大降低。为了进一步展示相关系数的特征,相关系数的比较结果如表2所示。从表中可以看出,应用本文算法加密图像,密文图像的相关性更低,具有更好的抗攻击性能。
3.6 抗差分攻击分析
由于图像加密算法的精度很高,使得平面图像中像素的微小变化都会导致加密效果发生巨大变化。这种变化通常通过像素改变率(NPCR)和归一化平均变化强度(UACI)来测量,体现了加密算法的抗差分攻击能力。其定义为
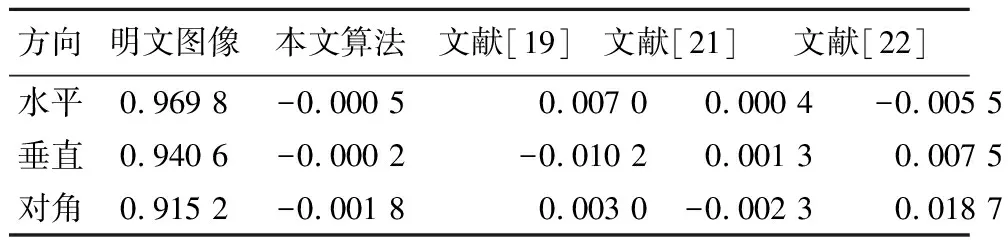
表2 Lena相关系数的比较Tab.2 Comparison of Lena correlation coefficients
(15)
式中:c1,c2为两幅大小为W×H图像。当c1(i,j)≠c2(i,j)时,可得D(i,j)=1。如果c1(i,j)=c2(i,j),则D(i,j)=0。NPCR的期望值为99.6094%,UACI的期望值为33.4635%。通过表3与不同算法的对比可以看出,本文算法具有更好的抗差分攻击性能。
3.7 信息熵
信息熵反映了图像信息的不确定性,是测试加密算法安全性的一种常用方法。具体算法为
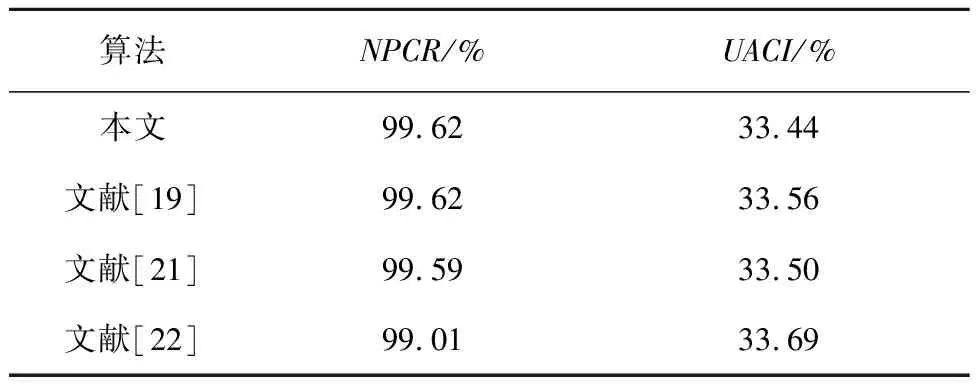
表3 UACI和NPCR的平均值Tab.3 Average values of UACI and NPCR
式中:p(si)是si的概率。对于256阶的灰度图像,理想信息熵为8。信息熵值越接近8,图像可视信息越少,像素点的分布越接近随机。从表4中Lena图像的对比结果可以看出,本文算法的信息熵接近理想值,具有很高的安全性。
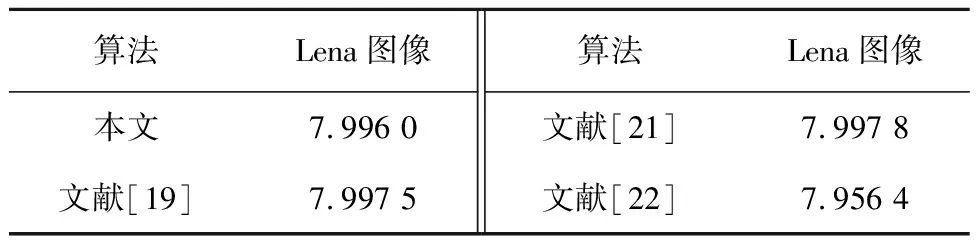
表4 信息熵的比较Tab.4 Comparison of information entropy
3.8 鲁棒性分析
在数字图像的传输和存储中,容易产生不同类型的噪声和数据丢失,因此一个好的加密算法应该能够有效抵抗密文图像的失真。数据丢失攻击和噪声攻击常用于测试图像加密算法的鲁棒性。图11(a)~(d)显示了椒盐噪声攻击(SPN)的Lena加密图像和解密图像,图11(e)~(h)显示出了数据丢失(DL)的Lena密文图像及其解密图像。当加密图像丢失一些数据或被噪声模糊时,解密过程仍能恢复原始图像,且具有很高的视觉效果。实验结果表明,该加密算法能够有效抵抗噪声和数据丢失攻击,具有很好的鲁棒性。
4 结 论
所提出的基于激光混沌系统与神经网络的图像加密算法,利用激光混沌系统对初始条件的敏感性增加了秘钥空间及其敏感性,并结合BP神经网络对加密图像进行压缩和Arnold变换有效降低图像相邻像素的相关性,提高了算法抵抗统计和敏感性攻击的能力。通过与其他加密算法在安全性上的比较分析,可以看出所提出的算法具有很高的安全性。因此,该算法适合于图像加密,以保护数字图像信息在互联网上的安全传输,具有较好的实用意义和应用前景。

(a) 密文图像(SPN=1%)

(b) 解密图像(SPN=1%)
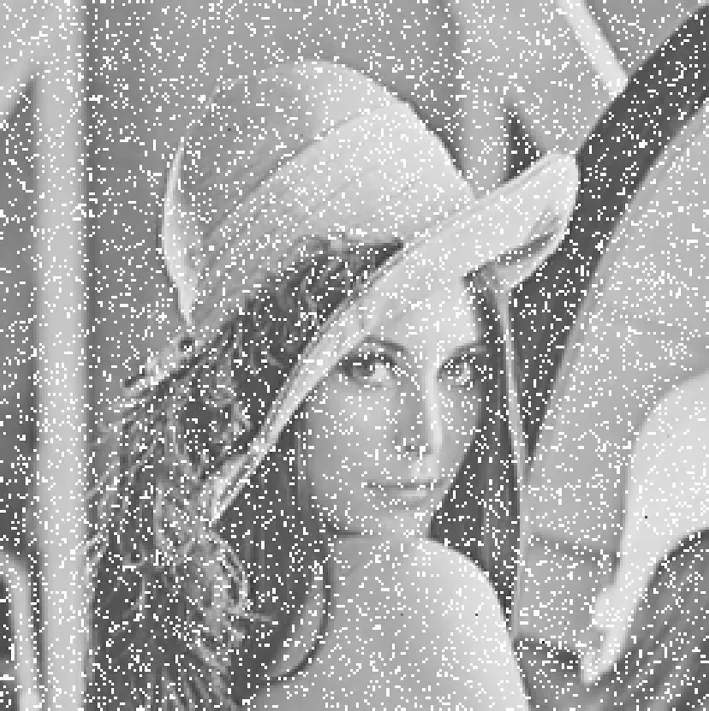
(d) 解密图像(SPN=4%)

(e) 密文图像(DL=3%)

(f) 解密图像(DL=3%)

(g) 密文图像(DL=10%)
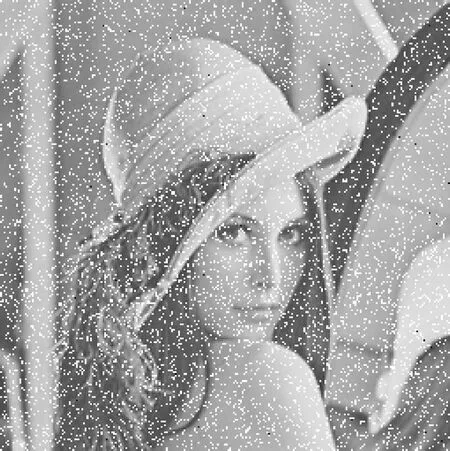
(h) 解密图像(DL=10%)

