公路运输振动环境下发动机粘接界面 受载情况分析

徐伯起，卢明章，李高春，李金飞，王玉峰

（1.海军航空大学 岸防兵学院，山东 烟台 264001； 2.中国人民解放军91049部队，山东 青岛 266102）

固体火箭发动机广泛应用于海军各种型号的导弹中。目前研究表明，推进剂与衬层粘接界面的粘接破坏是固体发动机结构完整性破坏的关键形式之一。纵观导弹全寿命环境[1]，运输阶段的载荷环境极其恶劣。相较于艇载运输过程[2]的振动加速度幅值（≤0.4 m/s2），铁路及舰载运输[3]条件下基本稳定在–0.5 m/s2~0.5 m/s2，公路运输过程中受到的振动载荷更大，并且公路运输会路经荒山、沿海等复杂地形，导弹所受振动载荷会更加复杂。为了保证导弹运输过程中的安全稳定，对公路运输中粘接界面受载情况进行分析意义重大。

目前研究人员对于振动载荷分析主要从时域和频域两方面进行[4-6]，大多基于相关标准进行仿真分析来研究载荷。刘铁[7]通过进行仿真计算导弹运输车，获得不同路况和运输车速时的振动响应情况。李恩奇[8]利用MSC.NASTRAN有限元软件，得到了固体火箭发动机药柱的固有频率、相应的振型、各阶模态损耗因子和频率响应曲线，以及随机振动响应均方根值和功率谱密度曲线。针对粘接界面处受载情况，Herb Chelner[9]和张波[10]等通过在粘接界面处设置传感器研究其受载情况。

基于上述研究，文中利用加速度传感器对导弹公路运输振动载荷进行测量，完成加速度数据的统计分析和PSD的计算。利用有限元软件构建发动机全尺寸模型，通过瞬态模态分析和随机响应分析研究结构的振动响应，输入实测加速度数据模拟发动机实际振动过程，获得粘接界面处所受应力情况，为运输过程中发动机可靠性评估提供数据基础。

1 振动数据处理

1.1 数据采集

公路运输的振动载荷数据采集方法为：在运输车底盘纵向安装型号为1C301型的电容式三向加速度传感器，采样频率为200 Hz，采样时间总长为7.1165 h。传感器传回的三个方向上的振动数据符合笛卡尔坐标系，x轴正向为车辆前进左侧方向，y轴正向为车辆前进方向，z轴正向为竖直向上方向。

实际环境中，各种变化因素使得监测信号发生偏移，即产生趋势项。为还原信号的真实情况，需要对采集到的信号进行相应的预处理。

文中采用多项式最小二乘法的方法进行趋势项的消除[11]。首先对采集到的信号{xi}(i=1,2,… ,n)设置一个多项式函数：

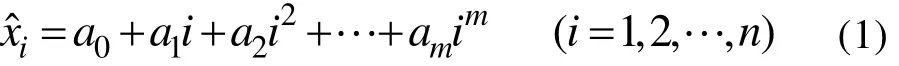
式中：m为多项式阶次；aj(j= 1,2, … ,m)为多项式系数。

E存在极值的条件为其对a求偏导为0：

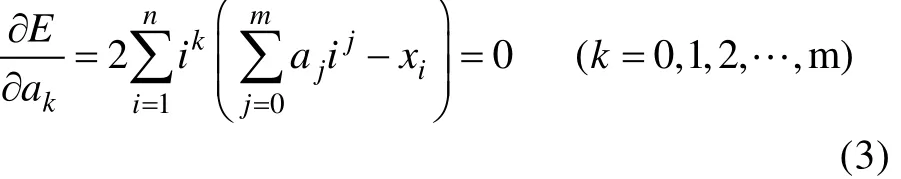
对式（3）变形后得到m+1元线性方程组：

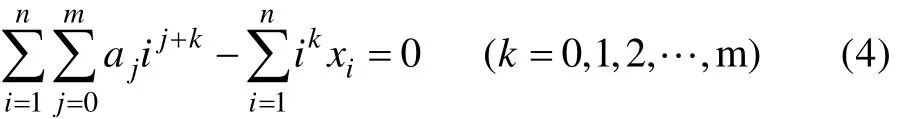
求解式（4）中的方程组，可以得到多项式函数ˆix的系数aj(j= 1,2, … ,m)，阶次m影响多项式的形式。当m=1时，趋势项为线性函数；当m≥2时，趋势项为幂函数。文中m取2。

多项式函数ˆix各项系数确定后，消除趋势项的计算公式为：

图1显示了处理后的信号。对比不同轴向上的振动信号，发现三轴向的振动信号具有相同波形。在幅值上，z轴向最大，对应竖直方向；y轴向最小，对应车体左右侧方向。从时间历程上看，路况较好时，加速度幅值为–0.05g~0.05g；路况较差时，幅值为–0.6g~0.6g。

图1 振动加速度历程 Fig.1 Vibration acceleration history

1.2 时域统计分析

考虑到导弹在运输过程中处于卧式放置的方式及粘接界面结构特点，z轴向载荷对导弹影响最大，因此文中主要研究z轴向载荷。

时域分析是根据载荷的时间历程，计算相关统计特征量进行分析。典型的统计特征量主要包含峰值、均方根值、斜度和峭度。其中斜度[12]表征数据的偏斜方向和程度，是非对称程度的数字特征，计算公式见式（6）；峭度[13]表征概率密度分布曲线在平均值处峰值高低的特征数，计算公式见（7）。

图2a为加速度的统计分布情况，图2b为加速度绝对值的统计分布，表1显示了z轴向信号的特征量。可以看到，信号峰值大于3倍均方根值，说明采集到的振动数据中包含数值急剧变化的部分。斜度和峭度反映的是信号接近于正态分布的程度，标准正态分布的斜度为0，峭度为3。采集信号斜度为–0.46，对应图2a分布曲线稍向右偏；峭度为9.34，属于超高斯分布，说明采集信号中包含冲击信号[14]，对应路况较差的情况。

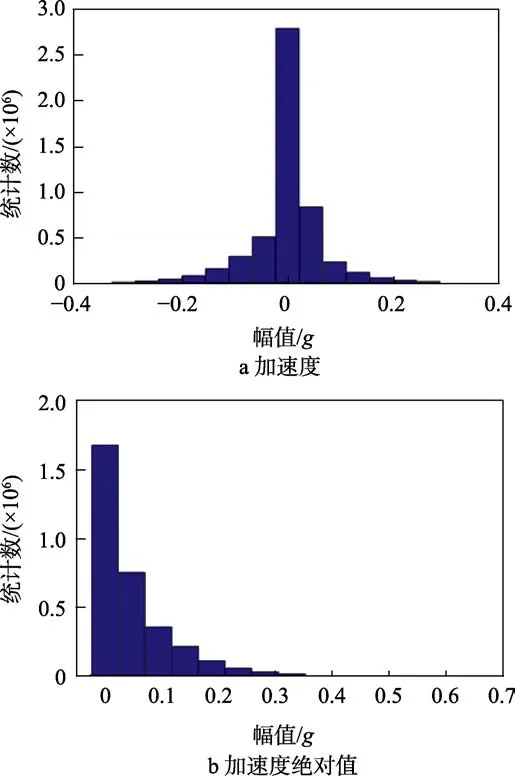
图2 载荷统计分布情况 Fig.2 Value distribution: a) value histogram; b) absolute peak value distribution

表1 信号的特征量 Tab.1 Signal typical statistical characteristic

1.3 载荷谱构建

为了对比分析路况好、坏两种情况下的振动载荷 特点，采用了基于PSD等级对运输条件进行分类的方法[15]。根据国际平整度指数（IRI）[16-17]进行道路状况分类[18]。表2显示了两个振动严重程度级别（A，B）及其PSD级别。依据振动等级，各提取5段A级和B级下的信号段，每段信号时长300 s，包含60 000个数据点。求取各等级下的振动信号段PSD，绘制的10段PSD曲线如图3所示。通过对每个级别内5段信号的PSD进行平均，得到每个振动级别（A、B）的平均PSD。假设采集过程中行驶速度不变，通过计算每个等级下信号时长与总时间的比值，得到各等级PSD在总行程上的比率，A级占41%，B级占59%，以行程占比作为权重，计算等效PSD，如图4所示。

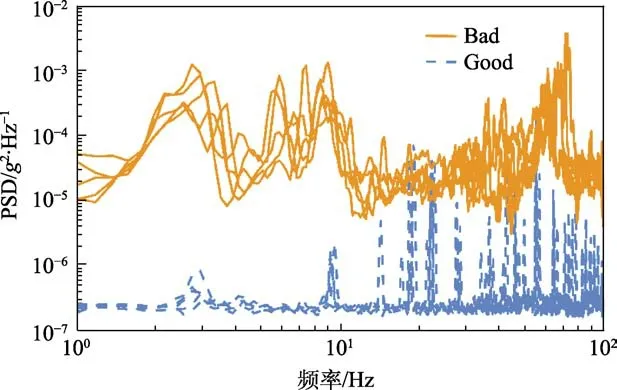
图3 两种振动等级的PSD Fig.3 PSD in two vibration severity classes

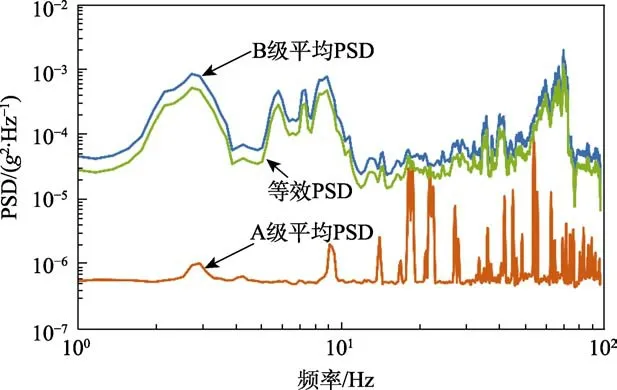
图4 平均PSD与等效PSD Fig.4 Average PSD and equivalent PSD

表2 基于PSD的振动级别划分 Tab.2 Classification of vibration severity based on the PSD level

为方便将PSD输入到有限元软件中进行计算，还需要将PSD转换为倍频程格式，从而简化功率谱密度，同时保证输入载荷谱真实性。简化结果如图5所示。

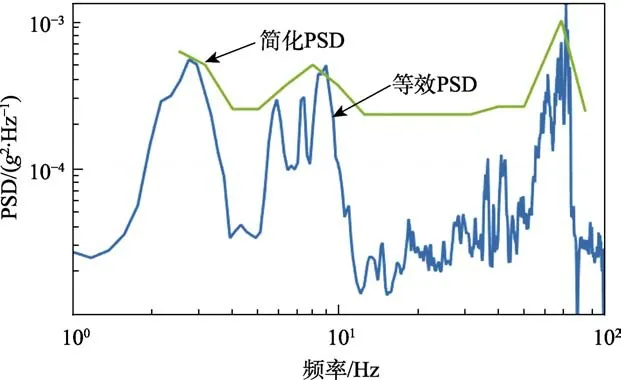
图5 简化PSD Fig.5 Simplified PSD

2 有限元仿真分析

文中利用有限元软件Abaqus构建发动机模型，输入加速度PSD对发动机进行模态分析。利用两个振级下的实测加速度数据，模拟发动机振动过程，获得粘接界面应力历程。

2.1 模型基本参数

导弹发动机的简化模型如图6所示，模型主要由壳体、绝热层、人工脱粘层和推进剂药柱构成，各部件材料参数设置见表3。考虑到药柱的热粘弹特性，采用如式（6）所示的Prony级数形式[19]设置推进剂弹性模量。考虑到实际情况下壳体与衬层、衬层与推进剂、壳体与人工脱粘层界面粘接牢固，将边界条件简化为绑定约束，人工脱粘层和药柱间不设置约束。

表3 各部件参数设置 Tab.3 Parameter setting of each part

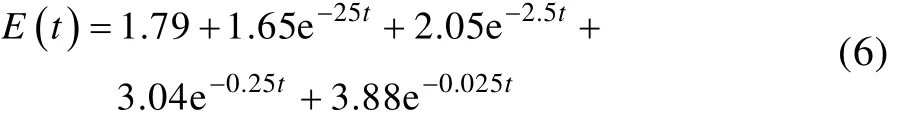
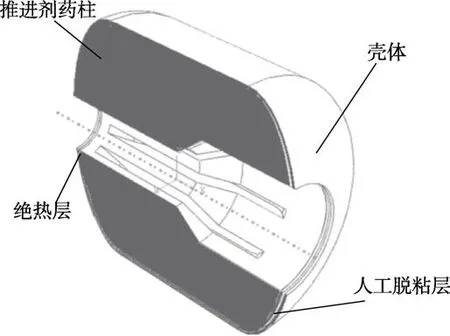
图6 导弹发动机的简化模型 Fig.6 Simplified model of missile engine

设置边界条件情况：在壳体与绝热层接触面和绝热层与药柱接触面上设置绑定约束，人工脱粘层与壳体之间不设约束，用于释放封头处集中应力。在模态分析过程中，封头外表面完全固定。在模拟振动过程时，模型外表面施加y轴向的约束。

2.2 模态分析

利用加速度PSD进行发动机模态分析需设置两个分析步：第一步先进行瞬态模态分析，提取前10阶模态，模型各阶模态频率见表4；第二步输入简化PSD进行随机响应分析。图7为振动频率在45.54 Hz时后封头处位移云图，可以看出，后封头底端粘接界面位移较大。在y轴方向上取4个参考点研究位移和应力情况，图8a为4点位移均方根值随频率的变化情况，图8b为4点加速度均方根值随频率的变化情况。可以看出，位移和加速度突变的频率在33 Hz附近。

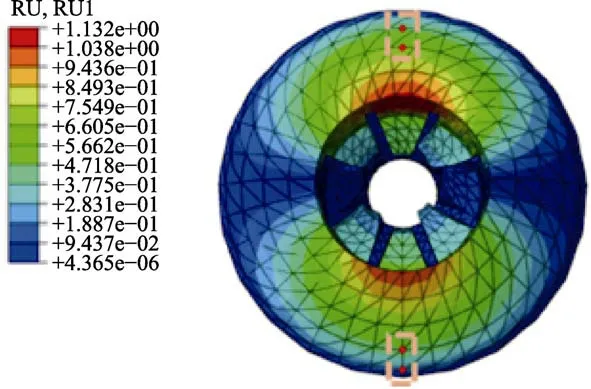
图7 位移云图 Fig.7 Displacement cloud

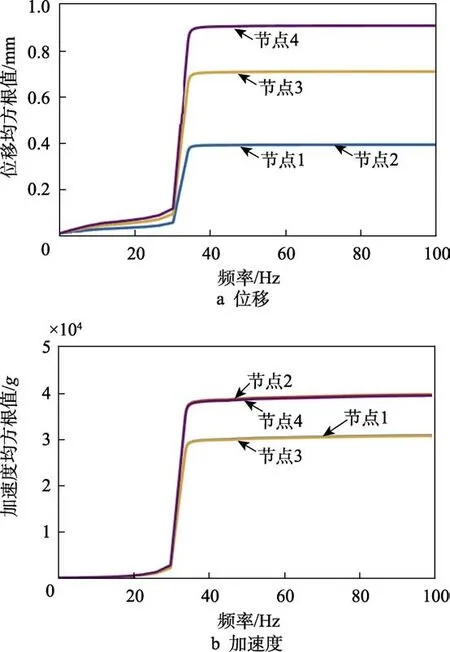
图8 频域中位移和加速度的均方根值 Fig.8 The RMS value of (a) displacement and (b) acceleration in the frequency domain

表4 模型各阶模态频率 Tab.4 Model frequency

2.3 发动机振动过程模拟

对于发动机粘接界面处所受应力情况，还需要将加速度数据作为载荷进行输入，模拟实际振动过程。振动开始时刻，假设发动机位移为0，将两种等级下加速度数据各提取300 s作为输入，施加在发动机模型外表面上，分析步间隔设置为0.1 s。图9显示了某一振动时刻下粘接界面处所受载荷情况。其中图9a为界面所受y22方向应力情况，可以看出，前封头及筒段处粘接界面所受应力较为均匀，约为25 kPa。在封头和圆筒段相接处应力值较大，特别是在后封头顶端，存在应力集中，应力值最大可达130 kPa。图9b为界面所受剪应力情况，可以看出，前、后封头处剪应力较小，圆筒段特别是靠近后封头处，剪应力较大，

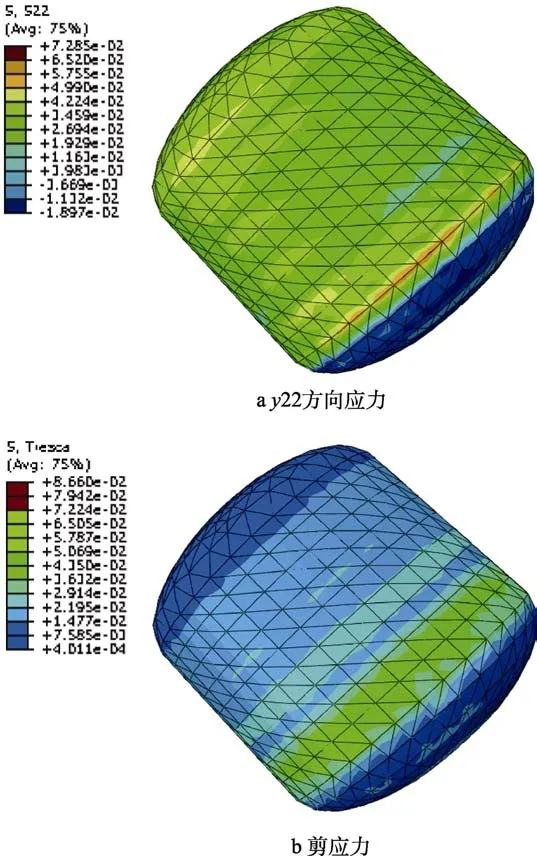
图9 粘接界面处所受载荷情况 Fig.9 Load condition of bonding interface: a) y22 stress; b) shear stress

剪应力整体要小于正应力。为对比不同振级下界面受载情况，提取筒段与后封头连接处正应力最大值点的应力历程，如图10所示。整体来看，B级振动载荷在界面上产生的应力远大于A级。从应力历程上看，每次出现较大冲击时，应力变化幅值会突然增大，然后迅速减小。主要是由于冲击初期壳体剧烈运动使得界面处药柱产生较大弹性变形，而后药柱迅速产生松弛效应，从而应力幅值迅速变小。

图10 应力历程 Fig.10 Stress history

3 结论

1）通过传感器实测获得导弹公路运输加速度数据，统计分析发现，信号属于超高斯分布，相关统计特征量表明，采集信号中包含冲击信号。以信号PSD值对载荷进行两级划分，求取等效PSD。

2）利用有限元软件Abaqus构建发动机模型，输入加速度PSD对发动机进行模态分析。结果表明，后封头底端粘接界面处位移较大，通过选取的4个参考点上看，位移和加速度均方根值突变的频率在33 Hz附近。

3）将加速度数据作为载荷进行输入，模拟实际振动过程发现，前封头及筒段处粘接界面所受应力较为均匀，在封头和圆筒段相接处应力值较大，特别是在后封头顶端存在应力集中。从应力历程上看，药柱的松弛效应使得冲击过后应力变化幅值迅速变小。同时应力历程数据可为后续试验提供基础。