时变分布式单位线在南方典型流域洪水模拟中的应用研究

王雅莉,梅国栋,王 莎,崔益源

矿冶科技集团有限公司,北京 102628

流域分布式水文模型发展至今，已取得了较大进步。由于其能够反映流域水文响应过程的空间异质性，水文模拟精度比集总式水文模型有明显的优势[1,2]。汇流是重要的水文过程之一，如何对流域进行概化，从而反映流域的汇流特性，是分布式水文模型关注的重点和难点[3]。

单位线是流域汇流计算的重要方法，可将流域对降雨的水文响应表示为降雨过程中一系列不同雨强输入的脉冲之和，地貌瞬时单位线和分布式单位线是其中的代表[4,5]。地貌瞬时单位线[6]建立了瞬时单位线参数与地貌参数的关系，因而能广泛应用于复杂地形地貌的流域汇流计算。Maidment[7]于1996 年提出分布式单位线，能够综合反应流域地形地貌和汇流路径空间分布，较地貌瞬时单位线又进一步，其关键是以DEM 为基础，计算流域各点降雨到达流域出口的汇流时间，构建流域汇流时间-面积关系，在我国部分地区已取得良好的模拟效果[8]。但传统的分布式单位线是把汇流当作时不变系统计算而来，与降雨过程等随时间变化的因素无关，这与流域系统的强非线性特征不符[9]。为此，本研究提出一种时变分布式单位线，综合考虑了雨强对汇流的影响，并基于中国山洪水文模型CNFF-HM 的框架，对比了时不变分布式单位线与时变分布式单位线支持下的流域洪水模拟结果。

1 模型与方法

1.1 分布式单位线

分布式单位线是在获得DEM 栅格汇流速度的基础上提取的，假设了落在栅格上的降雨是通过单一且连续的汇流路径到达流域出口，体现了将单位线的计算转化成了汇流时间计算的理念。美国农业部水土保持局国家工程手册中定义了坡面流域的计算公式[10]：

式中，V为栅格内的水流速度，m/s；S为沿水流方向的坡度；k为流速系数，m/s，主要反映了流速对土地利用特征等的响应程度。因此，根据栅格尺寸及水流速度，可计算得到水流在每个栅格中的滞留时间：

式中，Δτ为栅格内滞留时间，h；L为栅格边长，m。沿着汇流路径，求和流经的每个栅格的滞留时间，即为净雨到达流域出口的汇流时间。进而统计流域内所有网格汇流时间，得到其概率密度分布，即瞬时单位线，再利用下式将瞬时单位线转换为时段单位线[11]：

式中，Δt为时段；q(Δt,t)为时段单位线；F为流域面积，km2；S(t)为由瞬时单位线得到的S曲线。此单位线可称为时不变分布式单位线。

1.2 时变分布式单位线

早在1937 年，前苏联杜德金通过实验观测得到坡面流速计算公式[12]：

式中μ为参数；q为单宽流量，m2/s；S为坡度，表明坡面流域与单宽流量相关，而单宽流量可看作时段雨量与栅格边长的乘积。当栅格边长一定时，则反映出雨强与流速有很强的相关性。

综合已有研究成果以及式（1），提出时变分布式单位线坡面流速的计算公式：

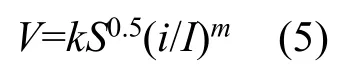
式中：k为流速系数，m/s；i为净雨强，mm/h，I为临界净雨强，mm/h。m取小于1 的正数。与式（2）相比，增加了(i/I)m项来综合考虑雨强对流速的影响，且流速与雨强呈正相关，当i＜I时增加较快，当i＞I时增加较慢，当i=I时式（5）变为式（2）。其中，m可取0.4，I取40 mm/h。图1 展示了同一流域不同雨强下栅格的汇流时间分布，证明了雨强是影响汇流时间的关键要素。

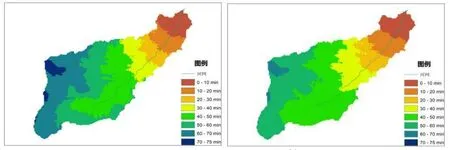
图1 不同雨强下栅格汇流时间Fig.1 Grid flow concentration time with different rain intensity

1.3 CNFF-HM 与参数

为了对比时不变分布式单位线与时变分布式单位线的洪水模拟结果，研究选用了中国山洪水文模型CNFF-HM 框架[13]，只更改其坡面汇流模块，产流、河道演进等模块保持一致。其中，蒸散发采用三层蒸散发模型，产流采用三水源新安江产流模型，壤中流和地下水汇流采用线性水库、河道汇流采用动态马斯京根法。CNFF-HM 模型主要参数如表1 所示，模型参数率定选用遗传算法与人工相结合的方法[14]。

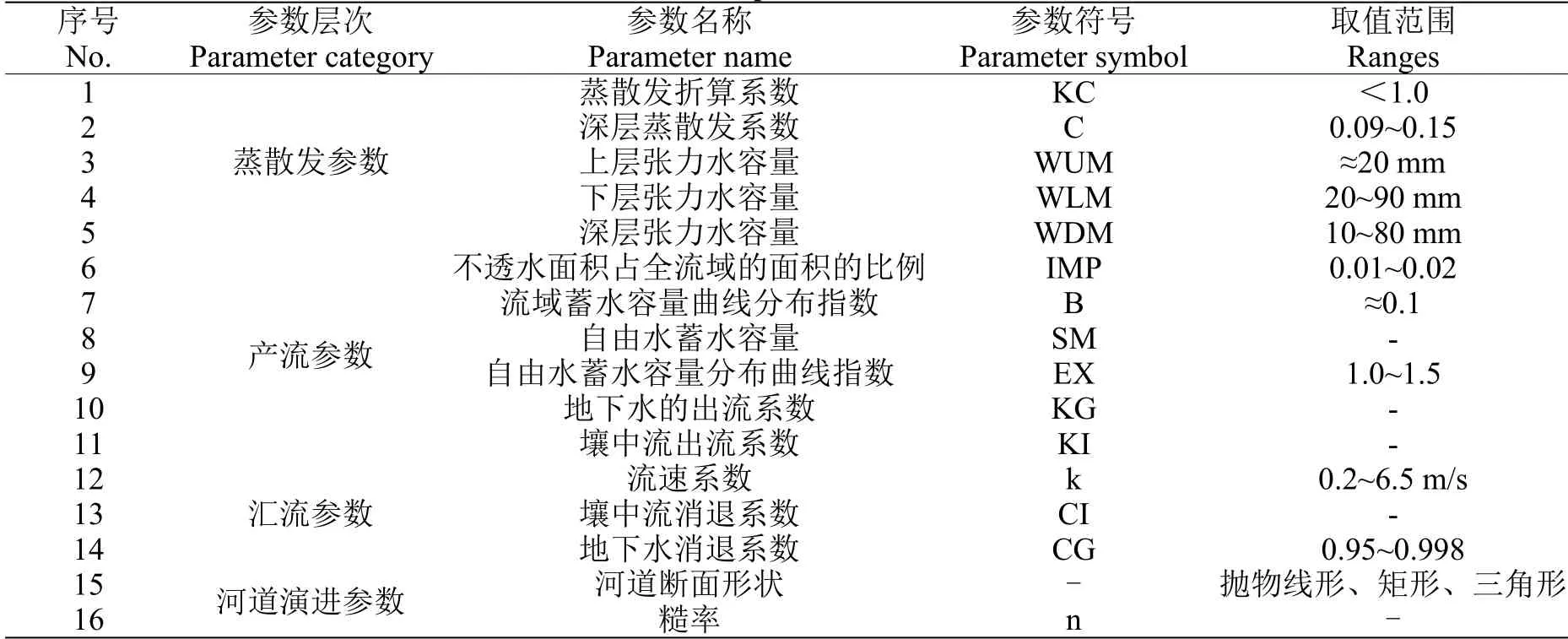
表1 CNFF-HM 主要模型参数Table 1 Main model parameters in CNFF-HM

2 研究区与资料

选择我国湿润地区数据较完整、资料条件较好的8 个流域（见图2）。选取流域的年均降雨量为1000 mm～2000 mm，属于我国降雨量大、暴雨频发的地区。流域以中小流域为主，面积为79～1095 km2。基于国家地理信息中心提供的DEM，划分CNFF-HM 的基本计算单元（子流域），再基于国家地理信息中心提供的DOM，在基本计算单元的基础上，结合水文站和水利工程等，将子流域合并为流域（见表2）。

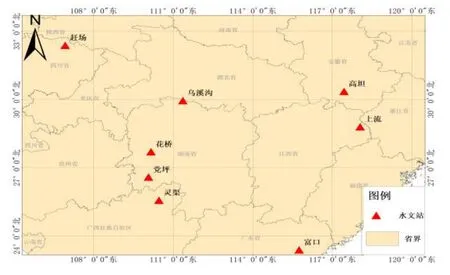
图2 流域位置图Fig.2 The location of eight catchments

表2 流域概况Table 2 General situation of the catchments

各流域土地利用及植被覆盖数据是通过人工判读、机器解译、人机交互解译、人工核查相结合的方法，在30 m 和优于（含）2.5 m 分辨率的DOM 等资料基础上，提取形成流域土地利用和植被类型数据[15]。各流域土壤类型与土壤质地资料来源于1:50 万土壤类型数据和全国1:100 万土壤剖面数据。8 个流域的水文站、雨量站以及洪水场次等信息见表3。流域的降雨径流资料来源于各省水文局及防汛部门。

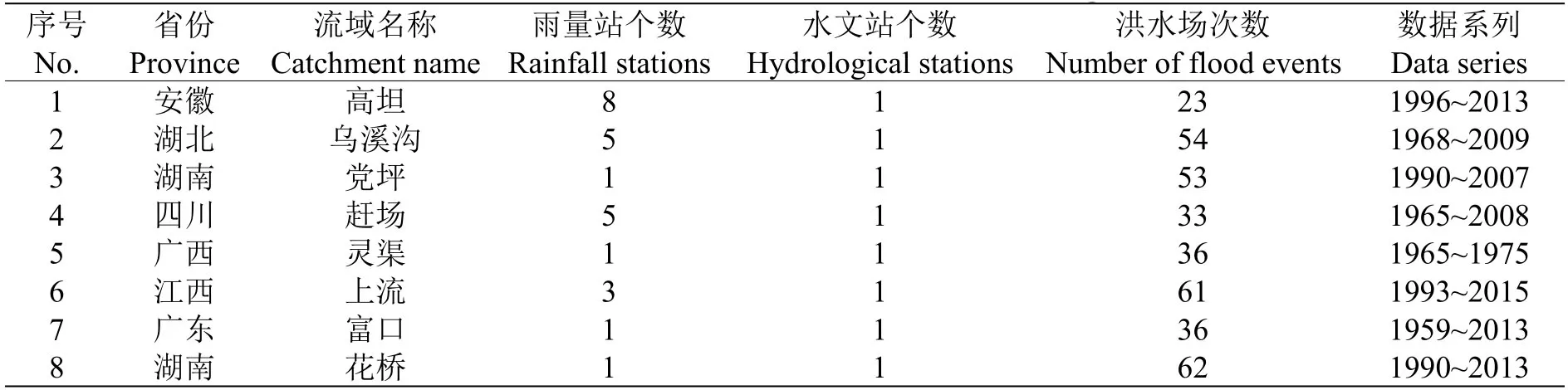
表3 流域内站点与降雨径流资料Table 3 Number of stations and rainfall-runoff data in the eight catchments

3 结果与分析

3.1 两种分布式单位线的模拟结果对比

以8 个流域收集到的降雨径流资料系列为基础，对时不变分布式单位线与时变分布式单位线的模拟结果进行评估对比。各流域降雨径流资料系列的前2/3 场次作为模型的率定期，后1/3 场次作为模型验证期。模型模拟结果评估按照《水文情报预报规范（GB/T 22482-2008）》中的洪峰流量误差RF、峰现时间误差△T和纳什效率系数NSE[16]。率定和验证的结果如表4 和5 所示。

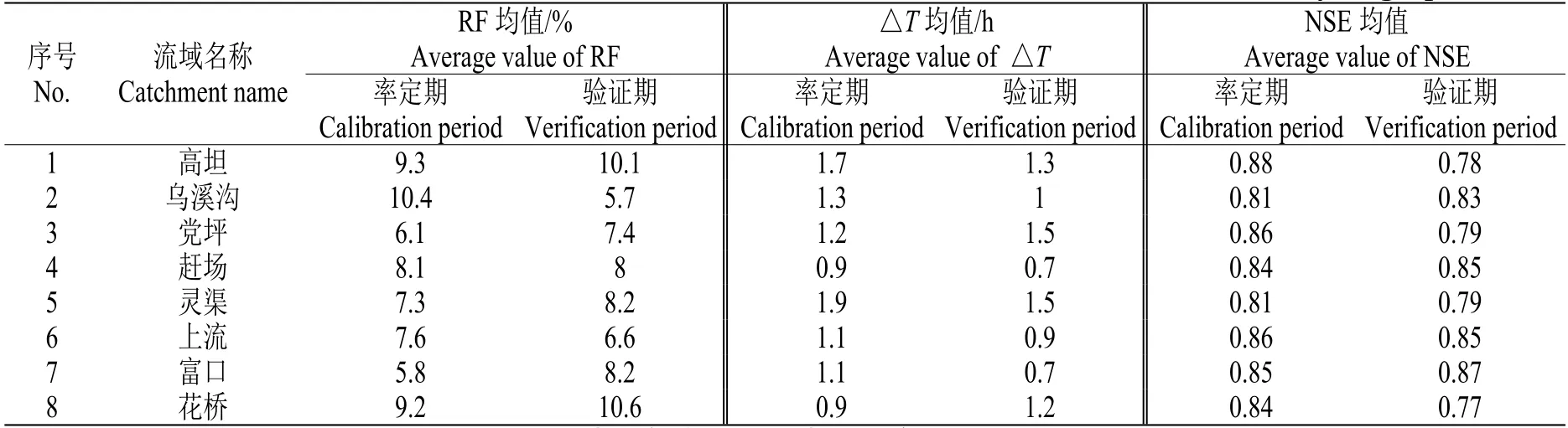
表4 时变单位线的模型率定和验证结果Table 4 Results for model calibration and verification with time-variant distributed unit hydrograph

表5 时不变单位线的模型率定和验证结果Table 5 Results for model calibration and verification with time-invariant distributed unit hydrograph

由表4 和5 表明，各流域时不变分布式单位线模拟的各流域率定期和验证期的RF 均值都小于20%，△T均值都小于2 h，但NSE 均值只有乌溪沟、赶场、上流三个流域率定期和验证期都在0.7以上，其他流域均低于0.7；时变分布式单位线模拟的各流域RF 均值都小于20%，△T均值都小于2 h，8 个流域率定期和验证期的NSE 均值都大于0.7，结果较好。为了进一步直观对比两种单位线的模拟结果，采用《水文情报预报规范（GB/T 22482-2008）》规定的合格率和等级进行再评估，结果表明8 个流域在率定期或验证期，时变分布式单位线比时不变分布式单位线的模拟结果合格率更高，评估等级高一级。

表6 两种分布式单位线合格率对比Table 6 Qualification rate comparison for two distributed unit hydrographs

3.2 两种分布式单位线的尺度效应

为了进一步探究两种分布式单位线在不同面积大小的流域的应用效果，计算两种分布式单位线的模拟效果差值随面积的变化趋势图（见图3）。由图3 可知，两种分布式单位线计算的RF、△T、NSE 三个指标的差值随流域面积的减小均呈现增加趋势。以NSE 为例，当流域面积小于100 km2时，两种分布式单位线模拟的差值达到0.12 以上，差异较大；当流域面积大于500 km2时，NSE 差值小于0.04，模拟效果更接近。两种分布式单位线模拟的RF、△T均可得到一致的结论。因此，流域面积增大使得两种分布式单位线的计算结果趋于吻合。

图3 两种单位线计算差值与面积关系Fig.3 Relationship between the catchment area and difference of two distributed unit hydrographs

时变分布式单位线与雨强相关，是根据每个子流域的降雨过程，按照时段降雨过程动态选择单位线进行计算。流域面积越大，划分子流域个数越多，而同时段不同子流域的降雨过程不同，因此其选择的汇流单位线也不同。流域面积越大，不同雨强下的子流域产生的流量被均化，雨强对分布式单位线的影响较小，两种分布式单位线的计算结果就越接近。

4 结论与讨论

本研究提出一种时变分布式单位线，综合考虑了雨强对汇流的影响，并基于中国山洪水文模型CNFF-HM 的框架，选择了我国湿润地区8 个典型流域，对比了时不变分布式单位线与时变分布式单位线支持下的流域洪水模拟结果，主要结论如下：

（1）提出的时变分布式单位线是在时不变分布式单位线的基础上，综合考虑了雨强对汇流时间的影响，为流域水文模型提供一种可靠的汇流计算方法，为流域洪水预报提供技术支撑；

（2）8 个典型流域的模拟结果表明，时变分布式单位线比时不变分布式单位线的应用效果更好，时不变分布式单位线得到的NSE 均值只有乌溪沟、赶场、上流三个流域率定期和验证期都在0.7 以上,而时变分布式单位线得到的NSE 均值都在0.7 以上，且时变分布式单位线比时不变分布式单位线的模拟结果合格率更高，评估等级高一级；

（3）随着流域面积的增大，受不同雨强下的子流域产生流量被均化的影响，时变分布式单位线的模拟结果更接近时不变分布式单位线，因此时变分布式单位线更适用于小流域的洪水模拟预报。