螺旋桨空泡脉动压力试验不确定度分析

孙 硕， 伍 锐， 刘 恒

(上海船舶运输科学研究所 a.航运技术与安全国家重点实验室；b.航运技术交通行业重点实验室， 上海 200135)

0 引 言

开展螺旋桨空泡脉动压力试验既是研究螺旋桨空泡振动性能的重要手段，也是船舶设计研究的一项重要内容。该试验通常在空泡水筒内进行,试验本身存在一定的误差，开展不确定度分析是对该误差进行分析并量化其范围的一种有效手段。为使试验结果更准确，需对试验仪器的使用、试验环境和试验数据分析方法等进行严格把控。国际拖曳水池会议(International Towing Tank Conference, ITTC)对空泡脉动压力试验流程有全面、详细的建议，对试验的不确定度分析有一定的指导意义。

周军伟等采用计算流体力学(Computational Fluid Dynamics，CFD)方法对螺旋桨空泡的形态和脉动压力的变化机理进行剖析，说明了桨叶表面空化与脉动压力之间的关系。张立等参考ITTC推荐规程，通过研究船模阻力试验，详细阐述了不确定度分析的原理和方法。伍锐等通过试验研究了空泡水筒内的空气含量、伴流场和模型转速对脉动压力的影响，结合德国汉堡水池空泡实验室的试验数据探究了脉动压力在不同影响因素下的变化规律。

目前,已有的船舶水动力不确定度研究主要集中在船舶阻力分析、螺旋桨试验不同影响因素对应的现象分析等方面，很少对螺旋桨空泡脉压试验的不确定度计算进行研究。本文主要根据ITTC规范，结合试验对试验仪器、试验环境和试验数据等参数的不确定度进行计算分析。

1 不确定度分析

1.1 不确定度分析原理

一种定义明确的物理量可用唯一的测量值表征，但测量结果的真实性存在不确定性，不能完全代表被测物理量的值。计量指南联合委员会将不确定度归纳为标准不确定度、合成不确定度和扩展不确定度等3种，其中标准不确定度又分为A类不确定度和B类不确定度。

被测物理量

Y

一般不是直接测得的，而是先通过试验测得

X

、

X

、…、

X

等其他物理量，再通过相应的函数关系

f

求得。这种测量方程可归纳为

Y

=

f

(

X

,

X

,

X

,…,

X

)

(1)

函数关系

f

不仅表示物理定律，而且表示测量过程，尤其是所有可能影响被测物理量

Y

的不确定度的量。不同的变量因传递函数不同而具有不同的敏感度。在数据点附近进行泰勒展开，便可近似得到

X

处的误差δ

r

，d

r/

d

X

即为该处的灵敏度系数。图1为不确定度的传递路径；图2为传递函数示意。

图1 不确定度的传递路径

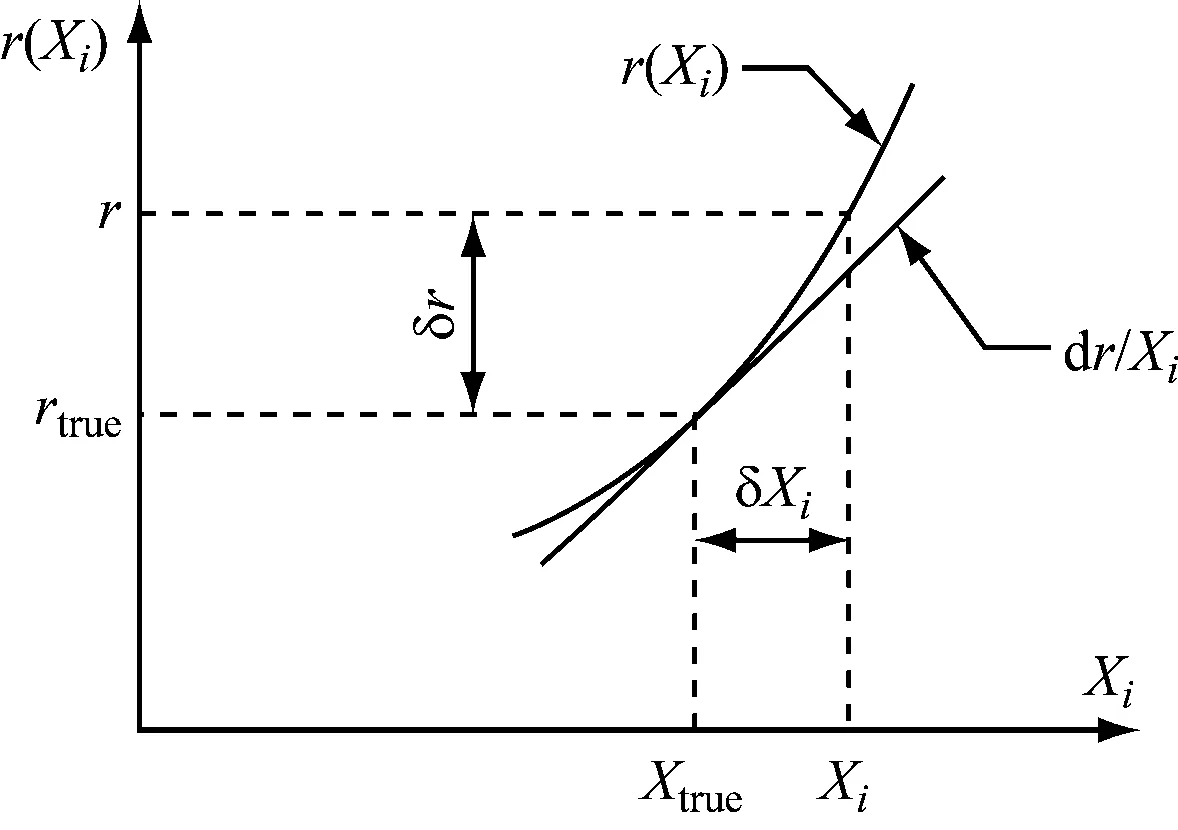
图2 传递函数示意

合成不确定度由不确定误差传递定律确定，对A类不确定度和B类不确定度进行计算，即可得到不确定度

u

。

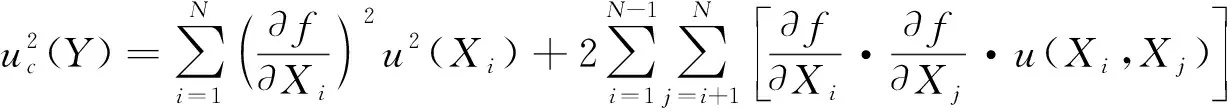
(2)

式(2)中：

N

为测量总次数；∂

f/

∂

X

和∂

f/

∂

X

分别为变量

X

和

X

的灵敏度系数；

u

(

X

)和

u

(

X

)分别为变量

X

和

X

的不确定度。当

X

和

X

属于不相关变量时，式(2)可表示为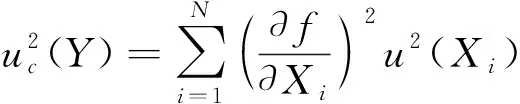

(3)

式(3)为不确定度传导最常用的形式。

水动力学中相对不确定度的测量方程为

Y

=

cX

1,·

X

2,·…·

X

,

(4)

将式(4)代入公式(3)，可得相对不确定度的表达式为

(5)

1.2 脉动压力试验流程

脉动压力试验中的不确定度由很多因素构成，在计算不确定度时，需明确试验流程和误差来源。脉动压力试验误差来源主要包括螺旋桨模型误差、伴流场误差、水环境误差、安装误差、设备仪器误差和测量结果误差等(见图3)。

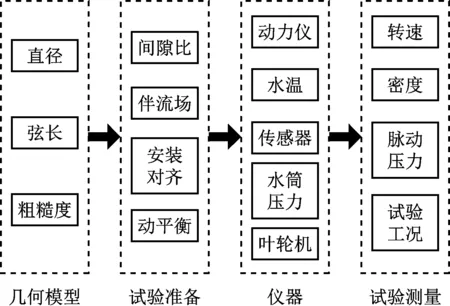
图3 脉动压力试验误差来源

1.3 脉动压力不确定度分析方法

根据上述不确度分析方法，结合脉动压力计算公式进行分析，有

K

=

P

·

ρ

n

D

(6)

式(6)中：

K

为第

i

阶叶频谐波分量脉动压力系数；

P

为第

i

阶叶频谐波分量的单幅值；

ρ

为水的密度；

n

为螺旋桨的转速；

D

为螺旋桨的直径。1

.

3

.

1 螺旋桨模型的不确定度由式(6)可知，螺旋桨的直径

D

对试验结果有影响。

D

的相对不确定度的表达式为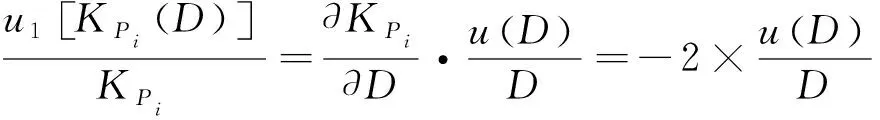

(7)

式(7)中:

u

(

i

=1,2,…,

N

)为被测参数的不确定度。1

.

3

.

2 设备和环境的不确定度

设备和环境的不确定度主要包括J25动力仪的转速误差、密度和传感器本身的误差等。

1) 通过对式(6)进行分析可知，动力仪的转速

n

(即螺旋桨的转速)对试验结果有影响，即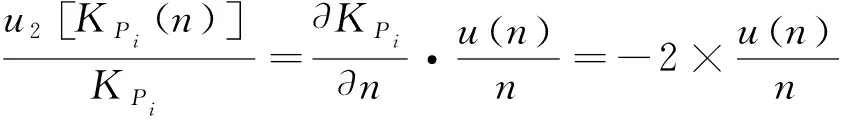

(8)

2) 水温发生变化引起密度

ρ

发生变化，进而影响试验结果，即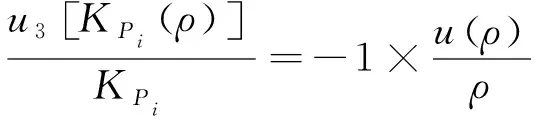

(9)

3) 脉动压力传感器会直接对试验结果产生影响，其不确定度可直接计入总体不确定度，即

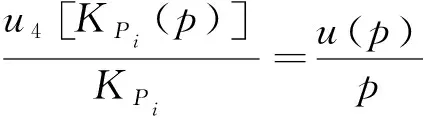
(10)

式(10)中：

p

为脉动压力传感器。1

.

3

.

3 试验数据的不确定度

在对不确定度进行试验研究时，一般进行多次重复试验，得到丰富的试验数据，其平均值和相对不确定度可表示为

(11)

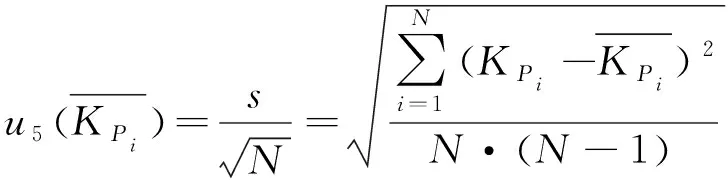
(12)

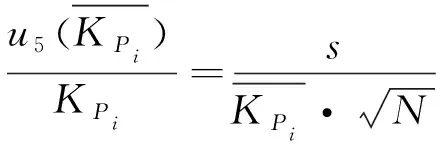
(13)

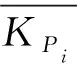
1.4 合成标准不确定度和扩展不确定度

在上述分析的基础上，通过对各分项的相对不确定度进行合并，可得到试验结果的相对不确定度，有

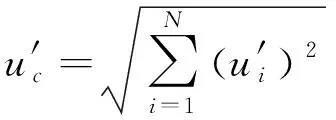
(14)

(15)

2 脉动压力试验和不确定度分析

在上海船舶运输科学研究所空泡水筒内进行螺旋桨空泡脉动压力试验，共有常压、设计吃水、压载吃水等3种工况，对每种工况采集10组数据进行分析。螺旋桨参数和试验工况见表1;脉动压力试验设备安装示意见图4。

表1 螺旋桨参数和试验工况

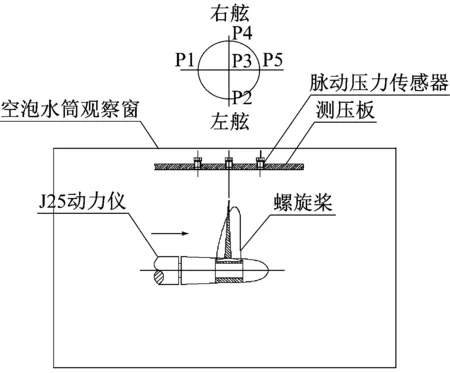
图4 脉动压力试验设备安装示意

2.1 测量仪器的不确定度

为明确各误差源对脉动压力的影响，首先对测量仪器的B类不确定度进行计算。

2.1.1 螺旋桨模型

试验前通过肉眼检查螺旋桨模型的缺口、局部损伤和伤后修补情况。模型加工偏差应在规定的加工偏差内。试验时尽量保证螺旋桨模型在试验工况下不变形。导边和叶梢边缘有更高的精度要求。对螺旋桨模型实际加工尺寸进行统计可知，其最大偏差为240 mm±1 mm，因此螺旋桨直径的相对不确定度为0.42%。

2.1.2 螺旋桨转速

由J25动力仪的设备精度可知，螺旋桨转速的不确定度为0.20%。

2.1.3 水温和密度

试验在同一天的较短时间内完成，密度变化对试验结果的影响较小，产生的误差主要为温度计水温读数误差，根据试验经验，0.5 K的误差对应密度的不确定度为0.015%。

2.1.4 脉动压力传感器

5台脉动压力传感器均位于螺旋桨正上方，各脉动压力传感器之间的距离控制在0

.

15

D

～0

.

35

D

范围内，此次试验中各脉动压力传感器之间的距离为50 mm，脉动压力传感器的不确定度为0.20%。

2.2 试验数据的不确定度

对在3种工况下采集的螺旋桨脉动压力数据进行不确定度分析，结果见表2和图5。由图5a可知，同一工况下传感器不同位置之间的脉动压力值的不确定度差异不大，低阶时基本相同。由图5b可知，3种工况下脉动压力值在低阶时的不确定度较小，可信度较高，在高阶时的不确定度有增大的趋势。在常压工况下，脉动压力值在高阶时具有较大的不确定度，但其量级很小，在此不予讨论。

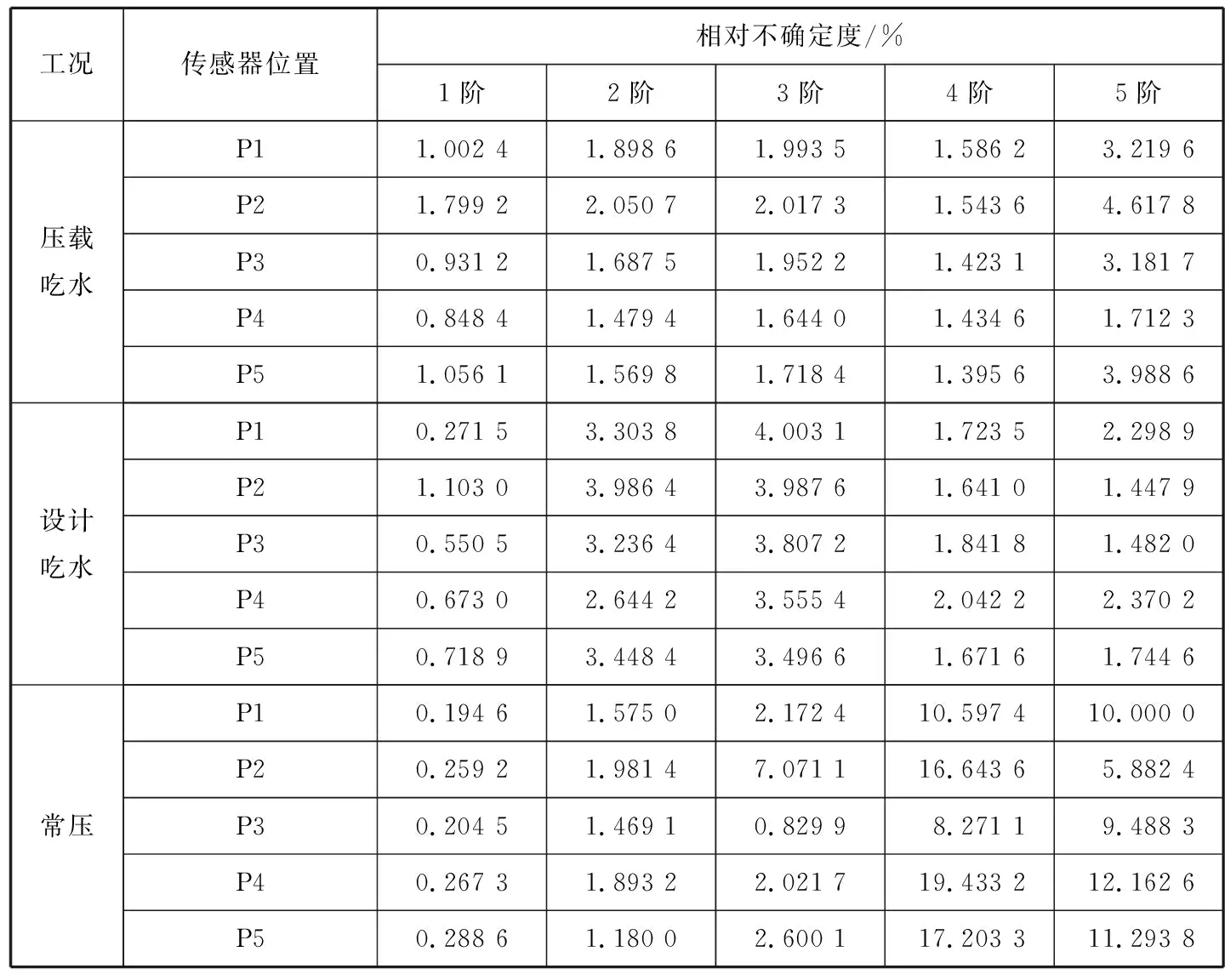
表2 试验数据相对不确定度

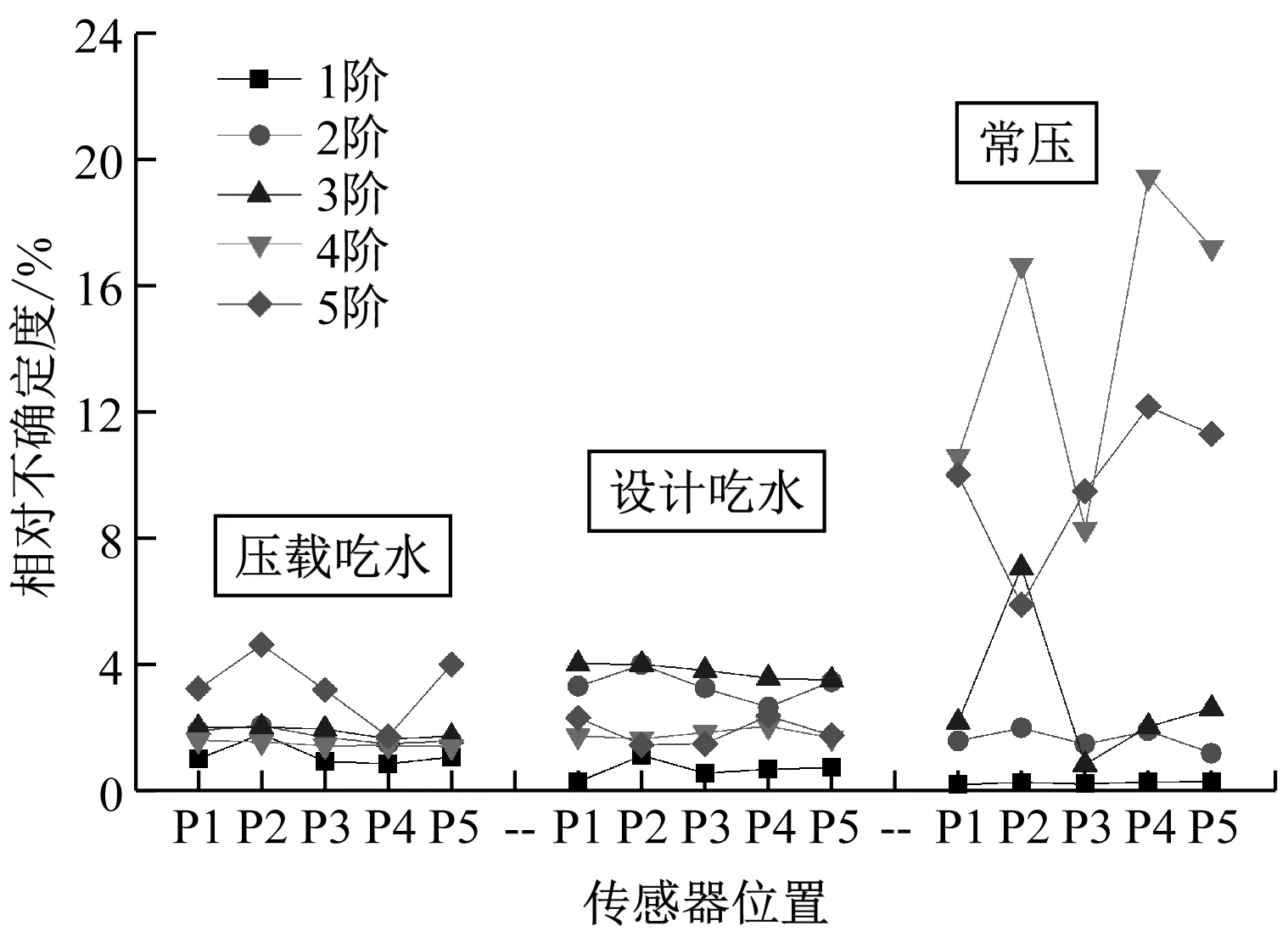
a) 不同传感器位置的相对不确定度

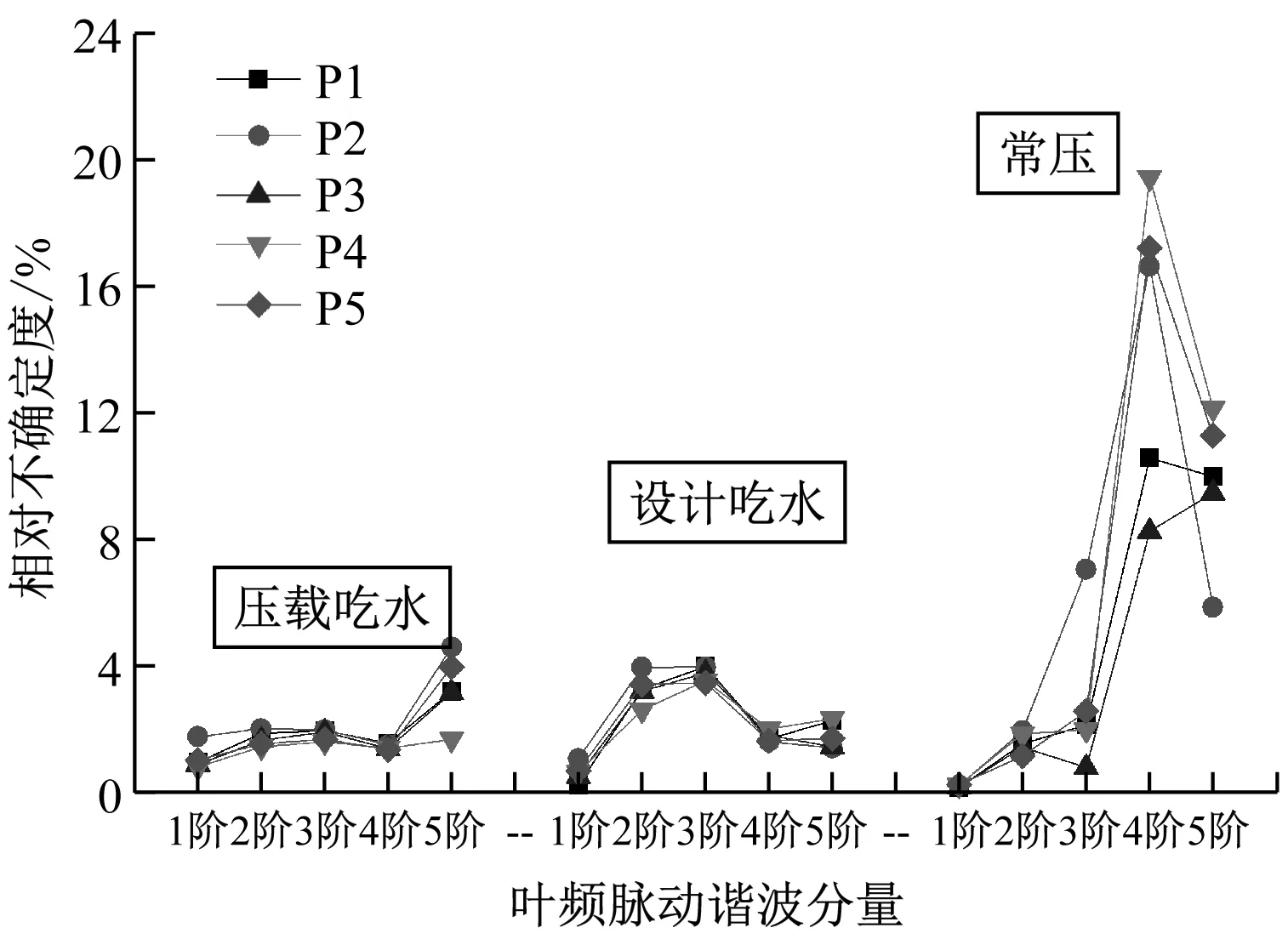
b) 不同叶频脉动谐波分量的相对不确定度图5 试验数据相对不确定度

3 合成不确定度和扩展不确定度

分别选取3种工况下的最大1阶脉动压力幅值，并将其相对不确定度与B类不确定度合并，可得脉动压力试验的不确定度。

在工程试验不确定度评定中，灵敏度系数

c

可理解为每个变量的不确定度对最终试验结果不确定度的影响，可直接根据式(7)～式(10)求得；将测量仪器和试验数据不确定度代入式(7)～式(11)，可得各参数对脉动压力试验结果的影响。表3为各参数对脉动压力试验结果的影响；表4为脉动压力系数

K

的不确定度分析结果。从表3和表4中可看出：B类不确定度中螺旋桨直径对脉动压力试验结果的影响最大，螺旋桨转速对脉动压力试验结果的影响次之，说明脉动压力试验对模型和设备有较高的精度要求；水的密度对脉动压力试验结果的影响较小；在3种工况中，随着转速空化数的减小，各参数的相对不确定度增加，说明工况的变化对试验结果的影响较大，工况越恶劣，试验结果的相对不确定度越大。由式(6)可求出不同工况下的脉动压力系数，脉动压力系数与试验结果一一对应。图6为3种工况下各参数的相对不确定度。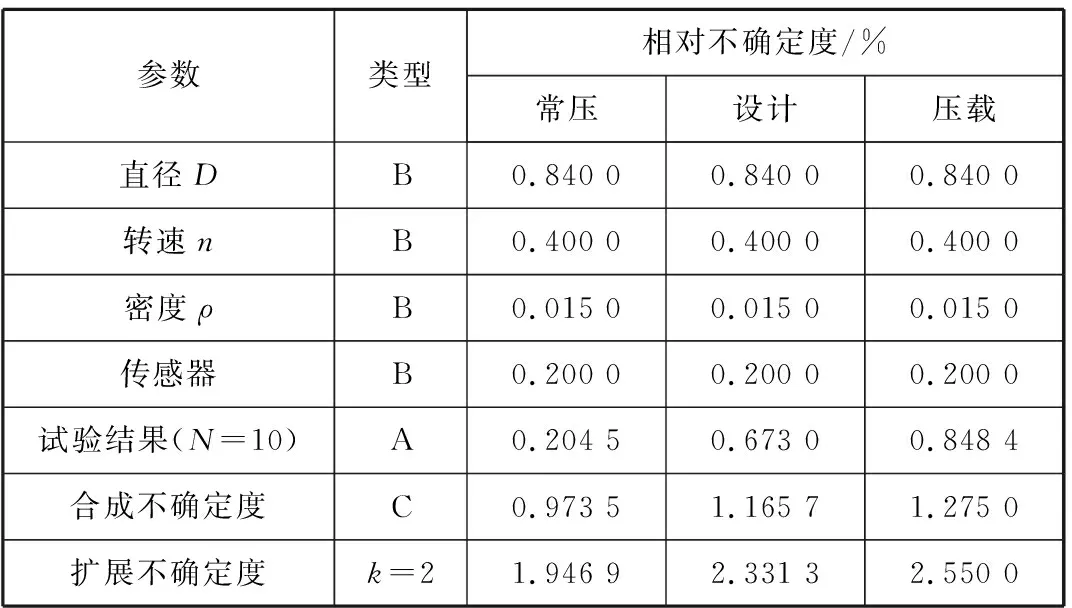

表3 各参数对脉动压力试验结果的影响

表4 脉动压力系数KPi的不确定度分析结果

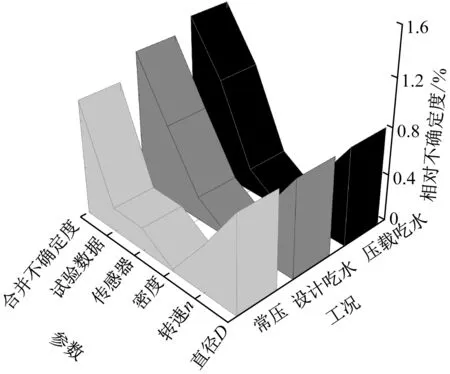
图6 3种工况下各参数的相对不确定度

4 结 语

本文依照ITTC推荐的相关规程，对螺旋桨空泡脉动压力试验的不确定度进行了分析，针对3种工况分别进行了10次数据采集。通过分析试验流程，明确了试验误差的来源，并根据其类型和规范对试验的不确定度进行了计算。通过对脉动压力计算公式进行泰勒展开，得到了不确定度源的灵敏度系数；按照公式对标准不确定度进行合并，得到了脉动压力试验结果的不确定度。通过上述研究，主要得到以下结论：

1) 脉动压力结果的扩展不确定度在95%置信水平(

k

=2)下，相对不确定度均在3%以内。

2) A类不确定度中,试验数据最大1阶脉动压力值的不确定度在1%以内;B类不确定度中,螺旋桨直径对试验结果的影响最大，转速和传感器对试验结果的影响次之，密度对试验结果的影响相对较小。

3) 工况越恶劣，脉动压力系数的不确定度越大，因此在恶劣工况下，需更加注意对细节的把握，以减小系统误差和随机误差。

需指出的是，此次试验仅对脉动压力试验常规的不确定度进行了量化计算，初步了解了各参数对试验结果不确定度的影响。脉动压力试验的影响因素众多，如伴流场、间隙比等对脉动压力测量也有很大影响，后续将继续开展对这些因素的研究，进一步完善螺旋桨脉动压力试验不确定度分析方法。