基于执行者过程树的双维度遗传过程挖掘方法
汤雅惠,李 彤,朱 锐,南峰涛,付会林
(1.云南大学 信息学院,云南 昆明 650500;2.云南大学 软件学院,云南 昆明 650091;3.云南农业大学 大数据学院,云南 昆明 650201)
0 引言
过程挖掘能从现代信息系统中提取有价值的过程知识,起到对过程进行发现和监督,最终达到过程改进的作用。过程挖掘是管理复杂运作过程的一种有效的工具,其目标是能够快速生成一个高简洁度、高拟合度、高精确度以及高泛化度的过程模型,最终指导过程的分析和改进[1]。
现今,过程挖掘方法仍处于不断发展和革新中。应用于控制流维度的挖掘算法[1]也非常多,不同算法的适用范围各不相同,故而其对应的优点和缺点也不同。例如遗传挖掘(Genetic Process Mining, GPM)算法[2]将4个质量维度作为模型挖掘导向,使其得到的模型较其他算法质量更高。但由于GPM算法使用迭代的方法模仿生物自然演变,当处理数据量较为庞大和结构复杂的事件日志时,种群的准备时间和算法的迭代时间将成倍增长,进而大大降低算法的效率。
事件日志还包含与过程相关的人员组织的大量信息,这些信息同样蕴含价值。组织维度[3]的关注点在于组织中人与人之间的关系。对组织维度进行挖掘可以发现典型的组织结构和社交网络(social net)[4]。社交网络模型可以学习关于人、组织结构(角色和部门)和工作分配的知识。组织知识的发现使管理人员能够了解组织结构,进而改善组织运作过程。例如,社交网络可以显示企业中的沟通结构,这可用于设计通信基础结构或办公室布局。
对于业务过程而言,过程的发生与变化,源自于人,而过程模型的发现与改进,最终还是服务于人。因此,与组织维度相关的人的行为与交互,对于业务过程的影响举足轻重。同时,现代工业产品是人类脑力和体力结合的产物。随着企业规模的增长和产品开发技术的进步,企业的分工和组织也变得越来越复杂。有效地组织和划分人员的方法是使企业价值最大化的决定性因素。因此,发现和分析过程中涉及的组织维度信息至关重要。而与在控制流方面的研究相比,目前在组织维度方面的研究还比较少[5-6]。
控制流维度模型反映活动之间的关系,组织维度模型反映组织人员之间的关系。两个维度属于不同层面。而在人类扮演主要角色的环境中,过程的运行与人类行为高度相关,人的行为与决策对活动的影响至关重要。例如,在软件开发组织、医院等许多其他专业组织中,过程的出现和变化多是由于人为决策。因此,将两种维度分割来看,较难获得全局视角,不能直观看出人员在不同活动上的分工,难以对事件日志进行全面的分析。而如果能够在同一个模型中同时展示两种维度,反映人与活动之间的关系,则能获得更为全面的视角。目前,关于组合两种维度的研究较为罕见,文献[4]将日志中的事件与其所对应的模型中的元素连接起来,通过仿真工具基于该映射将多个维度合并。然而,在一个事件日志和模型之间建立一个好的连接较为困难。本文将两种维度组合,以执行者过程树的形式,在同一个模型中同时反映两个维度的信息,能有效体现出活动与执行者之间的关系。以此提供一种新的洞察力,有助于更准确地对过程进行分析。具体地,本文在控制流维度方面,针对遗传挖掘算法的不足进行改进,目的是生成高质量的控制流模型;然后使用组织维度扩展模型,度量活动在执行者层面的距离,并为控制流模型添加执行者信息。
本文的主要贡献如下:
(1)在控制流维度,提出遗传过程混成挖掘算法。在预处理阶段,使用归纳挖掘算法(Inductive Miner, IM)[7]处理事件日志,以为遗传过程挖掘算法提供质量较高的初始过程树种群,从而简化它的挖掘环境、提高算法效率。同时,定义综合质量函数,使算法有效平衡4个质量维度。
(2)在组织维度,基于活动—执行者矩阵,提出活动相似度度量方法,能有效度量活动在执行者层面的相似度,进而获得组织结构(角色和部门)和工作分配的信息。
(3)使用组织维度扩展控制流模型,基于执行者过程树,建立双维度过程模型。
1 国内外研究现状及发展趋势分析
控制流发现算法旨在发现活动之间的控制流关系。目前,已经提出许多发现算法[1],它们各有各的适用范围以及优缺点。但是这些方法很难在算法效率以及模型的4个质量维度(包括精确度(Precision)、简洁度(Simplicity)、泛化度(Generalization)以及拟合度(Fitness))方面取得平衡。目前,相关研究表明,α算法[8]生成的过程模型不能确保简洁性,且其不能处理短循环结构,不能考虑发生次数。启发式挖掘[9]将低频事件视为噪声,故其生成的模型的拟合度相对较差[10]。基于区域的挖掘算法[11]可以处理具有复杂结构的事件日志,且能生成具有较高精确度的过程模型,但可能导致空间爆炸,同时算法效率不高。
遗传挖掘算法源于遗传算法,由DE MEDEIROS等[2]提出。最初使用因果矩阵对算法内部的模型进行表示,但该方法将导致模型存在死锁。为解决该问题,AALST等[12]提出并使用过程树作为遗传挖掘算法内部过程模型的表示形式,虽然可以解决死锁问题,但在处理大型事件日志时依然存在问题——算法的效率和挖掘所得模型的质量难以达到较好的平衡,即如要挖掘生成较高质量的过程模型,必须以大量的时间做支撑。而本文所提方法通过预挖掘,可以有效提高遗传挖掘算法初始种群质量,减少算法挖掘生成更高质量模型所需要的迭代次数,最终加快其收敛速度。
组织挖掘的起点始于事件日志中存在的资源属性,即该活动是由哪位执行者完成的。SONG等[4]对组织挖掘方法进行了详尽的描述。对组织维度的挖掘分析方法主要分为3种:①组织维度模型(主要是社交网络)挖掘;②社交网络分析;③组织实体之间的信息流分析。组织模型挖掘可以对具有相似特征的执行者进行分组,相似特征判断既可以基于活动相似性,也可以基于案例相似性;社交网络分析的主要目的是探索活动如何在不同的执行者之间处理和传递,它展示了执行者之间的关系,由代表执行者的实体和代表关系的弧组成,弧带有权重,权重代表执行者之间的距离,距离则通过计算两个执行者在相同案例上工作的次数来度量[4];组织实体之间的信息流分析,主要指对社交网络中收集的信息进行汇总,以产生组织实体(例如角色或组织单位),这些实体可提供更高抽象级别的见解。组织实体的构建考虑了度量标准以及派生的社交网络和聚合节点,可以根据原始网络的权重对这些新连接进行加权。目前组织维度挖掘主要基于对社交网络的分析,而本文通过活动—执行者矩阵在执行者层面上度量活动之间的距离,活动越近,则该活动的执行者越相似,从而反映该事件日志的组织结构特征。
2 控制流与组织维的双维度遗传过程挖掘方法
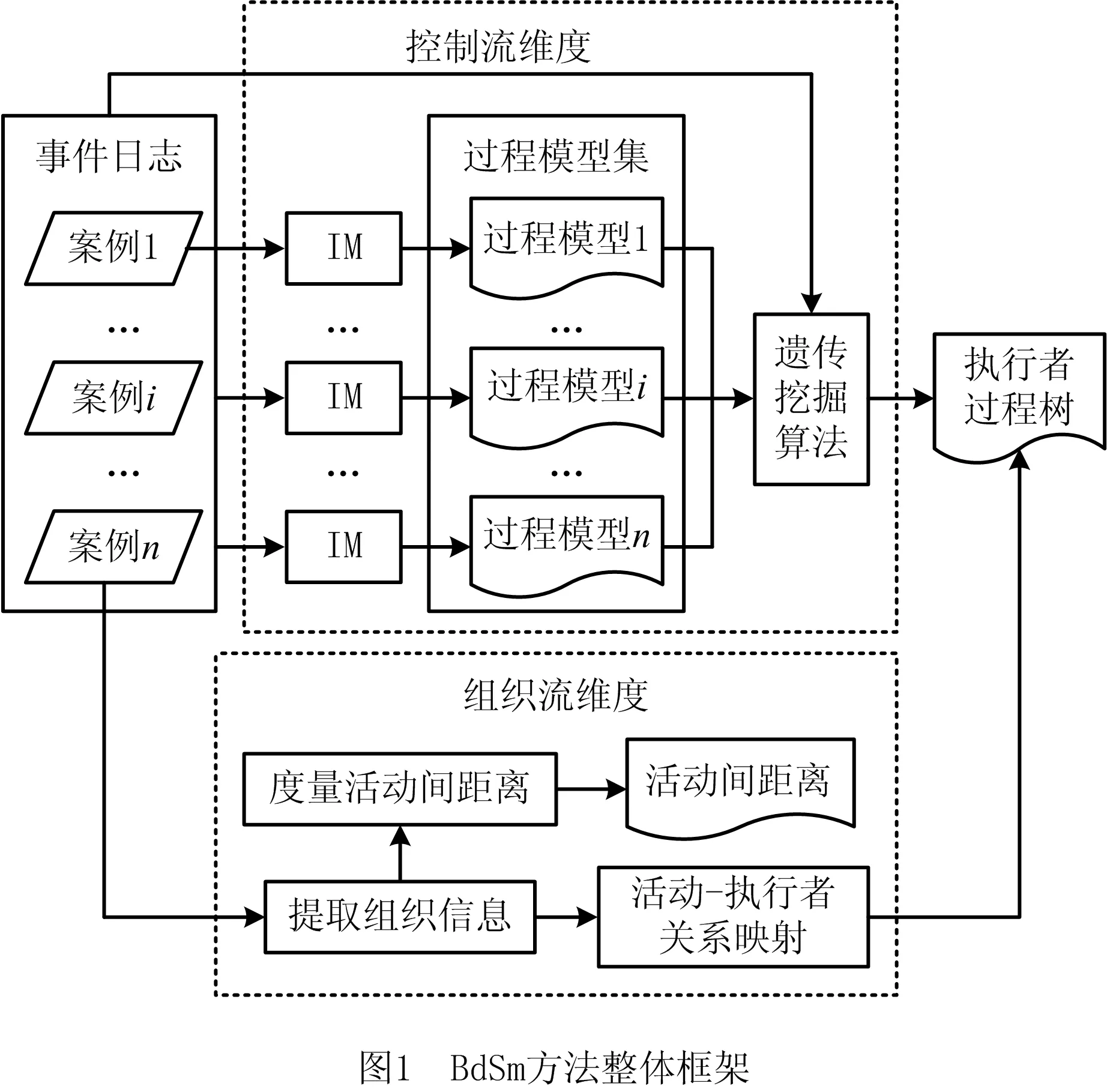
本文提出的双维度遗传过程挖掘方法(double-dimenSional genetic process mining method based on excutor process tree, BdSm)如图1所示。将事件日志作为方法的输入,得到的双维度过程模型作为方法的结果输出。BdSm方法由两个维度构成:①控制流维度,使用IM算法分别对案例进行挖掘,并将其得到的过程模型作为GPM算法的初始种群,进一步通过GPM算法对其进行整合优化,最终得到与日志相对应的过程模型;②组织维度,提取组织信息,用于拓展过程模型。具体的,一方面通过活动—执行者矩阵度量活动在执行者层面的距离,另一方面将活动与其对应的执行者建立映射,得到执行者过程树。目前该方法已在过程挖掘工具ProM[13]中进行实现。下面将分别对方法进行说明,首先介绍相关定义。
定义1事件,事件属性[8]。令ε为所有可能事件标识符的集合,即事件空间,事件具有多个事件属性,如:事件的执行者的名称、执行事件所需成本以及事件的时间戳等。其中:
(1)属性名集合为N;
(2)对于∀e∈ε及属性名称n∈N,将事件e的属性n所对应的值记为#n(e);
(3)若n属性不属于事件e,则#n(e)=⊥。
为方便起见,定义以下标准属性:
#activity(e)为事件e相关联的活动,将某个事件上的活动集合简记为A;
#resource(e)为事件e相关联的执行者,将某个事件上的执行者集合简记为R;
对于事件e=(a,r),设a∈A,r∈R,定义πa(e)=a,以及πr(e)=r。(a,r)表示活动a由执行者r执行。
定义2案例,轨迹,事件日志[8]。令C为所有可能的案例标识符的集合,即案例空间,案例也具有多个案例属性。
(1)对于∀c∈C和属性名称n∈N,#n(c)为属于案例c的属性n对应的值。
(2)若n的属性不属于案例c,则#n(c)=⊥。
(3)强制属性——轨迹,是每个案例所必须具有的:即#trace(c)∈C*,将轨迹简称记为=trace(c)。
(4)对于∀σ∈ε*,轨迹是每个事件只出现一次的一个有限序列,即对于∀1≤i≤j≤|σ|,都有σi≠σj
(5)一组案例L⊆C集合构成了事件日志,其中,对于∀c1,c2,L有c1≠c2:∂set(1)∩∂set(2)=∅, 即每个事件在整个日志中要么不出现,要么只出现一次。
2.1 控制流维度挖掘
在控制流维度,针对遗传过程挖掘算法的不足,提出遗传过程混成挖掘算法。算法的关键在于优质初始种群准备、内部模型的表示方法、综合质量函数的设定以及遗传算子。下面分别说明。
2.1.1 优质初始种群准备
由于初始过程模型的质量越高,则达到高质量模型所需的改变就越少,针对遗传挖掘算法挖掘效率不高的问题,拟对事件日志进行预挖掘,将预挖掘生成的过程模型替代原来随机生成的模型,从而提升GPM算法的初始种群质量。采用IM算法,对于每一个案例,挖掘出所对应的子过程模型。采用该算法的原因是:一方面,IM算法可以得到拟合度80%以上的高质量过程模型,且其算法时间复杂度为多项式时间复杂度,而原有的GPM算法的初始种群是随机生成的,其模型拟合度只有60%;另一方面,IM算法的过程发现架构[7]能够保证挖掘得到的所有模型都具有合理性(sound)[14],即所得模型无死锁及其他异常。由于GPM的算法特性,即每迭代一次,就需要对过程模型种群中所有过程模型进行质量评估和结构改进。如果过程模型不具备合理性,在评估改进之前就需额外进行模型修复,耗时耗力。因而,IM算法对初始种群预挖掘和优化可以提高GPM算法效率[15]。
2.1.2 遗传过程挖掘算法
(1)内部模型的表示方式
由文献[14]可知,Petri网包含了日志中的隐式库所,且对其定义遗传算子较为困难,故使用Petri网作为GPM算法执行内部模型表示法时,可能存在问题。而存在死锁是使用因果矩阵作为内部模型表示法具有的问题,因此,使用过程树作为GPM内部模型的表示方法,其主要优点是该模型是基于块结构的,可以确保模型的合理性[16]。GPM算法需要对过程模型种群中所有过程模型作质量评估和结构改进。由于过程树所具有的合理性和健全性,GPM就不必对不完整的过程模型进行检测及修复。
定义3过程树[17]。过程树是一个三元组PT=(O,L,B),其中:O是非叶子节点,即代表运算符的节点的有限集合;L则是叶子节点,即代表活动的节点的有限集合,使得O∩L=∅;B⊆(O×L)∪(O×O)是有向弧的集合。过程树为一个有向连接图,该连接图不含圆,其第一层节点为(树)根节点,下面各层节点都为对应的上一层节点的子节点(孩子节点)。过程的控制流结构采用运算法节点表示。其结构包括:排它选择×、非排它选择+、顺序结构→、并行结构∧以及循环结构等。
(2)综合质量函数——CQ函数
本文使用以下4个标准进行模型的质量评估,包括拟合度(fitness)[18]、简洁度(simplicity)[17]精确度(precision)[19]和泛化度(generalization)[20]。拟合度是指模型可以反映事件日志中行为的程度,简洁度要求模型可以很好地表达事件日志中的行为且为最简单的模型。精确度和泛化度正好相反,前者避免欠拟合,后者则避免过拟合。然而,4个质量维度相互竞争,尽管目前都有相对应的量化方法,但在他们之间很难达到平衡。同时,多数过程挖掘算法都只能考虑到部分质量指标[16],如基于区域的挖掘算法可以产生拟合度、精确度较好的过程模型,但其泛化度及简洁度较差。然而,4个质量维度都很重要[17],只要一个的值较低,都会影响到最后的挖掘模型。因此,本文提出综合质量(CQ)函数[15],CQ函数可以平衡4个质量维度,也可以在BdSm算法迭代执行过程模型挖掘中对其质量进行监督,最终将CQ作为挖掘导向。
CQ函数的计算公式为:
CQ=(Fr+Pe+Gn+Sm)/4。
式中:Pe,Gn,Fr和Sm分别表示过程模型的精确度、泛化度、拟合度和简洁度;CQ表示模型的综合质量。
(3)遗传算子的过程树表示法
种群中所有过程树的综合质量值,BdSm均使用CQ函数来计算。这个过程中,首先选择出综合质量较高的多个过程树(根据一定的精英选择比例),无需改变地将其保留到下一代,然后对剩余过程树使用遗传操作。为使挖掘结果更好,算法应该通过不断检索的方式来尽量访问更大的搜索空间,这样可以获取具有多样性特征的过程树种群;其次,算法需要使用遗传操作不断提升过程树的综合质量,即过程树种群应当满足“好且不同”的条件。
遗传操作由突变(mutation)、交叉(crossover)和替换(replacement)[21]3个步骤组成。突变可以直接操作节点,提高种群中过程树的质量;交叉随机选择不同过程树之间的两个子树,对它们进行交换,以生成两棵新的过程树;替换则剔除种群中质量最低的一部分过程树,然后使用随机生成过程树代替它们。但这两个操作只能扩大搜索空间,增加种群多样性,并不能直接提升过程树质量。
(4)遗传过程混成挖掘算法框架
遗传过程混成挖掘算法是将过程树集输入,优化整合后的过程模型及其对应的CQ值作为算法的输出结果。算法主要包含4个步骤:
1)初始化。计算所有的过程树的CQ值。
2) 选择。根据一定的比例选择多棵有着最高CQ值的过程树,直接保留至下一代,无需任何其他操作。
3) 繁殖。繁殖操作是通过突变、交叉或是替换操作来改进剩余的过程树。还将设置如“迭代次数”等停止条件,若条件不满足,则迭代进行步骤1)~步骤3)的过程。
4)结束。若停止条件满足,整个算法过程结束。
经过以上步骤,算法在满足停止条件之前多次迭代,每一代种群过程树的质量将不断升高,最终的挖掘结果即为最后一代种群中对应CQ值最高的过程树。图2是遗传过程混成挖掘算法流程图。
参照文献[17],选择操作中,比例参数设置为25%,这些过程树将直接保留不作任何更改;将选择剩余的过程树中前25%的过程树进行突变操作,以提高过程树质量;接着选择剩下的排在前25%的过程树进行交叉操作,以扩大搜索空间及增加种群多样性。在此过程中,综合质量值最低的后25%个体,对其直接使用替换操作进行替换。

2.2 提取组织维度信息
组织维度的信息源于事件日志中的#resource属性,即执行者名称。为将活动与执行者信息更好地关联,探明在执行者层面上活动与活动之间的关系,本文提出活动在执行者层面的距离度量方法。活动之间度量方法基于活动—执行者矩阵,该矩阵记录每个活动被某个特定执行者执行的频率,其中:行对应活动,列对应执行者。抽取事件日志中的活动信息和执行者信息,可获得该矩阵。矩阵中的数值表示某位执行者执行某个活动的次数(如表1)。
定义4活动—执行者矩阵M。设L为事件日志,令a1∈A,r1∈R,c=(c0,c1,c2…)∈L,则:
(1)MC(a1,r1)=
M定义了一个以A为行,R为列的矩阵,矩阵中的数值代表执行者执行活动的次数。

表1 PM组数据活动—执行者矩阵
根据活动—执行者矩阵,通过比较行向量之间的距离,可以计算活动在执行者之间的距离(如表2)。活动之间的距离越近,代表该活动在执行人员配备上越相似。通过探究活动在执行者层面的相似性,有助于了解项目的人员组成,例如,如果CODE活动和TEST活动距离很近,它们皆由编码小组的成员完成,而测试小组的成员较少出现在TEST活动中,则该组织的人员配备可能存在问题需要调整,比如合并两个小组成员或者对编码小组的成员进行划分。在工作任务分配中,如果两个活动距离较近,则可以派遣同样的人员组成去完成两个不同的活动。活动距离表可以记录日志中所有活动之间的距离,该表能够为组织维度提供更多信息。本文使用欧氏距离来度量活动之间的距离。由相同的人执行的活动在执行者层面具有更大的相似性。
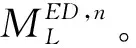

表1是PM组数据的活动执行者矩阵,表2是根据表1的活动—执行者矩阵根据活动欧氏距离计算出的活动之间的距离表。活动到自身之间的距离为0,其中,距离越小,代表活动越相似。

表2 PM组数据活动到活动之间的距离
2.3 执行者信息扩充控制流过程模型
控制流维度最终得到的是以过程树表示的过程模型(如图3)。然而,该过程模型仅能体现活动之间的控制流结构关系。因此,本文在挖掘出控制流过程模型的基础上,添加活动对应的执行者信息。为此,定义执行者过程树,使用组织维度对过程树进行扩展,将活动与执行者进行映射。执行者过程树是BdSm最终的挖掘结果(如图4)。在过程树的基础上添加了每个活动对应的执行人员,执行人员信息从组织维度信息提取得来。执行者过程树组合两个维度,获得全局视角,更直观地反映过程模型在控制维度以及组织维度的信息。算法1是BdSm的部分伪代码。
定义6执行者过程树。执行者过程树是一个五元组PTR=(O,L,B,R,H),其中:(O,L,B)是如定义3中定义的过程树,R为每个叶子节点L对应的执行者的有限集合,H⊆(L×R)是有向弧的集合。其中每个叶子节点对应至少一个执行者。


算法1BdSm遗传挖掘算法。
输入:事件日志L; 迭代次数q; 过程树集ProcessTreeSet={t1,t2,…,tN}。
输出:执行者过程树EPT。
1 foreach (i : [1,2,…,q])
2 foreach (tree: [t1,t2,…tN])
3 CQ (tree); //求每一棵过程树的CQ值
4 sort(tree); //按照CQ值对过程树降序排列
5 foreach (j :[1,2,…,N])
6 Save_1=remain(ProcessTreeSet[1:0.25N]);//对排在前25%的CQ值的过程树无需任何改变直接保留
7 select(ProcessTreeSet[0.25N: 0.5N]);
8 crossover(ProcessTreeSet); //对剩下的排在25%~50%区间的过程树进行交叉操作
9 Save_2=remain(ProcessTreeSet);
10 select(ProcessTreeSet[0. 5N: 0.75N]);
11 mutation(ProcessTreeSet); //再次选择剩下的排在50%~75%区间的过程树进行突变操作
12 Save_3=remain(ProcessTreeSet);
13 select(ProcessTreeSet[0. 75N: 1N]);
14 replacement(ProcessTreeSet); //对最后25%的过程树进行替换操作
15 Save_4=remain(ProcessTreeSet);
16 repeatProcessTreeSet=Save_1∪Save_2∪Save_3∪Save_4;
17 end foreach
18 end foreach
19 end foreach
20 EPT=selectMAX(repeatProcessTreeSet);//选择质量最好的一棵过程树
21 numA=countActivity(EPT); //获取过程树中包含的活动数目
22 foreach (i : [1,2,…, numA])
23 activity[i]=getActivity();
24 end foreach
25 foreach (i : [1,2,…, numA])
26 numE=countExecutor(activity[i]); //获取该活动中包含的执行者数目
27 foreach (j : [1,2,…, numE])
28 getExecuto();//获取执行者名称
29 addExecutor();//添加该执行者
30 end foreach
31 end foreach
32 output (EPT)。//输出执行者过程树
3 实验
3.1 实验数据
为验证所提方法的有效性,本文进行了两组实验:①从功能角度,展示算法在两个不同维度的作用,同时,使用BdSm算法对数据进行挖掘,展示迭代次数随模型质量的变化,观察初始种群优化对最终挖掘结果的影响;②基于4个公开数据集,从挖掘所得模型质量的角度,与其他挖掘算法进行对比实验。
第①组实验使用过程日志生成器(Process Log Generator,PLG)[22]创建模型,如图5所示,根据该模型生成事件日志(简称PM数据)。使用本文方法对事件日志进行挖掘,观察是否能够生成原始模型,以验证方法的有效性,同时分析所生成的双维度模型的含义。图5中共包含7个活动,分别是REQ,DES,TEST, CODE,VER, CONF以及REV,基于过程树表示如图5所示。根据该模型生成20个过程案例。第①组实验中的第2组数据也是由PLG生成的模拟事件日志,记为FW。用于验证控制流维度对生成模型质量的提升。

第②组实验包含4组公开数据集的事件日志。Apache Commons Crypto 1.0.0[23]是一个单元测试软件事件日志,它描述了ApacheCommonsCrypto 1.0.0库的流CbcNopad单元测试套件的一次加密运行。Ticketing Management(TM)[24]是一家意大利软件公司服务台的票务管理流程。Sepsis[25]为由医院的企业资源计划(Enterprise Resource Planning,ERP)系统记录的败血症案例。Bank Transaction[26]为银行交易过程数据。由于部分数据过于庞大,结构复杂,部分过程挖掘算法对其直接挖掘会产生不完备(Unsound)[14]的模型,进而无法进行模型质量评估。因此,本文对事件日志进行过滤,事件日志的大小通常根据4个指标来衡量:案例数目、事件数目、活动数目和案例平均长度(案例中包含事件数目的平均值)[27],最终事件日志的大小和结构如表3所示。

表3 实验中事件日志的大小
3.2 实验方案及参数设置
(1)对PM组事件日志使用BdSm进行挖掘,分别生成活动—执行者矩阵、执行者距离矩阵以及执行者过程树,将PM组数据生成的过程模型与原始模型进行对比。
(2)对PM组、FW组事件日志分别使用GPM和BdSm进行挖掘,对比挖掘获得模型质量与迭代次数的关系。
(3)对PM组、FW组以及4个公开数据集的事件日志分别使用α#算法[28]、IM算法、整数线性规划(Integer Linear Programming,ILP)算法[28]以及遗传挖掘算法(GPM)进行挖掘,计算挖掘所得模型的4个质量维度值以及综合质量,与BdSm的挖掘结果进行对比。
在PM组、FW组以及4组公开数据集事件日志的GPM和BdSm的对比实验中,算法的迭代次数均设置为1 000次,4个遗传突变操作的操作比例一致。并且由于种群数量越少,算法的时间花销就越少[20],GPM的初始种群数量与BdSm中初始种群的数量设置一致,BdSm中初始种群的数目为事件中案例的数目,而对于案例数目较多的情况,本文则使用文献[29]中的方法将相似案例聚类,以确保种群数目保持在合理范围内。
3.3 实验结果
对PM组事件日志生成的20个案例,一方面,对案例分别使用IM算法挖掘,将该挖掘结果作为遗传挖掘算法初始种群,对这些挖掘结果进行优化整合之后得到最终的控制流维度过程模型;另一方面,借助活动—执行者矩阵(如表1)生成活动距离表(如表2),拓展控制流维度模型最终生成执行者过程树(如图6)。

距离越大,则活动在执行者层面越不相似;距离越小,则活动越相似,活动到自身的距离为0。由图4可知,活动DES与REQ的距离最近,这与表1吻合,因为该两个活动由相同两个执行者完成且频率一致。而REQ和CODE的距离较远为8.485,这是由于两个活动没有相同的执行者执行。类似地,结合执行者过程树和活动与活动之间的距离,能得到较多额外信息。
由挖掘结果可以看出,BdSm方法能够挖掘出原始模型,同时,每个活动下连接的人名为该活动的执行者。
图7和图8展示了PM数据以及FW数据由BdSm以及GPM生成的模型随着迭代次数不断增长综合质量变化的情况。由图可见,相对于GPM算法而言,BdSm方法的收敛速度更快,同时达到高质量模型所需迭代次数更少,最终也生成了综合质量更高的模型。PM组中,BdSm方法在77代便已收敛,GPM算法在150代才收敛;FW组中,BdSm方法在359代便已收敛,GPM算法在602代才收敛。由此说明,使用IM算法确实可以为遗传挖掘算法提供更高质量的初始种群,进而加快算法收敛速度,最终生成更高综合质量的过程模型。

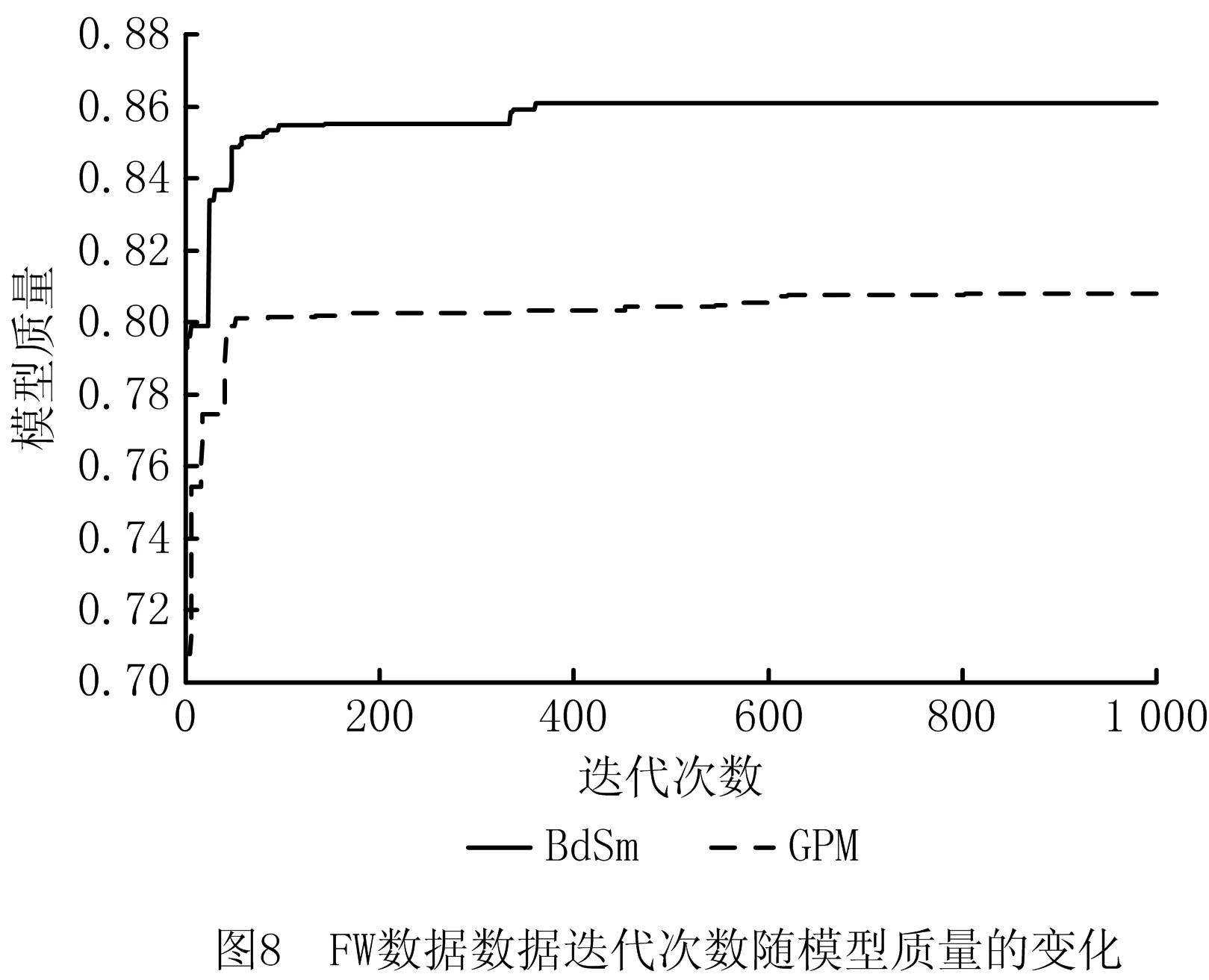
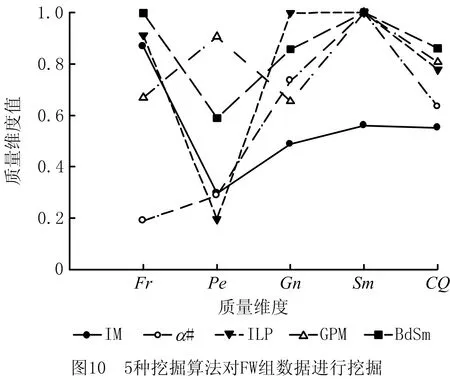
图9~图14展示了6组数据分别用使用IM算法、α#算法、ILP算法、GPM、以及BdSm挖掘生成模型得到的质量,图中不同的折线代表不同的算法。由图可见,使用BdSm对6个数据集分别进行挖掘,所生成的模型呈现以下规律:与其他传统挖掘算法相比,GPM算法以及BdSm方法能够挖掘得到综合质量较高的模型,这是因为遗传挖掘算法通过质量维度指导挖掘的进行,从而生成质量较高的模型。同时,从折线的走势可以看出,相比于其他挖掘算法,BdSm方法挖掘所得模型的4个质量维度值走势较为稳定,折线整体波动幅度不大,这是由于CQ函数为4个质量维度赋予了相同为1的权值,最终BdSm方法挖掘生成模型的综合质量也达到了最高。而对于PM组和FW组而言,事件日志较为简单、数据量较小,因此IM算法、α#算法以及ILP算法生成模型的综合质量都在0.8以上,α#算法、IM算法则达到了较高的拟合度。而对于Crypto 1.0.0组、TM组以及Bank Transaction组而言,由于事件日志较为复杂,算法生成的3种模型的综合质量大幅下降,而只有BdSm方法以及GPM算法生成模型的综合质量能维持在较高水平。最后,IM算法能够产生具有较高拟合度的模型,但模型的简洁度较低;ILP算法挖掘生成的模型具有较高的简洁度和拟合度,但是精确度和泛化度较低。而BdSm方法通过CQ函数作为算法挖掘导向,无论对于哪一个数据集,最终挖掘都能够得到具有稳定的4个质量维度的、综合质量较高的模型。
以上实验结果表明,在控制流层面,BdSm方法能够生成综合质量高于其他挖掘算法的过程模型,究其原因,是遗传过程挖掘算法使用模型质量作为挖掘导向,保证能够生成高综合质量的模型。同时,BdSm方法相对于GPM算法能够更快收敛,且达到更高的综合质量,这是因为使用IM算法为遗传挖掘算法准备了优质种群,初始种群质量越高,则到达高质量模型所需做的改进越少,算法收敛更快。而于GPM算法初始种群随机生成,质量较低,达到较高质量的挖掘结果需要迭代更多次,算法收敛更慢。而在组织维度层面,结合活动之间的距离和执行者过程树,能得到更多组织维度的信息,有助于项目管理者了解人员配备所存在的问题,并进行调整。





4 结束语
本文提出了基于执行者过程树的双维度遗传过程挖掘BdSm方法。在控制流维层面,使用预挖掘的方法为遗传挖掘算法提供优质初始种群,从而加快算法收敛速度,实验证明BdSm方法较其他挖掘方法能够生成综合质量更高的过程模型,且由于使用综合质量函数作为挖掘导向,4个质量维度的值较为稳定,不存在度量值差距较大的情况;在组织维层面,定义执行者过程树,通过在挖掘模型的基础上添加对应执行者信息的方法合并两种维度,且通过模型可以更加直观地看出活动和执行者之间的关系。同时,从执行者层面定义活动之间的距离度量方法,距离更近的活动在执行者配置层面更为相似,从而帮助项目管理者了解和改进组织的人员配备结构。BdSm方法对遗传过程挖掘算法进行改进,通过预挖掘的方法为遗传挖掘算法提供多个初始种群,因此,需要多个案例作为算法的输入,不适用于单案例事件日志的情况。因此,未来将从单案例事件日志入手,对算法进行改进。

