基于MPC模型的滑块轨迹追踪*

石转转，张占东，郭开玺，张榕慧，郝佩儒

(山西大同大学 机电工程学院，山西 大同 037003)

0 引言

在传统的控制方法中，PID作为一种非常经典的控制算法，以其使用简单、调节方便等优势在工业系统应用中占据主导地位，其控制特点是不需要知道系统的模型，仅仅依据目标实际值与期望的偏差进行调节，但PID算法所计算出的控制量经常会有超约束的值，因此，使用该方法无法在控制前期考虑系统的约束[1]。为了克服PID控制算法的这一缺点，在20世纪中后期由Culture等率先提出了一种新型的、基于模型预测的控制方法，即MPC。

模型预测控制(Model Predict Control,MPC)是一种控制多变量系统的技术[2]，其首先在工业控制中被大量应用,经过近几年不断的完善逐渐趋于成熟，随后在其他领域中也迅速得到应用，如汽车、航空航天工业以及智能电网等[3]。

本文基于模型预测控制设计一种控制算法来实现对质量滑块的位置追踪。首先搭建滑块运动学模型，之后基于搭建好的运动学方程，利用模型预测控制理论对滑块整体运动进行分析，最后通过仿真验证所设计控制器的可行性。

1 模型预测控制理论

模型预测控制是一种多输入多输出算法，其基本控制原理如图1所示。在控制过程中有一条参考轨迹即期望轨迹，定义k时刻为当前时刻，并测量出当前时刻的状态值和控制量值，通过预测模型，预测出系统未来p个时域(预测时域)内的输出；求取p个时域内的开环优化问题，得到在k时刻的优化解，但只把优化解的第一个分量作用于系统；在下一时刻k+1，根据新的测量状态重复上述过程，且预测时域滚动向前，不断完成优化问题，从而实现对被控对象的持续控制[4]。

2 控制算法设计

本文主要研究的是质量滑块的位置追踪，是指在无限光滑的一维水平直线上，令滑块的质量为m，初始位置与初始速度都为0的情况下，设计一个控制器，利用传感器测得滑块位移x，并在此基础上为滑块提供外力u，使其能够跟随参考点xr。

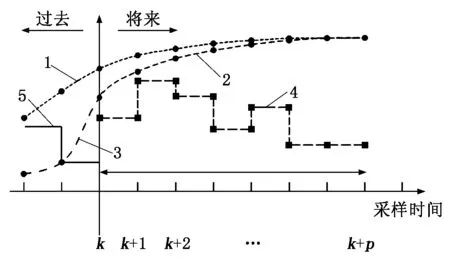
1-参考轨迹;2-预测输出;3-测量输出;4-预测控制量;5-已执行控制量

2.1 运动学模型的建立

在MPC的控制策略下，以滑块为研究对象，被控量为外力u，首先建立动力学方程：

(1)

(2)

2.2 模型离散化

在上述建好的状态方程(2)的基础上，设k为当前采样时刻，k+1为下一采样时刻，T为控制周期。利用前向欧拉法可得到离散系统状态方程:

(3)

移项得：

农村电网的整体结构是供电的基础，对于这方面，首先要把握好主干网架的建设情况。然后，要考虑到连线的安全接入方式。要充分以安全为核心，提高整体带来的供电能力。同时要针对一些突发的状况作出合理的防护措施，比如电杆位置的选择和电杆深度的考虑。建成之后，以110kV为中心，10kV专业辅助的整体要基本实现。

x(k+1)=(I+TA)x(k)+TBu(k).

(4)

其中：I为单位矩阵。

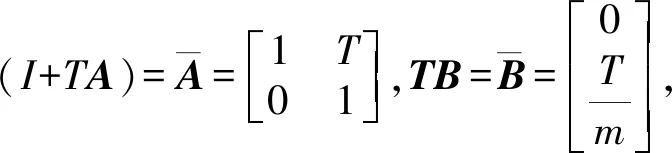
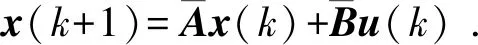
(5)

速度v作为系统输出，输出方程可表示为:

(6)

2.3 预测模型

MPC控制理论中，预测的基本思路是用当前的状态和输入预测下一个状态并确定预测时域、控制时域。即定义k时刻为当前时刻，预测接下来p个时域内的状态，从k时刻到k+p时刻[5],并记未来p个控制时域内预测的系统状态为：

Xk=[x(k+1|k)Tx(k+2|k)T…x(k+p|k)T]T.

(7)

式(7)中，(k+1|k)表示根据k采样时刻的信息来预测k+1时刻的值，以此类推到k+p。当要对动态系统未来状态进行预测时，还应求得整个预测时域内的控制输入量Uk，即为后续将要求解的优化问题的独立变量：

Uk=[u(k|k)Tu(k+1|k)T…u(k+p-1|k)T]T.

(8)

接下来通过离散化状态方程依次对未来p个控制周期的系统状态进行预测，可以得到：

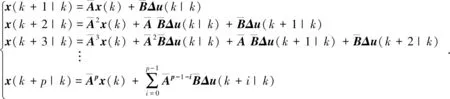
(9)

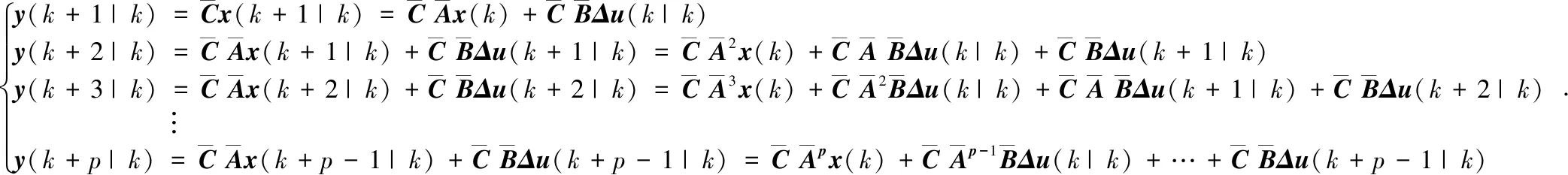
(10)

系统的控制时域为n。想要让系统关系愈加明了，则未来时刻的输出可以整合成矩阵的形式表达：

Yk=Ψx(k)+ΘΔUk.

(11)

其中：

通过式(11)可看出，利用系统当前的状态量x(k)和控制时域内的控制增量ΔUk可以计算出预测时域内的状态量和输出量，实现模型预测控制算法中的“预测”功能。同时由Θ可知，矩阵为下三角形式，可以得出：k+1时刻的输入对k时刻的输出没有影响，k+2时刻的输入对k和k+1时刻没有影响。

3 二次在线滚动优化

每个采样时刻的优化均可得到一系列控制序列，但只将优化解的第一个元素作用于系统，然后在下一采样时刻将新得到的测量状态值作为初始条件，重新进行优化。同时，随着当前时刻的向前推移，预测时域也在向前滚动[6]。

由于外部干扰和模型失配的影响，系统的预测输出和实际输出会存在偏差，若在下一时刻，根据测量到的偏差值在线求解控制输入Uk，即可优化掉这个偏差值[7]。为了让实际输出轨迹追踪预先设定的参考轨迹，定义预测时域内的参考序列：

Rk=[r(k+1)Tr(k+2)T…r(k+p)T]T.

(12)

最佳的控制输入值实际是使得图1当中系统参考轨迹曲线与预测输出曲线越接近越好。因此，用预测输出与参考值之间的累计误差定义一个优化目标函数：

J(Uk)=(Yk-Rk)TQ(Yk-Rk).

(13)

通常不希望控制动作变化太大，对优化目标函数再添加一项对控制量的约束：

(14)

其中:Q和W为权重矩阵。

因此，该优化问题可以描述如下：

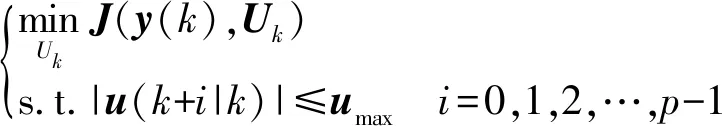
(15)

令E=Ψy(k)-Rk，再将优化函数J(Uk)展开后合并同类项得：

(16)

调用MATLAB中的QP即二次规划求解器quadprog进行求解，令:

(17)

(18)

得到最终优化目标函数：

(19)

4 仿真分析

为了验证MPC控制器的可行性，利用MATLAB/Simulink搭建仿真平台，实现质量滑块的位置追踪控制。

将方程(1)两边同时进行拉普拉斯变换得：

(20)

即可得到传递函数：

(21)

在Simulink中搭建仿真环境,如图2所示，同时编写MPC控制器。

图2 仿真环境

本文所研究滑块的质量设定为1.05 g，其中0.05 g为建模误差。通过给定不同的预测时域值来对滑块位置追踪状况进行对比分析。当控制周期为0.01 s时，将预测时域分别设置为p=20、p=30、p=45、p=53、p=60，在此参数下的滑块模型预测位置追踪仿真结果如图3所示。由仿真结果可知，当给定的预测时域值越大，系统的状态便能够对期望的轨迹进行更加平稳的追踪。

图3 滑块模型预测位置追踪仿真结果

5 总结

本文提出了基于模型预测控制的滑块轨迹追踪控制方法，以质量滑块为研究对象，对其进行理论分析，建立运动学模型，通过仿真分析验证了方案的可行性。