基于新型小波阈值函数的降噪方法研究*
徐方素,孙兴伟,董祉序,王海燕,杨赫然
(1.沈阳工业大学 机械工程学院,辽宁 沈阳 110870;2.沈阳白云机械有限公司,辽宁 沈阳 110027)
0 引言
实际工程中,信号在采集、传播和处理过程中常常受到噪声的污染,导致质量退化,需要对其进行降噪处理[1]。传统的信号降噪方法分为空间域降噪和变换域降噪[2,3],在众多降噪方法中,小波阈值降噪算法由于具有去相关性、多尺度、多分辨率等特性得到了广泛应用[4]。
传统的硬阈值收缩方法存在不连续和不稳定的现象,且对信号中的微小变化较敏感,导致其降噪效果欠佳,而软阈值收缩方法由于具有较好的连续性,降噪效果明显提升,但在小波系数收缩过程中会出现恒定偏差,导致其对信号细节信息的扼杀现象[5]。本文针对以上问题,在现有研究基础上提出了一种新型小波阈值函数,并通过仿真对本文方法的降噪性能进行验证。
1 新型小波阈值降噪方法
1.1 传统小波阈值降噪方法
一个含有噪声的一维小波信号表示如下:
f(t)=s(t)+e(t).
(1)
其中:s(t)为原始信号;e(t)为服从N(0,σ2)分布的高斯白噪声;f(t)为含噪信号。
(1)硬阈值函数表示为:

(2)
(2)软阈值函数表示为:
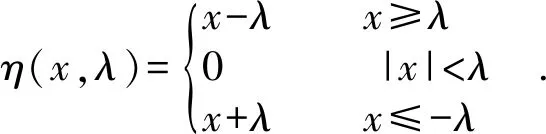
(3)
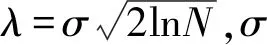
虽然传统小波阈值方法在信号降噪方面有一定效果,但仍存在一些明显缺陷:硬阈值函数导致重构信号产生波动,影响降噪效果;软阈值函数具有很好的连贯性,降噪效果显著,但其处理后的小波系数和原始小波系数之间存在恒定偏差,从而影响重构信号和原始信号的逼近程度,最终导致信号边缘失真。
1.2 一种新型小波自适应阈值函数
针对上述传统小波阈值函数存在的缺点,同时为了使阈值函数在实际应用中具有自适应性,本文在保留传统阈值函数优点的基础上,构建了一种含有调节参数的新型小波自适应阈值函数:
(4)
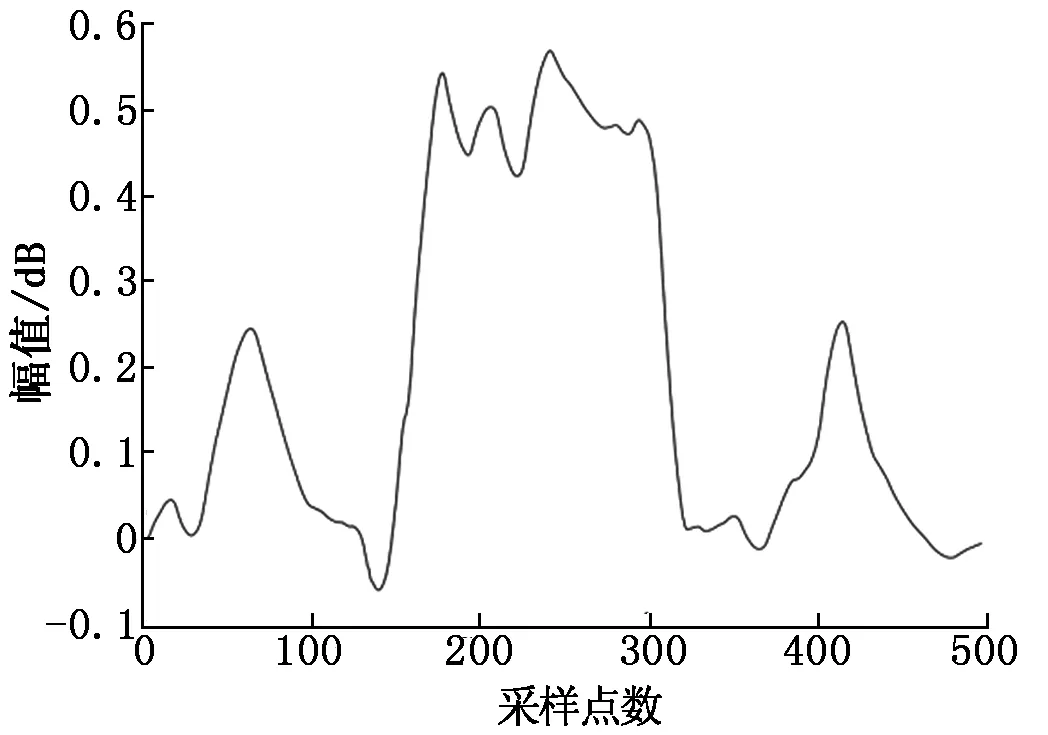
其中:a、b、m为调节因子,a和b(a>0,b>0)为新型阈值函数的两个形状控制参数,m(0 分析上述函数形式和参数变化可知,构建的新型阈值函数具有高阶可导性质和小波系数自适应收缩能力,不仅可以增强小波降噪能力,而且可以改善对混叠在随机噪声中真实数据的扼杀现象。 仿真验证采用一组叠加了高斯白噪声的含噪信号,信号采样点数为500,含噪信号如图1所示。分别应用传统的硬、软阈值函数以及本文构造的自适应阈值函数对图1中的信号进行降噪处理。选择sym4小波对信号进行4层分解;选择启发式阈值规则(Heursure准则)。采用不同阈值函数小波降噪后的结果分别如图2~图4所示。 图1 含噪信号 图2 软阈值函数降噪后的仿真信号 图3 硬阈值函数降噪后的仿真信号 图4 新型阈值函数降噪后的仿真信号 为了精确比较传统的软、硬阈值函数与本文阈值函数的降噪效果,引入统一的客观评价标准。本文根据信噪比(Signal to-Noise Ratio,SNR)和均方误差(Mean Squared Eror,MSE)两个降噪性能评价指标来定量分析: (5) (6) 降噪完成的信号信噪比值越大、均方误差越小表明降噪完成的数据与原始数据更为接近,同时具备更好的降噪效果。采用三种阈值函数降噪后的评价指标具体数值如表1所示。 表1 不同阈值函数降噪结果对比 对比图2~图4可以发现:软阈值函数降噪能力较强,降噪信号较平滑,但其对数据中真实细节信息的扼杀也较为严重;硬阈值函数降噪能力较差,波形存在一些波动,不能很好地过滤掉随机误差,降噪效果并不明显,信号中还存在明显的噪声;本文提出的新型小波自适应阈值函数则成功地解决了上述问题,提高了信号的重构精度。另外,由表1中数据可以看出,应用本文提出的新型小波自适应阈值函数对含噪信号降噪效果明显优于传统阈值函数。 为了弥补现有小波阈值降噪算法的不足,本文构造了一种带有形状参数和逼近参数的双曲正切函数作为阈值函数,仿真结果表明,新型阈值函数具有高阶可导性质和小波系数自适应收缩能力,不仅显著提升了小波阈值降噪能力,而且较好地保持了真实信号的细节信息,具有较广阔的工程应用前景。2 仿真验证



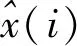

3 结论

