应用集对分析数学模型对给水管网综合水质的模拟分析
王丹宁,赵洪宾,袁 渊,刘 贝
(1. 中建三局工程设计有限公司,浙江杭州 310006;2. 哈尔滨工业大学市政环境工程学院,黑龙江哈尔滨 150090)
改善水质的研究一般都集中在给水厂的净化工艺上,但供水从水厂到用户需经过给水管网进行输送,供水水质在管网中会发生一系列的变化。给水管网的水质污染往往易受到忽略,从水厂供水泵房到用户水表要途经庞大的给水管网,情况错综复杂,供水管道长度有些长达数十公里,供水在管网中的停留时间,从几小时甚至长达数天不等。
管网类似一个巨大的反应容器,供水在里面发生物理、化学、微生物学等一系列反应,致使给水在管网中发生了不同程度的水质变化,使水受到二次污染,水质水平及等级呈下降趋势,这样即使出水厂达标了,但经过管网输送到用户处的水也往往达不到国家饮用水标准。
在管网中经过变化的不合格供水送到用户,会对人的健康产生不利影响,因此,给水管网中的水质研究就显得尤为重要。管网中某监测点的综合水质是通过多项水质评价指标的整体情况确定。评价监测点的综合水质需先建立数学模型,通过对其模拟计算可把每个监测点的整体水质情况数据化,以此确定其综合水质等级[1-6]。
1 集对分析数学理论
集对分析是处理随机复杂变化问题的一种重要数学理论。该理论研究不确定性对象具有独特优势,能从整体和局部上进行研究。集对分析的数学模型是建立2个集合间,通过对2个集合同一性、差异性、对立性进行研究,最终以量化的数值精确地反映出二者的联系程度。该理论广泛应用于环境、水资源、信息系统、经济学等各个领域[7]。
2 给水管网水质分级
水质分级就是按照规定的标准,划分不同水质指标的界限取值,对水质的情况进行评价。我国对生活饮用水的评价制定了相关标准,如《城市供水水质标准》(CJ/T 206—2005)、《生活饮用水水质标准》(GB 5749—2006),但其中都没有明确分级标准。
2002年颁布的《地表水环境质量标准》(GB 3838—2002),依据地表水水域环境功能和保护目标,按功能高低依次划分为5类,为地表水评价提供科学的参照依据。《农村实施〈生活饮用水卫生标准〉准则》中对生活饮用水的等级分为3级,一级为期望值,二级为允许值,三级为缺乏其他可选择水源时的放宽限值。
参照地表水分级的先进理念并吸取农村生活饮用水分级的经验,在给水管网水质综合评价中引入分级的概念,以便对水质的好坏进行区别划分。
3 给水管网水质综合评价集对分析数学模型
集对分析理论基本表达式如式(1)。
u=a+b1i1+b2i2+…+b(k-2)i(k-2)+cj
(1)
其中:a——实测值与一级的联系度系数;
b1——实测值与二级的联系度系数;
b2——实测值与三级的联系度系数;
b(k-2)——实测值与k-1级的联系度系数;
i(k-2)——实测值与k-1级标准值的联系度变量符号,具体联系度取值为其系数;
cj——实测值与k级的联系度系数。
式(1)表示标准值与实测值之间的联系程度,a、b、c三者之和为1。标准共分为K个等级,好于或与一级相同时a取1,u=1;与k级相同或比k-1级差时c取1[7],u=j。
给水管网中的水质会随机变化,这是诸多水质指标共同作用的结果。将集对分析理论应用到给水管网中,建立水质综合评价的集对分析数学模型,通过模拟计算,可把管网中监测点的综合水质的数据赋予量化,为判断水质等级提供精确的科学依据。
将给水管网监测点中样本水质评价指标的实测值与其分级标准值作为2个集合进行分析。赵克勤[7]将给水管网中的分级标准、样本、水质评价指标等因素与集对分析表达式进行融合,袁绍国等[8]整理给水管网水质综合评价的集对分析数学模型。
本文结合集对分析理论,并参考前人研究成果,构建给水管网水质综合评价集对分析数学模型。给水管网中水质分为K个等级,给水管网监测点样本共有N个,水质评价指标共有M个。选取给水管网中第n个监测点样本的第m个评价指标作为研究对象,二者之间的联系度数学模型如式(2)~式(6)。经模型模拟计算,可判定二者的联系度,结合评价指标所占的权重比,最终判定给水管网监测点综合水质的等级[8-10]。
unm=1+0i1+0i1+…+0ik-1+0j(0 (2) (3) (4) (5) unm=0+0i1+0i2+…+0ik-1+1j(Sk (6) 其中:S1——评价指标的第一级标准值,S2、S3定义以此类推; m——第m个评价指标; xnm——第n个样本、第m个评价指标的实测值; unm——第n个样本、第m个评价指标实测值与1至k级标准值的联系度; i1——实测值与二级标准值的联系度变量符号,具体数值为其系数; ik-2——实测值与k-1级标准值的联系度变量符号,具体联系度取值为其系数; j——实测值与k级标准值的联系度变量符号,具体联系度取值为其系数。 (7) (8) (9) 其中:ωm——第m个评价指标的权重系数; am——第m个评价指标实测值与一级标准值的联系程度系数; bm(k-2)——第m个评价指标实测值与k-1级标准值的联系程度系数; cm——第m个评价指标实测值与k级标准值的联系程度系数; un——第n个样本的k元联系度; Rn1——第n个样本的与一级标准的联系度; Rn2——第n个样本与二级标准的联系度; Rnk——第n个样本与k级标准的联系度。 客观权重参考文献[11-12]中客观权重的方法计算如式(10)~式(11)。 (10) (11) 其中:dm——第m个评价指标的水质单因子指数; sm——第m个评价指标的水质标准值; xm——第m个评价指标的水质实测值。 特殊单因子取值:当细菌总数≤3 CFU/mL与大肠菌群数≤3个/L时,水质单因子指数取0.1;当pH符合标准时,水质单项指数取0.1;当色度<15时,水质单因子指数取0.1;当浑浊度<1 NTU时,水质单因子指数取0.1。 在某地给水管网中设置监测点,监测点中各项水质指标数据传递到处理中心,利用集对分析数学模型进行模拟计算,得到该点综合水质的量化数据,依据此数据判定其水质等级,并对异常监测点进行处理。本文选取给水管网中1个监测点的数据进行分析,水质评价指标选取具有代表性的10项。 水质评价指标分级标准值的确定参照《生活饮用水水质标准》(GB 5749—2006)、《城市供水水质标准》(CJ/T 206—2005)及《农村实施〈生活饮用水卫生标准〉准则》,如表1所示。S1、S2、S3分别表示水质评价指标第一、二、三级的标准值。 表1 给水管网综合水质评价指标分级标准值Tab.1 Grading Standard Value of IWQ Evaluation in WSDN 水质评价指标的实测值、标准值客观权重值如表2所示。 表2 给水管网综合水质评价指标实测值、标准值、客观权重Tab.2 Measured Value, Standard Value and OW Value of IWQ Evaluation in WSDN 客观权重计算中,以色度计算为例,特殊单因子取值,当色度<15时,水质单因子指数取0.1。依据式(10)~式(11),单因子指数之和为5.868,ωm=0.1/5.868=0.017。 本实例中监测点样本n为1,水质评价指标m取1~10。水质评价指标序号为1、2、3、7、9、10的实测值在0 表3 监测点样本计算结果Tab.3 Sample Calculation Results of Monitoring Points 根据表2的客观权重值,结合式(8)运算,则监测点1的计算表达式为u1=0.648 1+0.351 9i1+0i2。利用式(8)~式(9)计算,运算过程如式(12)~式(13),得R11=0.648 1,R12=0.351 9,R13=0。 R11=0.017×1+0.017×1+0.017×1+0.18×0.74+ 0.256×0.25+0.181×0.70+0.102×1+0.196×0.70+ 0.017×1+0.017×1=0.648 1 (12) R12=0.017×0+0.017×0+0.017×0+0.18×0.26+ 0.256×0.75+0.181×0.30+0.102×0+0.196×0.30+ 0.017×0+0.017×0=0.351 9 (13) 结合模拟后的运算结果(表3)进行分析,第1个样本的第1、2、3、7、9、10个评价指标色度、浑浊度、pH、氯化物、细菌总数、总大肠菌群与第一级的联系度均为1。第1样本的第4、5、6、8个评价指标总硬度、铁、硫酸盐、溶解性总固体与第一级的联系度分别为0.74、0.25、0.7、0.70,第1个样本的第4、5、6、8个评价指标与第二级的联系度分别为0.26、0.75、0.3、0.3。 10个水质评价指标中,6个指标好于一级标准值或符合一级标准值,其他4个指标实测值处于一级和二级之间,除序号5的硫酸盐实测值与第一级的联系度为0.25,其余3个指标与第一级的联系度分别为0.74、0.7、0.7,与一级的联系度高于与二级的联系度。 水质指标中与一级联系度较高的分别是色度、浑浊度、pH、细菌总数、总大肠菌群,与二级联系度较高的分别是铁、溶解性总固体、硫酸盐、总硬度。各个水质指标的客观权重不同,客观权重数值大的水质指标实测值影响大于权重数值小的指标。由表2可知,几个水质指标的客观权重数值较大,按数值从高到低排序,依次是表2中序号5、8、6、4、7水质指标,这些指标对计算结果影响较大,其余水质指标客观权重数值较小,对计算结果影响也较小。 综上,利用集对分析数学模型进行模拟运算,得到监测点综合水质处于一级与二级之间,与一级水质的联系度为0.648 1,与二级水质的联系度为0.351 9,与三级水质的联系度为0,偏向一级的程度高于偏向二级的程度。 通过构建给水管网综合水质的集对分析数学模型,可精确、有效地计算出监测点的综合水质量化数据,判定其水质等级,并与实测数据进行对比验证,证实可利用集对分析数学模型反映给水管网中监测点综合水质状况及等级。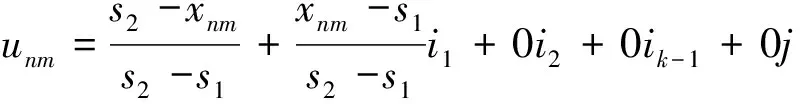
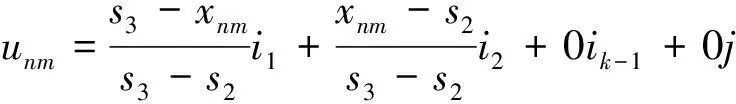


4 实例模拟计算
4.1 实例选取
4.2 水质评价指标标准值、实测值

4.3 水质评价指标客观权重

4.4 集对分析计算

4.5 计算结果分析
5 结论

