中等应变率下玻璃纤维-环氧树脂复合材料层合板强度预报

吴 健，王纬波，张彤彤，李泓运

（1.海军工程大学船舶振动与噪声重点实验室，武汉 430033；2.中国船舶科学研究中心船舶振动噪声重点实验室，江苏 无锡 214082）

0 引 言

纤维增强复合材料因其独特的力学特性，在航空、航天等领域得到了广泛的应用。复合材料在船舶领域应用时不可避免地遇到冲击、碰撞等问题，需要深入研究中等应变率下的复合材料力学性能，船舶结构在多种载荷条件下的应变率一般小于100 s-1[1]。

自从Hayes等发现很多情况下复合材料的力学性能明显依赖于应变率以来，国内外一些学者便致力于高应变率下复合材料的力学性能研究。Wang等[1-2]给出了单向玻璃纤维增强复合材料纤维方向的准静态～80s-1下的中等应变率测试结果，提出了一种粘弹性的本构模型；Tsai等[3-4]研究了应变率对多种偏轴角下单向复合材料剪切性能的影响，建立了剪切强度与应变率的关系；Brown等[5-6]通过不同的试验方法研究了纤维织物增强复合材料在中等应变率下的拉伸、剪切、压缩等性能，建立了剪切强度与应变率的关系；Ryou等[7]采用Instron高速测试系统开展了玻璃纤维编织复合材料的中等应变率下力学行为研究，获得了中等应变率下力学性能参数，用于穿刺仿真时与试验吻合较好；Kwon等[8]基于层合板理论及多种角度试样的应变率试验结果，提出了一种预测碳纤维增强层合板模量的模型，但未开展层合板强度预报研究。关于纤维增强复合材料力学性能的应变率效应研究逐渐深入，已经朝着性能预报与结构动态性能分析的方向发展。

Tsai-Hill强度准则[9]是适应于各向同性材料的von Mises屈服准则在正交各向异性材料中的推广，该准则综合考虑了材料的3个主方向应力与相应基本强度的交互作用对材料破坏的影响。原则上，Tsai-Hill准则只适用于拉压强度性能相同的复合材料。蒋邦海等[10]在准静态和动态压缩实验的基础上，拟合出了屈服应力和压缩破坏强度与应变率相关性表达式，考察了Tsai-Hill屈服强度和破坏强度准则随应变率的变化规律；Schaefer等[11]针对IM7/8552复合材料提出了一种渐进式失效框架来描述试验结果从线性到非线性的变化，建立考虑应变率效应的Northwestern理论作为失效准则开展强度预报，该方法对角铺层层合板适用性较好；谈炳东等[12]基于正交各向异性单向板的Tsai-Hill强度准则，引入率相关函数法和率强度因子法改进，预测短纤维增强三元乙丙薄膜在不同偏轴方向下的抗拉强度。但由于试验条件的限制，实际加载应变率仅达到0.04 s-1。吴义韬等[13]对复合材料宏观强度准则进行了总结和评述，认为各准则均有一定的不足，只有不断发现和总结复合材料的损伤规律，才能建立更为合理的强度准则，进而指导复合材料结构设计与分析。王力立等[14]对典型复合材料强度准则的预测能力和适用性进行了评估分析和总结，即使综合排名第一的准则也仅有35%的预测结果在±10%误差范围内，预测精度与刚度退化模式、材料本构模型等有关。复合材料静强度的预报较为复杂，由于动态测试技术的限制，有关复合材料层合板在应变率条件下的动态力学性能预报的研究还不多。

通过中等应变率下单向复合材料层合板的面内拉伸、剪切性能试验测试，获得不同应变率下单向板的基本强度破坏参数，建立相应的拉伸和剪切强度数学模型。进而以经典层合板理论和蔡-希尔强度准则为基础，实现了玻璃纤维-环氧树脂复合材料层合板在中等应变率下的强度性能预报，为中等应变率下复合材料层合板铺层方案性能优化提供一种方法。

1 考虑应变率效应的层合板强度分析

1.1 单向板材料性能

单向板的坐标系与材料主方向一致时，应力和应变之间关系的表达式为

假设第k层单向板的材料主方向与x轴的夹角为θ，则总体坐标系与局部坐标系的转换矩阵为

1.2 经典层合板理论

考虑N层任意铺设的单向板构成的层合板，如图1所示。取z轴垂直于板面，xoy坐标面与中面重合，板厚为t。根据弹性力学，板中任意一点的位移分量u、v、w可以表示为

图1 复合材料层合板的坐标系Fig.1 Coordinate system of composite laminate

根据经典层合板的基本假设，可得

经过推导可以得到由层合板的中面应变和曲率表达的第k层应力

进而得到作用层合板上的合力

式（7）可以改写为

1.3 考虑应变率效应的强度准则

以往的经验结果表明蔡-希尔破坏准则与试验结果吻合较好，可以作为玻璃纤维-环氧复合材料的判据[15]，其表达式如下：

式中：X、Y、S为单向板的破坏强度参数；σ1、σ2、τ12为单向板中应力值。从式（10）可以看出，蔡-希尔破坏准则仅需获得三个单向板的破坏强度参数，试验测试成本和难度相对较低，这是选用其进行预报分析的重要原因之一。

考虑应变率对强度的影响时，第k层板的破坏强度参数可以表示成与应变率相关的函数：

当整体复合材料层合板的应变和应变率是已知的，那么在每一单层中的应变和应变率都可求得。

通过应变率转换公式求得的各层单向板的应变率应取准静态应变率和计算应变率中的较大值，准静态应变率取为0.000 3 s-1。

2 试验方案设计

2.1 试验装置

文中使用的力学性能设备为MTS公司的370.10型材料试验机及Instron公司的VHS 80/100-20型高速测试系统。静态力学性能试验主要由370.10型材料试验机完成，包括静强度、模量、泊松比等参数，如图2所示。

图2 静态力学性能测试Fig.2 Static mechanical performance test

图3所示为高速测试系统，该高速测试系统采用压电式力传感器，可以实现最高20 m/s的加载速度，可以研究材料在恒定应变率条件下材料的力学行为。

图3 高速测试系统Fig.3 High speed test system

式中，ε˙x为试样的轴向应变率，t为时间，V为试样加载速度，L为试样的标距。

2.2 材料与试样

为了适应高速测试系统的高速夹具，试样采用文献[16]中夹持端粘贴钢片的结构形式。静态拉伸试验采用引伸计测量应变，高速试验采用日本KYOWA公司的KFG-10-C1型应变片测量应变，测量泊松比使用KFG-1-D16型应变花测量纵向和横向应变。

3 复合材料单向层合板板性能测试结果

3.1 拉伸性能测试

采用[0°]10铺层的试样进行轴向拉伸测试，获得不同应变率条件下的轴向应力与应变关系。不同应变率下的平均轴向应力应变曲线见图4，拉伸模量和强度的试验结果见表1。

图4 不同应变率下[0°]10试样的拉伸应力应变曲线Fig.4 Tension stress-strain curves of[0°]10 specimens under different strain rates

表1 不同应变率下[0°]10试样的拉伸性能试验结果Tab.1 Tension properties of[0°]10 specimens under different strain rates

从表1中可看出，应变率对玻璃纤维/环氧复合材料强度影响较大，而对模量影响不大，已有的文献研究结果也表明单向玻璃纤维增强复合材料模量不受应变率影响[1]，表1中模量测试结果出现差别的原因可能是采用了应变与载荷测试原理均不同的两套设备。

为了减小模量值对后续分析的影响，采用下式描述应力和应变之间的关系：

为了便于程序插值求解不同应变率下的拉伸强度，采用下式描述应变率和拉伸强度之间的关系：

图5 拉伸强度与应变率的关系Fig.5 Relationship between tensile strength and strain rate

纤维增强复合材料的泊松比一般不受应变率影响[17]，因此通过静态轴向拉伸试验测得单向板的泊松比ν12为0.31，通过[90°]10试样静态拉伸试验测得E2为4.9 GPa，平均强度为15.4 MPa。

理论上应该考虑90°方向的材料强度的应变率效应[8]，由于采用纯单向纤维，90°方向无承受载荷纤维，试样安装过程中特别容易损坏试样，且90°方向的强度值较低，无法达到高速试验机的载荷有效测量范围，无法通过测试得到相应的数据，因此本文后续分析过程中暂时忽略了90°方向的强度应变率效应。

3.2 剪切性能测试

采用[±45°]8s铺层的试样进行轴向拉伸测试，并通过应力变换得到不同应变率条件下的剪切应力-应变关系，见图6。

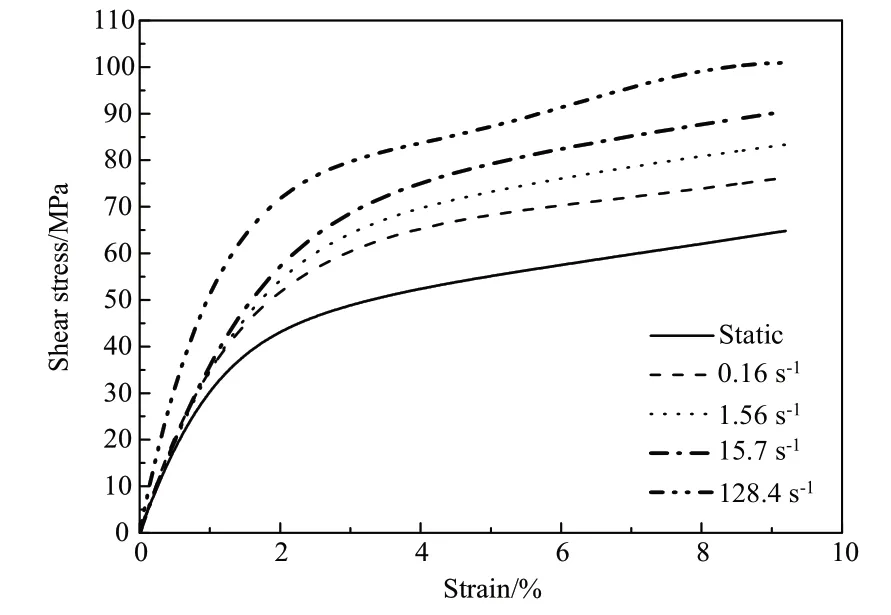
图6 不同应变率下[±45°]8s试样的剪切应力应变曲线Fig.6 Shear stress-strain curves of[±45°]8s specimens under different strain rates

目前一致认为±45°拉伸剪切试验不能测定真正的材料极限剪切强度，文献[18]建议采用5%剪应变下的剪应力或破坏前的最大剪应力中较小值来代替“极限剪切强度”，因此表2中剪切强度为5%剪应变条件时的剪切应力。对于剪切模量，后续分析时取前四组应变率测试结果的平均值。

表2 不同应变率下[±45°]8s试样的剪切性能试验结果Tab.2 Shear properties of[±45°]8s specimens under different strain rates

为了便于程序插值求解不同应变率下单层板的剪切强度，利用下式描述剪切强度和应变率的关系[16]：

式中，C和D为系数，S0为准静态的剪切强度。通过最小二乘法进行数据拟合，当系数C取29.37、D取0.457 7时，拟合曲线能够很好地反映剪切强度与应变率的关系，如图7所示。

图7 剪切强度与应变率的关系Fig.7 Relationship between shear strength and strain rate

4 复合材料层合板强度研究

4.1 中等应变率下层合板强度预报

根据经典层合板理论公式和考虑应变率效应的蔡-希尔强度准则编制MATLAB计算程序，计算步骤如图8所示。

图8 中等应变率下层合板强度预报流程Fig.8 Strength prediction process of laminates under intermediate strain rate

当计算程序中应变率取0时，预报过程退化为准静态拉伸强度评估问题，可利用文献[15]中准静态算例来验证程序的正确性。算例1：[0°/90°5]S铺层的层合板承受面内轴向拉力Nx；算例2：[-15°/15°/-15°]铺层的层合板承受面内轴向拉力Nx。单层材料是玻璃纤维/环氧，其性能参数为E1=53.74 GPa，E2=17.95 GPa，ν12=0.25，G12=8.626 GPa，Xt=1.034 GPa，Yt=0.027 GPa，S=0.041 GPa。仿真结果与算例结果的对比如图9所示，图9（b）中结果偏差来源于算例计算过程中的数据四舍五入。

图9 仿真结果与算例结果对比Fig.9 Comparison of simulations and examples

图10 不同应变率下层合板强度的预报曲线Fig.10 Shear stress-strain curves under different strain rates

4.2 试验验证

图11 应力-应变预报曲线与试验对比Fig.11 Stress-strain curve of prediction and test

图12给出了不同试验速度下的位移-载荷对比，可以明显看出震荡幅值随着试验速度的增加而增大。但是预报和测试结果的趋势依然吻合较好，说明考虑应变率效应的蔡-希尔强度准则对上述材料铺层方案适用性较好，第3章中采用5%剪应变下的剪应力来代替“极限剪切强度”是合理的。

图12 不同试验速度下的位移-载荷对比Fig.12 Displacement-load curves under different test speeds

拉伸强度的对比结果如表3所示。可以看出，预报结果值均大于试验测试值，且偏差随着应变率的增加而增大，平均偏差在12%左右，接近于文献[14]中铺层标识II和III的无缺口板拉伸强度预报的精度。参考世界范围内的复合材料失效分析竞赛中的评分规则[20]，强度预测值和试验结果的偏差在±10%～±20%之间可计为B。分析认为误差主要来自以下几方面：（1）强度准则输入参数较少，但这也是本方法的一个优势；（2）加工成条状试样时，切割损伤及边缘效应导致的试验结果偏小；（3）动态试验时，随试验速度增加引入了较强的震荡信号，导致强度结果取值存在偏差。考虑到动态测试的测试方法和传感器精度等级，认为文中预报方法可以满足工程应用需求。

表3 拉伸强度预报结果与试验结果的对比Tab.3 Tensil strength comparision between prediction and test

5 结 语

本文基于中等应变率条件下的单向板的强度数据，采用经典层合板理论和蔡-希尔强度准则预报了玻璃纤维-环氧树脂基复合材料层合板的拉伸强度，预报精度满足工程应用的需求。该方法可用于复合材料层合板的铺层方案优化。

剪切强度对预报结果影响较大，采用5%剪应变下的剪应力来代替极限剪切强度是降低误差的一个重要措施。

后续将开展90°方向的材料强度的应变率效应测试研究，进一步完善应变率条件下的复合材料强度模型。