限制区域水面无人艇路径规划与跟踪控制研究
刘正锋,张隆辉,魏纳新,匡晓峰
(中国船舶科学研究中心,江苏 无锡 214082)
0 引 言
水面无人艇(Unmanned Surface Vehicle,USV)作为一种无人化与智能化作战平台,在军用和民用领域都有着广泛的应用前景。从目前的发展趋势来看,无人艇技术研究的重点在于确保无人艇能够在包含静态和动态障碍物的复杂海域环境下安全、有效地自主航行。路径规划及路径跟踪控制是无人艇自主航行的前提,是无人艇智能化程度的重要体现,同时也是迫切需要解决的关键技术问题。
路径规划属于无人艇任务规划的底层问题,包含两种类型:一种是环境信息已知的全局路径规划;另一种是基于传感器信息的局部路径规划。常用的规划方法有启发式搜索算法[1-2]、人工势场法及智能规划算法等。Dijkstra算法是一种早期的路径搜索算法,其速度较慢,研究人员又发展了A*算法及其改进算法,提高了计算速度。然而这类方法所得的路径距离障碍物太近,会影响无人艇自主航行的安全。人工势场法[3-4]的原理是将目标点视为吸引子,而将障碍物看为斥力点,无人艇沿着引力与斥力的合力方向前进,该方法明显的不足是存在局部“陷阱”,在障碍物前会产生振荡,因此人工势场的设计是算法能否应用成功的关键。智能规划算法[5-7]随着人工智能技术的发展取得了长足的进步,比较典型的有粒子群算法、遗传算法及一些混合改进算法等,规划路径通常是一条较为光滑的曲线。当地图信息复杂时,规划路径会出现较多的航向改变点,导致无人艇路径跟踪时需进行较为频繁的操舵控制,间接地影响无人艇自主航行的安全性能。概率地图法(PRM)[8-12]是一种基于采样的图形算法,通过在规划环境中随机设置路标点,从起始点出发,在保证不与障碍物相交的前提下将当前点与所有临近点用直线段连接,构成初始路径图;然后运用优化算法对初始路径图进行查询搜索,从而获得从出发点到目标点满足优化目标的优化路径。该方法可以很好地解决高维空间中路径规划问题,其算法的复杂度主要来源于搜索路径图的难度,环境范围以及空间维度影响不大,并且计算量较小,具有较好的实时性,在机器人任务规划以及无人机路径规划中得到了广泛的应用。基于概率地图法良好的工程应用特性,本文将该方法应用到水面无人艇的路径规划中。
跟踪控制的主要目的是保证无人艇按照路径规划设计的期望路径航行。水面无人艇在复杂的海洋环境中航行时,由于船舶自身的欠驱动特性,对操纵性能、控制特性以及可靠性提出了更高的要求。从20世纪90年代起,国内外学者对水面无人艇的欠驱动控制问题[13-15]进行了深入研究。研究的主要方法包括Backstepping设计法、Lyapunov直接法、模糊控制、滑模控制、预测控制等,其中预测控制以其在约束控制问题处理上的优势而广受关注[16-18]。Li等[19-20]在加强横摇约束时,考虑舵机饱和约束和运动速率约束,利用MPC实现了对四自由度水面船舶的航迹跟踪问题。Oh等[21-22]在欠驱动船舶跟踪轨迹过程中先利用视距导引法对航路点跟踪问题建模,同时设计航路点跟踪的导航和控制系统,通过求解线性约束优化问题来提高路径跟踪控制器的性能;Zheng等[23]基于非线性模型和连续线性化后的水面船舶分别设计了MPC控制器,研究了水面船舶的约束轨迹跟踪问题,验证了MPC对船舶轨迹跟踪的有效性,特别是处理约束的能力;Zhang等[24]考虑了横摇约束限制,设计了预测控制器,研究了受外界载荷干扰下的欠驱动水面船舶路径跟踪问题。上述工作大多是针对预设路径开展的跟踪控制器的设计,没有考虑限制区域航行时航迹规划的实现及影响,但是这些研究工作为水面无人艇路径规划后跟踪控制器的设计提供了很好的参考。
水面无人艇的路径规划和路径跟踪是密切联系的,路径规划需要考虑无人艇自身运动控制的特性,同时规划路径需要通过路径跟踪来实现。因此,本文针对限制区域水面无人艇的路径规划与控制技术进行研究,首先利用概率地图法在限制区域进行路径规划,然后通过模型预测控制完成无人艇对规划路径的跟踪控制。
1 基于PRM的无人艇路径规划
概率地图法通过构造自由空间中的连通图,将连续空间的规划问题转换为拓扑空间的规划问题,问题求解的复杂度主要依赖于路径搜索复杂度,而与整个规划环境的复杂度以及规划空间的维度无关。基本的PRM算法分为两个阶段:概率地图的构建以及路径的查询搜索。首先,PRM算法在自由空间内(图1)基于某种概率分布进行空间采样生成路径点V(图2),并将这些采样点与它们的邻居节点进行互联构建地图中的边集E(图3),从而构成代表自由空间的概率地图R;然后从起始点开始在概率地图中进行搜索,找出一条连接起始点和目标点的可行路径(图4)。PRM算法的实现流程如图5所示。

图1 规划空间示例Fig.1 Illustration of planning space

图2 随机采样点分布Fig.2 Sampling points in planning space
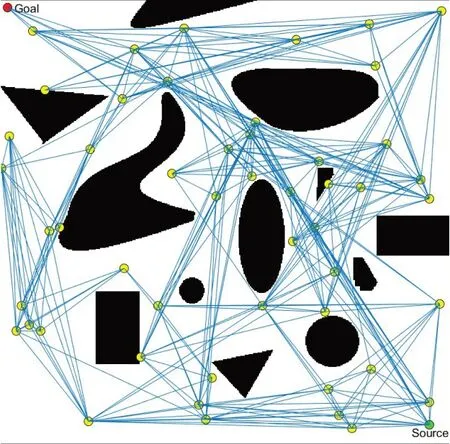
图3 邻近点连接得到的路径段Fig.3 Feasible edges of neighboring points

图4 路径搜索结果Fig.4 Planning path output

图5 概率地图算法流程图Fig.5 Flow chart of probabilistic roadmap method
在构建概率地图过程中,边集通过局部规划器完成。局部规划器是一个高速的、作用单一的规划单元,它将符合某种衡量准则的两个采样点连接起来。衡量准则通常基于两方面的要求:一是两点之间距离与设定阈值的比较;二是两点之间线段不能与障碍物发生碰撞。在可行路径的查询搜索阶段,运用优化方法对地图边集进行搜索,从而得到一组由边构成的从出发点到目的点并满足优化目标的路径。如果起始点和目标点不存在相连路径,则重新回到路径图构建阶段,进行节点增强以提高路线图在复杂区域的连通性,并重新规划直至输出可行路径。
概率地图方法实现简单,且具有良好的工程实用性,因此本文将该方法应用到水面无人艇路径规划中。水面无人艇在航行时会受到水域的限制威胁,如暗礁、浮标、移动的船只等,路径规划的主要目的就是在地图空间内寻找初始点到目标点并避开障碍物的可行途径。为简化问题,用圆形或由相交圆构成的区域将障碍物覆盖,这也为利用概率地图法在处理包含复杂外形障碍物区域路径规划问题时提供了合理的便捷条件。因此,本文在进行路径规划研究时直接用圆形障碍物代替。另外,在水面无人艇路径规划过程中,为保证规划路径的可行性与有效性,需要对障碍物进行膨胀处理,膨胀半径可以采用无人艇的回转半径代替,也可以根据航行环境要求进行设置。结合无人艇的操纵性能要求,为保证路径跟踪控制过程中水面无人艇艏向不会发生大幅度的改变,需要提高规划路径的工程实用性,本文给出两种处理方法:(1)PRM方法路径规划的结果与采样点的分布相关,考虑到该方法效率高,可以在规划空间内进行路径点多次采样及路径规划,并在规划路径中比较寻优,选择适应度更优的规划路径作为目标路径;(2)在路径查询搜索时需要加以约束,可以设置路径线段方向变化的阈值范围,搜索下一路径线段时,仅保留与当前路径方向偏差在阈值范围内的线段,以确保规划路径的方向角不发生剧烈的变化。
为验证限制区域内PRM方法在无人艇路径规划中的效果,假设规划空间范围为500×500,在此范围内随机生成50个障碍物,考虑边界影响膨胀后的圆形半径取为10,无人艇起始点位置为[10,10],目标点位置为[490,490],路径规划结果如图6~9所示。

图6 传统PRM方法的可行路径Fig.6 Feasible paths by classic PRM
图6给出了利用传统PRM规划出的10条可行路径。可以看出,PRM产生的规划路径是由一系列直线段组成,每一条路径都能保证无人艇从出发点到达目标点,并且都能有效避开障碍物。但是,部分单次规划出的可行路径航线方向会出现急剧的变化,最大约为116°,这显然不利于无人艇的路径跟踪控制,在工程实际中不适用,需要剔除。为避免这一问题,我们可以进行多次规划,选取适应度更优的规划路径。图7给出了图6所示的10条可行路径中以路径最短为评价指标的寻优结果。显然,最短路径更为平滑,航线方向不会出现大幅度变化,最大约为45°,有利于无人艇的路径跟踪控制。
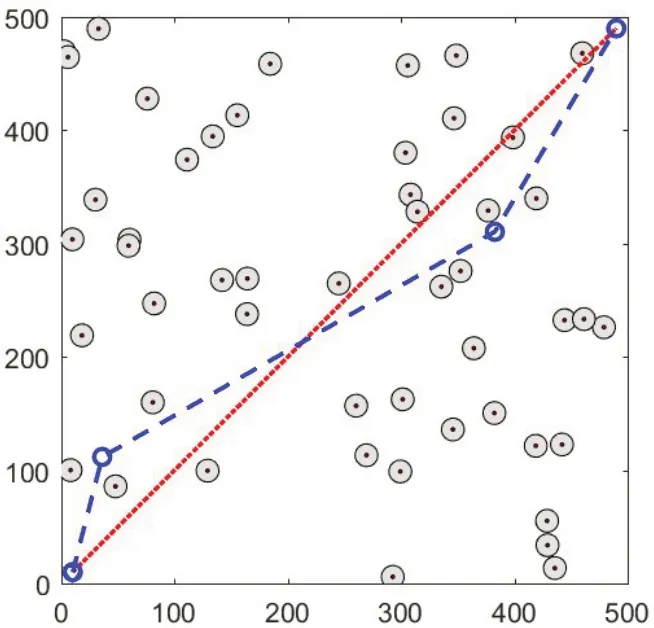
图7 当前最短路径Fig.7 Current shortest path
图8给出了考虑航线方向约束(航线方向变化量不超过45°)的10条规划路径。可以看出,各可行路径航线段的方向变化均在允许范围内平滑地过渡到下一航线段,都适合作为无人艇的跟踪路径。以路径长度作为适应度指标来评价,最短路径如图9所示,该路径更为平滑,且整段路径仅出现一个航向改变点,航线方向变化约为10°,可以选为无人艇跟踪控制的目标路径。

图8 考虑航线方向约束的规划路径(Δψk≤45°)Fig.8 Feasible paths considering route direction constraint(Δψk≤45°)
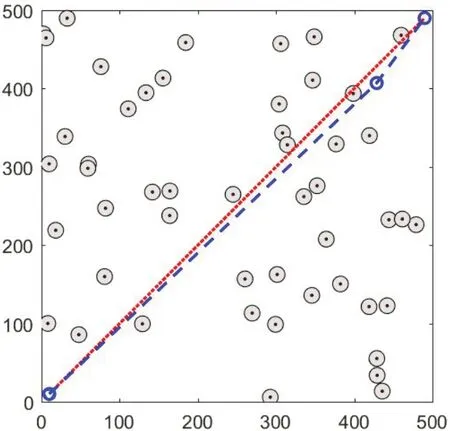
图9 考虑约束的最短路径(Δψk≤45°)Fig.9 Shortest path considering route direction constraint(Δψk≤45°)
从上面的示例可以看出,概率地图法可以成功地应用于限制区域内水面无人艇的路径规划,规划路径由一系列直线段组成,便于实现水面无人艇路径跟踪控制。此外,通过多次规划寻优或者加入航线方向约束限制,规划所得路径的适应度更优、更平滑,更有利于无人艇的跟踪控制,可以作为无人艇跟踪控制的最终目标路径。
2 路径跟踪控制
2.1 数学模型
无人艇路径规划完成后,需要设计跟踪控制器来控制无人艇的运动从而实现规划路径的跟踪。实际海况中水面船舶的运动非常复杂,就路径跟踪控制问题而言,仅需考虑纵向、横向以及艏摇运动,可将问题简化为三自由度水平面运动控制问题。对于欠驱动水面无人艇而言,路径跟踪主要通过舵的控制使无人艇从起始位置沿着设计路径航行,在此过程中可以忽略时间和航速的控制问题,着重考虑操舵对无人艇艏向的控制。通常情况下,艇体对操舵的响应是一种缓慢的运动,可以用野本方程来描述。考虑艏向控制时非线性的影响,野本方程形式如下:

式中,K和T分别为无人艇的回转性指数和操纵性指数,α为非线性模型系数,ψ为无人艇艏向角。

参考图10所示的坐标系,当前航线段PkPk-1的方向ψk可以表示为

图10 路径跟踪示意图Fig.10 Sketch of path following

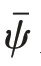
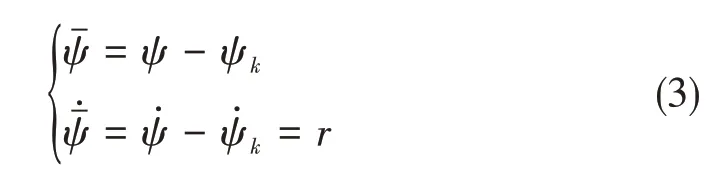
无人艇的位置在当前航线段上可以表示为

对式(5)两边求导可得

无人艇航行速度U在惯性系和艇体坐标系中满足如下关系:

跟踪过程中不考虑纵向运动的控制,可以忽略操舵对无人艇航速的影响。考虑简化,假设u=U,v=0,代入式(6)可得

结合操舵运动响应方程式(2),最终可得无人艇路径跟踪的数学模型为

2.2 模型预测控制

路径跟踪数学模型式(10)的标准形式如下:


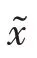
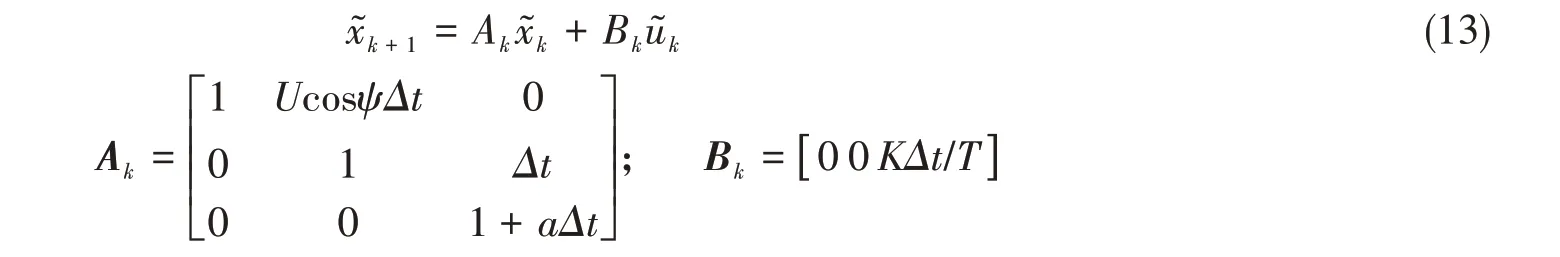
参考模型预测控制建模方法,定义二次型性能函数J为

式中,N为预测范围,Q和R分别为权重矩阵。约束条件包括:

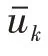

式中:



3 仿真分析
为综合验证限制区域内水面无人艇路径规划及跟踪控制的效果,进行了数值仿真试验。限制区域范围为1 000 m×1 000 m,在此范围内生成50个随机障碍物,考虑边界影响膨胀设定障碍区域半径范围[15 m,40 m]来模拟不同尺度的障碍物。限制区域环境如图11所示,无人艇起始点位置为[10 m,10 m],目标点位置为[990 m,990 m]。路径跟踪控制过程中的主要仿真参数如表1所示。

图11 规划空间Fig.11 Planning area

表1 主要运动参数Tab.1 Motion parameters
设计的模型预测控制器中,预测范围取为N=50,权重矩阵选取Q=diag{[1,1,1]},R=1,无人艇舵角的控制采用优化求解的第一个指令分量执行。在路径跟踪控制时,不失一般性考虑,可令初始艏向指向目标点。另外,为确保航线段切换顺利,设定一个阈值范围(本文取为3L),当无人艇进入路径转向点的阈值范围内时,跟踪路径切换为下一航线段直至无人艇到达目标位置。
首先在模拟的限制区域环境中进行路径规划寻求无人艇从起始位置到达目标位置的目标路径。图12给出了不考虑航线方向约束和考虑航线反向约束两种情形,通过PRM多次规划寻优比较后所得的最终目标路径,分别记为Path1和Path2。
图12的结果表明,两条路径均可以保证从起始位置避开障碍物到达目标位置。不考虑航线方向约束的目标路径(Path1)长度约1 447 m,整体路径由两条直线段组成,存在一次航线方向改变,角度大约为35°;考虑航线方向约束的目标路径(Path2)长度约1 400 m,整体路径由三条直线段组成,存在两次航线方向改变,角度变化量最大值约为20°,即相对而言,目标路径Path2路径长度更短而且显得更为平滑,更有利于进行跟踪控制。

图12 路径规划结果Fig.12 Path planning results
下面分别对以上两条目标路径,利用模型预测控制器对水面无人艇进行跟踪控制仿真。图13~15为无人艇对目标路径1进行跟踪控制的结果,图16~18为无人艇对目标路径2进行跟踪控制的结果。

图13 路径1跟踪控制Fig.13 Path1 following control

图14 路径1跟踪误差时历曲线Fig.14 Path1 cross tracking error

图15 路径1跟踪舵角指令Fig.15 Rudder control in Path1 following

图16 路径2跟踪控制Fig.16 Path2 following control
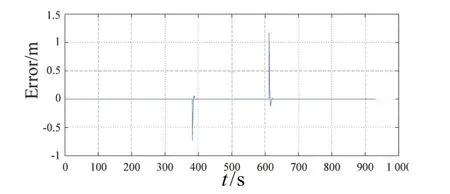
图17 路径2跟踪误差时历曲线Fig.17 Path2 cross tracking error
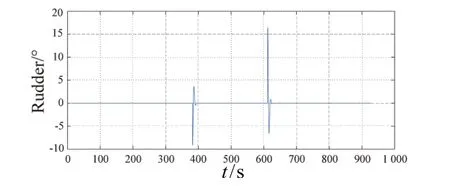
图18 路径2跟踪舵角指令Fig.18 Rudder control in Path2 following
仿真结果表明,在模型预测控制器作用下,水面无人艇通过对舵的控制,可以快速平稳地逼近并收敛于跟踪路径,最终实现对目标路径Path1和目标路径Path2的跟踪。文中所示的路径跟踪过程中,Path1大约耗时960 s,Path2约耗时930 s。
图14和图17分别给出了路径Path1和路径Path2跟踪控制过程中的路径偏差曲线。路径跟踪过程中,由于无人艇到达转向路径点需要进行航线段的切换,实时路径误差由当前无人艇位置与下一航线段的偏差决定,所以在显示图中会出现跳跃信号,并非控制过程不稳定。无人艇对两条路径跟踪控制过程中的操舵指令分别如图15和图18所示。不难看出,舵角指令的触发点对应于跟踪路径的切换转向点。从目标路径Path1和Path2的跟踪效果局部对比可以看出,路径2比路径1更平滑,整个跟踪控制过程中位置误差相对较小,并且能更快速地收敛于目标路径,这也说明了目标路径2更适合作为路径跟踪控制的目标路径。
4 结 论
本文介绍了对限制区域水面无人艇路径规划与跟踪控制的研究。该研究利用概率地图法在限制区域内进行路径规划,并设计模型预测控制器对目标路径进行跟踪控制,将无人艇的路径规划和跟踪控制有机地结合起来。算例仿真分析结果表明:
(1)概率地图法可以成功地应用于限制区域内水面无人艇的路径规划,规划路径由一系列直线段组成,有利于对水面无人艇进行路径跟踪控制器的设计;同时,通过多次规划、增加航线方向角度约束限制等,可以提高PRM规划路径的工程实用性;
(2)考虑路径跟踪控制的特殊性,采用线性化操舵响应模型所设计的模型预测控制算法,可以快速平稳地实现欠驱动水面无人艇对目标路径的跟踪控制。
本文工作为限制区域内水面无人艇的路径规划和跟踪控制技术研究提供了一条行之有效的实施途径。需要指出的是,PRM规划出的路径依赖于采样点在规划空间的分布。因此,PRM规划通常得不到最短路径,但是PRM可以在短时间内规划出多条可供选择的可行途径以及次优路径。在实际工程中,无人艇路径规划与跟踪控制还需考虑限制水域内动态障碍物的影响、外界环境条件的影响以及突发事件的影响,这要求路径规划具有更为快速高效的响应能力。另外,在路径跟踪控制时,舵机控制除了饱和舵角约束还需考虑转舵速率的约束,这些内容有待于在以后的工作中进一步研究。

