砾石覆盖粒径对土壤入渗过程的影响

吕文聪,邱 阳,谢忠奎,王新平,王亚军

(1.中国科学院 西北生态环境资源研究院,兰州 730030;2.中国科学院大学 中丹学院,北京 100049)

土壤入渗是指水分从土壤表层向土壤内部渗透的过程，是土壤水分运动过程中的一个重要阶段。我国西北黄土高原地区生态环境极其脆弱，水土流失严重，每年水土流失量为4 400～7 600 t/km2[1]。黄土高原水土流失常伴随着土壤养分的大量流失，破坏了整个土壤微环境，对土壤质量产生不利影响[2]。在这种条件下，当地居民提出了砾石覆盖这种独具旱作农业特色的耕作方法，即用不同粒径的砾石和粗砂覆盖在农田土壤表面，可以减少土壤蒸发和地表径流，提高水分利用效率，为植物生长提供更适宜的环境，在旱作农业生产中得到了广泛和长期的应用[3-7]。《甘肃农村年鉴2017》记载，甘肃境内的砂田面积在2016年底已达到7.2万hm2，约是1949年的2.4倍[8]。

储存在土壤中的水分可通过毛细管孔隙上升到地表从而蒸发[9]。砾石覆盖土壤表面后，建立起一道天然屏障，防止土壤表面和空气的接触，有效抑制土壤水分蒸发。砾石覆盖也可以使土壤免受雨滴的溅蚀，从而防止土壤表面密实[10]，进而保持和提高土壤入渗性能；砂石也会嵌入土壤，减少入渗[11]，使覆盖土壤的入渗过程较裸土更为复杂。砾石覆盖主要通过影响地表粗糙度、有效孔隙数量、过水断面大小和土壤水分运移通道等土壤物理特征来改变土壤入渗[12-14]。具体影响则与砾石粒径、覆盖厚度、覆盖位置、覆盖度及土壤砾石含量有关[15]。党宏宇等[16]采用一维垂直定水头法模拟了不同煤矸石覆盖厚度及位置条件下土壤的入渗规律，结果表明当煤矸石位于上层时，稳定入渗率、平均入渗率和累积入渗量随煤矸石厚度的增加呈增大趋势；煤矸石位于中层时，土壤水分的入渗过程受到抑制；煤矸石位于下层时，煤矸石对土壤水分入渗过程影响较小。白一茹等[17]通过室内土柱模拟试验研究砾石覆盖层厚度对土壤水分入渗的影响，发现砾石覆盖显著提高了土壤入渗速率，且入渗速率和累积入渗量均随着覆盖层厚度的增大而增大。王小燕等[18]通过人工模拟降雨试验研究了坡耕地5个不同砾石覆盖度(0%，11%，20%，33%和42%)对土壤入渗过程的影响，指出稳定入渗速率及稳定入渗系数与砾石覆盖度呈正相关。李雪垠等[19]指出在同一粒径砾石覆盖条件下，土壤的初始入渗率、平均入渗率、稳定入渗率和累积入渗量都随砾石含量的增大而降低。但是，关于土壤表面覆盖不同粒径砾石对土壤入渗变化规律的研究分析缺乏。研究砾石粒径对覆盖土壤入渗的影响对覆盖土壤耕作和管理具有十分重要的意义。因此，我们在前人研究的基础上，利用室内土柱模拟试验研究分析不同粒径砾石覆盖对土壤湿润锋运移深度、初始入渗率、稳定入渗率和入渗总量的影响，探究砾石粒径与入渗总量之间的关系，以期为砾石覆盖土壤的水量平衡提供科学依据，为干旱区农业保水措施的改善提供理论支持。

1 研究区概况

试验在中国科学院西北生态环境资源研究院皋兰站进行(甘肃省兰州市皋兰县，北纬36°13′，东经103°47′)。皋兰站海拔高度约为1 800 m，位于黄土高原和内陆侵蚀高原之间的过渡带，且过渡带位于水蚀和风蚀系统之间的交错区域。皋兰县年平均降水量为263 mm，降水年内分布不均，变化较大，70%的降水集中分布在每年的6—9月份。该区域的年平均温度为7.1℃，月平均最低温度为-9.1℃(1月)，月平均最高温度为20.7℃(7月)，≥0℃的年积温为3 324.5℃。该区域的平均日照时数为2 768 h。土壤为在黄土母质上发育的灰钙土，在中国土壤系统分类中为简育雏形干旱土。土壤有机质含量1.0%～1.1%，全氮0.07%～0.09%，全钾1.98%～2.10%，速效磷7～10 mg/kg，速效钾120～160 mg/kg。机械组成中粉砂粒占60%左右，物理性黏粒只占24%～35%，0—150 cm土壤容重1.20 g/cm3。

2 材料与方法

2.1 供试样品

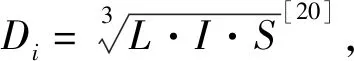
表1 所选的砾石粒径分布特征

2.2 试验装置

土壤入渗试验装置由圆形土柱、供水装置(马氏瓶)、夯土器等组成。土柱为有机玻璃柱，厚度为1 cm，内径为16 cm，高度为100 cm，其最底层散布若干个直径为2 mm的细孔用于排水。马氏瓶为内径16 cm，高100 cm，厚1 cm的有机玻璃柱，为降低积水水头变化对入渗过程的影响，所有处理的供水水头均控制在4～5 cm。

2.3 试验方法

2019年12月在试验室内进行不同粒径砾石覆盖土壤的入渗试验，试验方法采用一维垂直定水头法。在土柱最底层覆盖5 cm厚2～5 mm粒径的砾石并在其上盖一层滤纸以防土壤颗粒落入。将风干的土样按照1.3 g/cm3的容重分层(每层5 cm)装入土柱中，为防止分层，用毛刷将土层间打毛。装填到45 cm后，将等效粒径分别为8.28，16.38，26.36，38.39 mm的砾石按7 cm厚度覆盖在土壤表层，共4个处理，其中无砾石覆盖为对照(CK)。试验设3个重复。试验结束后，取3个重复的平均值进行数据分析和作图。

试验开始后，同时读取马氏瓶中水位高度及土柱中湿润锋运移深度，前5 min，每1 min记录1次；5～30 min内，每5 min记录1次；30～120 min内，每10 min记录1次；120 min后每30 min记录1次。湿润锋运移深度选取土柱圆筒四周可见湿润区的最远位置，直到湿润锋运移至土柱最底层为止。

2.4数据处理

初始入渗率取计时1 min时的入渗速率。稳定入渗率取50～120 min内记录的8个入渗率的平均值。用SPSS 20.0进行数据分析。利用Origin Lab 2018绘制相关图表、拟合Kostiakov，Horton及Philip入渗模型。统计变量均用均值±标准误差(SE)表示。使用单因素方差分析(ANOVA)和LSD显著差异检验在p<0.05(LSD 0.05)水平下分析数据。

3 结果与分析

3.1 砾石覆盖粒径对湿润锋运移的影响

图1为不同粒径砾石覆盖土壤的湿润锋深度随入渗时间的变化过程。由图1可知，覆盖砾石后土壤湿润锋的运移特征发生明显变化，且不同砾石粒径处理之间湿润锋深度随时间的变化特征有所差异。所用处理湿润锋向下移动的深度均随时间而逐渐增加，但向下移动的速度都在减小。与CK相比，砾石覆盖明显增加了湿润锋推进速度，且湿润锋的推进速度随砾石粒径的增加而明显加快。以入渗历时30 min为例，砾石覆盖粒径8.28，16.38，26.36，38.39 mm的湿润锋运移距离分别是21.9，22.3，23.85，24.43 cm，均高于 CK的运移距离17.96 cm。可知随着砾石覆盖粒径的增加，湿润锋运移速率明显加快，即砾石覆盖粒径与湿润锋运移深度呈正相关。

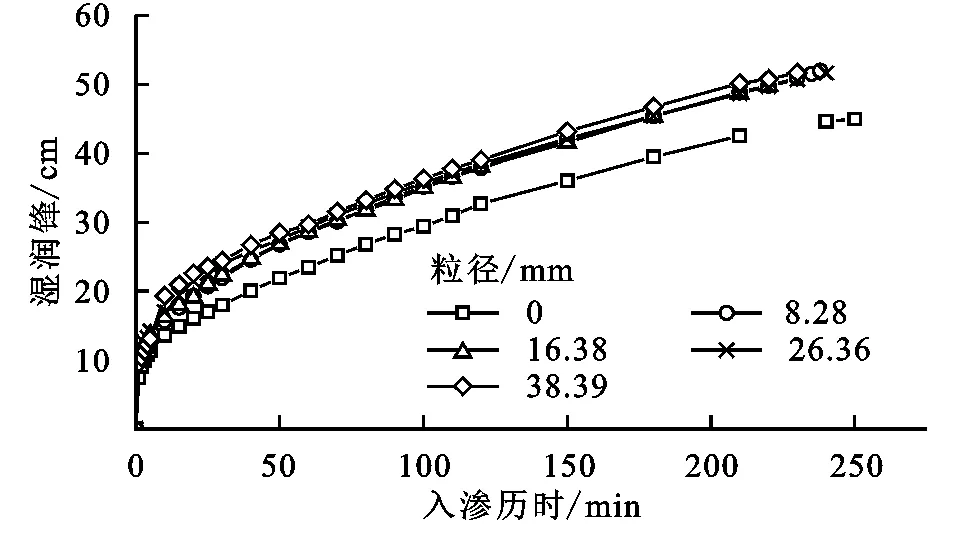
图1 不同粒径砾石覆盖湿润锋随时间的变化过程

为了进一步研究砾石粒径对湿润锋运移的影响，根据湿润锋随时间的变化趋势，采用幂函数F=atb对湿润锋运移的变化过程进行拟合。式中：F为湿润锋运移深度(cm)；t为入渗历时(min)；a，b为经验系数。拟合结果见表2。其中a表征计时1 min后的湿润锋运移深度；b表征湿润锋进程的衰减程度。表2中的拟合结果说明幂函数可以很好地拟合不同粒径砾石覆盖下土壤的湿润锋运移特征，各处理的决定系数(R2)均大于0.986。在湿润锋运移深度随时间变化的过程中，随砾石覆盖粒径的增大，a呈上升趋势，b为下降趋势，即初始湿润锋运移深度增大，衰减速率减缓。

表2 幂函数拟合不同粒径砾石覆盖湿润锋随时间变化过程的结果

3.2 砾石覆盖粒径对土壤水分入渗性能的影响

图2显示了不同粒径砾石覆盖土壤入渗率随时间的变化过程。土壤入渗初期，入渗速率迅速下降，随着入渗时间的延长，入渗率下降的速度逐渐减缓，各处理土壤都在20～30 min左右趋于稳定，达到稳定入渗阶段。土壤水分入渗过程可以分为入渗率迅速下降、入渗率下降速度逐渐减缓和入渗率趋于稳定3个阶段。

图2 不同粒径砾石覆盖入渗率随时间的变化特征

初始入渗率、稳定入渗率和入渗总量是土壤水分入渗的重要特性。由表3方差分析结果可知，砾石粒径对初始入渗率有显著影响。砾石覆盖粒径为8.28，16.38，26.36，38.39 mm的初始入渗率相对于CK分别显著增加了0.6，1.01，1.33，1.81倍(p<0.05)。同时也发现，砾石粒径对稳定入渗率和入渗总量有一定的影响。与CK相比，砾石覆盖粒径为8.28，16.38，26.36，38.39 mm的稳定入渗率分别增加了0.07，0.08，0.16，0.18倍，入渗总量分别增加了0.08，0.11，0.18，0.25倍。

表3 不同粒径砾石覆盖土壤的入渗特征

由表3和图3看出，砾石覆盖下，入渗总量从小到大为17.33 cm(CK)，18.68 cm(粒径8.28 m)，19.18 cm(粒径16.38 mm)，20.45 cm(粒径26.36 mm)和21.68 cm(粒径38.39 mm)。与CK相比，覆盖砾石粒径26.36 mm和38.39 mm显著增加了土壤入渗总量，且这2个砾石粒径在曲线上重叠较多，说明较大粒径砾石对土壤水分入渗的促进程度相似。将4种不同砾石粒径和入渗总量建立关系，见图4。从图4可以看出，随着砾石粒径的增大其土壤入渗总量以直线形式上升，变化幅度为4.34 cm，相关方程为：y=0.103x+17.69(R2=0.983)，即入渗总量与覆盖砾石粒径呈正相关关系。

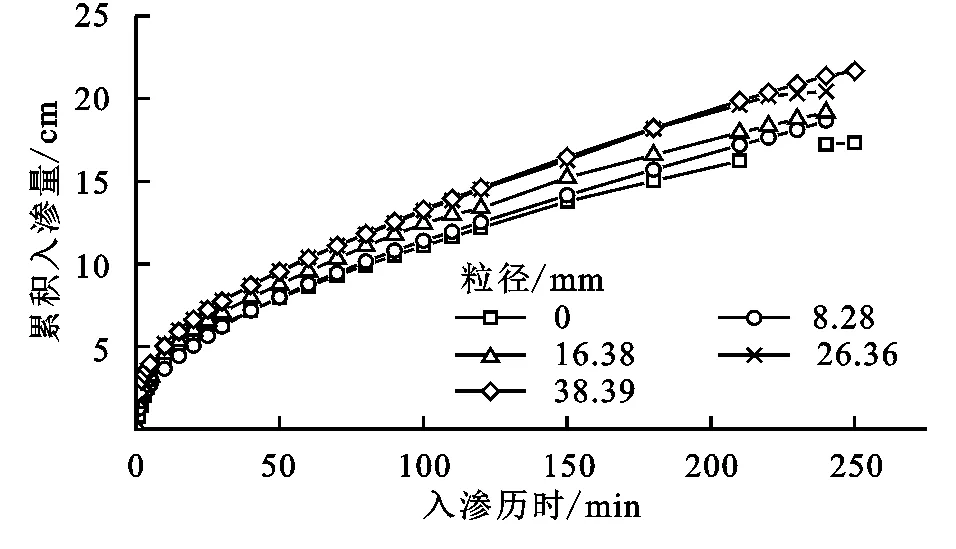
图3 不同粒径砾石覆盖累积入渗量随时间的变化过程

图4 砾石粒径与入渗总量的关系

3.3 土壤入渗过程模型分析

为了进一步研究覆盖砾石粒径对土壤水分入渗过程的影响，采用Kostiakov，Horton及Philip入渗模型对不同粒径砾石覆盖的土壤水分入渗速率随时间变化过程进行拟合分析，其表达式如下

Kostiakov模型：

F(t)=at-α

(1)

式中:F(t)为入渗速率(cm/min);t为入渗历时(min);a,α为根据试验求得的模型参数。

Horton模型：

F(t)=fc+(f1-fc)e-bt

(2)

式中:F(t)为入渗速率(cm/min);t为入渗历时(min);f1为初始入渗率(cm/min);fc为稳定入渗率(cm/min);b为试验求得的参数。

Philip模型:

F(t)=0.5St-0.5+A

(3)

式中:F(t)为入渗速率(cm/min);t为入渗历时(min);S为吸渗率(cm/t0.5);A为稳定入渗率(cm/min)。

表4显示各土壤入渗模型的拟合结果。在Kostiakov模型的拟合结果中，参数a，α的值均随砾石粒径的增大而增大。a值增大，说明入渗初期土壤入渗曲线的斜率增大，瞬时入渗率衰减加快，α值增大，说明随着砾石粒径的增加，入渗率衰减速度增加。这与图2中土壤入渗率随入渗时间的变化趋势一致，很好地反映了砾石覆盖对土壤入渗过程的影响。Kostiakov模型的决定系数R2最小为0.921，最大为0.966，其拟合效果最好。在Horton模型的拟合结果中，f1和fc分别代表初始入渗率和稳定入渗率，均随砾石粒径的增大而增大，这与表3的结果一致。由表4可知，f1的模拟值与实际值相差较大，在0.11～3.88 cm/min，但是fc的模拟值和实际值相差较小，仅为0.001～0.042 cm/min。Horton模型的决定系数R2最小为0.929，最大为0.990，拟合结果较好。Philip模型的拟合结果显示，各处理中土壤稳定入渗率A均为负值，且随着砾石粒径的增加而增大；吸渗率S也随砾石粒径的增大而增加，吸渗率在一定程度上能反映土壤初始入渗率的大小，说明渗透早期的土壤入渗能力随覆盖粒径的增大而增大。这与表3的结果一致，S值与土壤实际初始入渗率相差0.76～1.05 cm/min，稳定入渗率A与实际值相差0.002～0.052 cm/min。Philip模型的决定系数R2最小为0.761，最大为0.968，拟合效果较差。综上可知，Horton模型和Philip模型虽然具有一定的物理意义，但在本次土壤水分入渗试验中没有Kostiakov模型的适用性好。

表4 不同粒径砾石覆盖土壤水分入渗模型的拟合结果

4 讨 论

作一维垂向运动的湿润锋运移深度均随着入渗时间延长而增加，且入渗初期其运移速率较快，而后运移速率逐渐减慢趋于稳定状态，这与吉恒莹等[21]的研究结果一致。覆盖砾石后，随着砾石粒径的增大，初始湿润锋的运移距离增大，衰减速度减缓。这是由于随着砾石粒径的增大，覆盖层大孔隙数量增加，因而提高了导水率[16]，但随着入渗深度的增加，覆盖层对入渗的影响逐渐变弱[11]。

与CK相比，砾石覆盖下初始入渗率、稳定入渗率和入渗总量随着砾石粒径增加都呈上升趋势，这与周蓓蓓等[22]的研究结果相似。砾石覆盖显著提高了土壤初始入渗率，且初始入渗率随着砾石粒径的增加而迅速增加，这主要是由于随着砾石粒径的增加，覆盖层的大孔隙数量增多，水流通道好，填满覆盖层孔隙空间所需水分增多。入渗过程中，大孔隙及其传导孔隙是水流的主要通道，土壤中大尺度孔隙的数量和分布直接影响着水分的传输能力和运动状态[23]。随后，土壤入渗率迅速下降，主要是因为入渗初期水分顺着砾石孔隙快速下渗，导致土体快速湿润，土壤团聚体破碎，堵塞了土壤孔隙结构，阻碍了渗水[24]。

最终，土壤入渗率逐渐趋于稳定，达到稳定入渗状态。砾石覆盖提高了稳定入渗率，但稳定入渗率随砾石粒径的增加缓慢增大。导致稳定入渗率增速缓慢的原因有两个：一方面，随着入渗深度的增加，覆盖层对入渗的影响逐渐变小[11]；另一方面，由于砾石自身重力的压实，随着砾石粒径增大，土壤容重增大[25]，随着容重增大，土壤孔隙结构变差，土壤透气性、饱和导水率及导水能力迅速下降[26]，导致稳定入渗率增加缓慢，这与Kostiakov模型的结果一致：稳定入渗率衰减速度随砾石粒径的增大而增加。

砾石覆盖也提高了土壤水分入渗总量，且入渗总量随砾石粒径的增大呈线性增加趋势。出现这种现象的原因是：随着砾石粒径的增大，大孔隙数量增多，水流通道好，土壤的透水性增加。余海龙等[27]指出砾石覆盖能够增加大孔隙，促进水分入渗，加快壤中流的发生，改善土壤水文循环过程。由此可见，砾石覆盖可以改良土壤孔隙结构，增加透水性，提高土壤导水能力，在旱作农业水保措施应用中具有很大优势。

Philip模型的拟合结果中稳定入渗率A均为负值，管瑶[28]和郑健[29]等在研究中也发现了类似的结果。这可能与Philip模型的衰减系数固定为-0.5有关，-0.5的衰减系数限制了Philip模型只能适用于某些特定土壤[28]。土壤入渗模型拟合的结果表明：Kostiakov模型对不同粒径砾石覆盖土壤水分入渗的影响拟合最好；Horton模型的拟合效果较好；Philip模型的拟合效果最差。周蓓蓓[22]和党宏宇[12]等的研究结果也表明Kostiakov模型能够很好地反映砾石覆盖土壤的水分入渗变化过程。本次研究虽然可以使我们了解砾石粒径对土壤水分入渗性能的影响，但是室内土柱模拟试验与研究区实际情况存在一定差异，因此需要在野外建立径流小区进行模拟降雨试验来进一步探讨土壤水分入渗过程。

5 结 论

(1)湿润锋运移距离随时间增长呈幂函数增长，且单位时间内湿润锋运移距离随覆盖砾石粒径的增大而增加。初始入渗率和稳定入渗率均随覆盖砾石粒径的增大呈上升趋势。砾石覆盖粒径对初始入渗率的影响显著，但对稳定入渗率的影响不显著。38.39 mm粒径砾石覆盖的初始入渗率和稳定入渗率最大。

(2)随覆盖砾石粒径的增加入渗总量呈上升趋势，且26.36 mm和38.39 mm粒径砾石覆盖的累积入渗量随时间的变化曲线差异不大，但都明显高于其他处理。Kostiakov入渗模型与Horton和Philip模型相比，Kostiakov入渗模型可以更好地反映砾石覆盖土壤入渗率的变化过程。