基于三维PH曲线的UAV在线路径规划及跟踪控制研究∗

周硙硙

（海军装备部驻南京地区第一军事代表室 南京 210001）

1 引言

随着无人飞行器（Unmanned Aerial Vehicle，UAV）技术的快速发展［1］，UAV的航程、机动性能都得到了大幅提升，使得UAV更加智能化、自动化，使得UAV在目标识别［2］、目标跟踪［3］等方面有着越来越广泛的应用。而日益复杂化的应用环境却对UAV执行任务的能力提出了更高要求。因此，UAV执行任务体系的形成需要对参与执行任务的UAV进行实时在线路径规划，规划的路径需要满足相关性能约束条件，使得执行任务的UAV能够协同工作；同时UAV在执行任务过程中需要准确地跟踪规划的路径，使UAV实际飞行轨迹较小地偏离期望路径。

一些学者对UAV的在线三维路径规划算法进行了研究，文献［4］为保证无人机以最小被发现概率和较小的航程到达目标点，提出一种基于改进蚁群算法的无人机三维路径规划方法；文献［5］针对固定目标规划问题，提出一种动态稀疏A*算法和voronoi图改进算法融合的无人机三维路径规划方法；文献［6］通过栅格化方法对无人机飞行环境进行三维建模，并主要以最短路径为目标，提出了基于改进蚁群算法的无人机三维路径规划方法，但未考虑无人机的性能约束条件；文献［7］综合考虑无人机飞行高度、航迹长度等权重因子，提出了基于改进A*算法的三维无人机路径规划方法，并对规划的路径进行优化，以满足无人机的俯仰角、偏航角、转弯半径等性能约束条件。在路径规划的基础上，设计相关的路径跟踪控制律，从而实现对规划路径的跟踪。文献［8］提出一种基于切换平面的自适应非线性制导方法跟踪规划的三维Dubins路径；文献［9］通过模型参考自适应与动态逆相结合的方法设计路径跟踪控制器，实现对四旋翼无人机三维路径的跟踪控制。

目前，虽然关于UAV路径规划和路径跟踪控制律的设计相对成熟，但是大多数研究都是分开的，没有将路径规划和路径跟踪控制律统筹设计，也很少有利用规划路径特点进行UAV路径跟踪控制律的设计。为此，本文提出一种基于三维五次PH曲线［10～12］的UAV协同路径规划方法，该路径规划算法能够迅速为UAV规划出较优的路径；同时，针对UAV三维PH路径的特点，设计出相应的跟踪控制律，实现对UAV三维PH路径的跟踪控制。

2 基于三维五次PH曲线的UAV路径规划

在三维空间中，当UAV接受任务后，需要在初始位置点 ps(xs,ys,zs)和目标位置点 pf(xf,yf,zf)之间规划出一条满足UAV性能约束的路径r(t)，在ps和 pf处的偏航角和俯仰角分别为(ϕs,ψs)、(ϕf,ψf)，即初始点和目标点处的位姿信息分别为poses(xs,ys,zs,ϕs,ψs)、posef(xf,yf,zf,ϕf,ψf)。那么，UAV路径规划可表述为

2.1 三维五次PH曲线

2.2 基于三维五次PH曲线UAV路径规划

2.3 三维五次PH路径约束条件

3 三维五次PH路径的跟踪控制

基于三维五次PH路径的特点，对UAV三维五次PH路径的跟踪控制采用降维转化的思想，即将UAV的三维PH路径跟踪控制降维转化为UAV二维路径跟踪控制和高度的跟踪控制。在式（3）～（5）和式（7）～（10）的基础上，UAV三维五次PH路径的三个坐标分量都可表示成参数的多项式形式。即

3.1 二维平面路径跟踪控制律设计

基于三维PH路径三个坐标分量可精确已知的特点，采用非线性动态逆控制器设计方法进行路径跟踪控制律设计，可有效降低控制律设计的复杂度。在文献［13］对UAV二维PH路径跟踪控制律设计的基础上，在跟踪UAV三维PH路径时，基于降维跟踪控制思想，相应的二维平面路径跟踪控制律设计为

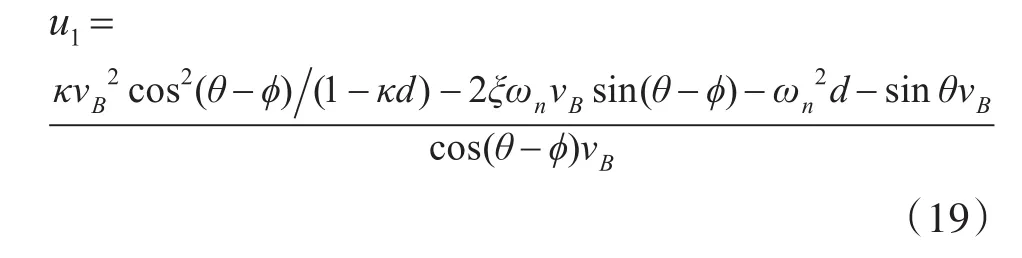
3.2 高度跟踪控制律设计

4 UAV三维五次PH路径规划及跟踪控制仿真

4.1 UAV三维五次PH路径规划仿真

设定UAV的初始位置点Ps和目标位置点Pf分 别 为，Ps和Pf处的两个方向角分别为且最大曲率约束κmax=0.1，最大挠率约束τmax=0.1。相应的Matlab仿真结果如图1和图2所示，图1为UAV三维PH路径，图2为UAV三维PH路径的曲率和挠率曲线。

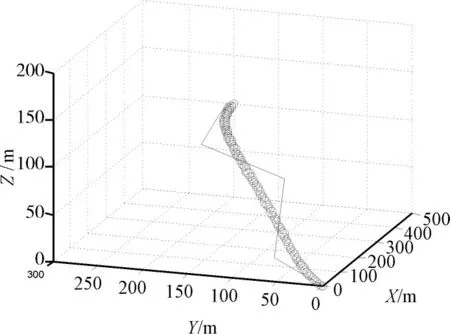
图1 UAV三维PH路径

图2 UAV三维PH路径的曲率和挠率曲线

从图2中可以得出UAV三维PH路径的曲率最大值κmax和挠率最大值τmax分别为0.015、0.075，均小于约束条件值0.1，能够满足UAV可飞行路径的曲率和挠率约束条件。因此，规划出的UAV三维五次PH路径满足要求。

4.2 UAV三维PH路径的跟踪控制仿真

对规划的UAV三维五次PH路径跟踪控制的初始化条件：UAV的速度vB=28m/s，阻尼比ξ=0.707，自然频率ωn=0.12rad/s，UAV路径初始曲率κ0=0，初始跟踪误差d0=0.6m，初始偏航角角θ0=-20°，UAV初始高度h0=0，初始俯仰角ψ0=15°。对UAV三维PH路径的跟踪控制的Matlab仿真结果如图3～6所示。

图3～5分别给出了UAV三维PH路径跟踪的xe误差曲线、ye误差曲线和ze误差曲线；图6为UAV三维五次PH路径跟踪图。从三条误差曲线上可以看出，三维PH路径的跟踪误差被控制在较小值上，可以得出相应的UAV三维PH路径跟踪控制律设计的有效性和可行性，表明基于三维PH曲线规划的UAV路径可跟踪。

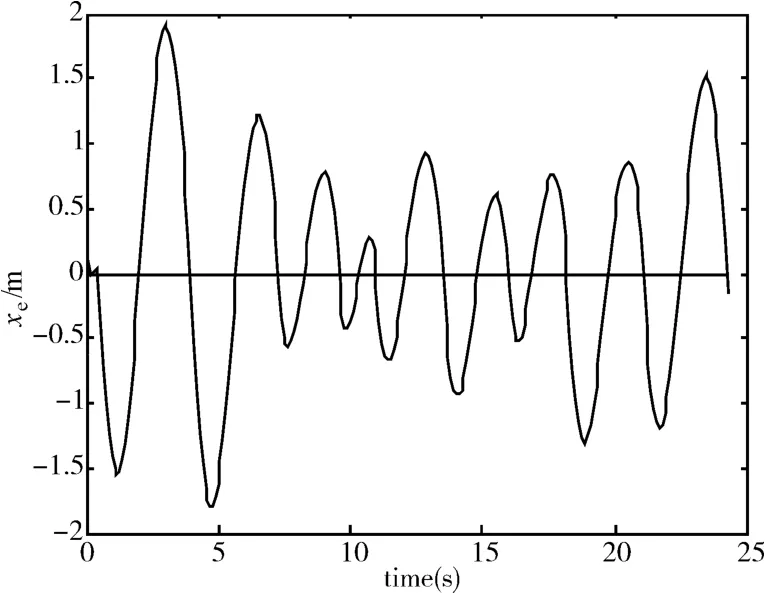
图3 xe误差曲线

图4 ye误差曲线

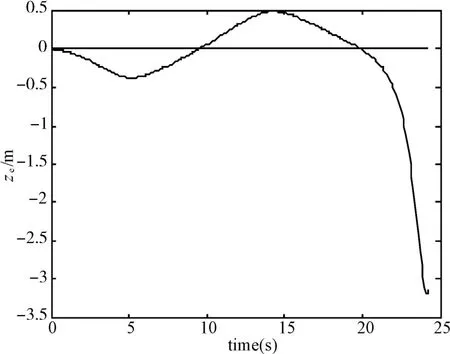
图5 ze误差曲线

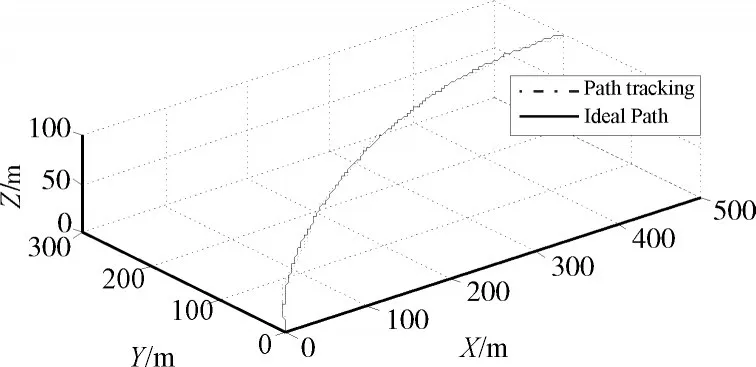
图6 三维五次PH路径跟踪图

5 结语

本文给出一种基于三维五次PH曲线理论的UAV三维路径规划方法，并在路径规划的过程中，考虑UAV的飞行性能约束，使规划出的PH路径安全可飞行；另外针对规划出的UAV三维PH路径参数化等特点，采用降维转化并基于非线性动态逆跟踪控制方法设计出UAV的三维PH路径跟踪控制律。通过Matlab仿真结果验证了提出的UAV三维路径规划和路径跟踪控制律设计方法的有效性和可行性。