基于最优指标组合的企业信用风险预测
周 颖,苏小婷
(大连理工大学 经济管理学院,辽宁 大连 116024)
信用风险预测是指构建企业历史数据与违约状态之间的对应关系,揭示企业的经营发展状况,进而对企业在未来是否会发生违约做出预判。信用风险预测结果不仅能为商业银行提供重要的贷款决策依据,而且能帮助在股票市场、债券上的投资者做出正确的投资决策。
上市公司是中国国民经济发展的关键。据Wind数据库统计,截至2019年前三季度,中国A股上市公司总营收达36 万亿元,同比增长9.54%,占GDP比重突破50%。与此同时,出现财务亏损被证监会特别处理(ST)的上市公司数量也在持续上升,2019 年内共有86 家公司被实施ST,18家公司退市。这一数据也暴露出中国上市公司规模在不断扩张的同时,也存在严重的信用风险问题。因此,建立有效的信用风险预测模型显得极为重要。
建立信用风险预测模型主要涉及两个问题:①信用风险预测模型中指标组合的遴选。与企业信用状态相关联的指标众多,不同的指标组合违约鉴别能力不同,有必要寻找一个违约鉴别能力最强的指标组合,最大限度地区分违约客户和非违约客户。②非平衡样本的处理。上市公司信用数据库中违约客户(ST)的数量远小于非违约客户(非ST)的数量,属于不平衡样本。在利用不平衡样本建模时,会导致模型对违约客户的判对率下降,第2类错误(Type-II error)上升,进而降低模型整体的预测精度。在信用违约预测中第2类错误是指将违约客户误判为非违约客户,若银行错误识别上市公司的信用状况,将贷款发放给违约客户,银行将面临客户无法偿还贷款带来的巨大损失。
本文最优指标组合的遴选与文献[1]中的研究相似。与文献[1]的差别主要有两点:①研究问题不同。文献[1]中研究的是脑电信号的处理,本文研究的是信用风险预测。本文将近邻成分分析引入信用风险领域进行指标组合遴选。②指标重要性的判别标准不同。文献[1]中取指标权重阈值T=τmax(w),τ=0.02作为指标重要性的判别标准,通过剔除指标权重小于阈值T的指标构建指标组合。本文将τ分别设置为0.2,0.02,0.002,…,2×10-8,得到8个不同的指标组合,以指标组合的违约鉴别能力AUC最大反推指标重要性的判别标准τ和最优指标组合。
本文随机欠采样样本配比与文献[2]中的研究相仿。与文献[2]的区别在于,文献[2]中根据经验将违约客户与非违约客户的比例设置为1∶2.5,1∶5,1∶10。本文遍历违约客户与非违约客户的所有可能的样本比例,以G-mean最大反推违约预测模型中两类客户的最佳配比。改变了随机欠采样中主观确定采样比例的不合理做法。
本文的贡献有:
(1)首次将近邻成分分析引入信用风险领域进行指标组合遴选。在近邻成分分析算法中根据违约判别准确率最大得到马氏距离中的指标权重向量,以基于马氏距离的K-近邻的违约判别误差MSE最小为目标,确定最优指标权重向量;给定一个指标权重阈值通过剔除权重小于阈值的指标得到一个指标组合,给定不同的指标权重阈值得到不同的指标组合,以指标组合的违约判别精度AUC 最大反推最优的指标组合。拓展了信用风险领域指标组合遴选的新思路。
(2)利用随机欠采样将违约客户与非违约客户组成不同比例的样本,以基于线性支持向量机的违约预测精度G-mean最大为标准反推违约客户与非违约客户的最佳比例,以确定最优的训练样本。
(3)通过t-m年的指标数据xt-m和t年的企业违约状态yt,利用最优指标组合和最优训练样本建立了支持向量机模型,达到了运用t年的数据xt预测第t+m年企业违约状态yt+m的预测效果。
(4)研究结果表明,本文的违约预测模型的精度高于非线性SVM、LR、DT、KNN 和LDA 等典型的大数据预测模型。
研究表明:每股收益EPS-扣除/稀释、货币供应量M0(亿元)和货币供应量M1(亿元)3个指标对企业未来1~3年的短期违约状态具有关键影响;当日总市值/负债总计、每股EBITDA 和固定资产周转率3个指标对企业未来4~5年的长期违约状态具有关键影响;经营活动产生的现金流量净额/经营活动净收益和审计意见类型2个指标,不论对于企业未来1~3年的短期、还是未来4~5年的长期违约状态,均有关键影响。
1 文献综述
1.1 信用风险预测指标遴选的研究现状
(1)单指标。现有研究大多为单指标遴选,Song等[3]通过fisher判别分析和F值对指标重要性进行排序,删除所有不重要指标,降低了计算成本。Gunduz等[4]提出平衡互信息(BMI)方法检测指标之间的非线性相关关系,进而剔除冗余指标。Lin等[5]在预测P2P 贷款违约时,使用RFE 方法筛选贷款违约行为变量。Gartner等[6]采用信息熵筛选具有鉴别能力的指标。Abbasi等[7]发现,添加行业类指标能显著提高违约预测模型的精度。周颖等[8]通过构造Brown-Mood中位数检验统计量值的方法遴选出违约鉴别力显著的指标。Raghu等[1]通过剔除权重小于阈值的指标构建指标体系。
(2)指标组合。Kozodoi等[9]以利润最大化和指标数量最少为目标函数构建指标体系。葛兴浪等[10]根据企业各类指标的偏相关系数和有序Probit回归系数构建Wald统计量进行指标体系的遴选。Uthayakumar等[11]利用蚁群优化算法构建信用风险预测的最优指标组合。Ping等[12]不断向指标组合中添加指标,通过指标群依赖度的变化量来反映所添加指标的重要性,剔除重要性为零的指标,最终构建信用评价指标体系。石宝峰等[13]通过Logistic回归显著性判别遴选对农户违约状态影响显著的指标,建立了由年龄、非农收入/总收入等13个指标组成的农户小额贷款信用评级指标体系。Jadhav等[14]提出了一种由信息增益和遗传算法相结合的新方法筛选信用评价指标体系。Oreski等[15]基于神经网络和遗传算法筛选出一个包含12个指标的信用评价体系。
单指标遴选的弊端是单个指标违约鉴别能力强,组成的指标组合违约鉴别能力不一定强。现有研究关于指标组合遴选的弊端在于没有以指标组合的违约判别精度最大为标准构建指标体系。本文首次将近邻成分分析(NCA)引入信用风险领域进行指标组合遴选,以指标组合的违约预测精度AUC最大反推最优的指标组合。弥补了现有研究忽略指标组合整体违约鉴别能力的弊端,拓展了信用风险领域指标组合遴选的新思路。
1.2 随机欠采样的研究现状
传统的欠采样方法是随机在多数类样本中抽取一定数量的样本与少数类样本组成比例为1∶1的平衡样本[16-18],但是传统的欠采样方法会丢弃大量数据和重要信息,导致模型过拟合。Louzada等[19]基于Logistic回归研究巴西银行客户的信用风险问题,发现利用随机欠采样获取的平衡样本能显著提高先用评估模型的效果。Jian等[20]对重要违约样本采用过采样方法生成新违约样本,对不重要非违约样本采用欠采样方法剔除非违约样本。Perols等[21]在预测公司欺诈时,将多数类样本划分5个准则层,在每个准则层中随机抽取样本与少数类样本组合,解决了样本的非平衡问题。Dubey等[22]采用K-Medoids欠采样技术对多数类样本聚类,将聚类后的样本与少数类样本组成平衡样本。Paleologo等[23]将非平衡的原始数据集分为若干个子数据集,并通过改变每个子数据集中违约和非违约两类样本的比例进行比较分析。
本文利用随机欠采样技术在非违约客户中抽取样本,将违约客户与非违约客户组成比例为1∶1,1∶2,1∶3,1∶4,1∶5,1∶6的样本,以基于支持向量机的违约预测精度G-mean最大反推违约客户与非违约客户的比例。
1.3 支持向量机预测信用风险的研究现状
不少学者利用支持向量机建立信用风险预测模型,并取得了较高的预测精度[24-26]。Schebesch等[27]对比了线性和非线性支持向量机的违约判别效果,发现非线性支持向量机在实际应用中并没有表现出优势。Kim 等[28]考虑企业财务指标、宏观经济条件和企业管理水平等因素构建支持向量机模型,为韩国中小企业提供信用风险评估模型。Danenas等[29]利用粒子群优化选取最优的线性支持向量机的惩罚系数C,进而构建有效的信用评估模型。Maldonado等[30]将利润函数纳入支持向量机模型,构建智利银行的信用评分系统。
现有研究大多证实了在大型数据库中线性支持向量机的分类效果不会低于非线性支持向量机[31-32]。线性支持向量机能够输出每个指标的权重,具有较好的可解释性,同时,与非线性支持向量机相比,线性支持向量机复杂度更低、运算速度更快。因此,本文选用线性支持向量机作为最终的信用风险预测模型。
2 信用风险预测模型的构建
2.1 最优指标组合的遴选
在原始样本中构建最优指标体系。
2.1.1 基于偏相关性分析的第1次指标筛选
步骤1同一准则层指标相关系数rhg的计算。
设rhg为第h个指标与第g个指标的相关系数,xhj为第h个指标第j个客户的指标数据为第h个指标的平均值,xgj为第g个指标第j个客户的指标数据为第g个指标的平均值。则指标h和指标g的相关系数为[32]
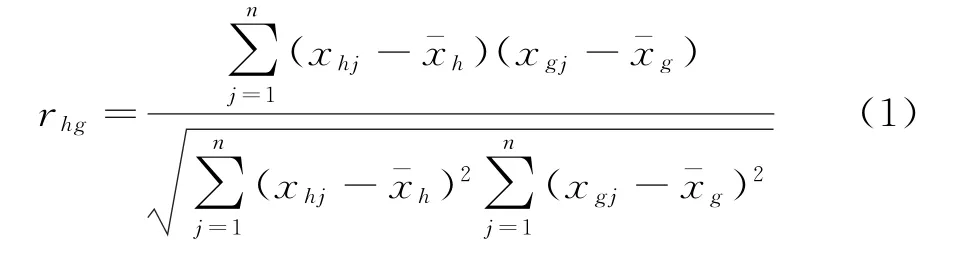
式(1)中,第h个指标与第g个指标的相关系数越大,表明第h个指标与第g个指标的相关性越强;反之,相关性越弱。
设R为指标h与指标g之间的相关系数rhg组成的q×q矩阵,q为准则层内指标的个数。则[33]

R的逆矩阵记为

则指标h与指标g之间的偏相关系数为[32]

式(4)中,指标h与指标g之间的偏相关系数prhg越大,表明指标h与指标g之间的相关性越强;反之,相关性越弱。
步骤2F值的计算。
设Fh为第h个指标的F值为非违约客户中第h个指标的均值为违约客户中第h个指标的均值为全部客户中第h个指标的均值,n(0)为非违约客户的个数,n(1)为违约客户的个数,xhj为第h个指标第j个客户的指标数据,n为客户总数。则[33]

式(5)的经济学含义:式(5)等号右边的分子第1项是第h个指标中非违约客户的均值与所有客户均值的距离,分子第2项是第h个指标中违约客户与所有客户均值的距离。整个分子表示第h个指标中违约客户均值、非违约客户均值与全部客户均值的距离,反映违约客户与非违约客户的差异。分子越大、差异越大,表明第h个指标越能区分企业的违约状态。分母中第1项是第h个指标中非违约客户与非违约客户均值的方差,第2项是第h个指标中违约客户与违约客户均值的方差,整个分母是第h个指标中违约客户内的方差与非违约客户内的方差之和,反映了违约客户、非违约客户各自的离散程度,离散程度越小,表明违约客户、非违约客户内部的指标特征越集中。式(5)中的Fh表示第h个指标的违约鉴别能力,Fh越大,表明指标h的违约鉴别能力越强;反之,越弱。
偏相关性分析是在控制其他变量的线性影响的条件下分析两变量间的线性相关性。避免了当第3个指标同时影响两个指标时,相关性分析不能如实反映两个指标间相关程度的弊端。
步骤3基于偏相关性分析筛选指标的标准。
基于偏相关性分析进行第1次指标筛选有两个标准:①保留具有经济学含义的指标。②在标准①的基础上,计算任意两个指标的偏相关系数,若两个指标的偏相关系数大于0.8,说明这两个指标高度相关,删除F值较小的指标;若两个高度相关的指标均具有较强的经济学含义,则两个指标均保留。
2.1.2 基于近邻成分分析的第2次指标筛选
步骤4定义马氏距离公式。
设dw(xj,xz)为客户j与客户z的距离,s为经过第1次指标筛选后剩余的指标个数,wi为第i个指标的权重,xij为第i个指标第j个客户的指标数据,xiz为第i个指标第z个客户的指标数据。则[1]

式(6)的经济学含义:客户i与客户z的马氏距离越小,表明两个客户的违约状态越可能相同。保证了违约状态相同的客户之间距离较小,违约状态不同的客户之间距离较大。
步骤5客户i与客户z相似概率的确定。
考虑一个随机分类准则:存在一个由n个客户组成的样本,对于其中一个客户j,可以在除自身之外的n-1 个客户中随机选取一个客户作为参考点,以参考点的违约状态判别客户j的违约状态。
设pjz(w)为客户j与客户z的相似概率,由于客户j选择客户z作为参考点,客户j以客户z的违约状态作为客户j自身违约状态的理论标识,故亦可称pjz(w)为客户j选择客户z作为参考点的概率。dw(xj,xz)为客户j、z之间的马氏距离,n为客户总数。则[1]

式(7)中的分子是客户j、z距离的函数,分母是客户j与剩余n-1个客户距离函数的和。式(7)是以距离衡量的概率,当客户j、z之间的距离越小时,违约状态的相似概率越大,客户z被客户j选为参考点的概率Pjz越大。式(7)表示两个客户违约状态相似性的度量。
当客户j的实际违约状态与参考点z的违约状态相同时,则客户j的违约状态通过客户z被判对;当客户j的实际违约状态与参考点z的违约状态不同时,则客户j的违约状态通过客户z被判错。在n个客户中,任意两个客户都可以计算其相似程度,故该相似程度pjz(w)共有n个里边取2的组合,即pjz(w)共有个。对于任意两个客户的指标数据xij和xiz,都可以得到相似度pjz(w)。
步骤6客户j与其他全部n-1个客户相似性的总和。
设pj(w)为客户j的违约状态通过随机分类准则被判对的概率,n为客户总数,pjz(w)为客户j选择客户z作为参考点的概率,yj为客户j实际的违约状态,yz为客户z实际的违约状态。则[1]

式(9)表示当客户j实际的违约状态yj与客户z实际的违约状态yz相同时,yjz=1;否则,yjz=0。式(8)是两个客户相似概率pjz(w)的代数和,即式(8)为第j个客户与其他全部客户相似的概率pj(w)。概率pj(w)越大,则说明第j个客户与其他全部客户的违约状态越一致,此时用其他全部客户的违约状态来判断客户j的违约状态就越合适。式(8)与式(7)不同,式(7)是客户j通过参考点z将自己的违约状态判对的概率,式(8)是客户j通过其他全部客户将自己的违约状态判对的概率pj(w),j=1,2,…,n。
步骤7目标函数F(w)的构建。
设F(w)为目标函数,n为客户总数,pj(w)为客户j通过除自身之外的n-1个客户将自己的违约状态判对的概率。λ为可调节参数,s为第1次指标筛选后剩余的指标个数,wi为第i个指标的权重。则[1]
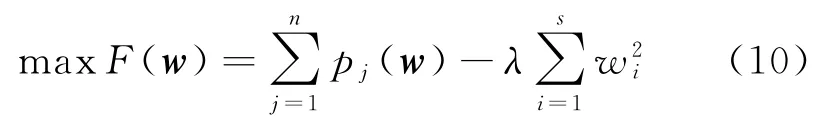
步骤8λ=λ(1)时指标权重向量的确定。
式(10)第1项是式(8)的表达式,而式(8)的表达式是用式(7)计算的,式(7)的距离函数又是由式(6)表达的。由于式(6)是权重向量w的函数,故式(10)第1项是权重向量w的函数,式(10)第2项是w的显函数。因此,式(10)中F(w)是权重向量w的函数。当λ为常数时,通过式(10)最大可以得到一组权重向量。
本文从0 开始,以1/n(n为训练集中样本个数,n=2 397)为步长选取50 个点作为λ的候选值。当λ=λ(1)时,λ(1)为常数,给定一个权重向量w1,1,得到一个目标函数F(w1,1)。给定第l个权重向量,得到第l个目标函数F(w1,l),l=1,2,…,100。比较这100个目标函数值F(w1,l),l=1,2,…,100。F(w)最大所对应的权重向量,即λ=λ(1)时的最优权重向量
步骤9λ=λ(k)时指标权重向量的确定。
在步骤8中已经得到λ=λ(1)时的最优权重向量,重复步骤8,可以得到λ=λ(k),k=2,3,…,50时的最优指标权重向量

步骤10第k个距离表达式d(k)的确定。
将步骤8、9中得到的50个指标权重向量
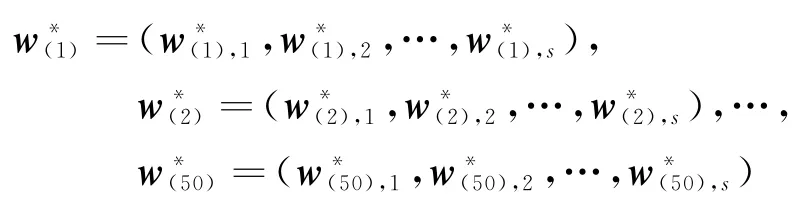
代入式(6),得到50 个距离表达式d(1),d(2),…,d(50),如下式所示:

步骤11第1个客户违约状态的确定。
取步骤10中式(11a)计算第1个客户与任意客户之间的马氏距离,选取与第1个客户距离最小的客户的违约状态作为第1个客户的违约状态的预测值,若与第1个客户距离最近的客户的违约状态是非违约,则第1 个客户的违约状态的预测值=0;若与第1个客户距离最近的客户的违约状态是违约,则。将第1个客户的违约状态预测结果列入步骤12式(12a)等式右端第1列。
同理,取步骤10 中其他49 个表达式(11b)~(11n),运用剩余49个距离表达式得到第1个客户的违约状态预测值,列入下文等式(12a)右端后49列。由此可得到第1个客户在50个距离表达式d(1),d(2),…,d(50)下的违约状态预测值,如下式所示。
步骤12第j个客户违约状态的确定。
仿照步骤11,可以得到第j个客户(j=1,2,…,n)在50 个距离表达式下的违约状态预测值。全部n个客户在50个距离表达式下违约状态的预测值为:

步骤13第1个距离表达式d(1)下违约判别误差MSE(1)的确定。
式(12a)~(12n)可以构成一个n×50的矩阵,将矩阵中第1列n个客户在第1个距离表达式下的违约状态的预测值代入下式,得到违约判别误差为[1]

矩阵中的第1列是在第1个距离表达式d(1)下得到的n个客户的违约状态预测值。因此,MSE(1)就是在第1个距离表达式d(1)下得到的全部客户的违约判别误差。即步骤8中取第1个指标权重向量时得到的全部客户的违约判别误差。
步骤14在第k个距离表达式下违约判别误差MSE(k)的确定。
重复步骤13,依次将式(12)构成的n×50矩阵中的第2列,3列,…,50列代入式(13),得到在第k个距离表达式下的全部客户的违约判别误差MSE(k)(k=1,2,…,50),故可得到由50个MSE 构成的向量MSE=(MSE(1),MSE(2),…,MSE(50))。
步骤15最优指标权重向量w*的确定。
取向量MSE 中最小的一个违约判别误差MSE*=min(MSE),最小的违约判别误差MSE*对应的指标权重向量w*=就是最优的权重向量。
步骤16第1个指标组合D1及指标组合D1的违约预测精度AUC1的确定。
取τ1=0.2,则指标权重的临界点[1]T1=τ1max(w*)=0.2max(w*),T1为常数,对比T1和步骤15中得到的每个指标的权重权重大于临界点T1的重要指标即构成了一个指标组合D1。将训练集中n个客户对应指标组合D1中的指标数据xij和实际违约状态yj代入下文式(14)~(16),构建线性支持向量机模型。对训练集上客户的违约状态进行判别,得到客户的违约状态预测值,根据客户违约状态的实际值yj和预测值计算线性支持向量机的违约判别精度AUC1。
步骤17其他指标组合及违约预测精度的确定。
依次 取τ2=0.02,τ3=0.002,…,τ8=2×10-8(见表7),则指标权重的临界点

重复步骤16,得到另外7 个指标组合D2,D3,…,D8及7 个指标组合的违约预测精度AUC2,AUC3,…,AUC8。
步骤18最优指标组合D*的确定。
比较步骤16、17中得到的8个AUC,AUC 最大所对应的指标组合即为最优的指标组合D*。以下文t-1年实证为例,AUC 最大对应的最优指标组合由表8前22行指标构成。
本文利用近邻成分分析筛选指标与文献[1]主要存在两点差别:①研究问题不同。文献[1]中研究的是脑电信号的处理,本文研究的是信用风险预测。本文首次将近邻成分分析引入信用风险领域进行指标组合遴选。②指标重要性的判别标准不同。文献[1]中取指标权重阈值T=τmax(w),τ=0.02作为指标重要性的判别标准,通过剔除指标权重小于阈值T的指标构建指标组合。本文将τ分别设置为0.2,0.02,0.002,…,2×10-8,得到8 个不同的指标组合,以指标组合的违约鉴别能力AUC 最大反推指标重要性的判别标准τ和最优指标组合。保证了指标组合整体的违约鉴别能力。
步骤4~8最优指标组合遴选的特色在于:首次将近邻成分分析引入信用风险领域进行指标组合遴选,在近邻成分分析算法中根据违约判别准确率最大得到马氏距离中的指标权重向量,以基于马氏距离的K-近邻的违约判别误差MSE 最小为目标,确定最优指标权重向量;给定一个指标权重阈值、并通过剔除权重小于阈值的指标得到一个指标组合,给定不同的指标权重阈值得到不同的指标组合,以指标组合的违约判别精度AUC 最大反推最优的指标组合。拓展了信用风险领域指标组合遴选的新思路。
2.2 违约预测模型中两类客户配比的选择
本文在指标组合遴选中未对样本比例进行处理,样本比例的处理仅在指标组合遴选后建立违约预测模型时用到。
中国上市公司中违约样本数量与非违约样本数量的原始比例大概为1∶6.2,属于非平衡样本。本文以随机欠采样为基础处理非平衡样本。通常随机欠采样是从非违约客户中随机抽取与违约客户数量相同的非违约客户,使之构成1∶1的平衡样本。对非违约客户进行多次采样,将全部违约客户与采样后的非违约客户分别组成比例为1∶1、1∶2、1∶3、1∶4、1∶5和1∶6共6组采样后的样本。
以下文实证数据为例,将训练集中全部333个违约客户与训练集中随机抽取的333个非违约客户组成样本比例为1∶1的训练子样本。同理,将训练样本中全部333个违约客户分别与在训练样本中随机抽取的666,999,1 332,1 665,1 998个非违约客户组成样本比例为1∶2,1∶3,1∶4,1∶5,1∶6的训练子样本Q1,Q2,Q3,Q4,Q5,Q6。6组训练样本如表1所示。

表1 违约客户与非违约客户构成的6组训练样本
根据Q1,Q2,…,Q6共6组训练样本,采用3.3节的线性支持向量机模型建立6个违约预测模型,得到6个违约预测精度G-mean,以G-mean最大反推违约预测模型中两类客户的最佳配比。
本文处理非平衡样本与现有研究的差别在于:现有研究[34,35]将非违约公司与违约公司的比率设定为1∶1研究企业信用风险。He等[2]根据经验将违约客户与非违约客户的比例设置为1∶2.5,1∶5,1∶10。本文遍历违约客户与非违约客户所有可能的样本比例,以G-mean最大反推违约预测模型中两类客户的最佳配比。改变了随机欠采样中主观确定采样比例的不合理做法。
本文对非平衡样本随机欠采样的处理特色是将违约客户与非违约客户组成不同比例的样本,以基于线性支持向量机的违约预测精度G-mean最大为标准反推违约客户与非违约客户的最佳比例,以确定最优的训练样本。改变了现有研究中主观设置欠采样比例的做法。
2.3 基于线性支持向量机构建信用风险预测模型
有研究表明,线性支持向量机针对大型数据集(样本数量大于等于2 000)具有较好的分类效果,而非线性支持向量机针对大型数据集的分类效果并不佳[35]。本文基于3 425家上市公司数据构建信用风险预测模型,选取线性支持向量机作为最终的信用判别模型。
设w为指标的权重向量,yj为客户j的实际违约状态(-1表示非违约,1表示违约),xj为客户j的指标向量,对应步骤18中遴选出的最优指标组合,即表8中前22行指标构成的指标向量,b为截距,n为客户总数。则支持向量机的目标函数为[35]:

通过引入拉格朗日乘子α,求解出指标权重向量w*和截距b*。

式(14)~(16)的经济学含义:两类客户到超平面的距离之和为是两类客户之间距离的倒数,w越小,两类客户之间距离越大,违约判别精度越高。
本文构建的支持向量机与文献[29,34]相比有两个差别:①使用的指标组合是以违约判别误差最小遴选出的最优指标组合;②构建线性支持向量机所使用的最佳样本配比是根据违约判别精度Gmean最大反推得到的。
本文构建的线性支持向量机有两个特色:①最优指标组合遴选的特色。在近邻成分分析算法中根据违约判别准确率最大得到马氏距离中的指标权重向量,以基于马氏距离的K-近邻的违约判别误差MSE最小为目标,确定最优指标权重向量;给定一个指标权重阈值通过剔除权重小于阈值的指标得到一个指标组合,给定不同的指标权重阈值得到不同的指标组合,以指标组合的违约判别精度AUC 最大反推最优的指标组合。②最佳样本配比的特色。利用随机欠采样将违约客户与非违约客户组成不同比例的样本,以基于线性支持向量机的违约预测精度G-mean最大为标准,反推违约客户与非违约客户的最佳配比。
2.4 对比模型精度的检验标准
通常混淆矩阵可以用来作为违约判别模型分类效果的评价基础。混淆矩阵如表2所示。

表2 违约判别混淆矩阵
采用精确度(Acc)、第1类错误(Type I error)、第2类错误(Type II error)、几何平均值(G-mean)以及AUC 作为信用风险预测模型的精度检验标准[36]。各检验标准的定义及计算公式如下式所示。
准确率(Acc)是指违约客户被判为违约的数量与非违约客户被判为非违约的数量之和占总客户数的比,即

第1类错误(Type I error)是指非违约客户被判为违约的数量占非违约客户总数的比,即

第2类错误(Type II error)是指违约客户被判为非违约的数量占违约客户总数的比,即
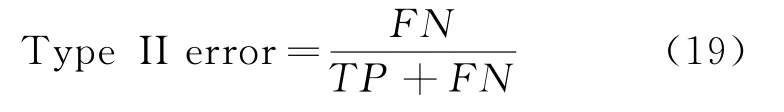
在利用不平衡数据进行客户违约状态判别时,通常利用G-mean作为评价判别模型好坏的标准,因为G-mean同时考虑了违约客户和非违约客户的判对率,即

违约客户判对率(TPR)亦称召回率(recall)、灵敏度(sensitivity),是指违约客户被判为违约的数量占违约客户总数的比,即
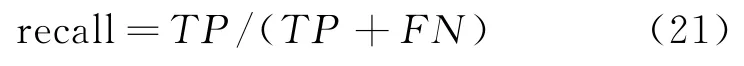
非违约客户判对率(TNR)亦称特异度(specificity),是指非违约客户被判为非违约的数量占非违约客户总数的比,即

以(1-特异度)为横坐标,灵敏度为纵坐标,得到曲线ROC,ROC曲线与坐标轴围成的面积即为AUC。通常利用AUC的值作为评价分类模型精度的标准,AUC的值越大,违约预测模型的预测效果越好[35]。
3 实证研究
3.1 样本数据
3.1.1 原始样本的来源
(1)指标海选。由于企业信用状况涉及多方面因素,为使指标体系能全面反映企业现阶段的信用状况,从企业的财务状况、非财务状况以及宏观经济环境等方面海选出614个指标,其中包含342个公司财务指标[38],119个非财务指标[39-40],147个宏观经济指标和6个与货币发行量相关的指标[41-42]。初始指标体系涵盖企业偿债能力、盈利能力、营运能力、成长能力、非财务因素、企业高管基本情况、企业基本信用情况、商业信誉、社会责任以及外部宏观因素等多个准则层。表3列举了本文海选出的主要指标。
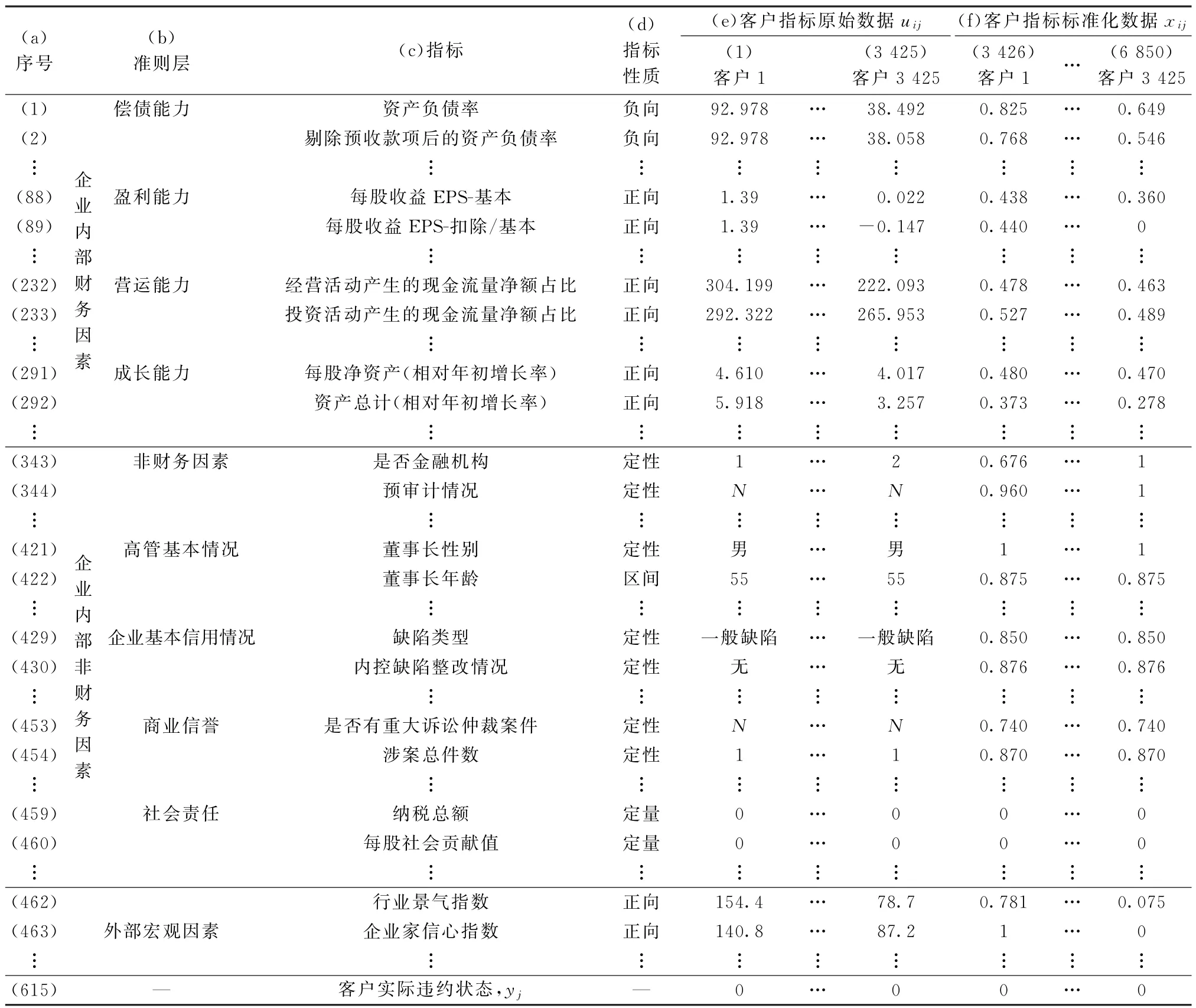
表3 上市公司信用风险预测初始指标体系
(2)原始样本数据。以中国上市公司为研究对象,选取2000~2018年期间3 425家上市公司数据作为样本,构建企业违约判别模型。所使用的数据来自Wind数据库、国泰安数据库、国家统计局。若上市公司连续两年出现亏损,该公司就会被中国证监会特别处理(Specially Treated,ST)。以企业是否被标ST 为标准,将上市公司分为违约客户和非违约客户。其中,违约客户476 家,非违约客户2 949家。3 425家上市公司的原始数据uij列于表3第(1)~(3 425)列。
利用客户第t-m(m=1,2,3,4,5)年的指标数据xij和第t年的违约状态yj进行建模。对于违约客户,将客户违约当年作为第t年。对于非违约客户,在不重复的情况下每年选取一定数量的客户,将客户对应的年份作为第t年。
3.1.2 指标数据标准化处理 标准化的目的是将指标数据转化为[0,1]区间内的数值,消除数据的单位限制,便于不同单位间的数据进行加权。采用Chi等[43]的方法对原始指标uij进行标准化处理。将客户标准化后的指标数据xij列于表3第(f)列。指标的标准化处理不是本文的主要工作,故不再赘述。
3.1.3 训练集与测试集划分 将样本按照7∶3的方式划分训练集与测试集,如表4所示。
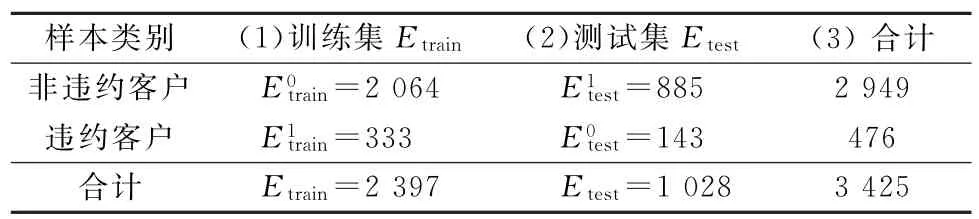
表4 样本划分
从非违约样本与违约样本中分别抽取70%的样本组成训练集Etrain,即训练集中包含2 397个客户,其中,违约客户=333 个,非违约客户2 064个。非违约样本与违约样本中分别剩余的30%样本组成测试集Etest,即测试集中包含1 028个客户,其中,违约客户=885 个,非违约客户=143个。
(1)指标遴选时使用的样本。在指标遴选过程中仅使用表4列(1)的训练样本Etrain,不使用列(2)的测试样本Etest。
(2)构建模型时使用的样本。在表4列(1)训练样本中,采用表1中6个不同的比例,运用表3列(f)的数据xij和yj,建立式(14)~(16)的支持向量机模型。
(3)测试样本。上文(2)使用6个样本建模,由此建立了6个预测模型。对于6个模型中的每一个模型,都采用表4列(2)的测试样本、表3列(f)的数据xij进行判别,由此得到理论判别状态。通过将和测试样本的实际违约状态yj进行对比,得到了表2混淆矩阵的全部统计频数,将统计频数对应代入式(20),可以得到违约预测精度G-mean,如表11列(8)所示。
3.2 最优指标组合的确定
3.2.1 第1次指标筛选 依照步骤1~3 进行基于偏相关性分析的第1 次指标遴选。将表4 列(1)定义的训练集样本Etrain对应表3列(f)前614行的指标数据xij代入式(1)~(4)计算任意两个客户间的偏相关系数,代入式(5)计算每个指标的F统计量。挑选出具备经济学含义且偏相关系数大于0.8的指标对,删除指标对中经济学含义不明显或F统计量较小的指标。由此,614 个指标经过第1 次指标筛选剩余259 个指标,将剩余的259个指标列于表5 列(c)前259 行。表5 列(d)为训练集Etrain中2 397个客户的指标数据xij,列(e)为测试集Etest中1 028个客户的指标数据xij。
3.2.2 第2次指标筛选 在第1次指标筛选剩余的259个指标的基础上进行第2次指标筛选,目的是遴选出违约预测能力最强的指标组合。以t-1年为例(t-m年的其他年份类推,下同),依照步骤4~18,具体说明最优指标组合的遴选过程。
步骤19λ取值范围的确定。
如表4列(1)第3 行所示,训练集中样本总数n=2 397,则1/n=1/2 397=0.000 417。根据步骤8,从0开始,以0.000 417为步长,取50个点作为λ的候选值,如表6列(2)所示。
步骤20任意两个客户间距离表达式的确定。
将表5列(1)前259行数据xi1和列(d)剩余的2 396 列中任意一列的前259 行数据xiz代入式(6),得到第1个客户与其他2 396个客户关于权重w的距离表达式dw(x1,xz),其中,z=2,3,…,2 397,共计2 396个距离表达式。同理,对于表5列(d)中任意一个客户j,均可求出其与其他2 396个客户的2 396个距离表达式dw(xj,xz)。由于表5列(d)中有2 397个客户,故依照上述方法可以得到2 397×2 396=5 743 212个距离表达式。由于dw(xj,xz)=dw(xz,xj),故有2 871 606个距离表达式。
步骤21任意两个客户间相似度pjz(w)的确定。
将步骤20中得到的第1 个客户与其他2 396个客户的2 396个距离表达式dw(x1,xz),z=2,3,…,2 397代入式(7),得到客户1与其他2 396个客户关于权重w的相似概率函数p1z(w),共计2 396个相似概率函数。同理,对于表5列(d)中任意一个客户j,j=1,2,…,2 397,均可求出其与其他2 396个客户关于权重w的2 396 个相似概率函数pjz(w)。
步骤22客户j与其余2 396个客户相似度总和pj(w)的确定。
将步骤21中得到的2 396个p1z(w)代入式(8),同时将y1z也代入式(8),得到客户1与其余2 396个客户相似概率的总和p1(w)。关于y1z的取值如下:对比表5列(d)最后一行中第1个客户与其他客户的实际违约状态y1和yz,若客户1与客户z实际违约状态同时为0或同时为1,则y1z=1;否则,y1z=0。同理,对于表5列(d)中任意一个客户j,均可求出其与其他2 396个客户相似概率的总和pj(w)。
步骤23权重向量的确定。
将步骤22中的Pj(w)代入式(10),同时将表6第1行第(2)列数据λ=0也代入式(10)。由此,得到一个仅由w组成的目标函数F(w),以F(w)最大为目标,计算得到=(0.003 12,…,0.001 79),列于表6第1行第(3)列。
步骤24权重向量的确定。
重复步骤23,依次取表6第(2)列第2~50行的可调节参数λk,得到对应行的权重向量其中,k=2,3,…,50,列于表6第(3)列的对应行。
步骤25两个客户间距离的确定。
将表5列(d)中任意两个客户的前259行数据xij、xiz以及表6 中第1 行第(3)列数据(0.003 12,…,0.001 79)代入式(11a),得到当w==(0.003 12,…,0.001 79)时任意两个客户之间的距离同理,依次取表6第(3)列第2~50行的数据代入式(11b)~(11n),将表5列(d)中任意两个客户的前259行数据xij和xiz也代入式(11b)~(11n),得到当w=时任意两个客户之间的距离(xj,xz),其中,k=2,3,…,50。

表5 基于相关性分析的指标筛选结果
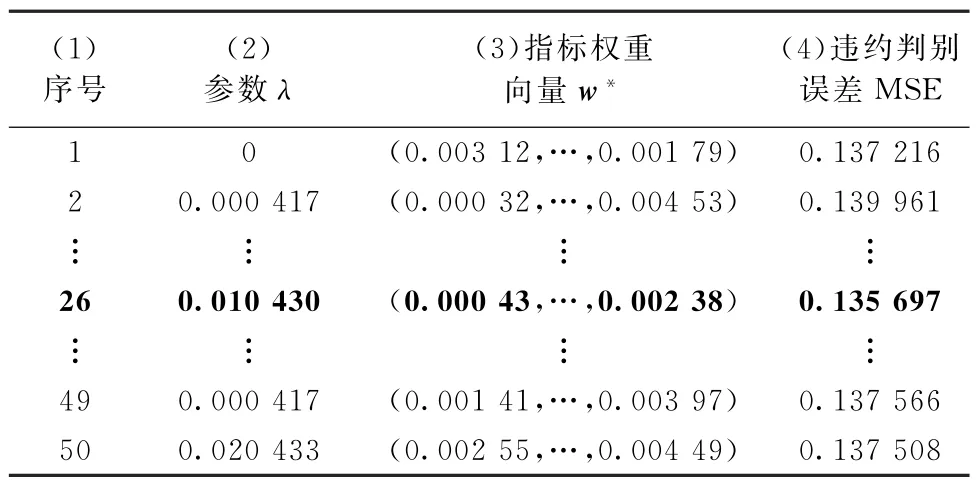
表6 不同λ 下的违约判别误差
步骤26第1个客户违约状态的确定。
取步骤25中第1个客户在第1个距离表达式下与其余2 396个客户的距离(x1,xz),其中,z=2,3,…,2 396,共计2 396 个距离。比较这2 396个距离,选取最小距离所对应的客户。若与第1个客户距离最小的客户的违约状态为0,则第1个客户的违约状态的预测值=0;若与第1个客户距离最小的客户的违约状态为1,则第1个客户的违约状态的预测值=1。由此,得到第1个客户在第1个距离表达式下的违约状态,列于下式矩阵A的第1行第1列。同理,取步骤25中第1个客户在第k(k=2,3,…,50)个表达式下与其余2 396个客户的距离,得到第1个客户在第k个距离表达式下的违约状态列于下式矩阵A的第1行后49列。
步骤27第j个客户违约状态的确定。
仿照步骤26,得到第j个客户在第k个距离表达式下的违约状态,列于下式矩阵A第j行第k列,即

步骤28第1个距离表达式d(1)下违约判别误差MSE(1)的确定。
将式(23)中矩阵A第1列代入式(13),同时将表5 列(d)最后一行也代入式(13),得到违约判别误差MSE(1)=0.137 216,列于表6第(4)列第1行。
步骤29第k个距离表达式下违约判别误差MSE(k)的确定。
重复步骤28,依次取式(23)中矩阵A第2~50列,得到违约判别误差MSE(2),…,MSE(50),列于表6第(4)列第2~50行。
步骤30最优指标权重向量w*的确定。
比较表6第(4)列中50个违约判别误差MSE,选取最小的违约判别误差min MSE=0.067 167及其对应的最优指标权重向量w*=(0.000 43,…,0.002 38)。
步骤31指标权重阈值的确定。
取指标重要性的判别标准τ1=0.2,τ2=0.02,…,τ8=2×10-8,如表7第(2)列所示。

表7 不同临界点τ 下的违约预测精度
步骤32第1个指标组合D1及指标组合D1的违约预测精度AUC1的确定。
取表7 第(2)列第1 行数据τ1=0.2 和步骤30中得到的w*=(0.000 43,…,0.002 38),则指标权重阈值T1=τ1max(w)=0.001 48。将w*中每个指标的权重与T1=0.001 48比较,保留指标权重大于0.001 48的指标。这些指标即构成了一个指标组合D1。将表4第(1)列的训练样本对应指标组合D1中的xij和表5第(d)列最后一行的yj代入式(14)、(15),得到线性支持向量机中的指标权重向量w*和截距b*,再将w*和b*代入式(16)构建SVM1。将表4第(1)列的训练样本对应指标组合D1中的xij代入SVM1,得到客户的违约状态预测值,根据客户违约状态的实际值y与预测值计算得到线性支持向量机的违约判别精度AUC1=0.982 8,列于表7 第1 行第(3)列。
步骤33第q个指标组合Dq及指标组合Dq的违约预测精度AUCq的确定。
重复步骤32,依次取表7第(2)列第2~8行数据,并得到对应行的违约预测精度,列于表7第(3)列第2~8行。
步骤34最优指标组合D*的确定。
比较表7第(3)列8个数值,τ=2×10-7对应的AUC最大,为0.991 9,故τ=2×10-7对应的指标组合为t-1年最优的指标组合。t-1年最优的指标组合列于表8前22行。

表8 t-1年上市公司信用评价指标体系
同理,根据t-1年信用风险预测指标体系的构建流程,分别建立t-2年,t-3年,t-4年,t-5年的信用风险预测指标体系。其他年份下的最优指标组合遴选结果详见附录。
表9汇总了t-m(m=1,2,3,4,5)年最优指标组合中的指标,并统计了各个指标被选入最优指标组合的次数。
根据表9 列(3)可知,每股收益EPS-扣除/稀释、货币供应量M0(亿元)和货币供应量M1(亿元)3个指标存在于t-1,t-2,t-3年的最优指标组合中,说明这3个指标对企业未来1~3年的短期违约状态具有关键影响;当日总市值/负债总计、每股EBITDA 和固定资产周转率3个指标存在于t-4,t-5年的最优指标组合中,说明这3个指标对企业未来4~5年的长期违约状态具有关键影响;同时,经营活动产生的现金流量净额/经营活动净收益和审计意见类型2个指标存在于t-m(m=1,2,3,4,5)年的最优指标组合中,说明这2个指标不论对于企业未来1~3年的短期、还是未来4~5年的长期违约状态,均有关键影响。

表9 t-m(m=1,2,3,4,5)年最优指标组合汇总
由此可以得出结论:每股收益EPS-扣除/稀释、货币供应量M0(亿元)和货币供应量M1(亿元)3个指标对企业未来1~3年的短期违约状态具有关键影响;当日总市值/负债总计、每股EBITDA 和固定资产周转率3个指标对企业未来4~5年的长期违约状态具有关键影响;经营活动产生的现金流量净额/经营活动净收益和审计意见类型2个指标,不论对于企业未来1~3年的短期、还是未来4~5年的长期违约状态,均有关键影响。
3.3 基于不同比例的样本构成
在训练样本Etrain中随机抽取333个非违约客户,将Etrain中全部333个违约客户与抽取的333个非违约客户组成比例为1∶1的训练子样本Q1。依照上述方法,将Etrain中全部333个违约客户分别与在Etrain中随机抽取的666,999,1 332,1 665,1 998个非违约客户组成比例为1∶2,1∶3,1∶4,1∶5,1∶6的训练子样本Q2,Q3,Q4,Q5,Q6(见表1)。通过样本Etrain,Q1,Q2,…,Q6构建7 个线性支持向量机,以线性支持向量机的G-mean最大反推违约客户与非违约客户的最佳样本比。以训练样本Q2为例,具体样本构成如表10所示。
3.4 最佳线性支持向量机的确定
3.4.1 线性支持向量机的构建 以预测期限m=1为例,利用训练样本Q2构建样本比为1∶2的线性支持向量机。将表10中前22行的指标数据xij,第23行客户的实际违约状态yj代入式(14)、(15),估计得到线性支持向量机的指标权重向量w1,1:2和截距b1,1:2。将w1,1:2和b1,1:2代入式(16),得到预测期限m=1,违约与非违约客户的样本比为1∶2的线性支持向量机模型,如式(24)所示。同理,利用训练样本Q1,Q3,Q4,Q5,Q6,Etrain可以构建预测期限为m=1,违约与非违约客户的样本比为1∶1、1∶3、1∶4、1∶5、1∶6和原始比例的违约预测模型。当m=2,3,4,5时,利用训练样本Q1,Q3,Q4,Q5,Q6,Etrain构建违约与非违约客户样本比为1∶1、1∶2、1∶3、1∶4、1∶5、1∶6和原始比例的违约预测模型。共计35个线性支持向量机模型。

表10 t-1年训练样本Q 2
3.4.2 最佳样本比的确定 将表4列(2)的测试样本Etest对应表3列(f)的训练样本的数据xij代入t-1年构建的7个线性支持向量机,得到测试样本中客户违约状态的预测值,将与实际值y对比,得到t-1年不同样本比例下的违约预测精度,如表11第1~7行所示。同理,得到t-m(m=2,3,4,5)年下构建的其他28个模型的违约判别精度,如表11第8~35行所示。
本文以G-mean衡量违约预测模型的精度,因为G-mean同时考虑了违约客户和非违约客户的判对率。比较表11结果可以发现:当预测期限m=1,2,5,样本比为1∶2时,G-mean为最大值;当m=3,4,样本比为1∶1时,G-mean为最大值。由上述结果可以确定:当m=1,2,5时,违约客户与非违约客户的最佳样本比例为1∶2;当m=3,4时,违约客户与非违约客户的最佳样本比例为1∶1。通过表11还可以看出,在每一预测期限下,基于最佳样本比构建的模型的第2 类错误(Type-II error)、召回率(recall)、G-mean以及AUC 均优于基于原始样本构建的模型。

表11 基于不同样本比例的预测结果
由此可得结论:利用违约样本与非违约样本的最佳样本比能够提高预测模型的预测能力。
根据不同年份下的最佳样本比,可以确定不同年份下的最佳违约预测模型。t-m(m=1,2,3,4,5)年的最佳违约预测模型如式(24)~(28)所示。

式(24)~(28)中,sgn表示若方括号内的数值计算结果大于0,则sgn[]取“1”,表示第j个客户违约;若小于0,则sgn[]取“-1”,表示第j个客户非违约;若等于0,则sgn[]取“0”,此时不能识别第j个客户的违约状态。
3.5 模型精度的对比
3.5.1 指标筛选方法的对比 将本文的指标筛选方法与蓝本文献[1]中的指标筛选方法进行对比。蓝本文献将指标重要性的判别标准τ设置为0.02,本文将τ分别设置为0.2,0.02,0.002,…,2×10-8,得到8个不同的指标组合,以指标组合在训练集中的违约鉴别能力AUC 最大反推指标重要性的判别标准τ和最优指标组合。
本文指标筛选方法记为NCA1,蓝本文献指标筛选方法记为NCA2。将对比结果列于表12。
由表12可以看出,在每一个预测期限下,利用本文的指标筛选方法(NCA1)构建最优指标组合,线性支持向量机的第2 类错误(Type-II error)、召回率(recall)、G-mean以及AUC 均为最优值。

表12 指标筛选方法的精度对比
由此可得结论:基于最优的指标权重阈值遴选指标组合能够提高指标组合的违约鉴别能力。在t-m(m=1,2,3,4,5)年,基于近邻成分分析构建的指标体系,使得模型预测精度AUC 达到0.9以上,说明本文将近邻成分分析(NCA)方法引入信用风险领域进行指标组合遴选是有效的。
3.5.2 信用风险预测模型的对比 将本文构建的违约预测模型 (Neighborhood Component Analysis-Undersampling-Support Vector Machine,NCA-US-SVM)与其他经典违约预测模型如非线性支持向量机[44]、逻辑回归(LR)[45]、决策树(DT)[44]、K-近 邻(KNN)[46]以及线性判别(LDA)[47]进行对比,结果列于表13。
通过表13可以看出,不同的预测期限下,本文构建的NCA-US-SVM 模型的第2类错误(Type-II error)、召回率(recall)均优于其他模型。当m=2,3,4,5时,NCA-US-SVM 模型的G-mean优于其他模型;当m=1,2,3,4 时,NCA-US-SVM 模型的AUC优于其他模型。总体而言,本文构建的违约预测模型的违约预测能力优于其他经典模型。
4 结论
本文主要结论如下:
(1)在邻近成分分析的马氏距离中,以违约判别误差最小确定马氏距离中的指标权重向量,通过淘汰权重低于临界点的指标,得到一组AUC 最大的最优指标组合。通过对比不同预测期限下的最优指标组合可知:每股收益EPS-扣除/稀释、货币供应量M0(亿元)和货币供应量M1(亿元)3个指标对企业未来1~3年的短期违约状态具有关键影响;当日总市值/负债总计、每股EBITDA 和固定资产周转率3个指标对企业未来4~5年的长期违约状态具有关键影响;经营活动产生的现金流量净额/经营活动净收益和审计意见类型2个指标,不论对于企业未来1~3年的短期、还是未来4~5年的长期违约状态,均有关键影响。
(2)利用随机欠采样方法将两类客户组成不同比例的样本,以G-mean最大为标准得到不同年份下线性支持向量机的最佳样本配比。以本文实证为例:对于中国上市公司,t-1,t-2,t-3年违约客户与非违约客户的最佳样本比为1∶2;t-4,t-5年违约客户与非违约客户的最佳样本比为1∶1。
本文主要创新点:
(1)在近邻成分分析算法中根据违约判别准确率最大得到马氏距离中的指标权重向量,以基于马氏距离的K-近邻的违约判别误差MSE 最小为目标,确定最优指标权重向量;给定一个指标权重阈值、并通过剔除权重小于阈值的指标得到一个指标组合,给定不同的指标权重阈值得到不同的指标组合,以指标组合的违约判别精度AUC 最大反推最优的指标组合。拓展了信用风险领域指标组合遴选的新思路。
(2)利用随机欠采样将违约客户与非违约客户组成不同比例的样本,以基于线性支持向量机的违约预测精度G-mean最大为标准反推违约客户与非违约客户的最佳比例,以确定最优的训练样本。
(3)通过t-m年的指标数据xt-m和t年的企业违约状态yt,利用最优指标组合和最优训练样本建立了支持向量机模型,达到了运用t年的数据xt预测第t+m年企业违约状态yt+m的预测效果。
(4)本文的违约预测模型的精度高于非线性SVM、LR、DT、KNN 和LDA 等典型的大数据预测模型。

附表1 t-2年上市公司信用评价指标体系

附表2 t-3年上市公司信用评价指标体系

附表3 t-4年上市公司信用评价指标体系

附表4 t-5年上市公司信用评价指标体系

