GaInP2 LEO 空间太阳电池功率衰减估计

李 强，赵 岩，曹继宏，李会锋，王 超

（1.航天器在轨故障诊断与维修重点实验室，西安 710043；2.宇航动力学国家重点实验室，西安 710043）

太阳电池在轨工作过程中，受空间环境的影响，一般会出现功率缓慢衰减[1]。太阳电池功率衰减可能会对负载的能源预算和平衡产生一定的影响，严重时可能会造成能源短缺甚至任务失败。因此，在轨管理中，需要对太阳电池功率衰减给予足够关注，而在卫星的长寿命应用场合下则更是如此。

太阳电池阵的衰减特性目前多采用地面测试与空间验证等方法进行研究和考察[2]，重点关注空间高能粒子辐射、紫外、原子氧和真空等因素[3]对电池、盖片以及黏胶等物质的复杂影响。文献[4]介绍了Spectrolab 公司最新研发的抗辐照空间太阳电池，初始转换效率高于32%，适于高、中、低不同轨道环境下的应用；文献[5]报道了国产四结砷化镓太阳电池研制进展，地面测试所得转换效率在34%以上，但长期在轨应用与空间辐照下的衰减性能还有待进一步验证；文献[6]检验了紫外辐照下的透明硅胶对太阳电池阵功率衰减的影响，认为其在衰减中的比重要高于传统认定的2%，且环境温度较高时更甚；文献[7]研究了三结砷化镓电池GaInP/GaIn As/Ge 的抗辐照性能，指出GaInAs 与Ge 子电池对带电粒子辐射更为敏感；文献[8]进行了低地球轨道环境下的太阳电池盖片的静电放电测试，结果表明，随着原子氧侵蚀加剧，静电放电阈值随之降低；文献[9]针对传统太阳电池功率衰减模型计算过程复杂的问题，提出一种轨道优化下的新预测方法，适宜于连续小推力下的轨道转移任务场合；文献[10]利用聚类方法对卫星入轨早期近一年的遥测数据进行太阳电池阵功率衰减估计，年衰减率约为1.45%，算法效果较好。以上工作基本针对硅、砷化镓类型太阳电池功率衰减进行，关于GaInP2太阳电池的在轨衰减情况，报道资料则相对较少。

本文以GaInP2太阳电池为对象，对其在轨功率衰减进行估计与预测，用于在轨卫星长期管理与测控中的遥测诊断辅助和器件健康状态评估[11]等方面。

1 太阳电池电流与温度

某近地卫星运行在太阳同步轨道，降交点地方时在AM 06∶30 附近，初始轨道高度约490 km（近圆轨道），整星采用三轴零动量控制。太阳电池阵固定安装在卫星本体的±X 两侧（无驱动），在轨运行时，电池阵法线方向与轨道法线方向平行。

卫星入轨以来的倾角、降交点地方时、光照角与日地距离因子变化如图1 所示。

图1 轨道参数变化Fig.1 Variations in orbital parameters

图1 中，定义光照角为电池阵法线与日地矢量的夹角，日地距离因子为日地距离与平均日地距离的比值（平均日地距离取为1.496×109km）。

光照角具有年周期、双峰值的特征。夏至与冬至前后有极大值，且夏至前后的光照角最大；春分与秋分附近有极小值，2015 年春分前后的光照角为最小值。以2015 年秋分为界，前期光照角周期性变化相对稳定，各特征点（分至点）之间的光照角出入相对较小；后期光照角呈现整体增大趋势，除夏至点外，其他特征点的光照角明显上升，但极值点分布规律仍保持。

降交点地方时同样具有年周期、双峰值的变化规律，主要由太阳在天赤道上的投影点运动速度变化所致。在春、秋分点附近运行慢，在夏、冬至点附近运行快。2014 年春分前后，降交点地方时达到最小值约AM 05∶50；其后，一直呈增大趋势，至2017年4 月，已经接近AM 08∶00。

轨道倾角具有年周期变化特点，主要由太阳引力摄动所致。当太阳在南半球时，摄动使倾角变大；当太阳在北半球时，摄动使倾角变小。另外，由于降交点地方时整体上由AM 06∶00 至AM 12∶00 方向运行，倾角还有整体逐渐减小的趋势。

日地距离因子变化也呈年周期规律，类似于正弦曲线，但是极值并非关于1.00 对称。极小值在冬至前后出现，极大值则在夏至前后出现，且前者偏离数值1.00 更明显。

从光照功率输入情况来看，距离越远，到达电池阵的功率越小；光照角越大，电池阵输入功率越小。因此，在夏至附近，电池阵的能源条件最差，因为距离远，光照角大。与之相反，冬至前后的能源条件则最好。但自2015 年秋分后，光照角整体上逐渐变大，能源输入呈恶化趋势，需要重点关注整星能源预算与平衡。

卫星搭载有GaInP2太阳电池，其安装面与太阳电池阵平面平行，GaInP2太阳电池法线与轨道法线也同向。电池规格为2 cm×2 cm，转换效率约为26.8%，表面覆盖Kapton 膜。4 片电池串联后经过40 Ω 电阻采样，得到的电压在2～3 V 之间。以下直接用电压表征电流，两者之间线性对应，仅存在40 Ω 的系数关联。

在卫星入轨早期阶段，GaInP2太阳电池的输出电流与遥测温度如图2 所示。入轨后期阶段，电流与遥测温度如图3 所示。为便于比较与分析，图3中仅选取冬至前后的遥测数据作为样本。

图2 早期GaInP2 电池电流与温度Fig.2 Current and temperature of GaInP2 cell at an early stage

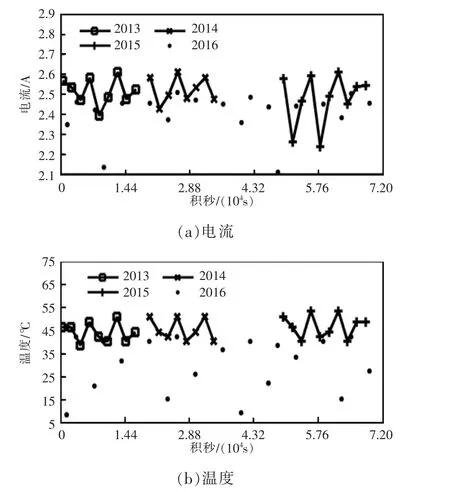
图3 后期冬至附近GaInP2 电池电流与温度Fig.3 Current and temperature of GaInP2 cell at a late stage near the winter solstice

图2 中，电流与温度参数变化具有轨道周期特性，电流极大值约为2.65 A，极小值约为2.50 A；温度极大值约为42.4 ℃，极小值约为33.4 ℃。温度变化与电流变化近乎同步，电流增大，温度升高；电流减小，温度降低。二者类似正弦规律变化。

在1 个轨道周期内，电流与温度的变化主要是地球反照所致。对于近地卫星的晨昏轨道情形，电流极值时刻所在的星下点基本上都在南、北极区域（夏至前后，北极区域反照最强，南极区域最弱；冬至前后，情形与夏至相反），这些区域由于冰雪覆盖，反照率相对较大，特别是南极附近还有较大的海面水域，也会产生较强的地球反照影响，电流极大值往往与之对应，同时，轨道周期中的电流极小值则在另一极区域出现。因此，反照越强，则电流越大，对应温度也越高。

短时间内光源功率起伏的影响以及卫星内部热控的影响，也可能会造成电流与温度的变化，这里暂不考虑。

在入轨后期，载荷调试工作完成后，对应的遥测数据采集模式改变，GaInP2太阳电池遥测采样率下降，如图3 所示。图3 中数据可以看作器件长期在轨运行的部分遥测结果。

因为采样率降低，电流数据短期的轨道周期性特征不再明显，但是长期性特征相对明显：早期电流相对较大，后期电流相对较小，一定程度上体现出GaInP2太阳电池功率的长期衰减性。

温度数据表现出振荡变化特点，2013 年温度相对较低；在随后2 年中，温度逐渐升高；2016 年温度又下降，且为最低水平。

一般而言，电池阵设计很少进行热控考虑，极少数国外卫星可能在电池阵背面有涂层设计，用于减小地球反照带来的热流影响。这里的温度变化可能是太阳光源功率变化所致，但是太阳光源功率难以在卫星上得到实测值。图4 为表征太阳活动强弱的参数之一F10.7 的观测值，F10.7 表示波长10.7 cm 的太阳射电流量，1 sfu=10-22W/（m2·Hz）。可以看出，卫星在轨期间，太阳活动大致处于中等强度水平；F10.7 曲线呈现两头低、中间高的特征，这与GaInP2电池温度的长期变化特征基本相符。

图4 F10.7 曲线（2010 年1 月1 日-2017 年5月22 日）Fig.4 F10.7 curve from 2010-01-01 to 2017-05-22

整体上，GaInP2太阳电池电流与温度在轨道周期内同步变化，而温度的长期变化又大致与太阳活动强弱同步。

2 功率衰减估计

单片的GaInP2电池功率P[12]可表示为

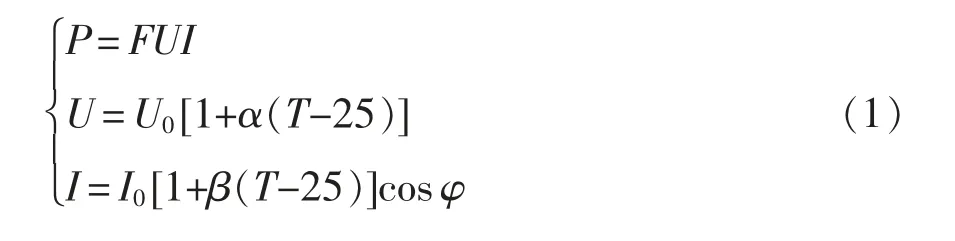
式中：U 为电池工作电压，V；U0为AM0 条件（太阳入射功率1 353 W/m2，温度25 ℃）下的开路电压，V；I 为电池工作电流，A；I0为AM0 条件下的短路电流，A；α 为电压温度系数，V/℃，一般为负值；β 为电流温度系数，A/℃，一般为正值；T 为电池的工作温度，℃；φ 为太阳的光照角，（°）；F 为功率系数，无量纲。功率系数主要受到以下因素：日地距离变化、空间环境以及遮挡、地球反照和光源功率波动等影响。

一般情况下，α 与β 的数值都很小，因此可以将式（1）简化为

式中，γ 为电池的功率温度系数，W/℃。本文对应的γ=-1.665×10-3W/℃。显然，U0与I0可以看作常数，故电池功率可以直接表示为

可见，式（3）与式（2）之间仅仅相差一个常数，故可以将GaInP2电池功率衰减估计转换为电流衰减估计。

传统衰减估计方法主要是在电池电流拟合的基础上针对日地距离因子、光照角和工作温度进行归一化，用归一化电流进行指数或者线性拟合，给出估计结果。这种归一化方法处理的不足是当输入的光源功率波动时，无法去除此影响，增加了估计误差。因为日地距离因子的归一化处理实际上是对功率传输链路的归一化，并没有涉及到光源功率的波动处理。

本文给出一种不同的针对光源功率波动的处理方法。首先进行电流正弦拟合，即

式中：D 为电流振幅，A；ω 为卫星的轨道周期，rad/s；t 为时间变量（遥测采集时刻），s；Ψ 为初相，rad；b为均值，A。这里采用正弦拟合的缘由可以参见图2中的电流变化规律。显然，均值b 就是式（3）中的I0。

得到电流的均值b 后，再进行太阳的光照角归一化处理，即

式中，b1为光照角归一化后的电流，A。

接下来，进行输出功率的温度归一化处理，即

式中，b2为针对输出功率进行温度归一化之后得到的电流，A。

针对输入功率波动，再次进行温度的归一化处理，即

式中：b3为针对输入功率进行温度归一化的电流，A；λT为温度归一化因子，无量纲。λT计算方法为

式中，Tr为参考温度，取273.15 K。

显然，这里将温度T 也转换为单位K 下的数值。输入功率温度归一化的理论基础为电池工作温度越高，说明入射到电池的光源功率越大，反之亦然。

至此，电池功率归一化工作完成。该方法主要是利用温度与光照角进行归一化，减少了日地距离归一化，相当于减少了一个误差源。

从以上处理中可以看出，温度数据的处理相对比较重要。由图2 可知，温度与电流几乎是同步变化，因此，也可以用正弦拟合方法求解一个轨道周期内的温度均值。图2 中的温度拟合结果如图5 所示。

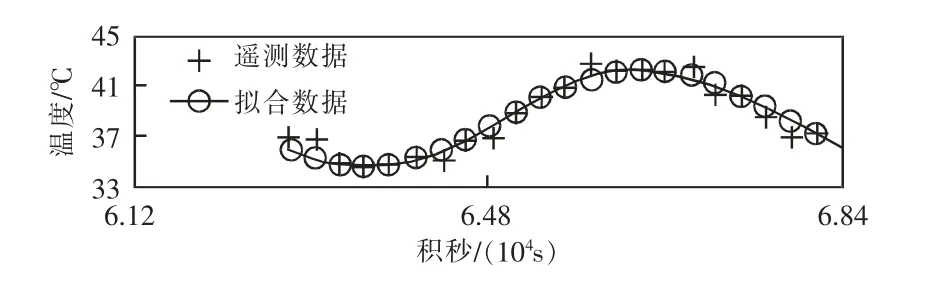
图5 电池温度拟合Fig.5 Fitting of battery temperature

在图5 中，为了便于比较，一并画出了遥测数据。拟合温度的均值约为38.4 ℃，振幅约为3.8 ℃；极值分别为42.2 ℃与34.6 ℃，振幅要略小于遥测数据情形，波动范围要小一些。以拟合曲线的极小值作为无地球反照时的输出，极大值作为地球反照下的最强输出，则地球反照作用最强时可抬升温度约22%，计算过程为3.8×2/（38.4-3.8）≈0.22。

对于电流拟合，与温度情形类似（见图2），这里不再进行画图与分析、讨论。

在新方法中，输入功率与输出功率都是针对温度进行归一化处理，有必要讨论温度影响下的估计误差。

以式（3）为例，如果不进行输出功率温度归一化，则对应的误差η 可以定义为

以功率温度系数γ=-1.665×10-3W/℃为例，得到的误差曲线如图6 所示。

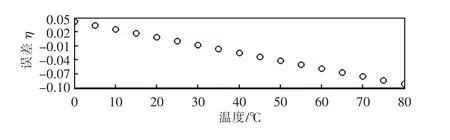
图6 不考虑输出功率温度归一化下的误差Fig.6 Error without the consideration of normalized output power or temperature

可以看出，当温度接近80 ℃时，η 接近-0.09，相对较大，因此，需要进行温度归一化处理。图5中，温度拟合的振幅约为3.8 ℃，则在温度归一化后引起的对应极值误差仅在-0.006 5 左右，再考虑一个轨道周期内多个采样点的平均效果，误差引起的均方差会更小。至于输入功率温度归一化后的误差影响，在结果中再分析、讨论。

最后，用线性拟合与指数拟合方法针对归一化电流进行衰减估计。线性拟合为

式中：im为归一化后的平均电流，A，即式（7）中的b3；k 为斜率，A/d；b0为截距，A；t 为时间变量，d。

指数拟合为

式中：c 为零值，A；ε 为衰减因子，d-1。

以上方法中对于电流处理相对简化，主要进行光照角归一化与温度归一化。这实际是在工程上将光照角和温度对应列为影响电流变化的第1 与第2 因素。电池温度主要受两方面因素影响：一是外部热流，例如光照、反照和其他器件辐射等；二是内部热流，主要是电流热阻效应引起的。因为温差原因，内、外热流之间存在传导耦合作用而相互影响，在这里，将外部热流考虑为主因。显然，在不考虑日地距离和太阳常数等变化的前提下，光照角变化也会引起电池温度变化，但在近500 km 高度的地球反照对于晨昏轨道的电池影响相对较大，而反照功率基本不随光照角变化，因此，温度处理在很大程度上是考虑了地球反照影响的归一化。

此外，从式（1）可以看出，温度对于电池电压和电流存在影响，作用于电池内部，在光电转换过程中，可将其归为电输出影响；而温度之于光功率变化，则可归为光电过程中的光输入影响。后者影响较大，可用电池温度归一化进行处理。

3 检验

利用2012 年冬至到2017 年春分的GaInP2电池电流与温度的遥测数据进行分析、检验。

因为晨昏轨道卫星在夏至前后会经历地影期，对应的电池电流会出现零值，温度也会出现较大跳动，在采样率较低的情况下，拟合误差较大，故这里未对夏至数据进行采样。

考虑到温度数据的重要性，先讨论温度数据的拟合、处理结果，如图7 所示。

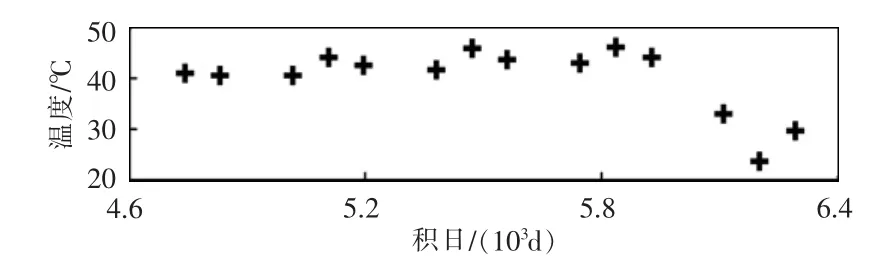
图7 电池温度拟合结果Fig.7 Fitting results of battery temperature

图7 中，温度结果为拟合得到的均值。可以看出，平均温度具有两端低、中间高的特征，这与前文图3 和图4 的分析结果相对符合。但是，末段的温度水平更低，这可能与轨道的光照有关。

定义轨道功率因子Fo为

式中，Fd为日地距离因子（参见图1），无量纲。显然，光照角越小、日地距离越近（日地距离因子越小），则轨道功率因子越大，表明到达电池的功率越强（假定光源功率无波动）。轨道功率因子如图8 所示。

图8 轨道功率因子Fig.8 Orbital power factor

由图8 可以看出，在卫星运行后期，轨道功率因子明显下降，说明这一时期轨道的光照条件相对较差，主要是光照角的逐渐增大所致。

综合图4 与图8 可知，在GaInP2电池工作后期，电池的功率下降既有光源功率波动因素（图4），又有轨道漂移因素（图8）。在这2 种因素作用下，电池输入功率低，对应的电池工作温度也低（图7）。这也说明，光源功率与电池温度存在对应关系，例如同步变化。

在温度归一化完成后，采用传统方法与新方法进行电流归一化。传统方法针对光照角、日地距离和输出功率进行归一化，新方法则针对光照角、输出功率和输入功率进行归一化，两者的功率归一化均以电池温度为参考。另外，新方法在输入功率归一化时分别以最高温度和最低温度为参考进行，即式（8）中的Tr分别为图7 中的最高温度与最低温度，可得到2 种不同结果，再加上原始电流的拟合结果，一共是4 种电流数据输出，如图9 所示。

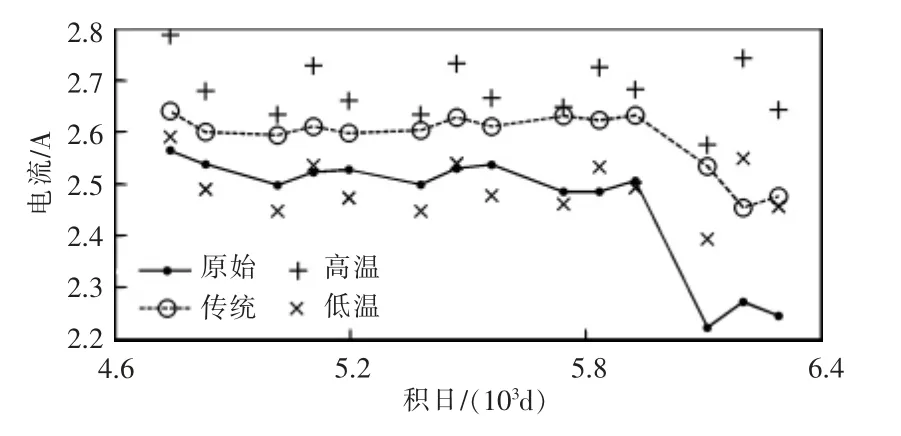
图9 电流归一化Fig.9 Normalized currents

图9 中，卫星入轨后的初期，电池功率衰减较快，这与绝大多数文献和地面测试结果基本相符。随后，电池进入功率缓慢衰减阶段，区别主要在于后期数据的不同。原始数据与传统方法下的数据在后期都出现明显下降，与图4 和图8 中后期数据情形类似，这说明光源功率下降（F10.7 数据末段）后，传统方法下的估计结果难以消除光源波动影响。

新方法下的2 条曲线在中后阶段都相对稳定，一致性较好（仅有2016 年秋分数据例外，经检查，2016 年秋分前后的温度遥测数据存在限幅现象，增大了对应的温度估计误差），特别是末段数据，明显减小了光源功率下降的影响。另外，2 条曲线的变化规律是同步的，仅仅是数值存在差异而已。因此，后续的衰减估计系数应该相同，只存在零值差别。

如果不考虑末段数据的差别，则新方法下年周期内数据间的差异要大于传统方法下的情形，后者的短期一致性实际上更好。其原因可能在于日地距离归一化，因此，后续还需考虑新方法下的日地距离归一化问题。但是，就全局长期的数据一致性而言，新方法应该更优。

此外，所有数据都表现出了季节差异性，大致上是冬至功率最强，春分次之，秋分最弱。最明显的差异在于2015 年与2016 年的冬至数据：新方法下的功率为极大值，保持了季节性变化规律；传统方法下的数据则是极小值，不同于前期数据变化规律。这也说明新方法下的全局数据一致性较好。

数据的季节性差异极有可能是地球反照所致。晨昏轨道下冬至与夏至时期的地球反照较为剧烈，电池输入功率波动明显；春分与秋分时期的影响则相对较小，功率波动较为缓和。这也表明，功率波动对估计结果有影响，需要尽力消除或者减小这一影响。

将图9 中的数据代入式（10）与式（11），得到的衰减估计结果如表1 所示，对应的年衰减率见表2。

表1 衰减估计Tab.1 Estimation of degradation

表2 年衰减率Tab.2 Annual degradation%

表2 中，年衰减率计算时1 a 取为365.242 5 d。显然，线性估计与指数估计的差别较大，前者的年衰减率是后者的3 倍左右；原始数据因为没有进行归一化处理，误差较大，对应的年衰减率最大；传统方法下指数估计的年衰减率在1%左右，这与硅太阳电池的衰减结果较为接近（文献[13]给出地球静止轨道卫星案例的年衰减率约为1%，文献[14]给出中地球轨道卫星的年衰减率约为1.7%，文献[15]给出低地球轨道、晨昏轨道卫星的年衰减率约为1.5%），未能体现出GaInP2电池的强抗辐照特性；新方法下指数估计的年衰减率为0.443%，明显低于文献[13-15]中的硅太阳电池阵估计结果，说明GaInP2电池的抗辐照特性要优于硅太阳电池。

文献[16]对国外20 世纪90 年代前后的砷化镓太阳电池衰减进行了地面测试与报道，给出的年衰减率在0.8%左右。考虑到地面测试中的辐照强度一般要大于空间真实情形，且地面设计中的功率预算也多偏于保守，因此，实际的年衰减率应该低于0.8%。比较而言，0.443%的功率衰减估计结果相对可信，而传统方法下的1%则显得相对保守。

同时，这里也以表1 和表2 中的指数估计结果作为最终结果输出。

不同情形下的拟合数据如图10 所示。图中，原始数据与传统方法下的拟合数据下降速率较快，对应的线性预测斜率绝对值也大；传统方法下的拟合数据正好处于高温、低温情形下的结果之间。

图10 不同情形下的拟合数据Fig.10 Fitting data in different scenarios

虽然高、低温情形下指数估计的年衰减率相同，但是零值并不相同，前者高、后者低。这对后续长寿命运行下的电池输出功率预测较为有利，可按功率的高低水平分别进行预测，给出输出功率包络。

以指数估计结果为参考，按照传统、高温、低温3 种情形进行功率预测，如图11 所示。图11 中预测是在当前数据截止点（2017 年春分）的基础上大致以季节为步进量向后延伸大约10 年进行。可以看出，高温与低温情形下的预测数据依然是同步变化，但传统方法下的预测结果明显衰减要快，大约在4 年后，其预测值即低于低温情形下的预测值。在轨15 年后，新方法下的功率衰减约为6.45%。

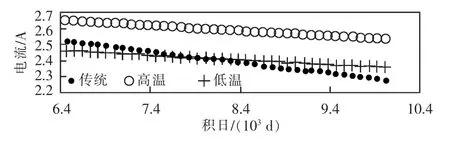
图11 指数预测Fig.11 Prediction of exponent

显然，预测值越大，卫星可能拥有的期望寿命越长。预测结果也显示，GaInP2太阳电池的抗辐照性能较好，适宜于近地空间场合下的长寿命能源或者电源应用。

在以上讨论中，新方法以电池工作温度为参考，对输入光照功率进行归一化，实际上对输入光照功率波动较大的长期应用场合较为有利，得到的结果也比传统方法下的结果更为可信。但是，新方法下的数据在短周期（年周期）内的波动反而更大，说明日地距离和地球反照等对输入光照功率的影响较大，后续需要进一步改进，例如按照季节分别进行衰减估计，则相同季节下的日地距离和地球反照相对稳定，误差可望更小。

4 结论

（1）对晨昏轨道近地卫星，太阳电池输出功率与工作温度在轨道周期内受地球反照影响明显，功率与温度曲线类似正弦变化，地球反照最强时可使温度抬升20%以上。

（2）新方法以太阳电池工作温度为参考，对输入光源功率进行归一化，然后再针对光照角和输出功率进行归一化，所得数据在长时段内的一致性较好，光源功率归一化效果相对明显，优于传统方法。

（3）GaInP2太阳电池具有较好的抗辐照性能，功率衰减因子约为-1.22×10-5/d，相应的年衰减率约为0.443%；预测在轨工作15 年后，功率衰减约为6.45%。

（4）国产空间太阳电池功率长期衰减小，适宜于近地空间的长寿命应用。

后续工作中，还需积累更多的GaInP2太阳电池功率相关数据，结合高、中、低不同轨道类型进一步检验和改进新方法。重点以季节为分层，分别进行功率衰减估计，为在轨卫星长期管理的遥测诊断、能源估计与预测以及器件健康状态评估等提供数据和技术支持。