基于代理模型的结构优化设计

丁镜之

（沈阳航空航天大学航空宇航学院 辽宁沈阳 110136）

使用代理模型对飞机结构进行优化，从而减少了使用常规方法的计算量，缩短了飞机结构设计的周期，更为飞机的其他设计奠定了良好的基础。比如对一个高精度模型进行仿真时，计算时间可能需要几小时甚至几天才能完成。针对如此耗时的不易求解的计算，可以使用具有少量计算和快速求解的代理模型来完成。[1]针对常规基于可靠度的结构优化中，涉及嵌套循环（内循环求解结构可靠度，外循环求解最优设计），即便使用代理模型，对于复杂大型结构基于可靠度的结构优化成本有时也是难以接受的。为提高结构可靠度优化效率，本文针对基于可靠度结构优化的特点，提出了逻辑回归Kriging代理模型。[2]

一、逻辑回归Kriging模型

逻辑回归Logistic regression（LR）是一种回归分析方法，用来探讨一个分类结果变量与几个解释变量之间的关系。LR与线性回归模型的区别在于取两个或两个以上的可能值时，LR结果变量是离散的。[3]

LR的原始形式如下：

二、逻辑回归Kriging模型构建步骤

三、算例

式中：w和t分别是杆横截面的宽度和厚度；L是长度D0是允许位移，X为屈服强度；Y和Z是负载；E是弹性模量。确定性参数包括d=[w，t，L，D]，w和t是设计变量，L=100，D0=2.5，随机变量Xr=[X，Y，Z，E]是独立的，其中X均值为40000，标准差为2000；Y均值为1000，标准差为100；Z均值为500，标准差为100；E均值为29×106，标准差为1.45×106。设计目标为杆的横截面积最小化，目标的失效概率为，RBDO的表达式定义为：

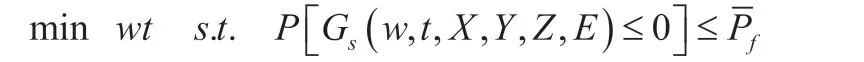
对于本例，初始设计点为w=2和t=4。不同方法的计算结果见表1。在效率方面，LR-LK/FORM方法只需要调用目标函数26次，但是它比LR-LK/AK-MCS方法需要更多的LSF调用；在精度方面，LR-LK/AK-MCS方法能够很好地满足概率约束，具有很高的精度。

表1 优化结果

四、结束语

本文主要介绍了逻辑回归与Kriging模型相结合的理论原理，逻辑回归的基本概念、逻辑回归与Kriging模型相结合的基本思路。用流程图阐明了构建RKM构建流程。通过算例表明：文中构建的逻辑回归Kriging模型具有满意的计算精度，对比极限状态函数调用次数，文中方法具有更高的计算效率。