基于机载激光雷达点云和随机森林算法的森林蓄积量估测*

孙忠秋 高金萍 吴发云 高显连 胡 杨 高剑新

(1.国家林业和草原局调查规划设计院 北京 100714； 2.宁夏大学生态环境学院 西北土地退化与生态恢复国家重点实验室培育基地西北退化生态系统恢复与重建教育部重点实验室 银川 750021)

森林是陆地生态系统的主体，具有调节气候、涵养水源、防风固沙、减少污染、改善生态环境等重要作用，在山水林田湖草生命共同体中处于不可或缺的基础地位。森林蓄积量指一定森林面积上全部树木材积的总和(孟宪宇， 1996； Nilsson， 1996)，是反映一个国家或地区森林资源总规模和水平的基本指标之一，与木材安全、气候变化、动物栖息等密切相关，可为制定森林经营管理方案提供科学依据(李崇贵等， 2006； 徐济德， 2014)，准确估测森林蓄积量对提高森林资源管理水平和生态环境保护建设具有重要意义(Næsset， 2002； 陈新云等, 2019； 闫飞， 2014)。传统大面积森林蓄积量估测主要根据国家森林资源规划设计调查技术规程，通过对标准样地相关因子的实测或用角规测量的方法，基于不同树种材积公式计算样地或小班蓄积量(李崇贵等， 2006)，进而推算区域森林蓄积量； 此项工作精度高，但耗时耗力，在地形复杂的林区往往无法开展。近年来，随着遥感应用技术不断发展，利用遥感影像结合地面样地信息估测森林蓄积量成为可能。目前，大部分研究基于不同卫星遥感影像数据源，如Landsat、Sentinel-2、高分系列、MODIS等(Chenetal.， 2012； Gireeetal.， 2013； 王月婷等， 2015； 杨柳等， 2017； 王佳等， 2014)，结合少量地面样地调查数据，应用数学算法建立森林蓄积量估测模型； 然而，由于光学遥感影像只能获取森林的水平结构信息，不具备获取森林垂直结构信息的能力，因此导致森林蓄积量估测精度普遍偏低。如李世波等(2019)基于GF-1影像估测森林蓄积量，模型估测精度(R2)仅0.50左右。

激光雷达是一种新兴的主动遥感技术，其突破了传统光学遥感的光谱局限性，能够穿透森林冠层，获取森林三维结构信息，在森林资源监测中正逐渐发挥作用(Nilsson， 1996； Næsset， 1997； 曹林等， 2013； 李增元等， 2016)。学者们利用机载激光雷达数据反演林分平均高、生物量、郁闭度等森林参数，均取得了比传统光学遥感精度更高的结果(Næssetetal.， 2001； 2002； 2005； 段祝庚等， 2016； 耿林等， 2018)。汤旭光(2013)基于ICESat-GLAS大光斑激光雷达数据先估测林分平均高，再进行森林生物量建模，得出针叶林样地的估测精度(R2)为0.82。刘美爽等(2014)采用ICESat-GLAS数据对吉林省汪清林业局林区的林分冠层高度进行估测，得出该区域的估测精度(R2)为0.84。吴迪等(2014)基于ICESat-GLAS数据，结合黑龙江省塔河林场109块标准地调查数据，采用随机森林算法对该地区林分平均高进行估测，R2为0.72，RMSE为1.83 m。Hollaus等(2007)利用小光斑激光雷达数据估测奥地利福拉尔贝格州高山地区森林蓄积量，R2= 0.89，RMSE = 90.90 m3·hm-2。刘琪璟等(2008)基于日本长崎县小光斑激光雷达数据估测林分平均高，其误差为0.4～0.5 m。高婷等(2017)使用小光斑激光雷达数据估测甘肃张掖大野口林区林分平均高，R2=0.81。Sheridan等(2014)基于一元和多元线性回归模型探索小光斑激光雷达数据估测美国俄勒冈州东部迈哈尔国家森林公园森林蓄积量的能力，得出一元和多元线性回归的蓄积量估测模型R2分别为0.83和0.88。

由于ICESat-GLAS大光斑激光雷达数据可以免费获取，目前基于大光斑激光雷达数据进行森林参数提取的研究较多，使用小光斑激光雷达数据进行森林参数提取的研究较少。本研究以全覆盖的有人机机载激光雷达点云数据和每木检尺的地面样地数据为数据源，提取样地点云高度参数和郁闭度等特征，采用随机森林算法构建森林蓄积量估测模型，同时对激光雷达生成的森林参数进行变量筛选，确定蓄积量估测中重要的森林参数，最终确立以样地为基本单元的森林蓄积量估测模型，分析机载激光雷达数据在森林蓄积量反演方面的潜力，以期为森林蓄积量高效准确估测提供方法依据。

1 研究区概况

以大兴沟林业局为研究区，该区位于吉林省东部、延边朝鲜族自治州东北部，属图们江流域嘎呀河支流的中游(129°05′—130°01′E，43°20′—43°40′N)，总面积128 097 hm2。地势东西两端山高坡陡，山脉起伏较大，中部逐渐降低，东西沟中下游地段稍为平缓，平均坡度15°左右。属温带大陆性季风气候，年平均气温2 ℃左右，无霜期105～125天。境内植被属长白山植物区系，大多为阔叶林和针阔混交林。人工林以落叶松(Larixspp.)林居多，其次为红松(Pinuskoraiensis)林。常见的天然乔木树种有红松、云杉(Piceaasperata)、冷杉(Abiesfabri)等针叶树种，黄檗(Phellodendronamurense)、水曲柳(Fraxinusmandshurica)、胡桃楸(Juglansmandshurica)、椴树(Tiliatuan)、蒙古栎(Quercusmongolica)、白桦(Betulaplatyphylla)等阔叶树种。研究区内森林资源丰富，是东北林区林业研究的重点区域之一(图1)。

图1 研究区森林及样地分布Fig. 1 Forest and sample plot distribution of research area

2 数据及预处理

2.1 样地调查数据

采用2018年10月“陆地碳卫星吉林重点林区综合试验地面样地调查”项目获取的数据，其中大兴沟林业局区域共调查232块半径15 m的圆形样地。

2.1.1 样地位置 样地位置对后续建模精度影响较大，为保证调查样地类型具有代表性，样地选择主要基于以下原则： 1) 依据2016—2018年东北内蒙古重点国有林区森林资源规划设计调查数据，对小班中布设角规样地树高数据进行分析，得到蓄积量排名前10的森林类型(云杉、冷杉、落叶松、桦木、杨树、椴树、栎类、针叶混、针阔混和阔叶混)，并按照5个树高级梯度(最大值与最小值之间划分出5个区间)和3个郁闭度级梯度(低0.20～0.39、中0.40～0.69、高0.70以上)进行划分； 2) 选择的样地不在同一坡面或坡向； 3) 2块样地之间距离超过500 m； 4) 同类型单元样地布设在不同起源的森林、不同地形的森林。

2.1.2 样地调查 为保证后续样地与激光雷达点云在空间上精确配准，采用三基站联合差分定位技术对样地中心和样木定位，并记录坐标。调查内容包括胸径、树高、枝下高、冠幅、郁闭度、起源、树种组成等信息。利用R软件从232块样地中随机抽取70%数据作为训练样本(164块样地)，剩余30%数据作为验证样本(68块样地)，样地统计信息和分组情况见表1。

表1 样地蓄积量统计信息Tab.1 Sample stand stock volume statistics

2.2 有人机机载激光雷达数据

有人机机载激光雷达数据于2018年8月由搭载在塞斯纳208B有人机平台上的RIEGL-VQ-1560i激光雷达航摄仪获取。该设备是超高性能、高度集成的双通道机载激光扫描仪系统，能够在不同高度飞行作业获取大范围高密度点云，适合对大面积区域和复杂环境进行空中测绘。本研究中，飞机设计航飞相对航高1 800 m，飞行速度(相对地面)240 km·h-1，激光器发射频率2 000 kHz(两通道同时工作，单通道频率1 000 kHz)，此参数下获取的激光点云密度为每平方米10个点； 但由于地形起伏因素影响，最终成果约每平方米13个点。有人机机载激光雷达数据概况见表2。

表2 有人机机载激光雷达数据概况Tab.2 An overview of airborne LiDAR data

数据获取时采用的测绘基准如下： 1) 坐标系统， 2000国家大地坐标系； 2) 高程基准， 1985国家高程基准； 3) 投影方式， 高斯克吕格投影，3°分带，东偏500 km，加带号，中央子午线129°。激光雷达数据对研究区全覆盖，总面积约1.2×105hm2。数据存储采用LAS 1.2格式的点云，数据量约1.72 TB。

2.3 数据准备和建模流程

在数据准备阶段，首先对研究区点云数据进行预处理，去除异常点并分类，分离地面点； 然后进行样地和点云的几何配准，该过程需选取大量同名点位，因研究区森林覆盖率高，同名点选取困难，耗时较长。完成样地点云数据裁切后，即进入数据建模阶段，分别提取训练样地和验证样地点云的高度参数和郁闭度，采用随机森林算法建模并进行精度评价。数据准备和建模流程如图2所示。

图2 蓄积量估测流程Fig. 2 Flow chart of forest stock volume estimation

2.4 数据预处理

2.4.1 样地蓄积计算 首先按照表3进行树种组归并，然后基于一元材积公式计算样地总蓄积。蓄积量计算通用公式(E·N·楚里克等， 1989)如下：

表3 树种组基本信息Tab.3 Tree species group basic information

式中：V为样地总蓄积；N为样木株数；D为样木胸径；a、b、c、d、e、k为材积公式中的系数，根据《中国立木材积表》吉林省立木材积表(刘琪璟， 2017)确定。

2.4.2 激光雷达点云数据预处理 激光雷达原始点云数据经姿态校正、噪声点剔除、坐标转换、航带拼接、系统差改正等预处理形成1∶10 000比例尺分幅成果数据。本研究在分幅成果数据上利用LiDAR360软件进行点云数据拼接、点云滤波、点云分类等，最终获得用于建模的激光雷达点云数据。

2.4.3 样地点云数据提取高度参数 基于样地点云数据，采用数学统计方法可以提取多个与高度相关的参数，即根据指定的高度间隔将其进一步分割成不同的“层”，统计各层的点数。建模中常用的高度参数有最大高(Hmax)、最小高(Hmin)、平均高(Hmean)、高度中位数(Hmedian)、高度百分位数(H%)和高度标准差(Hstd)等。其中H%的计算方法如下： 某一统计单元内，将其内部所有归一化的激光雷达点云按高度排序，计算每一统计单元内X%的点所在高度即为该统计单元的高度百分位数(图3)。建模中使用的高度百分位数包含15个，即1%、5%、10%、20%、25%、30%、40%、50%、60%、70%、75%、80%、90%、95%和99%。

图3 激光雷达点云高度百分位数Fig. 3 Height percentile of LiDAR point cloud

2.4.4 样地点云数据提取郁闭度 样地点云的郁闭度定义为植被回波点数与总点数的比值。本研究将植被高度阈值设为2 m，在计算过程中大于高度阈值的点均被认为是植被点，公式如下：

式中：Pc为郁闭度；Nveg为植被回波点数；Ntotal为总点数。

输出值范围为0(没有林冠层覆盖/完全裸露)～1(全植被覆盖)。提取的郁闭度与样地实测郁闭度作差，差值均值为0.08，标准差为0.14，二者具有很好的一致性。

3 建模方法

蓄积量模型的构建一般使用两大类方法(Shaoetal.， 2017； Takmaetal.， 2012)。一是参数化方法，构建由有限数量的参数定义或参数化的模型，该方法需要作出某些先验假设，且采用测试数据以确保不违反这些假设，有时还需要对变量进行适当转换。参数化方法能够很好解释待测参数与变量之间的相关关系，但缺点是获取新数据必须重新构建新模型。在众多蓄积量估测研究中，多元线性回归是最常用的方法，通过对实测蓄积量与激光雷达提取变量之间的关系进行回归分析，得到蓄积量估测模型，利用验证样地数据和一系列检验指标可以验证模型精度。二是非参数化方法，与参数化方法相比，该方法无需先验假设，模型构建更便捷。机器学习算法是典型的非参数化模型构建方法，尽管该类算法不能得出具体模型，但并不影响算法的回归预测，且机器学习算法的预测结果往往高于传统的线性回归方法(García-Gutiérrezetal.， 2015； Yuetal.， 2008； 2011)。因此，本研究采用机器学习算法中的随机森林算法构建森林蓄积量估测模型。

3.1 随机森林算法

随机森林算法是由Breiman(2001)提出的，其具体建模步骤如下： 对输入随机森林模型的训练样本进行随机采样，包括行(单个样本)和列(特征变量)2个维度。行采样使用Bootstrap算法，列采样为从M个特征变量中随机选择mtry(mtry≤M)个特征变量。基于上述步骤，构建k株决策树，通过求取平均值得到最终预测结果。随机森林回归公式可表示为Y=Eθh(X,θ)。利用袋外数据(out of bag, OOB)计算每株决策树的预测误差，每株决策树的平均泛化误差(generalization error,GE)计算公式为：

GE=EθEX,Y[Y-h(X,θ)]2。

式中：θ为随机变量；Eθ为期望函数；X、Y为训练集抽取的随机变量；h为决策树预测函数；EX,Y为X、Y的联合期望函数。

使用R软件Random Forest 包，经多次试验确定决策树数目(ntree)和节点分裂时变量个数(mtry)，代入随机森林回归模型，并利用回归模型对验证样本进行预估。

3.2 变量筛选

建模过程中变量个数越多，运算量越大，耗时越长，通常需要进行有效的变量筛选，以在不损失建模精度的前提下降低运算量。本研究运用R软件VSURF(variable selection using random forests)包进行变量筛选，主要包含3个步骤。1) 阈值处理： 首先，在ntree和mtry默认设置下，采用随机森林算法的重要值函数计算参数nfor.thres rf； 然后，按变量的平均变量重要性(variable importance, VI)降序排序； 接下来，计算阈值min.thres，修剪的CART树的最小预测值拟合到VI的标准偏差曲线； 最后，计算阈值，仅保留平均VI大于nmin*min.thres的变量。2) 解释： 考虑步骤1选择的变量，采用nfor.interp函数，首先，只选择最重要的变量，直到计算完第一步选择的所有变量结束； 然后，采用err.min函数计算模型的最小平均袋外(OOB)误差及其相关的标准偏差sd.min； 最后，选择平均OOB误差小于err.min+nsd*sd.min的最小模型(及其相应的变量)。3) 预测： 起点与步骤2相同，但是现在变量逐步添加到模型中，使用步骤2遗漏的变量和mean.jump计算平均跳跃值，并设置为一个模型的平均OOB误差与其第一个跟随模型之间的平均绝对差值，如果平均OOB误差减小大于nmj*mean.jump，则变量包含在模型中。通过VSURF包设置的3个步骤，对蓄积量估测相对不重要的变量会被移除，筛选后的变量用于构建森林蓄积量估测模型。

3.3 模型评价

采用决定系数(coefficient of determination,R2)、均方根误差(root mean square error, RMSE)评价模型拟合优度(Huetal.， 2019)，采用相对均方根误差(relative RMSE, rRMSE)、平均绝对误差(mean absolute error, MAE)和平均相对误差(mean relative error, MRE)评价模型估测精度。决定系数(R2)为自变量变异程度占总变异程度的比例，R2越大，表示模型拟合能力越强。均方根误差(RMSE)为标准误差的算术平方根，用于衡量预测值与真实值之间的偏差，RMSE越小，表示模型预测能力越强。相对均方根误差(rRMSE)为RMSE与估测结果算术平均值的比值，与评价量本身数量级水平无关，能够更好体现总体值域差别较大的模型预测精度(张瑞英等， 2016)，rRMSE越小，表示模型预测效果越好。平均绝对误差(MAE)为绝对误差的平均值，可以反映预测值误差的实际情况。平均相对误差(MRE)可以反映模型的预估精度。5个指标的计算公式如下：

4 结果与分析

4.1 输入参数与最优模型参数选择

本研究对比2种情况下的建模效果，具体输入变量如表4所示。

表4 输入变量Tab.4 Input variables

随机森林模型好坏由mtry和ntree决定。对于回归问题，mtry 默认设置为全部自变量数量的1/3(取整)，ntree一般取500(本研究也取值500)。通常，mtry 取默认值不一定能获取最优模型，选择合适的mtry可以降低随机森林模型的预测误差(欧强新等， 2019)，因此本研究对mtry进行调优。利用高度参数建模，参与计算的变量为23个，1≤mtry≤23。图4为23个模型的评价指标。

由图4可知，当mtry=17时，模型具有最小的RMSE(18.01 m3·hm-2)、最小的rRMSE(14.02%)、最小的MAE(13.07 m3·hm-2)和相对较小的MRE(16.28%)； 当mtry=1时，模型具有最大的RMSE(20.17 m3·hm-2)、最大的rRMSE(15.97%)、最大的MAE(15.14 m3·hm-2)和最大的MRE(17.93%)。整体趋势是： 当mtry≤17时，RMSE、rRMSE和MAE不断减小； 当mtry>17时，RMSE、rRMSE、MAE和MRE显著升高。所有模型的R2均在0.96附近，变化不明显。故选取mtry=17作为最优模型参数，此时，ntree最优参数值为64(图5)。

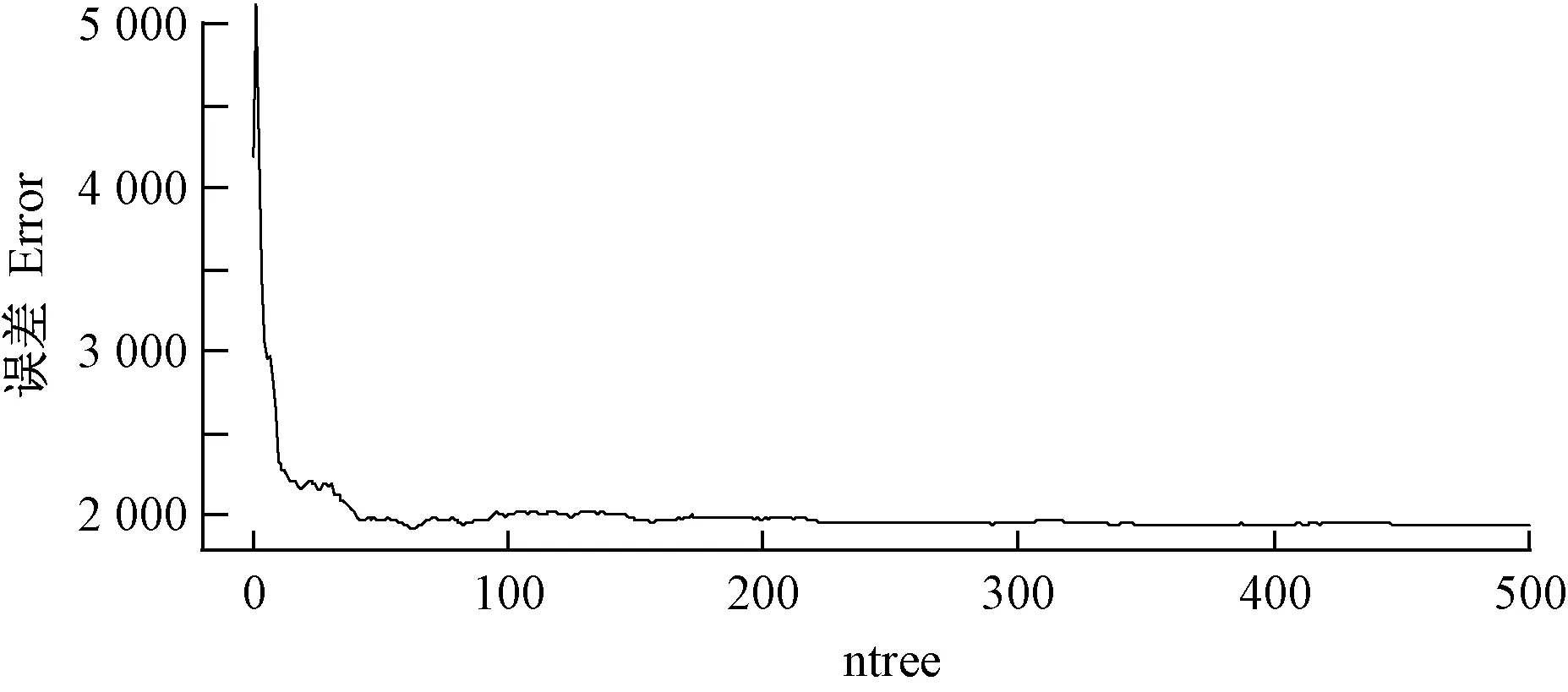
图5 高度参数建模ntree最优参数值确定Fig. 5 Optimal ntree parameter of height parameter modeling

联合高度参数和郁闭度建模，参与计算的变量为24个，1≤mtry≤24。图6为24个模型的评价指标。

据《财经》报道，阿里内部对于杨伟东的调查已经持续一段时间，杨伟东此次涉嫌贪腐的项目主要集中在优酷于2018年推出的“这就是”系列综艺，主要是关于综艺项目的收支问题。该系列综艺以《这！就是街舞》打头阵，后陆续推出了《这！就是灌篮》等。

由图6可知，当mtry=22时，模型具有最小的RMSE(16.94 m3·hm-2)、相对较小的rRMSE(13.18%)、最小的MAE(12.44 m3·hm-2)和最小的MRE(15.32%)； 当mtry=1时，模型具有最大的RMSE(19.46 m3·hm-2)、最大的rRMSE(15.45%)、最大的MAE(14.47 m3·hm-2)和最大的MRE(17.59%)。整体趋势是：R2变化不明显，当mtry≤22时，RMSE、rRMSE、MAE和MRE不断减小； 当mtry>22时，RMSE、rRMSE、MAE和MRE显著升高。故选取mtry=22作为最优模型参数，此时，ntree最优参数值为406(图7)。

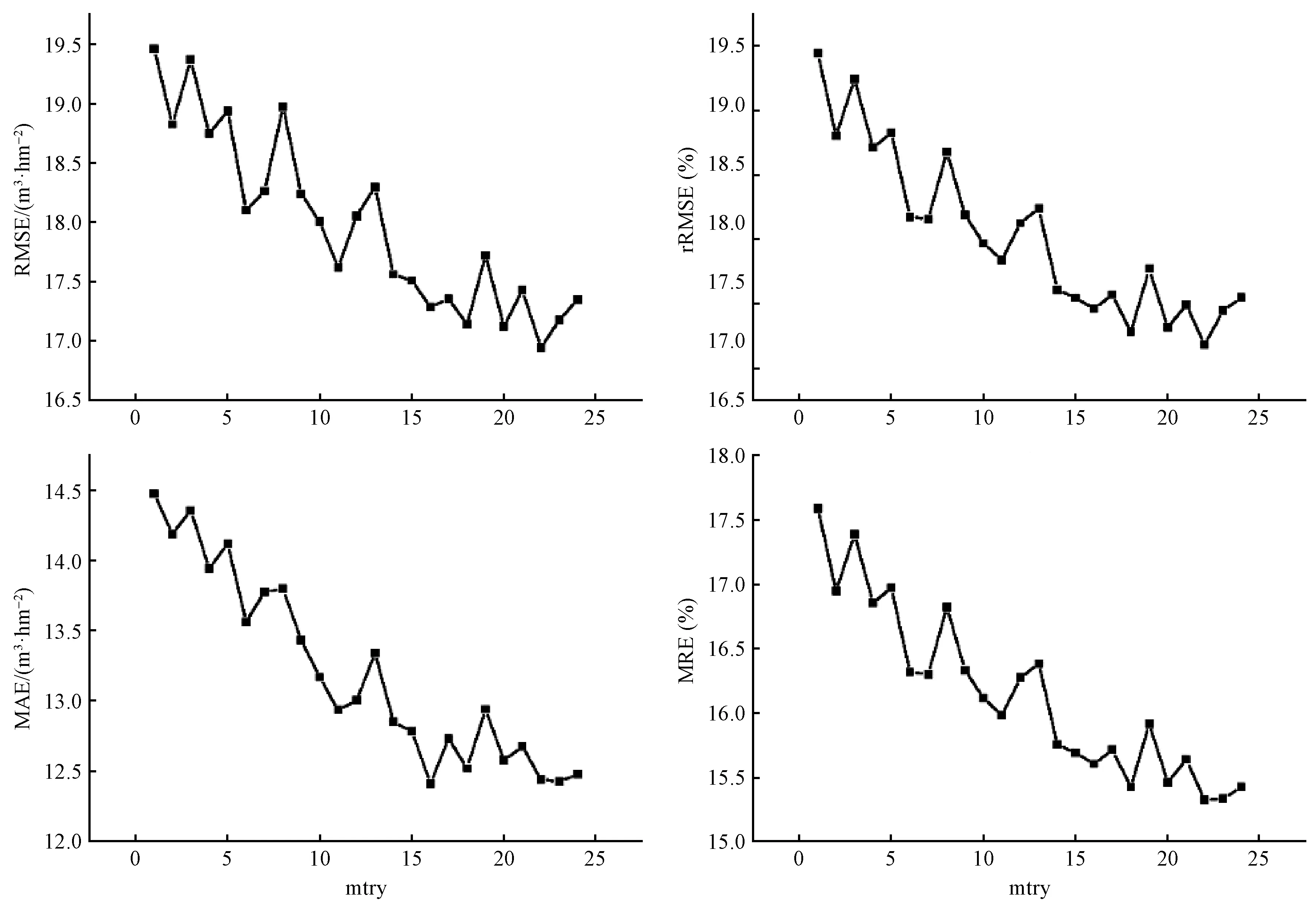
图6 联合高度参数和郁闭度建模评价指标Fig. 6 Evaluation indicators of height parameter and crown density modeling

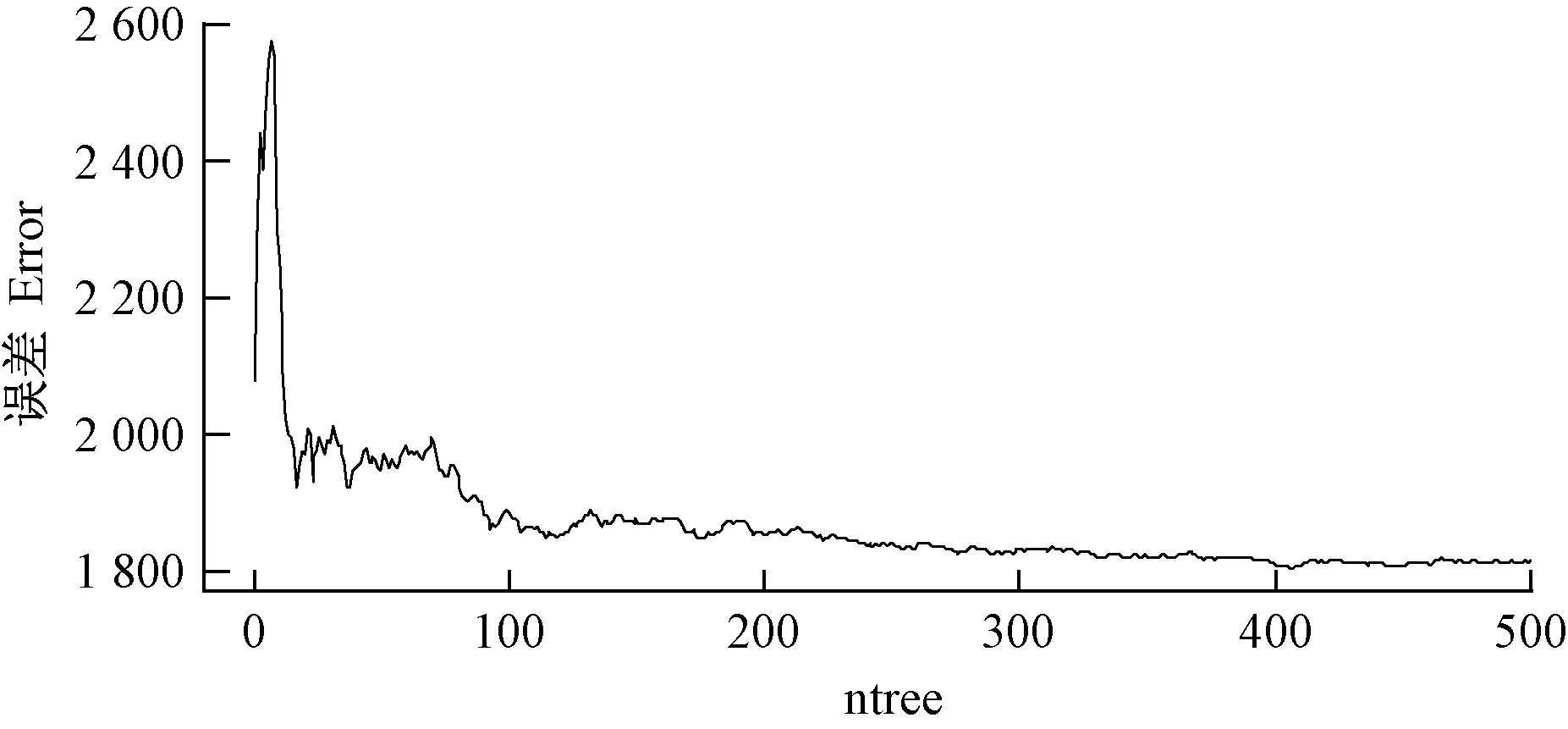
图7 联合高度参数和郁闭度建模ntree最优参数值确定Fig. 7 Optimal ntree parameter of height parameter and crown density modeling

4.2 建模结果

图8、9分别给出了上述最优随机森林模型在训练样本和验证样本中的精度。由图8可知，仅用高度参数建模，训练阶段的估测精度为R2=0.96、RMSE=18.01 m3·hm-2、MAE=13.07 m3·hm-2、rRMSE=14.02%、MRE=16.28%； 验证阶段的估测精度为R2=0.75、RMSE=40.07 m3·hm-2、MAE=29.21 m3·hm-2、rRMSE=36.20%、MRE=49.40%。由图9可知，联合高度参数和郁闭度建模，训练阶段的估测精度为R2=0.97、RMSE=16.94 m3·hm-2、MAE=12.44 m3·hm-2、rRMSE=13.18%、MRE=15.32%； 验证阶段的估测精度为R2=0.79、RMSE=36.23 m3·hm-2、MAE=26.16 m3·hm-2、rRMSE=32.73%、MRE=38.35%。

图8 仅用高度参数(23个变量)估测森林蓄积量(左： 训练模型结果； 右： 验证模型结果)Fig. 8 Estimation forest stock volume only using height parameters(left： training result; right： validation result)

图9 联合高度参数和郁闭度(24个变量)估测森林蓄积量(左： 训练模型结果； 右： 验证模型结果)Fig. 9 Estimation forest stock volume using height parameters and canopy density(left： training result; right： validation result)

对比分析2种情况下的建模结果可知，增加郁闭度信息后，模型R2升高，RMSE、rRMSE、MAE和MRE均显著下降。可见在森林蓄积量建模时，增加林分郁闭度信息能够提升模型精度。

4.3 变量筛选与建模结果

运用R软件VSURF包对上述高度参数和郁闭度变量数据集进行变量筛选，过程如图10所示。通过计算各变量重要性均值、变量重要性标准差和模型OOB误差，在所有提取24个变量中，最终筛选出7个变量用于建模，分别为最大高(Hmax)、平均高(Hmean)、郁闭度(Pc)、50%高度百分位数(H%8)、60%高度百分位数(H%9)、高度的二次幂平均(Hsqrt_mean_sq)和高度方差(Hvar)。筛选后变量的重要性排序如图11所示。

图10 基于VSURF包筛选变量Fig. 10 Variable selection based on VSURF package

图11 筛选后变量的重要性排序Fig. 11 The importance of selecting variables

在最优筛选变量情况下，图12给出了随机森林模型在训练样本和验证样本中的估测精度。训练阶段的估测精度为R2=0.97、RMSE=17.24 m3·hm-2、MAE=12.76 m3·hm-2、rRMSE=13.42%、MRE=14.76%； 验证阶段的估测精度为R2=0.79、RMSE=36.50 m3·hm-2、MAE=26.08 m3·hm-2、rRMSE=32.97%、MRE=38.05%。

对比变量筛选前后的建模结果(图9、图12)可知，在模型训练阶段，经变量筛选后的模型R2未降低，但是RMSE、rRMSE、MAE上升； 在模型验证阶段，经变量筛选后的模型R2未变化，RMSE从36.23 m3·hm-2升至36.50 m3·hm-2，rRMSE从31.92%升至32.97%，MAE从26.16 m3·hm-2降至26.08 m3·hm-2，MRE从38.35%降至38.05%。可见，经变量筛选后，模型精度虽有变化，但是差别不大，因此可直接用筛选后的变量进行建模。

为了进一步验证随机森林算法在训练和验证阶段所得结果的稳定性，本研究额外增加10次独立重复试验与图12结果进行对比，10次独立重复试验的模型训练阶段结果如表5所示、验证阶段结果如表6所示。由表5可知，R2的平均值为0.96，RMSE的平均值为17.36 m3·hm-2，MAE的平均值为12.56 m3·hm-2，rRMSE的平均值为13.84%，MRE的平均值为14.00%，与图12训练模型结果基本一致； 由表6可知，R2的平均值为0.78，RMSE的平均值为40.30 m3·hm-2，MAE的平均值为28.74 m3·hm-2，rRMSE的平均值为33.57%，MRE的平均值为34.39%，与图12验证模型结果也基本一致。这说明，数据随机分组后在随机森林算法下的建模预测结果具有很好的一致性。

图12 基于筛选变量估测森林蓄积量(左： 训练模型结果； 右： 验证模型结果)Fig. 12 Estimation forest stock volume using selection variables(left： training result; right： validation result)

表5 10次建模训练结果Tab.5 Ten times results in the training phases

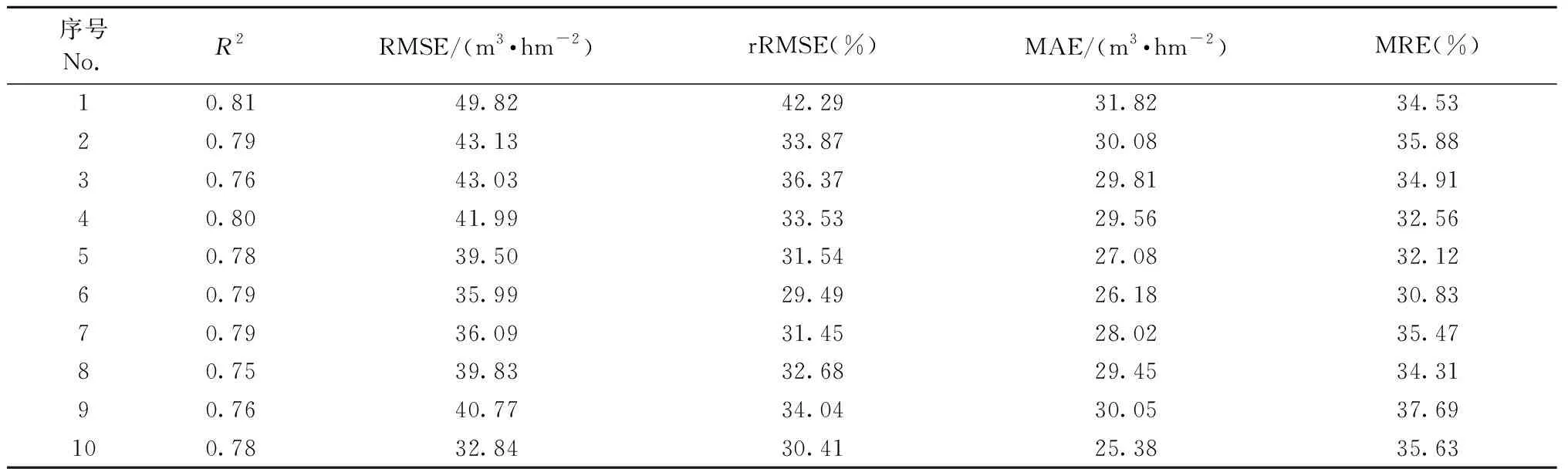
表6 10次建模验证结果Tab.6 Ten times results in the validation phases

5 讨论

采用随机森林算法对基于机载激光雷达点云数据提取的不同变量进行建模，模型精度均很高，随机森林算法的适应性较强。仅用高度参数建模的估测精度为R2=0.75、RMSE=40.07 m3·hm-2、MAE=29.21 m3·hm-2、MRE=49.40%，联合高度参数和郁闭度建模的估测精度为R2=0.79、RMSE=36.23 m3·hm-2、MAE=26.16 m3·hm-2、MRE=38.35%，说明基于机载激光雷达点云估测森林蓄积量时，增加林分郁闭度信息是提高建模精度的重要途径。Hu等(2020)基于哨兵2号光谱数据联合机器学习算法和多元线性回归方法估测森林蓄积量，得到的最优建模精度仅为R2=0.58、RMSE=65.03 m3·hm-2。Chrysafis等(2017)探讨Sentinel-2和Landsat-8估测森林蓄积量的能力，结果分别为R2=0.63、RMSE=63.11 m3·hm-2和R2=0.62、RMSE=64.40 m3·hm-2。相较其他研究，本研究在基于激光雷达点云数据提取的变量下，不同形式的变量组合均取得了较好结果。与传统光学遥感影像相比，取得较好结果可能基于以下3点原因： 一是激光雷达穿透能力较强，能穿透林分到达地面，直接获取林分高度等垂直结构信息，与光学遥感影像只能获取林分水平结构信息不同，垂直结构信息估测森林蓄积量更有效(Limetal.， 2009)； 二是本研究采用参数优化的随机森林模型，以RMSE为标准分别计算模型的最优变量，使得模型具有更好的估测能力(欧强新等， 2019)； 三是本研究区位于我国东北地区，地形和森林结构相较于南方等研究区可能比较简单(李崇贵等, 2006)。目前也有一些基于激光雷达点云数据的森林参数研究，如庞勇等(2011)采用小光斑激光雷达数据、ICESat-GLAS大光斑激光雷达数据和光学遥感影像数据，以78块地面样地作为真值，对大湄公河次区域森林生物量进行估测，建模估测相关系数为0.70，相比本研究结果略差，可能是南方地区复杂的地形环境和较少的样本量造成的。曹林等(2014)以江苏常熟虞山林场为研究区，采用逐步回归方法得到森林蓄积量最优估测结果的决定系数仅为0.55，其精度较低的原因主要有3点： 1) 模型选择得不好，与随机森林算法相比，逐步回归方法的表现能力较差，这是造成其估测精度较低的最主要原因； 2) 样本量较少，其研究仅有73块地面样地数据，数据在建模时代表性可能不足； 3) 相较于北方地区，江苏常熟虞山林场地形可能更复杂。刘浩等(2018)基于江苏东台林场55块地面样地数据，得出小光斑激光雷达数据估测该地区人工林森林蓄积量精度的调整R2=0.84、rRMSE=14.27%，结果要略好于本研究，主要原因是其研究对象为人工林，林型相对较简单，估测信息提取较好。Holmgren(2004)对比研究不同点云密度估测瑞典西南部地区森林蓄积量的能力，得到蓄积量的最优估测均方根误差为31.00 m3·hm-2，略优于本研究(36.23 m3·hm-2)，说明点云密度是影响蓄积量估测结果的一个重要因素。

此外，本研究充分评估了郁闭度对森林蓄积量估测的影响，结果发现，增加林分郁闭度信息可提高模型估测森林蓄积量的能力，R2由0.75提高到0.79，RMSE从40.07 m3·hm-2降至36.23 m3·hm-2，说明采用机载激光雷达点云数据反演森林蓄积量时，辅助林分郁闭度增加数据水平结构信息，能够取得更好的估测结果。同时，本研究还评估了筛选变量对森林蓄积量估测的影响，结果表明，虽然通过变量筛选能够降低参数数量，由原来的24个减少至7个，可极大提高运算效率，但R2未变化，RMSE从36.23 m3·hm-2升至36.50 m3·hm-2，rRMSE从31.92%升至32.97%，MAE从26.16 m3·hm-2降至26.08 m3·hm-2，MRE从38.35%降至38.05%，说明经变量筛选后，模型精度虽有变化，但是差别不大，可直接用筛选后的变量进行建模。因此，处理区域大尺度问题时，在数据量大或运算能力不足的情况下，建议使用筛选变量建模，这样可在稍微牺牲精度的情况下尽可能缩短计算时间。

6 结论

本研究基于机载激光雷达点云数据提取的森林高度参数和郁闭度，结合分层地面样地调查数据，采用随机森林算法构建森林蓄积量估测模型，结果表明，增加林分郁闭度信息可显著提高森林蓄积量估测精度。通过变量筛选，虽然能够降低参数数量，但对模型精度具有一定影响。在建模精度要求较高的情况下，建议使用全变量进行蓄积量估测； 而在数据量较大的情况下，建议使用筛选变量进行蓄积量估测。基于机载激光雷达点云数据估测森林蓄积量显著优于光学遥感数据，可为森林蓄积量高效准确估测提供方法依据，能够满足大范围森林蓄积量快速反演需求。