基于深度神经网络的DFIG低电压穿越技术研究

余欣梅，陈豪君，王星华

（1.中国能源建设集团广东省电力设计研究院有限公司，广州510663；2.广东工业大学自动化学院，广州510006）

低电压穿越技术是保障电网故障过程中风机和电网安全的重要手段。目前DFIG双馈风机的低电压控制基本分为改进控制策略和增设硬件电路两类：文献［1-2］采用带补偿项的矢量控制加速定子磁链暂态分量衰减实现低电压穿越，但受变流器容量限制，仅适用于轻度故障。文献［3］增设撬棒电阻并推导其整定方法，适用于严重故障，但在投入过程中双馈风机会大量吸收无功，不利于电网电压稳定。文献［4］理论分析了多种低电压穿越技术，讨论了DFIG控制系统的PI参数选择对DFIG机组LVRT效果的影响。

为取得更好的控制性能，有学者提出用遗传算法［5-6］、粒子群［7-8］等智能算法［9-10］对PI控制器参数进行优化。这类优化方法均为电网故障后根据当前故障情况进行参数优化，但普遍存在两个问题：（1）在实际情况下，故障的暂态过程比较快，故障后优化很可能会错过抑制暂态量的最好时刻；（2）在有限的时间内在线优化难以同时满足速度和准确度上的要求，严重制约了其在高实时性领域上的应用，实际意义不大。

针对以上不足，本文结合人工智能思想，提出将深度学习算法应用于双馈风机的LVRT的实时优化控制。首先通过PSCAD-MATLAB联合调用技术对风机故障过程进行大量仿真，并利用粒子群优化算法对相应的控制参数进行离线优化，并根据故障程度进行分类，从而形成不同故障程度的优化控制策略参数表。其次建立DNN故障程度识别模型，将仿真算例形成训练集，以故障信息作为训练样本的输入参数对故障程度进行分类训练。训练成功的网络即构成控制策略优选模块，只需输入所采集的故障信息即可实时选择并确定优化的LVRT控制策略和参数，从而解决了实际故障时控制的实时性问题。

1 低电压穿越策略以及参数优化

1.1 PSCAD与MATLAB的联合调用

故障点与DFIG并网点的距离直接影响并网点电压的跌落深度。根据电压跌落深度可将故障程度分成三种：轻度故障（跌落10%～30%）、中度故障（跌落30%～50%）和严重故障（跌落50%～80%）。不同的严重程度决定了机组应采取的LVRT策略、控制目标和优化参数，本文利用粒子群优化算法进行不同控制策略的选择和参数优化，并基于PSCAD-MATLAB联合仿真进行的电磁暂态和优化过程的仿真，联合仿真模块如图1所示。

图1中，PSCAD中建立含DFIG的仿真网络进行故障仿真，Matlab中利用Multiple Run进行PSO寻优，两者通过文件进行优化参数和适应度数据的交互。仿真网络和参数参见文献［11］及本文2.2节。

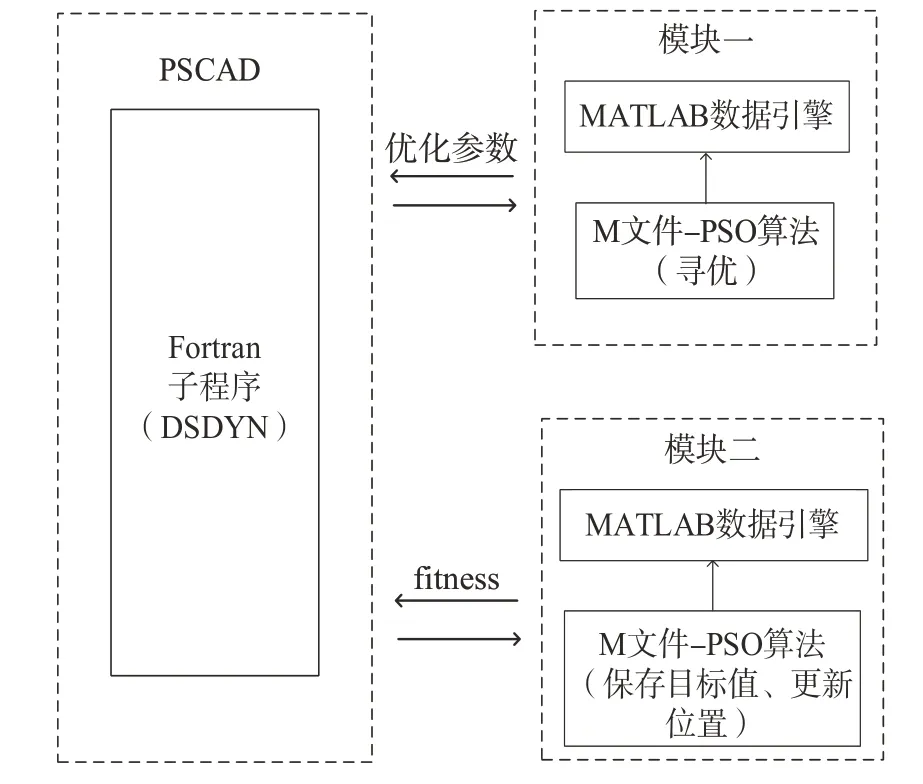
图1 联合模块示意图Fig.1 Illustration of combined model

1.2 LVRT策略选择和优化过程

如前文所述，不同故障程度须选择不同的LVRT策略及相应的优化控制参数。

1）改进控制策略参数优化

如图2，转子侧变流器采用了控制外环为功率环，控制内环为电流环的双闭环控制系统，当要求电流内环具有较快的电流跟随性能时，可按典型I型系统设计，从而得到PI控制器参数的整定公式［12-13］：

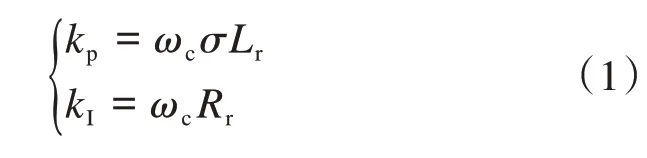
式中：σ=1-L2m( LsLr)；Rr和Ls、Lr分别为转子电阻（Ω）和定、转子电感（H）；Lm为励磁电感（H）；ωc=2πfc，fc为截止频率（HZ）。一般要保证截止频率在等效开关频率的1/10以内。

故障后闭锁控制外环，只需考虑内环PI调节器的运行特性。由于d、q轴电流环结构相同，PI参数设置相同，通过式（1）计算和多次仿真调整后得到初始值。

故障点较远时，硬件设备不动作，转子侧采取改进的控制策略，在电流环给定值上添加定子磁链波动的补偿项，内环d、q的指令值变为［2］：

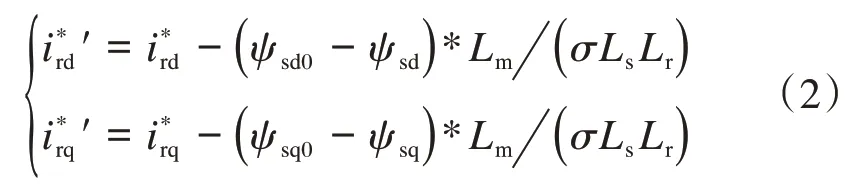
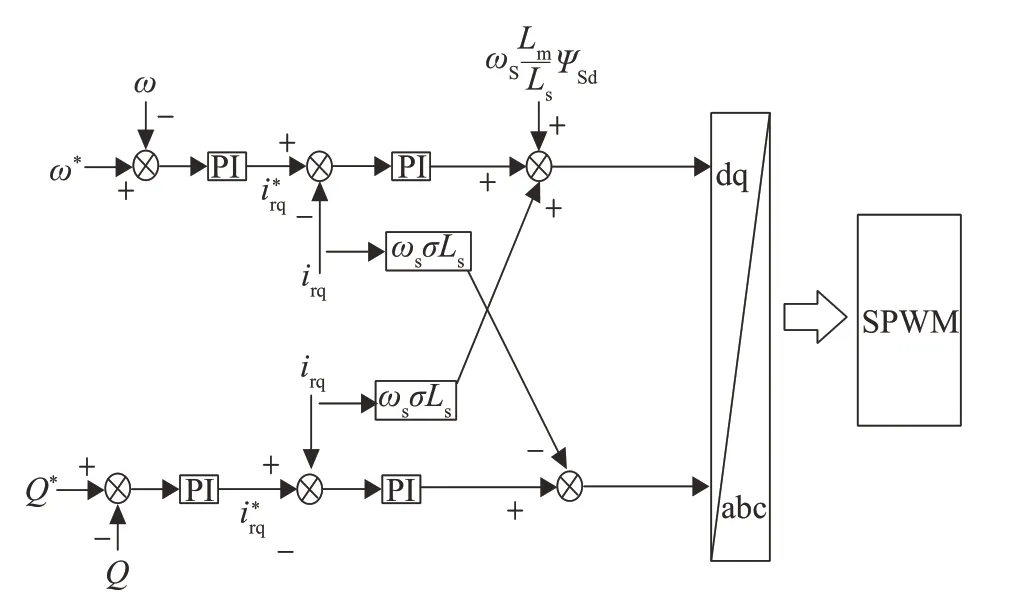
图2 转子侧变流器控制框图Fig.2 Schematic diagram

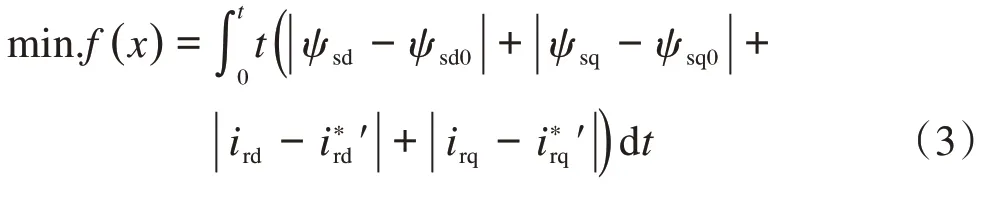
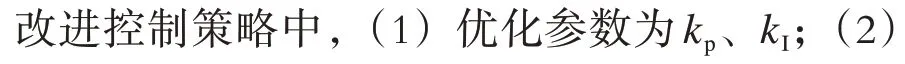
通过PSCAD/EMTDC仿真DFIG低电压穿越电磁暂态过程［14-15］，t=8 s时，电网发生三相短路故障，8.2 s故障切除，再利用Matlab中的Multiple Run模块联合仿真粒子群优化过程，优化的种群规模30，迭代终止条件为最大迭代40次及适应度无变化。

在文献［11］中的仿真网络中设置故障参数进行仿真，在电压跌落20%以内时，优化前后转子电流内环PI参数如表1所示。

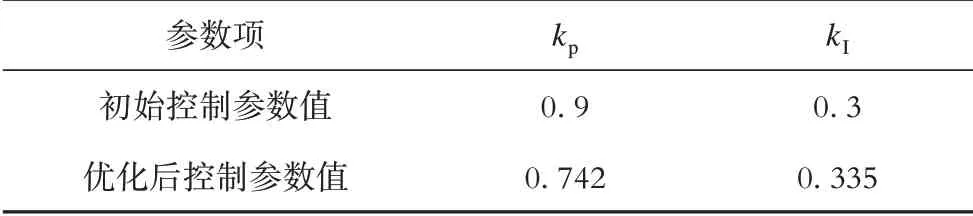
表1 PI控制器参数对比Tab.1 Comparison of PIparameters

比较传统控制、原始参数改进控制和优化参数改进控制三种方案的仿真结果，如图3所示。

对比图3发现，加入转子电流补偿量的改进控制可使暂态分量在半隔周波后快速衰减，机组暂态波动更快稳定。而在参数优化的改进控制中，转子电流峰值，定子磁链变化幅度均较未优化前更小，输出无功更多。

2）撬棒保护参数优化

严重故障下，改进控制策略受DFIG变流器容量约束难以发挥作用，需根据故障情况投入不同的撬棒电阻实现低电压穿越。可变电阻撬棒电路拓扑结构如图4所示。

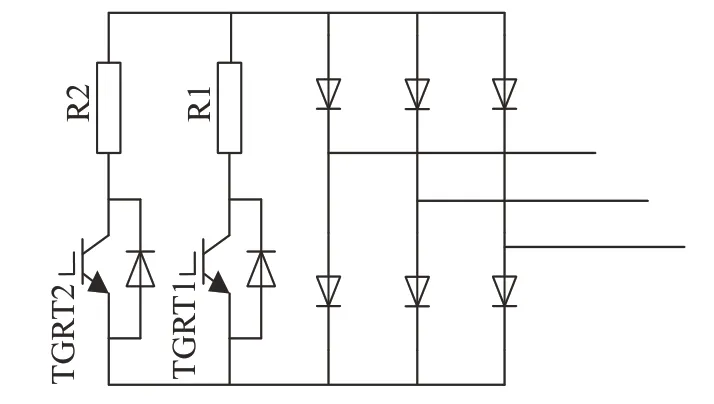
图4 撬棒电路的拓扑结构Fig.4 Topology of crowbar circuit

表2 优化前后撬棒阻值对比Tab.2 Comparison of Crowbar crowbar resistance

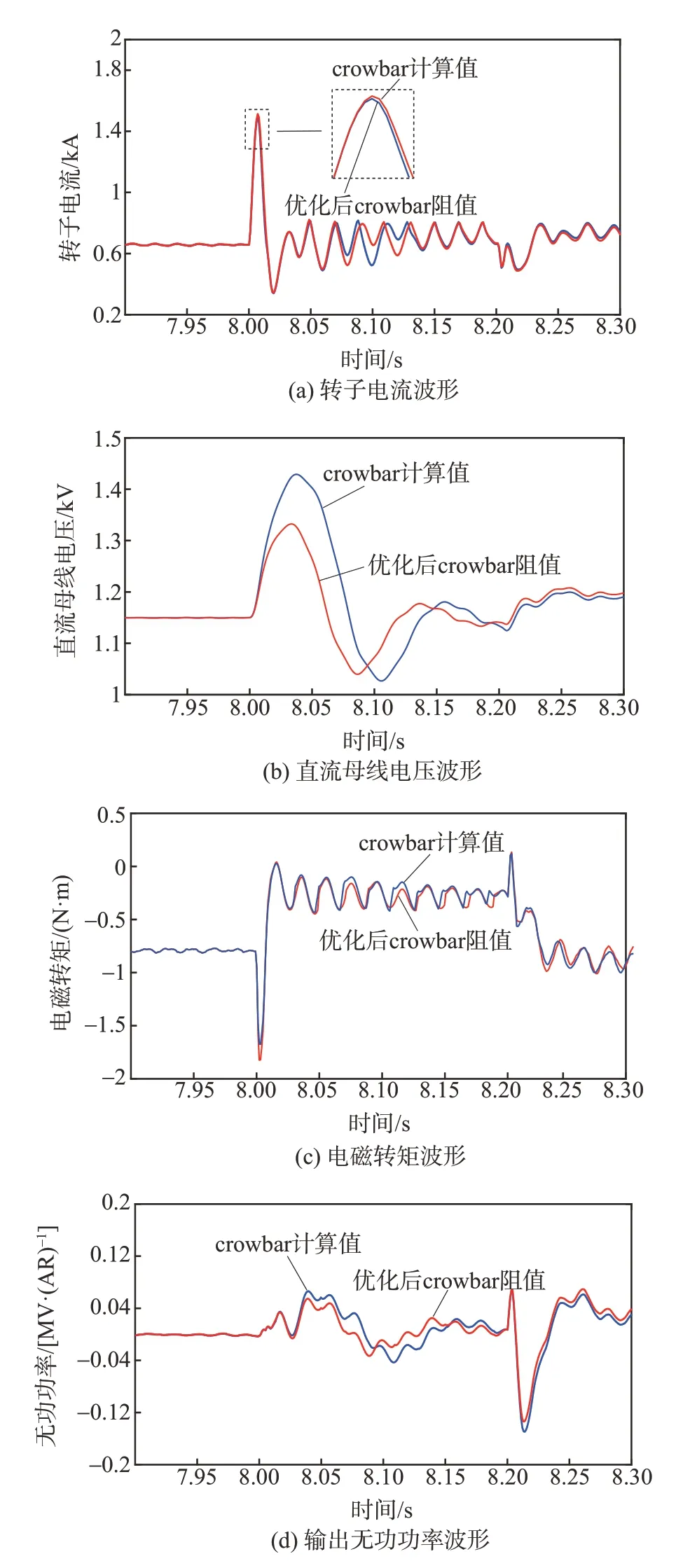
图5 电压跌落70%场景的LVRT特性对比Fig.5 Comparison of LVRT characteristics

两种方案的电磁转矩和无功消耗差异不大，但固定电阻方案波动大，对机组安全更为不利。

3）联合控制参数优化

中度故障下，单独采用改进控制策略效果不明显，无法降低转子电流峰值；纯撬棒保护能有效抑制过电流和过电压，但撬棒电路投入越久，机组从电网中吸收的无功会更多。

利用撬棒保护和改进控制结合的控制策略，能够有效解决两种方案单独投入时存在的弊端：在转子侧过电流严重时投入撬棒电路，旁路转子侧变流器，当电流恢复到改进控制的可控范围内切出撬棒电路，采用变流器改进控制策略，直到故障结束。

本文通过设置电流门槛值来制定两者的切换规则，规则如下式所示：

式中：i→r为转子电流（A）；IrN为转子电流额定值（A）。

同样，对电压跌落50%时的电流内环PI控制器和IGBT开关占空比进行优化，得到参数如表3所示。

闻喜县经济社会用水户数量较大，部分用水户担心用水量调查触及自身利益，不能积极配合调查工作，导致调查工作难度加大；规模以下典型用水户，由于水量计量设施尚未普及，一部分用水户没有计量设施，用水量数据获取困难。台账建立前需进行大量的清查工作及经济社会用水调查对象样本名录的核实确认，台账建立时间紧、困难大。

表3 最优控制参数Tab.3 Optimal control parameters

图6为在电压跌落50%的情况下三种方案的LVRT特性对比，其中联合控制的电流门槛值设为0.8 kA，切换规则按式（7）执行。

联合控制策略灵活运用两种方案，有效减少了撬棒电阻投入时间和次数，同时在抑制电流电压能力上与纯撬棒相近，因此适用中度的电压跌落情况。

根据上述优化结果形成参数表，用于DNN网络识别故障后匹配策略和参数，具体参数如表4所示。

每种故障程度都有对应的LVRT策略，当程度较轻时，只采取改进控制策略，参数给的是转子控制系统内环的PI值；而中度故障下，采用联合控制策略，则参数涉及PI值和撬棒阻值；严重故障下单独投入撬棒电路，因此只给出撬棒阻值。

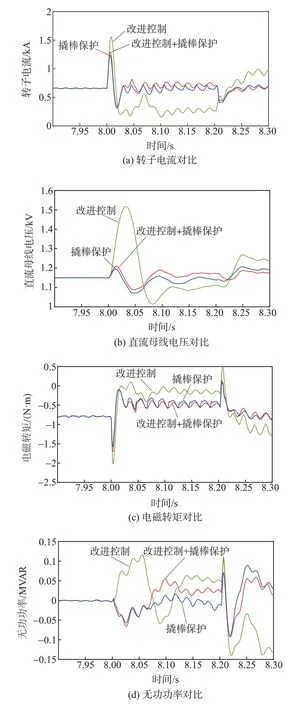
图6 风机LVRT在电压跌落50%时的特性Fig.6 LVRT characteristics with 50%voltage sag

2 故障程度识别模型

2.1 DNN结构与原理

DNN本质上是一个包含多个隐含层的前馈神经网络，是近年来发展迅速的深度学习网络的一种，具有很好的非线性映射关系和学习能力，适宜处理更大的函数集合［16-18］，结构如图7所示：

表4 策略参数表Tab.4 Parameter table

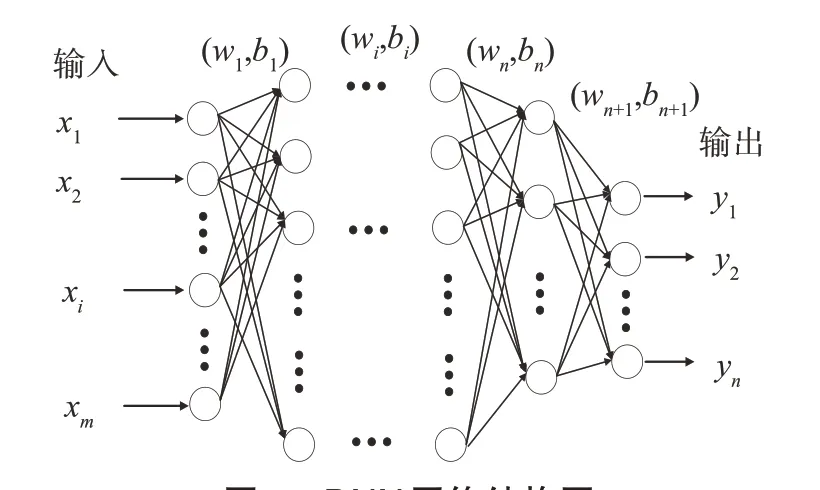
图7 DNN网络结构图Fig.7 Structure of DNN

x1，x2，…xn为模型输入，是由故障信息中提取的定、转子电流所组成的向量，输入层采用线性恒等函数作为激活函数，隐含层层数为n，最终传递给网络的输出向量y1，y2，…xn。(wi，bi)分别为第i个隐含层的权重与偏置。假定第i-1隐含层的输入向量为：

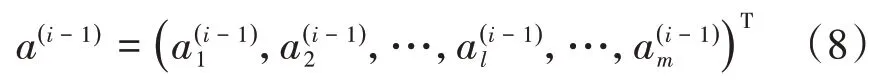
则第i层神经元的输出向量a(l)可表示为：

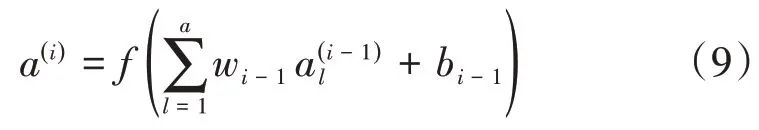
式中：a为第i层神经元数目；w i-1、bi-1为第i-1层的权重矩阵和阈值变量，f(x)采用ReLU函数。

在分类问题中，常用softmax分类方法，将多分类的输出值转化为相对概率，如式（10）所示：

式中：i为类别索引；C为总类别数；Vi是分类器前级输出单元输出；Si为当前元素与所有元素的指数和的比值。

输入通过softmax函数计算完后，再计算它们的交叉熵，表示的是目标实际输出概率与期望输出概率的差距，表达式为：

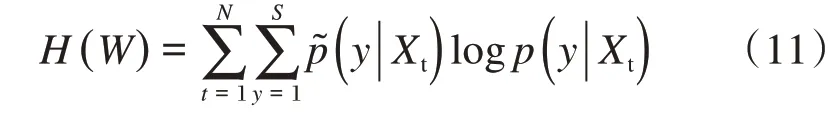
式中：N为训练样本的数目；p~(y|Xt)为期望概率，值为0或1；p(y|Xt)为DNN网络的实际输出概率。

最后，由式（9）可求得整个网络输出为：

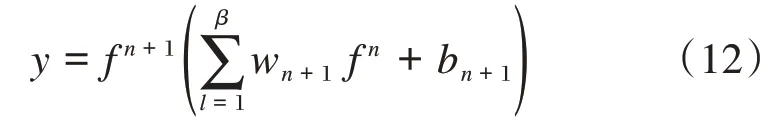
其中：最后一层隐含层神经元数量为β；f n为计算的最后一层隐含层输出；wn+1、bn+1为输出层权值和偏置。

2.2 训练样本集与测试样本集数据生成

在PSCAD/EMTDC上建立双馈风机-无穷大系统，图8为仿真系统原理图。

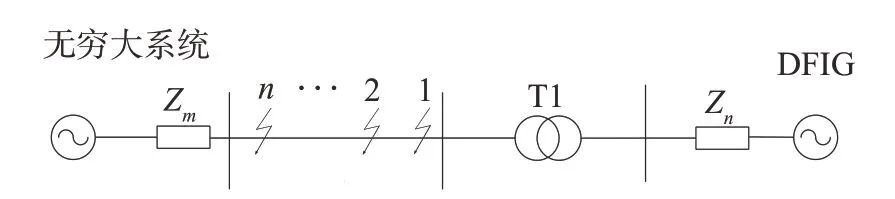
图8 仿真系统图Fig.8 Diagram of simulation system

模型参数：DFIG容量为2 MW；T1表示风机经0.69 kV/33 kV和35 kV/110 kV两个变压器并入无穷大电网；线路长度L取50 km；n为不同的故障点序号。

为方便研究，本文只考虑了三相短路故障的情况，仿真不同故障点和过渡电阻下DFIG的故障暂态过程，选取故障发生后一个周波的三相定、转子电流采样数据（每周波的采样点数为24），构成DNN的训练集和测试集，仿真参数如表5～表6所示。

表5 训练样本仿真参数设置Tab.5 Simulation parameters for training set

表6 测试样本仿真参数设置表Tab.6 Simulation parameters for testing set

表中，故障位置指故障点离风机并网点的距离，从0～50 km中选取了10个故障点，体现了故障点的远、中、近，与故障程度相对应；同理，考虑存在过渡电阻的情况，一共设置了9个阻值。故障程度根据电压跌落设置轻度、中度和严重故障三种，DNN的标签即为相应故障类型下的优化控制参数。

2.3 仿真结果

DNN的分类效果受网络参数的影响很大，仿真中中设置了不同的DNN网络结构、参数以及迭代次数，并利用测试集校验训练结果，如表7所示。

表7 不同网络参数下DNN故障识别仿真结果Tab.7 Results of simulation

由表7分析可知，DNN的隐含层层数、各层神经元个数、迭代次数等均会影响训练的精度、时间。参数序号1、2的对比表明，隐含层的层数越多，越能够有效识别特征来对事物进行区分，获得更好的分类效果；序号1、3的对比表明学习率过大，难以避免出现训练震荡的问题，使得达到相同测试准确率的时间更长；对比序号1、4，隐含层层数相同，迭代次数相同，神经元数量能够提升准确率，但是太高容易出现过拟合现象；序号4、5网络结构相同，迭代次数越多准确率越高。此外，测试过程中，所有训练好的模型在输入参数后0.2～0.4 ms的时间内，均能够获取相应的优化控制参数，能够满足实时控制的需要。

图9为序号1、2、3的训练图，其中括平均训练误差和测试准确率。

综合分析结果，在测试样本中故障位置、过渡电阻等参数均不同的情况下，DNN仍然能准确判断故障程度，这是因为DNN具有很强的泛化能力与学习能力，当样本数足够时，对网络的输入向量进行反复多重的训练可以实现更好的效果，使得该网络用于故障程度识别具有极高的准确率。

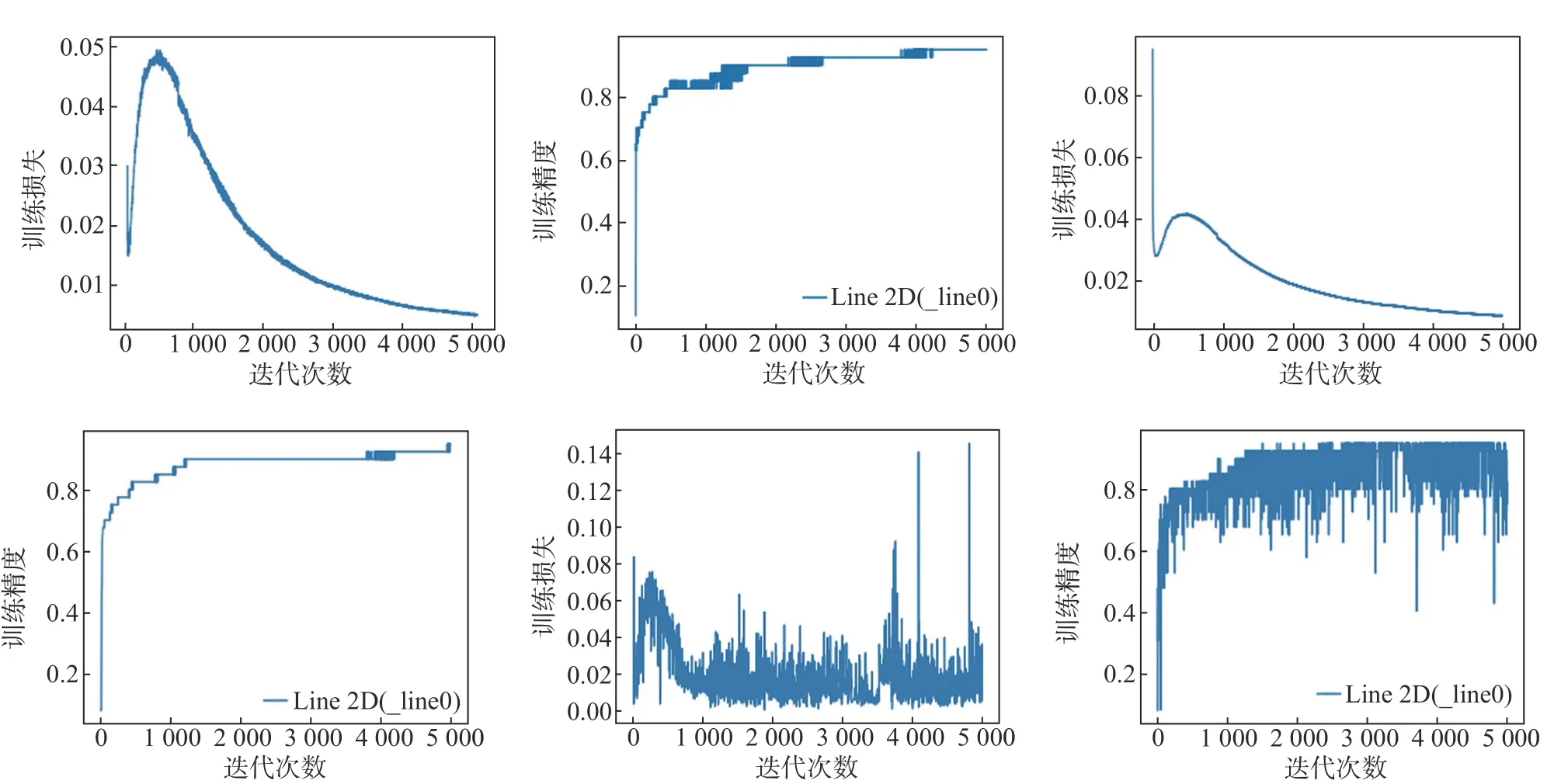
图9 训练结果图Fig.9 Graphic of training result

3 结论

由于无法提前预知电网故障，优化控制在实时性上无法满足LVRT的控制要求，本文提出将控制参数离线优化，提前考虑所有的故障情况，并制定成一个策略参数表。通过建立DNN网络来进行故障识别，在面对各种故障状态下均可直接从表中选取控制策略和参数。本文基于深度神经网络的低电压穿越方案在一定程度上克服了传统参数优化无法满足实时控制要求的问题，有效改善了DFIG机组的低电压穿越效果。