基于小波分解的集卡港内周转时间预测

孙世超 董曜 李娜 郑勇

摘要：為准确预测集卡的港内周转时间，进而提升整个物流系统的作业效率，通过对集装箱码头闸口数据进行深入分析，得到3种不同任务类型的集卡港内周转时间序列，并在此基础上提出一种基于小波分解和自回归移动平均（autoregressive moving average， ARMA）模型的集卡港内周转时间预测方法。该方法首先利用小波分解技术对集卡港内周转时间序列的多维变化特征进行逐层分离，再利用ARMA模型对分离后的多个时间序列分别进行拟合，然后对拟合结果进行合并，以此近似模拟原序列的时变规律，继而实现集卡港内周转时间的短期预测。为验证该方法的有效性，将数据样本划分为训练集（75%）和测试集（25%），训练集用于拟合多维ARMA模型，测试集用于检验ARMA模型的预测结果误差。研究结果表明，对于3种任务类型，该模型均可以精确预测集卡的港内周转时间，为物流企业调整集卡运输计划提供相应的技术支持。

关键词：  水运管理; 集卡周转时间预测; 小波分解; 自回归移动平均（ARMA）模型; 码头闸口数据

中图分类号：  U691+.3

文献标志码：  A

收稿日期： 2021-03-25

修回日期： 2021-06-21

基金项目： 国家自然科学基金（71702019）

作者简介：

孙世超（1988—），男，辽宁大连人，副教授，博士，研究方向为交通运输工程，（E-mail）dlmu_sunshichao@163.com

Meeting of the Waterborne Transport Division， World Transport Convention 2021 （WTC 2021）

Truck turnaround time prediction in a port based on wavelet decomposition

SUN Shichao， DONG Yao， LI Na， ZHENG Yong

（College of Transportation Engineering， Dalian Maritime University， Dalian 116026， Liaoning， China）

Abstract： In order to accurately predict the in-a-port turnaround time of trucks and improve operation efficiency of the whole logistics system， three different task types of in-a-port turnaround time series of trucks are obtained through the analysis on the gate data of container terminals. On this basis， a method for predicting the in-a-port turnaround time of trucks based on the wavelet decomposition and the autoregressive moving average （ARMA） model is proposed. This method initially employs the wavelet decomposition technology to separate the multi-dimensional change characteristics of the in-a-port turnaround time series of trucks， and then applies the ARMA model to fit the time series after separation， respectively. Subsequently， the fitted results are merged to simulate approximately the time-varying law of the original series， and then realize the short-term prediction of the in-a-port turnaround time of trucks. In order to verify the effectiveness of the method， this study divides the data sample into a training set （75%） and a test set （25%）. The training set is used to fit the multi-dimensional ARMA model， and the test set is used to test the prediction error of the ARMA model. The results show that for the three task types， the model can accurately predict the in-a-port turnaround time of trucks， and it can provide corresponding technical support for the adjustment of truck transportation plan of logistics enterprises.

Key words： water transportation management; prediction of truck turnaround time; wavelet decomposition; autoregressive moving average （ARMA） model; terminal gate data

0 引 言

随着外贸经济的不断发展，近些年我国几个主要港口的集装箱吞吐量增长迅速，如深圳盐田港的集装箱吞吐量已连续三年突破1 400万TEU。在此背景下，提高港口的现代化管理水平，提升集装箱码头设备的作业效率，减少集卡的周转时间，成为推动我国港口绿色化和智慧化发展需关注的重要领域之一。具体来说，集卡在港内的周转时间受港口全天的集卡到达分布影响较大，当大量集卡到达港口时就会出现排队现象，这一时段集卡的平均周转时间就会增加。为解决集卡到达分布不均的问题，港口管理者可以通过集卡预约方式主动调整每一时段集卡的到达数量[1]，还可以通过向集卡公司或物流公司发布当前的作业排队情况以及未来短期内周转时间的预测结果来引导其合理安排运输计划。相比之下，后者的快速响应能力（准备周期较短）和易实施性（不需要制定详细方案，只需要发布信息）更好，可以作为从随机到达模式过渡到集卡预约模式的管理手段，更适应我国当前港口智慧化发展的阶段性需求。

然而，由于港内作业流程较为复杂，且集卡作业效率受到多种因素的影响，集卡周转时间存在一定的波动性和不确定性。因此，准确把握集卡周转时间的变化规律，精确模拟并量化其发展趋势特征，是实现集卡周转时间预测的关键。一些研究将最小化集卡周转时间作为港口内部协同调度优化的目标函数，通过构建并求解相应的理论优化模型，揭示港内作业规则及方案（一般涉及多个对象的协同调度，如集卡调度方案、作业设备调度方案、集装箱堆存方案等）与集卡周转时间预测值之间的因果关系[1-3]。然而，这些研究通常是站在港口管理者的角度提供最优化的码头作业调度策略和资源配置方案（系统最优）[4-5]，而不是站在物流企业或集卡公司的角度寻求企业自身的集卡作业成本最小化。因此，有别于以往的研究，本文从企业用户最优的角度研究集卡周转时间的预测方法，通过对集卡周转时间进行更加精准的预测与信息发布，引导物流企业或集卡公司合理安排运输计划，减少企业自身成本。

此外，在系统最优研究中，集卡周转时间的模拟过程往往涉及多个子目标函数以及多个物理过程[6]，这一方面会导致此类模型的精确求解变得困难，另一方面，理论优化模型往往依赖于一些经验假设[7]，但大部分假設的合理性面临着缺乏实际数据而无法进一步验证的问题，故不能保证所模拟的集卡周转时间变化规律的准确性。为避免上述问题，本文尝试从数据挖掘的角度，利用所采集的码头闸口数据，提出多任务类型的集卡周转时间预测方法。然而，国内外鲜有这方面的研究成果。大量基于数据挖掘方法进行短期预测的研究都集中在城市道路交通领域，其主要思路是根据过去的交通数据信息，结合数据挖掘方法，预测未来短时间内该区域的交通变化情况，相关的研究方法相当成熟且丰富。其中，小波分解算法作为20世纪80年代数学界的重要研究成果，因其具有良好的分离和去噪能力以及时频域局部化能力受到了研究人员的青睐，将小波分解算法与其他模型进行结合往往能大幅提高预测的精度。PINEDA等[8]通过小波分解算法提取交通网络特征，并将提取的特征作为神经网络的输入对交通客流量进行预测。FU等[9]利用小波分解算法分离原始序列，结合自回归移动平均（autoregressive moving average， ARMA）模型和神经网络预测短期的道路行程时间。

鉴于小波分解算法和ARMA模型在道路交通变化短期预测中得到了有效且广泛的应用，本文利用深圳某港口的集装箱码头闸口数据，获取不同任务类型的集卡平均周转时间序列，并提出一种基于小波分解的集卡周转时间预测方法，通过量化时间序列的长期变化趋势和短期波动规律，最终实现集卡周转时间预测，并通过实例证明其有效性。

1 数据准备与处理

1.1 数据准备

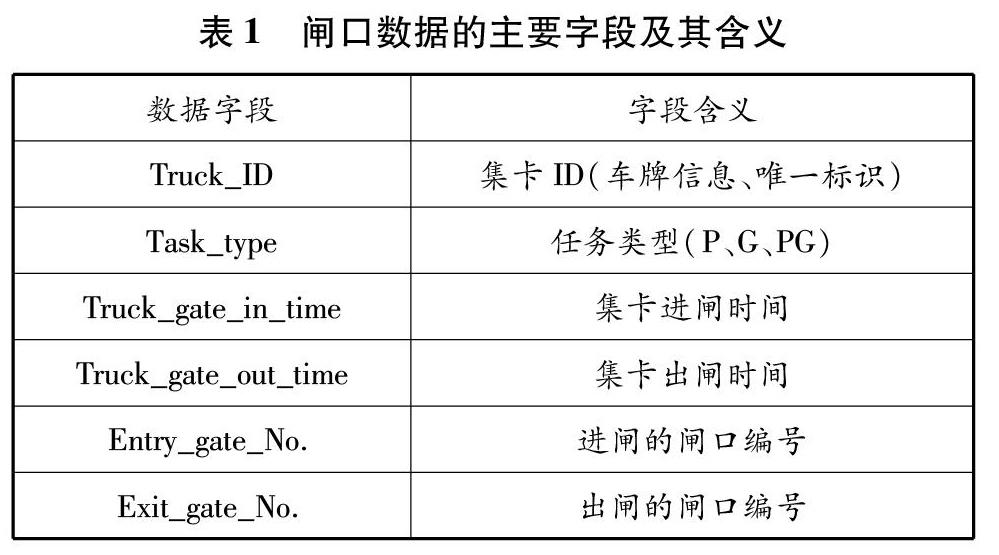
本研究所使用的数据为深圳市某港口集装箱码头2018年11月5日至12月2日（4个自然周，共计28天）的闸口数据，共约29万条记录。该数据主要记录了每辆集卡进出码头的具体时间、闸口位置和任务类型（见表1），其中任务类型包括3种，即提箱任务（P）、交箱任务（G）和一交一提任务（PG）。

1.2 数据处理

根据上述数据所包含的集卡进出闸口时间，能够精确计算每辆集卡在港内的周转时间，并可以按照不同任务类型进行统计。因此，本研究将一天划分为96个时段（每个时段15 min），计算每个时段不同任务类型的集卡平均周转时间，计算步骤如下：

步骤1 根据原始数据提供的集卡实际进闸时间，获取每个时段的进港集卡数量，并按照任务类型进行分组。

步骤2 根据每个分组内集卡的进出闸口时间，计算每个分组内的集卡平均周转时间，计算方法如下：

Twt=Nwti=1（Toutwti-Tinwti）/Nwt

（1）

式中：Nwt和Twt分别为在时段t进入码头且任务类型为w的集卡的数量和平均周转时间;Toutwti和Tinwti分别为在时段t进入码头且任务类型为w的第i辆集卡的出闸和进闸时间。

1.3 数据特征

将上述获取的Twt用时间序列图表示（图1），其中横轴代表时段序号，共2 688个时段。从图1可以看出，3个时间序列总体上存在着以自然周为单位的周期性变化，但在短期内仍具有很强的波动性。事实上，在实际的集装箱码头作业过程中集卡周转时间受到许多因素的影响，有些因素会导致短期内集卡周转时间的不确定性增大（如天气原因、海况变化、码头施工、设备故障等），而有些因素决定了集卡周转时间的周期性变化特征（船期、集卡到达规律等）。因此，尝试使用若干组特征方程近似表征各种因素对集卡平均周转时间的影响，模拟时间序列的长期规律性变化，以及描述时间序列的中短期随机变化特征。

2 研究思路与研究方法

2.1 研究思路

假设3种任务类型的集卡平均周转时间序列为受到多种因素影响的随机序列，先采用小波分解算法对相应的时间序列进行分解，得到不同维度的信息特征（多个时间序列），再通过ARMA模型对分离后的多个时间序列分别进行拟合、还原和合并，用来模拟原序列的变化规律，最终实现对未来时段集卡周转时间的短期预测，见图2。

具体来说，小波分解算法可以依据时间序列变化频率的快慢，将其分解为高频信号和低频信号，以此分离原数据不同维度的信息特征。其中，低频信号通常蕴含趋势序列信息（在一段时间内较为稳定且影响力较强的特征），而高频信号则包含着随机序列信息（变化比较剧烈且影响力相对较弱，这类信息往往会被认为是噪声或者是随机项）。因此，所研究的3种时间序列所包含的趋势序列信息可以被认为受一些较为固定和长期因素的影响，例如堆场的作业规则与效率、集卡到达规律等，而相应的随机序列信息则受到变化较为剧烈的短期因素的影响，例如当日天气、海况因素等。因为原序列均为平稳序列（通过单位根检验），所以分离后得到的低频信号序列和高频信号序列也都是平稳序列，可利用ARMA模型对分离后的多个时间序列进行拟合。

2.2 研究方法

2.2.1 小波分解和Mallat算法

小波分解是一种可以实现时频域局部化的分析方法，它可以通过拉伸和平移运算细化信号（函数）。与傅里叶变换不同，小波函数具有衰减性，这使得小波函数可以克服傅里叶变换无法局部化的缺点，从而对原函数信号突变部分进行分析。本文采用正交离散小波分解算法，其最大的优点是可以将原函数投影到正交小波基上使得投影后的信号没有冗余。具体来说，小波分解的结果wf可以通过以下的卷积公式获得：

wf（a，b）=∫+∞-∞a-1ψ（（x-b）/a）f（x）dx

（2）

∫+∞-∞a-1ψ（（x-b）/a）dx=1

（3）

式中：f（x）为原函数;ψ（x）为小波函数;a为尺度系数，决定了小波分析的精度，a越小，小波分析的精度就越高;b决定了对函数进行小波分析的位置。该算法通过对a的离散取值，将原函数映射到一个正交空间V，再将其进一步分解为Vj（低频空间）和Wj（高频空间）。上述将低频信号与高频信号分离的过程可以通过Mallat算法实现，其原理为：通过上一层分解得到的低频信号可被继续分解为低频信号和高频信号，这样就可以将原函数在不同时频层次上的特征分离出来，然后通过小波逆變换还原信号。公式如下

Aj+1=GAj

（4）

Dj+1=HAj

（5）

Aj=G*Aj+1+H*Dj+1

（6）

式中：Aj+1和Dj+1分别为经第j+1层滤波后的尺度系数和小波系数;Aj为经第j层滤波后的尺度系数;G和H分别为低通滤波器信号和高通滤波器信号;G*和H*分别为可逆低通滤波器信号和可逆高通滤波器信号。

2.2.2 ARMA模型

对于平稳序列，通常采用ARMA模型解释先前的自我变化和当前的外部干扰对时间序列的影响。ARMA模型结合了自回归（autoregressive， AR）模型和移动平均（moving average， MA）模型的优点。ARMA（p，q）模型的一般形式可以表示为

Yt=pk=1（kYt-k）+qs=0（θsεt-s），

εt-s∈（0，δ2）

（7）

pi=1（θizi）=-1

（8）

式中：Yt为时间序列在t时刻的取值;εt-s为一个独立的白噪声序列，它与所有的Yt都无关;k和θs分别为AR和MA模型的参数;δ2为高斯白噪声的方差;z为特征多项式的解。

ARMA模型参数p和q的选取步骤如下：计算该时间序列的自相关系数和偏自相关系数;通过序列的拖尾或截尾找出p和q的大致范围;在给定的范围中寻找p和q并进行拟合，得到多组拟合的结果，根据结果的拟合优度R2（反映因变量的全部变化可以通过回归关系由自变量所解释的比例，该值越大，拟合结果越好）、AIC准则和回归误差来选择p和q。

3 结果分析

3.1 小波分解结果

利用上述小波分解算法对3种时间序列进行多层分解，结果见图3～5。以PG为例，图3分别给出每层分离出的低频信号序列（图3a）和高频信号序列（图3b）。总体看，随着小波分解层数的增加，由尺度系数逆变换得到的低频信号越来越平滑，而高频信号越来越复杂;当分解层数超过5层时，分离出的低频信号的平滑效果并不明显。由于当前没有确定小波分解层数的统一准则，所以将尝试1到5层的所有可能，将分离出的低频和高频信号由不同的ARMA模型进行拟合。

3.2 ARMA模型拟合结果

为验证小波分解对集卡平均周转时间预测精度的提升作用，将分解层数为0（即将原数据直接进行ARMA模型拟合）得到的结果作为参照组，其余分解层数所对应的拟合结果作为实验组。为保证模型的鲁棒性，将时间序列前3周共计2 016个时段的数据作为训练集来拟合模型，将时间序列最后一周共672个时间段的数据作为测试集来验证模型的泛化能力。引入均方根误差eRMS和平均百分比绝对误差eMAP来衡量模型拟合结果的好坏：

eRMS=ni=1（xi-x*i）2/n

（9）

eMAP=ni=1xi-x*i/xi/n

（10）

式中：xi为实际值，x*i为模型拟合值。

基于小波分解的ARMA模型的具体训练与测试过程如下：

步骤1 k为小波分解层数（初始值为1），判断当前分解层数k是否大于4。若k≤4，则对原序列进行k层小波分解，得到1组低频信号和k组高频信号;若k>4，则结束流程。

步骤2 将上述分解后得到的时间序列分为训练集和测试集（每一序列的前三周为训练集，最后一周为测试集），利用训练集分别拟合低频信号和高频信号的ARMA模型。

步骤3 利用拟合得到的多个ARMA模型进行预测，并将低频信号与高频信号的预测结果进行合并，再与测试集中的真实值进行比较，计算预测误差。

步骤4 k=k+1，循环步骤1～4，直到流程结束。

基于小波分解的ARMA模型预测流程见图6。

3种任务类型的集卡平均周转时间预测误差分析见表2。其中， “低频信号测试误差”为低频信号的预测结果与真实值之差;“高频信号测试误差”是对当前层数分解后得到的多个高频时间序列分别建立ARMA模型并进行预测，再将合并后的预测结果与真实值进行比较，最终得到的测试误差;“总体测试误差”为低频信号与高频信号的预测结果合并所得的结果与真实值之差。

表2结果表明，随着小波分解层数的增加，3种任务时间序列的低频信号和高频信号的测试误差都在逐步减小，这是因为随着小波分解层数的增加，时间序列在不同尺度下的变化特征会得到越来越精细化的描述，分离得到的特征曲线也会变得更加平滑，使得ARMA模型更容易有效地模拟其变化规律。3种任务时间序列总体测试误差均在小波分解层数为2时达到最小。因此，可以认为小波分解层数为2时，ARMA模型的预测精度是最高的。具体而言，集卡平均周转时间受到许多因素的影响，这些因素大致可以分为偶然因素和较为稳定的因素，小波分解的目的就是分离时间序列中受随机因素影响（天气、海况、车/船延误、机械故障等）而产生的噪声项，即经过2层滤波后的高频信号部分，而剩下的低频信号则反映了由码头布局、集卡到达分布等因素所共同决定的集卡平均周转时间变化的长期规律。

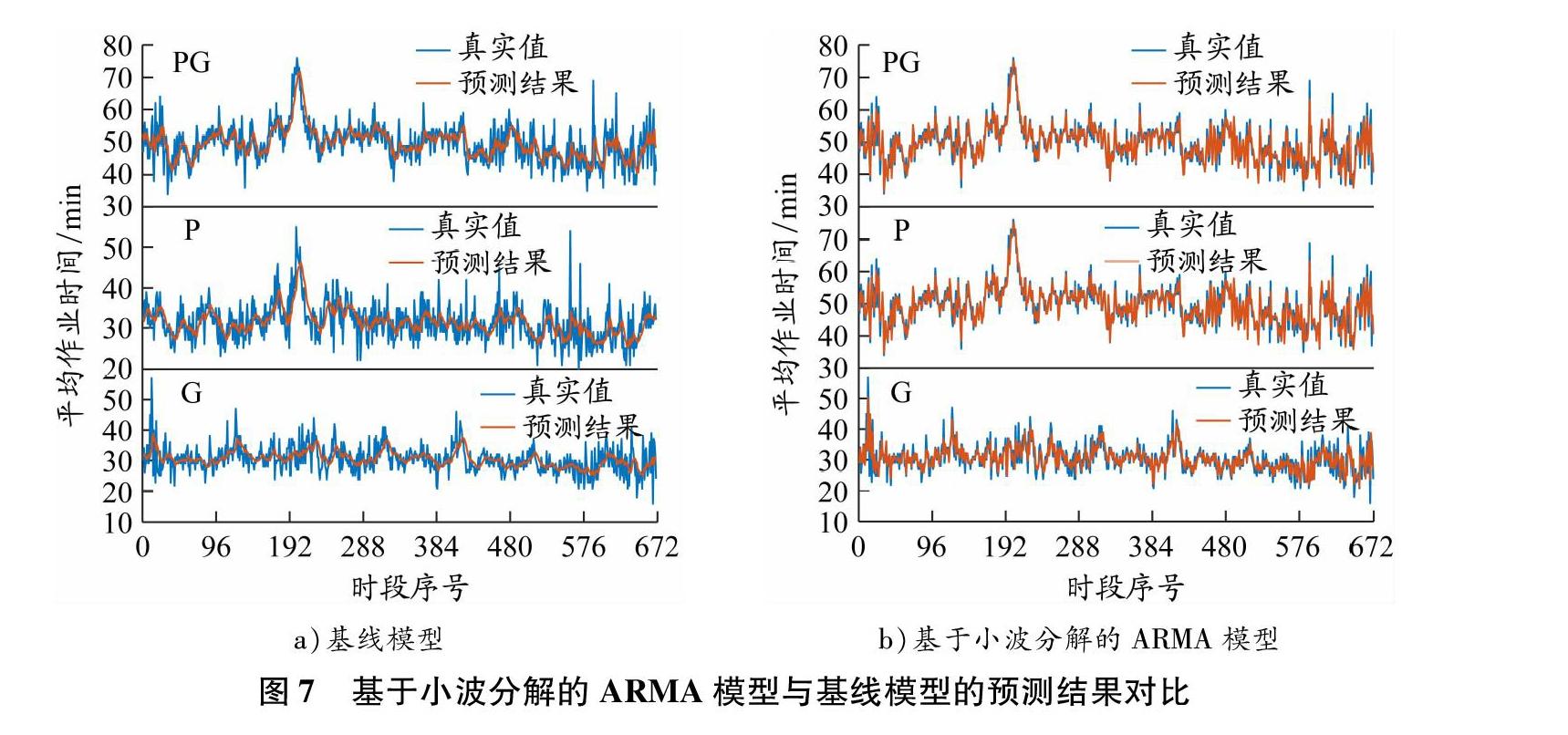
此外，为更加直观地体现小波分解在集卡周转时间预测精度方面的提升作用，图7分别给出了基于原始时间序列拟合的ARMA模型的预测结果（分解层数为0，基线模型），以及基于小波分解（分解层数为2）的ARMA模型的预测结果。结果表明，基线模型虽然模拟了信号的主要波动特征，但遗失了绝大多数细节部分的波动特征，这是因为基线模型只考虑了一种ARMA模型的拟合过程，只能模拟出一种序列波动特征，而集卡周转时间受到许多因素的影响，有些因素可能会造成其在短期内剧烈变化但振幅不太大的波动，而有些因素则可能造成其变化较为平缓但在整体上振幅较大的波动。如果以上两种因素都存在于原信号中而该信号又被单一的ARMA模型所拟合，那么前者往往会被后者所屏蔽，使得许多细节无法被模型还原。而通过小波分解分离原信号在不同时频层次上的特征来构建多个ARMA模型，可以使预测精度大幅提升。

4 结论与展望

通过对集装箱码头闸口数据进行深入挖掘，提出一种基于小波分解的集卡周转时间预测方法，并利用实际数据进行了有效性验证。研究结果表明，该方法可以较为准确地预测短期内不同任务类型的集卡港内周转时间，其鲁棒性也得到了证明。集卡周转时间预测信息的发布能够为物流企业或集卡公司合理安排运输计划提供切实有效的引导，继而提升整个物流系统的作业效率。未来的主要研究方向是通过基于多源数据融合分析的因果推断方法，揭示影响集卡周转时间的具体关键因素，并从港口管理者和物流企业经营者两个方面进行综合考虑，形成更加全面的集卡调度方案和港口作业策略，如集卡预约方案设计等。

参考文献：

[1]CABALLINI C， GRACIA M D， MAR-ORTIZ J， et al. A combined data mining-optimization approach to manage trucks operations in container terminals with the use of a TAS： application to an Italian and a Mexican port[J]. Transportation Research Part E， 2020， 142： 102054. DOI： 10.1016/j.tre.2020.102054.

[2]LI Le， NEGENBORN R R， DE SCHUTTER B. Intermodal freight transport planning： a receding horizon control approach[J]. Transportation Research Part C， 2015， 60： 77-95. DOI： 10.1016/j.trc.2015.08.002.

[3]SCHEPLER X， BALEV S， MICHEL S， et al. Global planning in a multi-terminal and multi-modal maritime container port[J]. Transportation Research Part E， 2016， 100： 38-62. DOI： 10.13140/RG.2.1.1216.9846.

[4]ZHOU Chenhao， LI Haobin， LEE B K， et al. A simulation-based vessel-truck coordination strategy for lighterage terminals[J]. Transportation Research Part C， 2018， 95： 149-164. DOI： 10.1016/j.trc.2018.07.015.

[5]FAN Houming， REN Xiaoxue， GUO Zhenfeng， et al. Truck scheduling problem considering carbon emissions under truck appointment system[J]. Sustainability， 2019， 11（22）： 6256. DOI： 10.3390/su11226256.

[6]LI Na， CHEN Gang， NG M， et al. Optimized appointment scheduling for export container deliveries at marine terminals[J]. Maritime Policy & Management， 2020， 47（4）： 456-478. DOI： 10.1080/03088839.2019.1693063.

[7]LI Na， CHEN Gang， GOVINDAN K， et al. Disruption management for truck appointment system at a container terminal： a green initiative[J]. Transportation Research Part D， 2018， 61： 261-273. DOI： 10.1016/j.trd.2015.12.014.

[8]PINEDA C， SCHWARZ D， GODY E. Comparison of passengers behavior and aggregate demand levels on a subway system using origin-destination surveys and smartcard data[J]. Research in Transportation Economics， 2016， 59： 258-267. DOI： 10.1016/j.retrec.2016.07.026.

[9]FU Xin， LUO Wei， XU Chengyao， et al. Short-term traffic speed prediction method for urban road sections based on wavelet transform and gated recurrent unit[J]. Mathematical Problems in Engineering， 2020： 1-13. DOI： 10.1155/2020/3697625.

（編辑 赵勉）