小学数学思想的有效培养策略
段慧越
小学是学生学习数学的关键阶段,也是训练良好数学思维和积累数学核心素养的关键时期。学好数学不仅仅是掌握数学基本技能,包括加减乘除的四则运算和识别各种几何图形,更加重要的养成良好的数学思想,这也是学生受益终身的核心素养。虽然小学数学知识很初等、很简单,但是小学数学里面却蕴涵了一些深刻的数学思想。包括数形结合、转换思想、极限思想和归纳思想……主要教学目标都是帮助小学生们深入理解数和图形的对应关系、数和数之间的变化关系等。良好的数学思想能激发他们积极投身探索数学难题的热情,更对学生正确解题和学习更加复杂的数学具有重要意义。
一、在小学教学中渗透转化思想,实现学习的有效转化
转化思想包括将算术公式转化为好记忆的口诀,还有几何图形在边长面积方面的转化。通过转化降低解题难度,得到相应的结果。
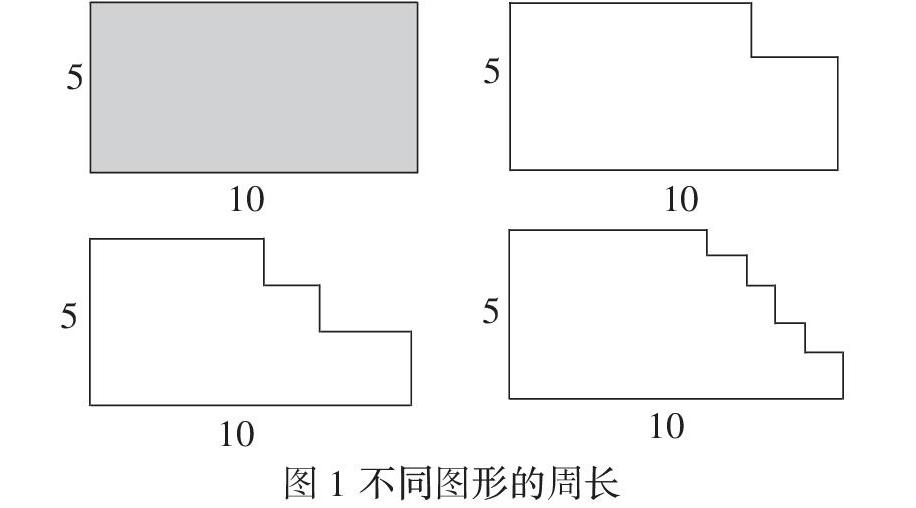
比如:求下面图形的周长?(单位:m)
图1 不同图形的周长
分析:在解决这类问题时,如果不把求第二、第三、第四个图形的周长这些问题转化,仅仅是根据周长的定义——图形边线一周的长度就是图形的周长,把图形每一条边相加,那是很难计算出来的,因为构成图形的一些的长度并不知道。这时我们可以引导学生通过把线段平移,把第二、第三、第四个图形平移成第一个图形的形状,从而把问题转化为只需要求第一个图形的周长即可。这里把一个复杂的问题转化为简单问题,实现学习的有效转化,提高学生解决问题的能力。
解答:四个图形的周长都为: 。
二、在小学教学中渗透数形结合思想,实现抽象问题具体化
数形结合也是小学数学重要思想之一,它将形象直观的图形和规律性强、适合计算的数字灵活转换,让学生更容易得到结果,降低解题难度。
〇有3个, 的个数是〇的2倍, 有多少个?
分析:北师大版二年级上册初次出现倍数应用题,在以后的学习中将会频繁出现。求一个数的几倍用乘法容易与求一个数是另一个数的几倍用除法相混淆。这时,我们可以通过数形结合的方法,帮助学生初步建立起倍数的意义,即:求一个数的几倍是多少就是求几个这样的数的和是多少。要求 的个数就是要求〇个数的2倍,即是两个3的和。在这个基础上,再运用形的思想-画线段图的方法,数形结合。数形结合让小学生从具体的图形转换到抽象的数字,为后续的学习奠定了良好的基础。
解答: (个),答: 有6个。
三、在小学教学中渗透函数思想,更多体验变化中的数量关系
小学阶段经常出现二个相关联的事物,一个的数量随着另外一个变化,这种变化关系从本质上讲就是函数,函数思想的本质在于建立和研究变量之间的对应关系。
乘法口诀是中华文明的瑰宝,也是中华民族智慧的结晶。九九乘法表里蕴涵着许多数学思想,其中函数思想就是其中一个。在记忆九九乘法表时,教师可以让学生理解乘法表,明白上一句口诀与下一句口诀的关系。比如七七四十九,下一句是七八五十六,学生很容易发现49和56之间只相差了一个7, 。再下一句七九六十三。56和63之间也是相差了一个7, 。这样我们就可以运用加法来帮助记忆乘法。这里 实质上包含了变量和函数的思想:7变成8再变成9, 对应的49就变成56再变成63。这里不是把7、8和9看成独立的数, 而是看成一个变量不同的取值。把规律呈现给学生,不仅仅能为背诵九九乘法表增添一丝乐趣,同时能教给学生有趣的思考方式以及学习方法,培养了学生良好的数学思维。
四、在小学教学中渗透极限思想和归纳思想,培养数感
和前面所讲到的转换思想、数形结合相比,极限思想和归纳思想对小学生的数学素养要求更高。极限思想和归纳思想属于高阶数学思想,小学生应用起来比较困难,更多的是探索和接触,建立起一定的概念。
在教学中,让学生通过对算式值的估测,感悟出算式值的范围,培养学生的数感,发展学生的数学思想方法。
(一)在小学教学中渗透极限思想
在对“奇数”和“偶数”的概念教学时,教师可以让学生举更大的数,无论举的数有多大,这个数要么是奇数要么是偶数。进而引导学生体会到奇数、偶数是数不完的,奇数、偶数的个数有无限多个,让学生初步体会到“无限”思想。在推导圆的面积计算过程中,先把圆切成8块,再依次把圆平均分成16、32分,拼成的图形接近长方形的形状;最后运用多媒体帮助学生进一步感知当分的份数越来越多,一直分下去,拼成的图形就会越来越像长方形。这个一直分的过程,實际上就是在渗透极限的思想,通过形象思维引导学生体会极限思想,感受“化曲为直”的神奇。
(二)在小学教学中渗透归纳思想
在研究一般性问题之前,先研究几个简单的、个别的、特殊的情况,从而归纳出一般的规律和性质,这种从特殊到一般的思维方式称为归纳思想。
一道带有规律性的计算题如下:
这里用到的就是不完全归纳。
小学数学教学贯彻数学思想培养,有助于小学生们更好地理解数学和解答题目,感受数学的精髓。教师要帮助他们学习用数学的眼光看待问题, 初步理解数学思维,发展数学素养。

