随机振动下柔性电路板的振动特性分析

代承霖

(中国飞机强度研究所，陕西 西安 710065)

1 引 言

近年来，随着科学技术的快速发展，以柔性电路板为代表的柔性结构件逐渐在芯片工业、生物医疗保健以及相关交互互联领域崭露头角并取得了长足的发展[1-13]。柔性结构的高弹性、高韧性结构特征，使其在监测生物软组织、曲面结构件等特殊环境方面有着独有的优势，并助推了这一行业的兴起。柔性结构的优势有效弥补了传统监测传感器刚性过大的缺陷。传统监测传感器由于硬质的基材料特征，愈发不能适应目前的复杂使用环境[14-17]。因此，结合柔性结构与电路学能有效提高传感器结构弹性，使之克服使用环境的严苛限制。尤其是近年来逐步发展起来的微纳米加工技术和柔性材料制备技术，给柔性电路板的制备带来了希望[18-27]。

柔性电路板(Flexible Printed Circuit，简称FPC)采用的是柔性绝缘基材。随着柔性印制电路板应用越来越广泛，应用柔性电路板的电子产品对结构安全性提出了越来越高的要求，特别是针对动力学环境。然而，目前针对柔性电路板的动力学研究并不充分，且研究角度多从外环境激励着眼，缺乏对结构本身动特性的分析。因此，为进一步了解柔性电路板的动力学特征，明确柔性电路板的设计准则，有必要从柔性结构本身动力学特征研究出发，分析柔性电路板结构在实际高动态特征环境下的力学表征。

模态振型作为结构的典型动力学特征，能说明结构在具体环境下的具体振动情况，故本文以柔性电路板的振型特征计算分析为切入点，在了解柔性电路板结构及随机振动等相关技术的基础上，简要介绍模态分析理论，说明实模态分析法和复模态分析法后，应用COMSOL Multiphysics有限元仿真技术对附着有电子元器件的柔性电路板进行仿真计算，总结该结构的模态振型情况，并根据不同随机振动PSD谱输入，计算绘制相对应的应力应变云图，分析该柔性电路板的随机振动特性。

2 振动分析理论

模态振型是结构的一种固有动力学特征，该特征能说明结构在特定频域下的具体振动情况，直接影响结构的动力学性能。结构自发生激励或受撞击、冲击等外界激励，都将激起结构振动，而这种振动是由各个固有频率下的模态振型按照不同系数叠加而成的。当激励频率与结构的某一阶固有频率相近或相同时，整个结构将呈现出这一阶振型所对应的特定振动形式，且该状况下的振动水平将得到显著加强。

结构在外激励下的广义振动微分方程可表示为：

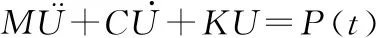
(1)

其中，M、C和K分别为结构的质量矩阵、阻尼矩阵和刚度矩阵，且均为正定对称矩阵，U是结构的位移响应，P(t)是激励载荷。

若结构无阻尼或在阻尼形式为比例阻尼等经典阻尼时，所得模态矢量均为实矢量。振动微分方程可写为：

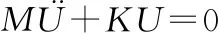
(2)

结构的模态矢量矩阵Φ和固有频率矩阵p呈正交关系：

ΦTMΦ=I

(3)

(4)

其中，I为单位矩阵，p为对角矩阵。

当存在经典阻尼时，存在：

(5)

结构的位移矢量U与模态响应矢量Y存在变换关系：

U=ΦY

(6)

将式(6)代入式(1)，可得由模态响应矢量表示的振动微分方程：

(7)

将式(7)左乘ΦT，根据式(3)-式(5)，可得：

(8)

其中，PΦ和CΦ为：

PΦ=ΦTP

(9)

CΦ=ΦTCΦ

(10)

在式(8)中任提取一个方程：

(11)

称为模态坐标系下的动力学方程，可采用和单自由度系统一样的求解方法，由此可得式(11)的脉冲响应函数：

(12)

将式(12)组合起来，即构成模态脉冲响应函数矩阵：

(13)

hi(t)对应的频域响应函数为：

(14)

将式(14)组合起来，即构成模态频域响应函数矩阵：

(15)

得模态响应矢量各分量为：

(16)

3 柔性电路板有限元分析

本文基于有限元方法及相应的有限元分析软件分析柔性电路板的振动特性，并评价所建立的柔性电路板的动力学性能。

COMSOL Multiphysics是一款以有限元解法为基础，见长于多场耦合分析计算，通过求解偏微分方程实现数值仿真与模拟的商业软件。本文采用COMSOL自带绘图工具绘制模型，基板长0.3m、宽0.2m、厚1.5mm。基板上附着有铝基散热装置、硅基及亚克力塑料等电子元器件，模型三维图如图1所示。

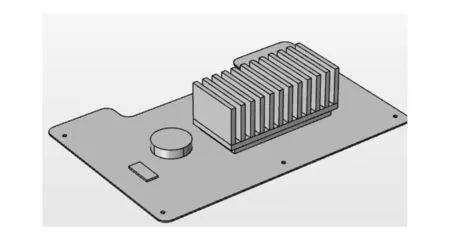
图1 柔性电路板结构

结构力学模块所需材料属性主要为杨氏模量、密度、泊松比。本文所构建的模型主要由基板及附属电子元器件组成，基板材质为聚酰亚胺，附属电子元器件材质分别为硅、金属铝、亚克力塑料及电容器材料。材料性质如表1所示。

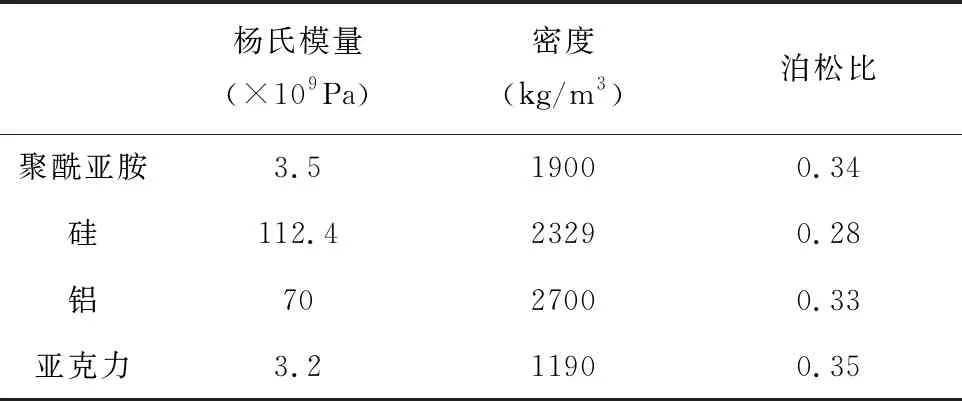
表1 材料特性

该柔性结构采用自由剖分六面体网格划分模型，为在聚酰亚胺基板区域求得更精确的计算结果，该区域的网格较为精密，其余网格较为粗糙。该电路板处于边界固定约束状态，对其做两种随机振动工况下的计算并分析其动力学特性，图2为输入的随机振动PSD谱。

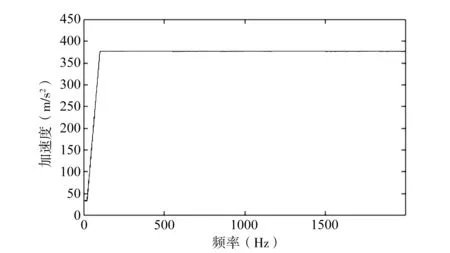
图2 随机振动PSD谱

本文计算了该柔性结构的前12阶模态振型情况，在这里取前4阶模态振型进行典型分析。图3-图6为该柔性电路板的前4阶模态振型图，该模型的前4阶全局固有频率分别为57Hz，97Hz，106Hz和141Hz。从振型图可以看到，振动主要集中于聚酰亚胺基板区域上，故该附着各类电子元器件的柔性电路板可看作类平板结构。

图3 第1阶模态振型图

图4 第2阶模态振型图

图5 第3阶模态振型图

图6 第4阶模态振型图

本文对该柔性电路板进行时域分析，计算50ms内的时域相应情况。图7为电路板全局应力-时间曲线，图8为电路板全局应变-时间曲线。

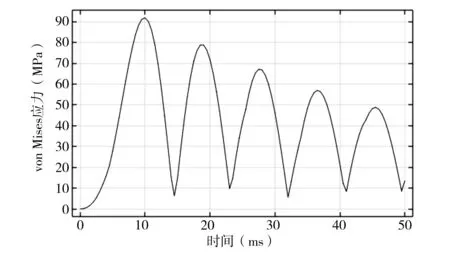
图7 电路板全局应力-时间曲线

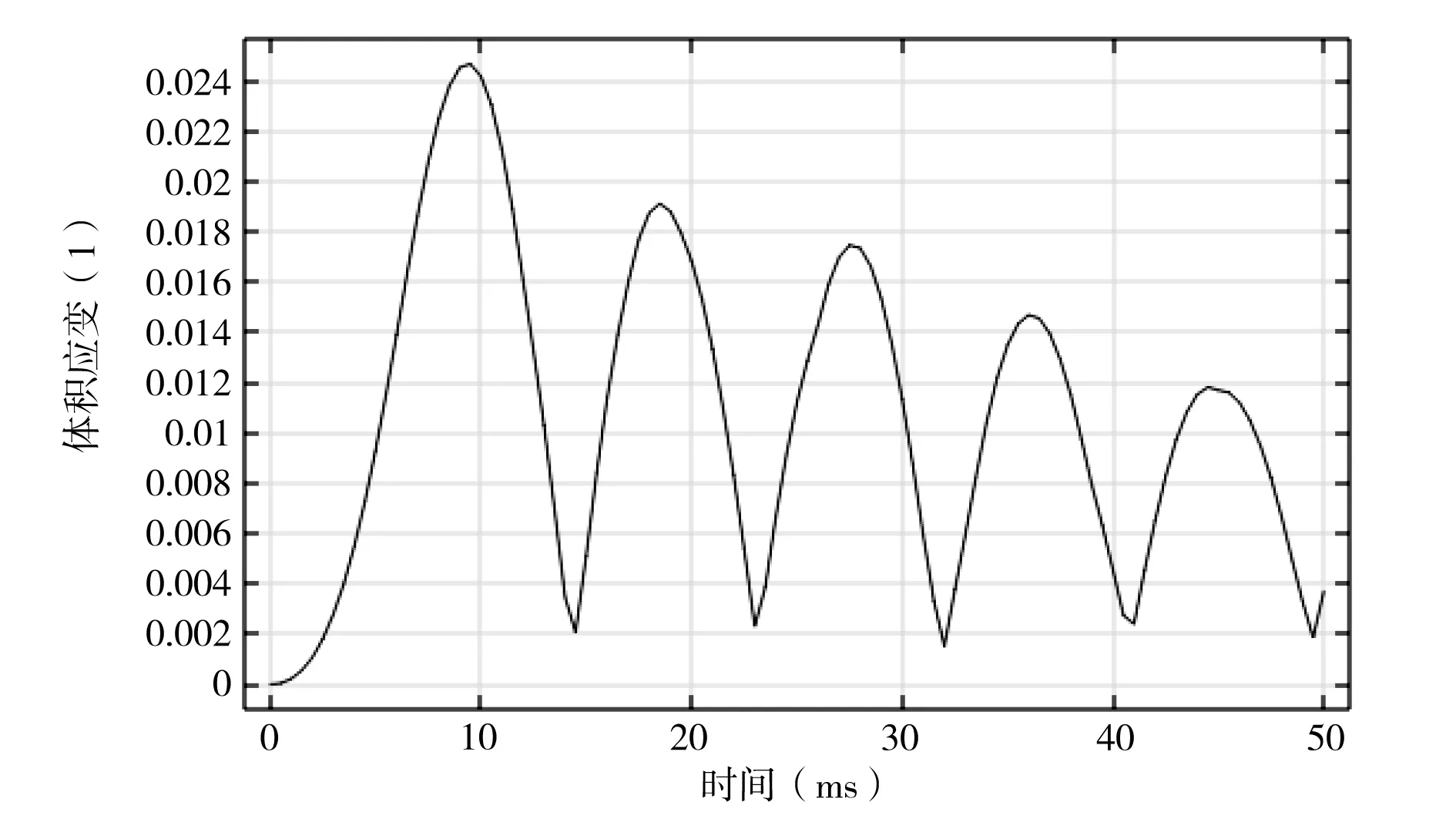
图8 电路板全局应变-时间曲线

由图可知，响应峰值出现在9ms、18ms、27ms、36ms和45ms。为了进一步明确该柔性电路板的响应分布特征，本文整理了该结构在9ms、18ms、27ms、36ms和45ms时的应力、应变云图。图9-图13分别为该结构在9ms、18ms、27ms、36ms和45ms时的应力分布图，图14-图18分别为相对应的应变云图。由图可知，该柔性电路板在9ms、18ms、27ms、36ms和45ms时，应力、应变主要集中于固定约束处、等效质量较大处。

图9 9ms时的应力云图

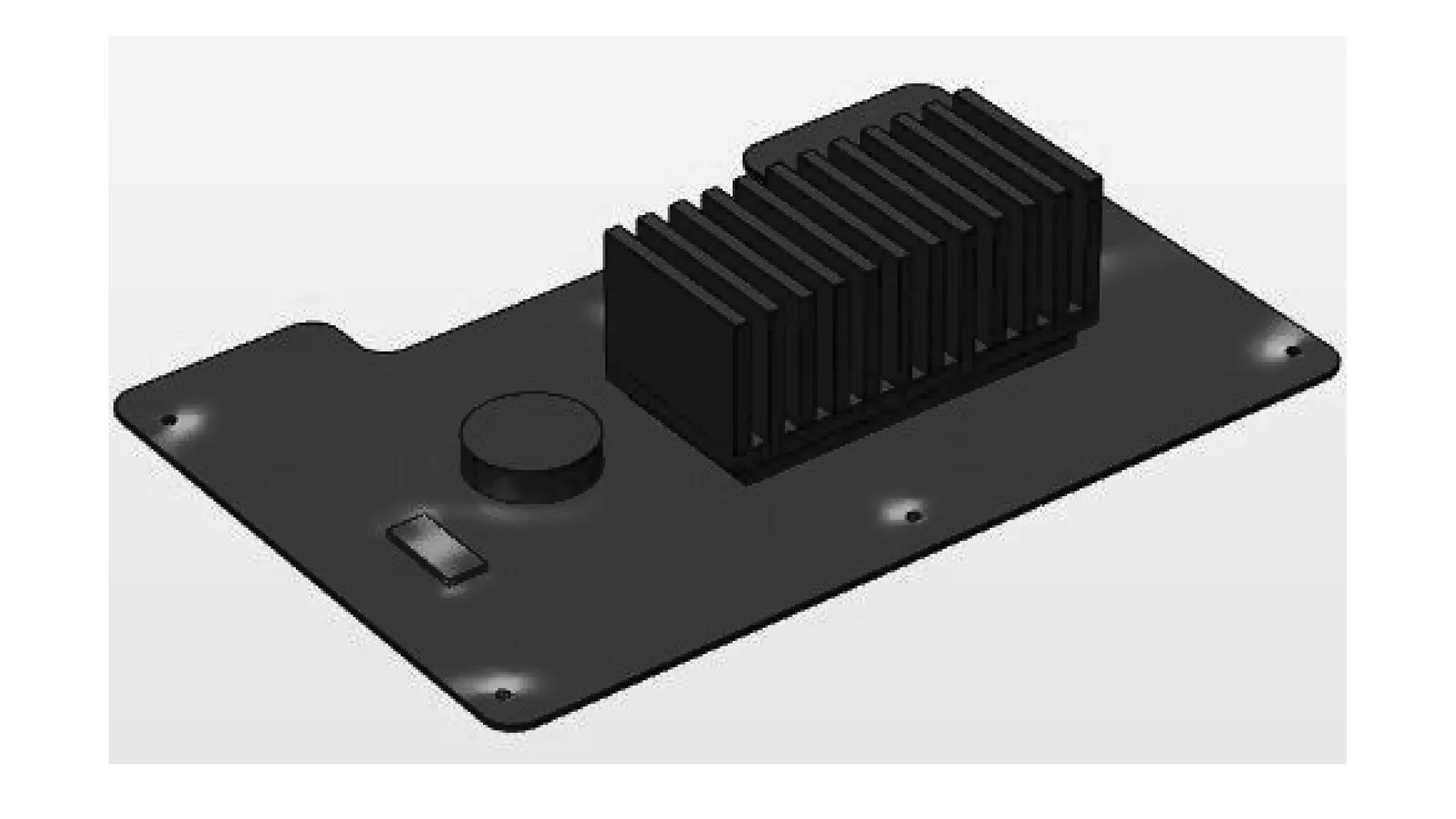
图10 18ms时的应力云图

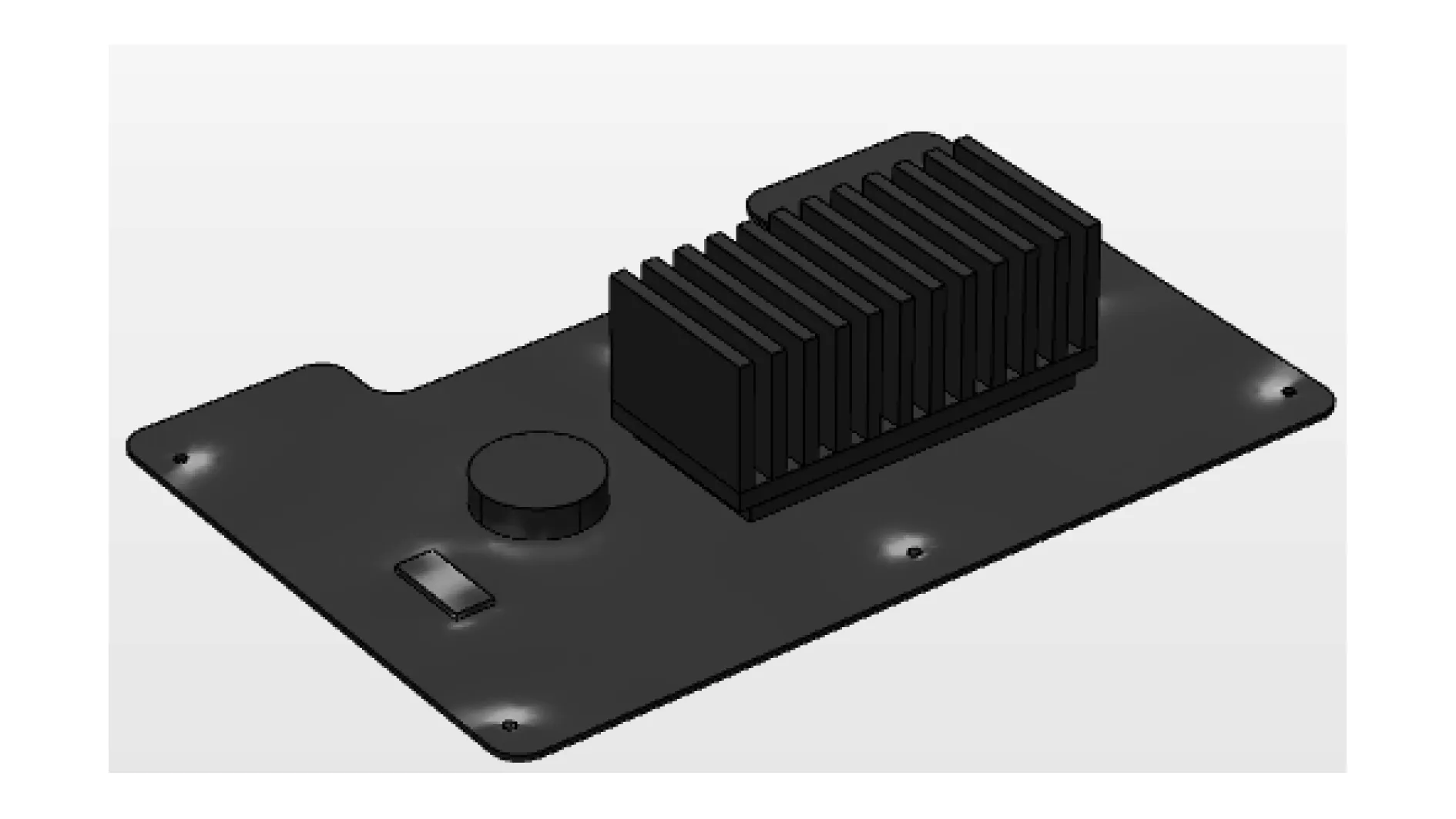
图11 27ms时的应力云图

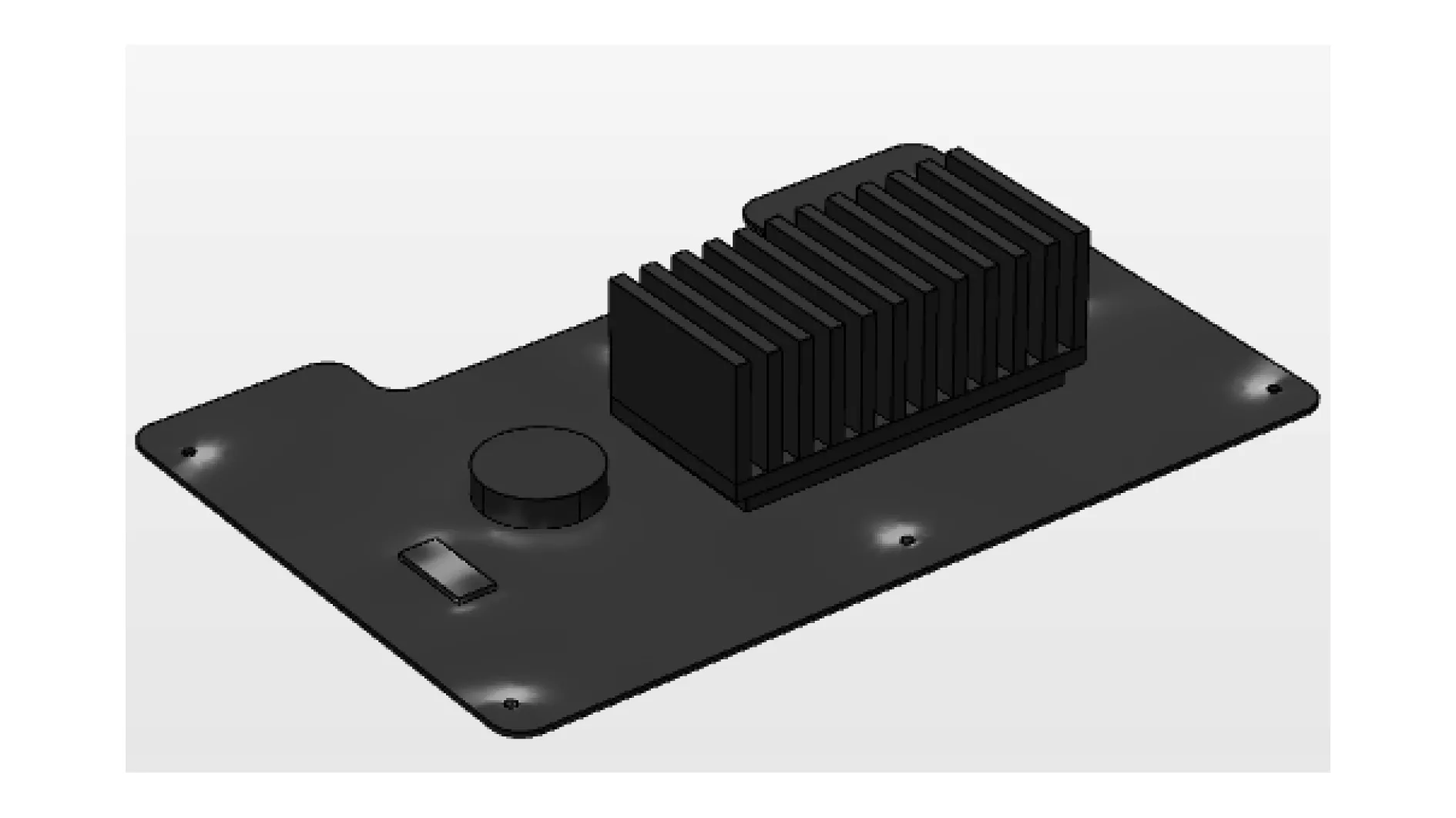
图12 36ms时的应力云图

图13 45ms时的应力云图

图14 9ms时的应变云图

图15 18ms时的应变云图

图16 27ms 时的应变云图

图17 36ms时的应变云图

图18 45ms时的应变云图

由此可知，在长期动载荷激励下，该柔性电路板由于在固定约束处、等效质量较大处存在大应力、大应变，容易出现分层破坏现象，影响结构的使用安全。为避免应力集中造成的电子元器件损伤失效，本文认为可通过电子元器件的合理布局避免由应力过大引起的损伤性现象。结合模态分析结果，可得出散热片附近区域应力值较小，该区域的振动局域化现象不突出的结论，尽可能将所附着的电子元器件集中排布于散热片附近，将有较好的保护效果。

4 总 结

本文以附着电子元器件的柔性电路板为目标结构，就该柔性电路板建立了振动理论模型，设计了一种附着电子元器件的柔性电路板并通过仿真计算对其动力学特性进行分析。结果表明，在长期动载荷激励下，该柔性电路板在固定约束处、等效质量较大处存在大应力、大应变。为避免应力集中造成的电子元器件损伤失效，可通过电子元器件的合理布局避免由应力过大引起的损伤性现象。