谐振子势阱中双费米原子光钟的碰撞频移*
陈泽锐 刘光存 俞振华
(中山大学物理与天文学院,广东省量子精密测量与传感重点实验室,珠海 519082)
原子钟提供了时间的标准,但原子间的相互作用往往限制原子钟的精度.本文理论研究了谐振子势阱中双费米原子光钟由于原子间的短程相互作用而在拉比频谱中引起的碰撞频移.考虑到原子光钟中短程相互作用一般较弱,并且晶格光的参数在Lamb-Dicke 区间中,本文近似费米原子的外态不发生改变,进而推导出原子内态在拉比探测光驱动下满足的运动方程.微扰求解运动方程,得到一阶解的解析表达式,从而得到了拉比频谱的碰撞频移依赖于拉比探测光参数与在原子特定外态中相互作用的表达式.最后,利用谐振子势阱中格林函数的解析表达式,得到了有限温下碰撞频移与原子间相互作用的关系.研究结果表明,实验中可以通过精密测量原子光钟的频移获得原子间相互作用的信息.
1 引 言
作为定义时间的科学标准,原子钟从上个世纪开始就是一个众多学者致力研究的活跃领域[1,2].而近期迅速发展的光频原子钟预示着新一代的时间标准.原子钟性能的每一步提升都难能可贵,人们通过大量的理论研究和实验探索,逐渐实现了将抑制原子钟精度的各种效应所引发的时钟频移限制在相对更低的量级下,诸如多普勒效应、光晶格频移、光子反冲等.长期以来,原子间短程相互作用导致的碰撞频移在各个阶段往往是抑制原子钟性能的重要因素.所以,对原子光钟碰撞频移的研究,不仅对于更高精度原子钟的研制具有重要意义,而且能够加深我们对原子相互作用的认识[3−9].
从原子相干性对Ramsey 条纹的影响[10],到费米原子气体中冷碰撞频移免疫论断的推翻[11,12],及玻色原子气体中碰撞频移令人困惑的 2 − 因子的问题[13−17],再到实验上测量Yb 晶格光钟的冷碰撞频移获得p 波相互作用的贡献[18,19],人们关于原子光钟碰撞频移的认知越来越丰富.而最近实现的三维光晶格中的费米原子气体可以达到晶格格点上的单位填充[20,21],使得完全避免由原子间短程相互作用引起的碰撞频移成为可能.
另一方面,对原子光钟碰撞频移的精密测量可以提供原子间相互作用的宝贵信息,本研究也明显地展示了这一点.本文理论研究了谐振子势阱中双费米原子光钟由于原子间的短程相互作用而在拉比频谱中引起的碰撞频移,从而得到了拉比频谱的碰撞频移依赖于拉比探测光参数与在原子特定外态中相互作用的表达式.并且,利用谐振子势阱中格林函数的解析表达式,得到了有限温下碰撞频移与原子间相互作用的关系.这些结果都表明精密测量原子光钟的频移可以成为探测原子间相互作用势能性质的重要实验手段.
2 理论模型
本文研究的物理过程是谐振子势阱中费米原子光钟在拉比脉冲作用下的光钟跃迁.为揭示原子间短程相互作用对光钟跃迁的影响,考虑在谐振子势阱中的双费米原子系统.对于该问题,系统的哈密顿量如下:
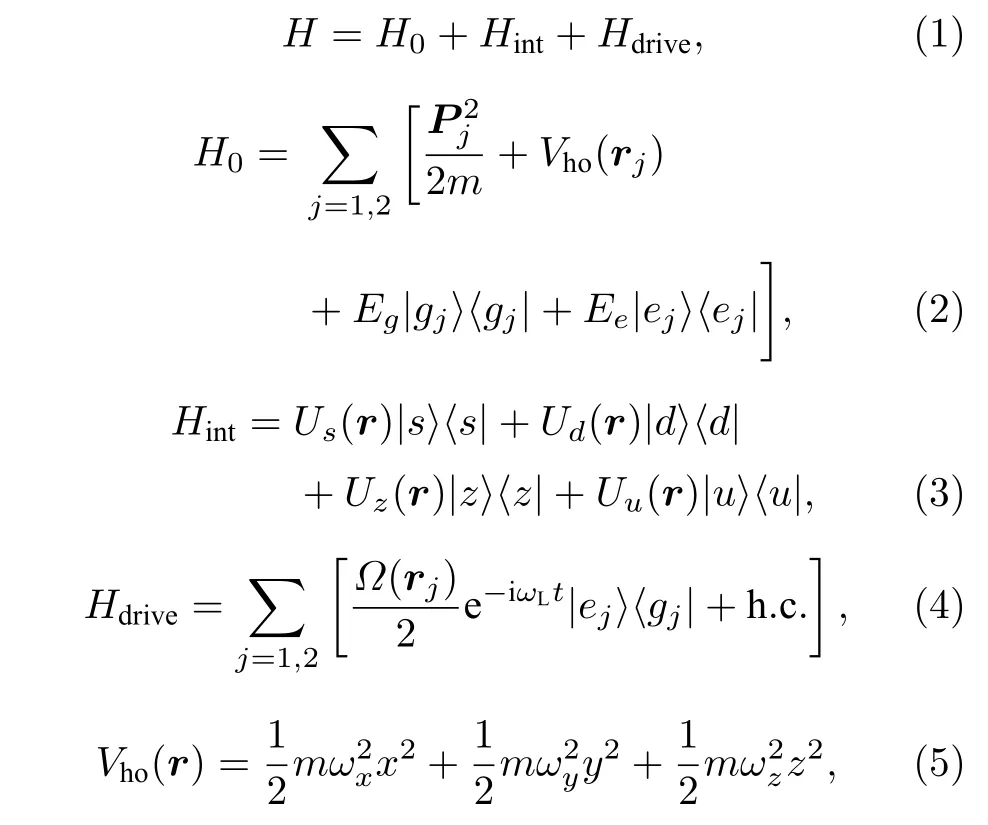
式中,下标j代表第j个原子,m为原子质量,|g〉和|e〉为原子内态的两个钟态,Eg和Ee表示对应能级.原子间的相互作用Hint被分解到两个原子内态的单重态和三重态子空间中:
假设各子空间中的势场Uα(r)(α=d,z,u)为中心势场.本文考虑的谐振子势阱为一般情况,即3 个方向的束缚频率ωx,ωy,ωz各不相同.驱动哈密顿量Hdrive来源于拉比探测光与原子电偶极矩的耦合.由于选择激光频率ωL接近原子的光钟跃迁频率ω0≡Ee −Eg,即失谐量δ≡ωL−ω0的模量远小于ω0,我们已采用了旋转波近似.原则上,拉比频率Ω(r) 依赖于原子位置r.
3 运动方程
一般情况下,原子间的相互作用能比谐振子势阱的束缚频率小很多.假设先不考虑拉比探测光的驱动,那么对于两个费米原子而言,如果内态处在三重态,则外态波函数应为相应地,如果内态处在单重态,那么外态波函数应为这里的ϕa(r) 是谐振子势阱中单原子的本征波函数,具有本征能量ϵa.而当加上拉比探测光时,为防止在拉比探测光作用下原子光钟跃迁的同时发生反冲,谐振子势阱的束缚频率往往被调得很大,使系统处在Lamb-Dicke 区域,即原子的外态不会发生改变.

显然,相互作用能的大小依赖于两个原子空间波函数的交叠情况.由于原子间的相互作用能很小,连同初始值d(t=0)=1,z(t=0)=u(t=0)=0 解析求解(13)式到Uα,ab的一阶(详细结果见附录A).
4 光钟频移
光钟拉比频谱的工作程序是将原子制备到|g〉初态,然后拉比探测光施加一个时长为tπ的π脉冲,即Ωtπ=π,接着再测量激发到|e〉态的原子概率Pe.对于本文研究的双费米原子的问题

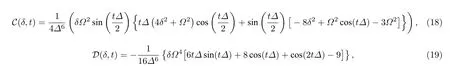
拉比频谱确定频移的方法是找到两个拉比探测光的失谐量δr(<0)和δb(>0) ,使得在 π 脉冲后
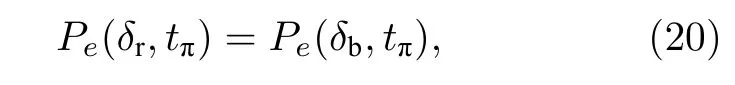
频移δs就被定义为

要从(16)式和(19)式推导出δs的解析表达式,我们在蓝失谐侧选取一个较小的参考失谐量δR(>0) .根据(20)式的定义,有
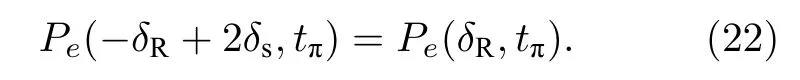
仍然利用原子间的相互作用能比较小的特点,这样频移δs也会比较小.泰勒展开(22)式左边到δs的一阶,得到
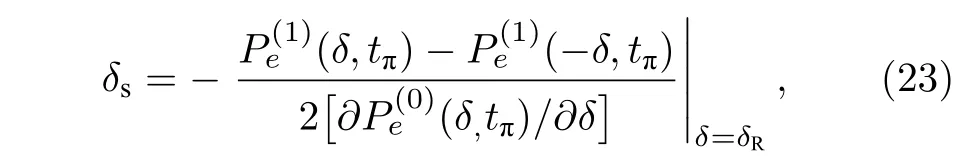
将(16)式和(19)式代入(23)式,计算得到
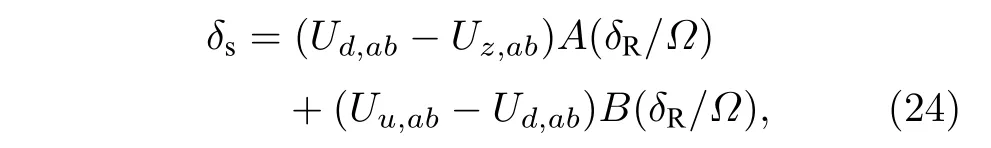
其中
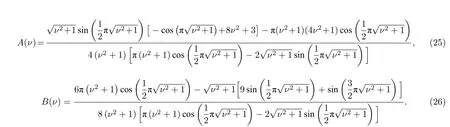
(24)式反映了 π 脉冲激光参数ν=δR/Ω和原子间相互作用能Uα,ab(α=d,z,u)对频移δs的贡献.δs只依赖于Uα,ab(α=d,z,u)的差值,因为如果Uα,ab(α=d,z,u)都相同的话,(13)式中相互作用能只是把三重态的能量整体频移了一下,不可能影响光钟频移.图1 显示在实验关心的区间δR/Ω~1/2,A和B的模量都是1的量级.从另一个角度看,(24)式表明通过测量δs在两个不同δR时的值,就可以反推出Uα,ab(α=d,z,u)之间的差值.如要获得单独Uα,ab(α=d,z,u)的值,实验则需选取特定的量子态使得至少一个Uα,ab(α=d,z,u)的值为 0 .
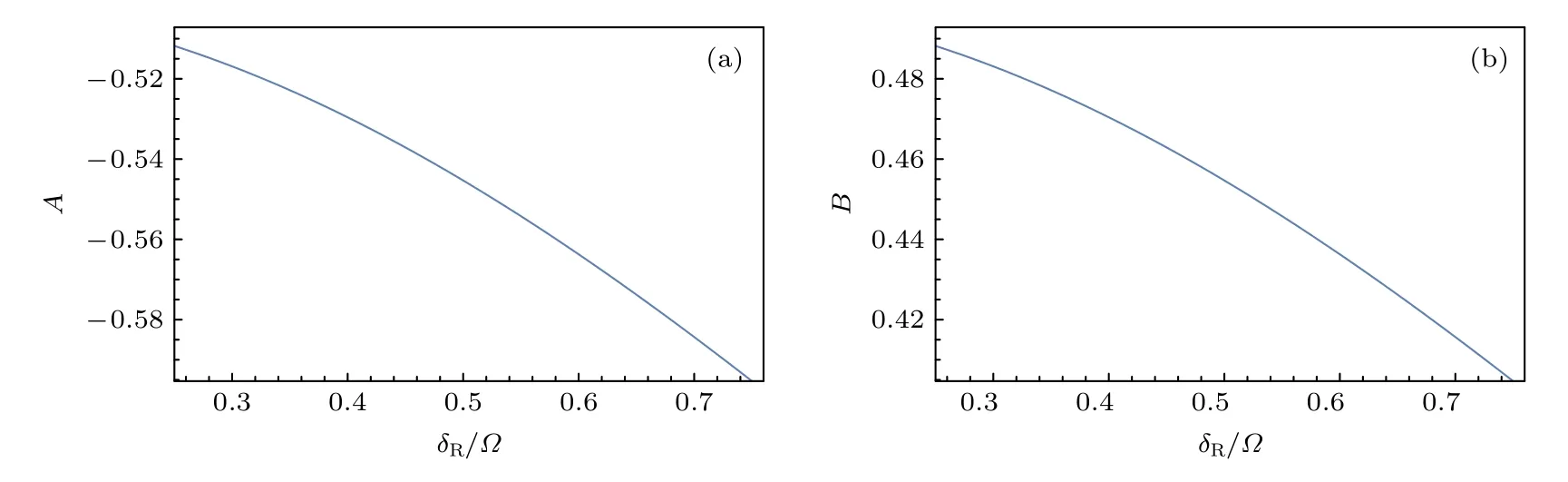
图1 光钟频移系数(a) A(δR/Ω) 与(b)B(δR/Ω)Fig.1.Coefficient(a) A(δR/Ω) and(b) B(δR/Ω) for clock shift.
在此值得强调的是,以上求解钟频移的方法要求拉比谱的线形是光滑的.这一前提对于本文考虑的弱相互作用情形是满足的,但当相互作用足够强时,拉比谱会出现边带峰[18],这种情况下以上求解钟频移的方法就不再适用了.
5 有限温平均


其中,归一化系数Z为


6 结 论
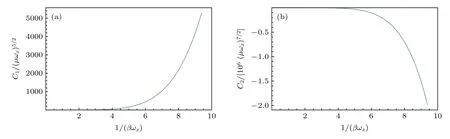
图2 系数 Cℓ 随温度的变化 (a) C1;(b) C2Fig.2.Coefficient Cℓ versus temperature:(a) C1;(b) C2.
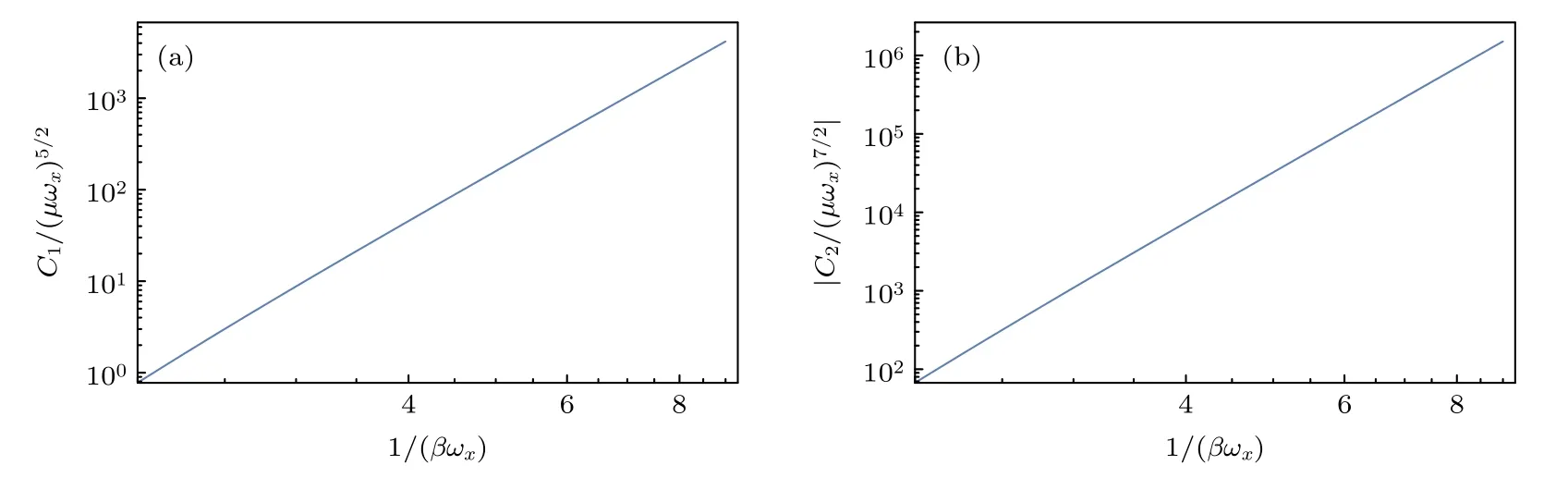
图3 当温度较高时,系数 Cℓ 随温度的变化,这里横轴和纵轴都取对数 (a)线性拟合表达式为 y =5.54203x-3.83918 ;(b)线性拟合表达式为y=6.5296x-0.119146Fig.3.Coefficient Cℓ versus temperature for higher temperature.The horizontal coordinate and the vertical coordinate are logarithmic here:(a) Linear fitting function is y =5.54203x-3.83918 ;(b) linear fitting function is y =6.5296x-0.119146 .
本文研究了双费米原子拉比激发过程中短程相互作用引起的碰撞频移.计算结果给出了碰撞频移依赖于原子相互作用的关系.相较 以前碰撞频移的理论研究只考虑了s 波及p 波,本文提供了各阶贡献的统一表达式.本文的结果意味着通过精密测量碰撞频移可以获得原子间相互作用的重要信息.如果要将本文双费米原子的结果拓展到多费米原子的情况,可以预见的是,在弱相互作用极限下,多原子体系的相互作用效应仍应来源于原子两两之间的碰撞,即相互作用能是所有粒子对的总和,形式为这里fi为费米原子在第i个谐振子本征态上的占据数,gij是占据i和j本征态原子发生碰撞而导致的耦合系数.对多费米原子情况的研究将是我们下一步的课题.
附录A 运动方程(13)的零阶解和一阶解
通过微扰的方法可解得运动方程(13)的零阶解:

附录B (29)式的推导
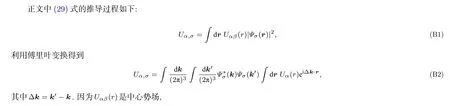

附录C 高阶分波对钟频移的贡献
为了定量化高阶分波对钟频移的贡献随温度的变化,由(36)式计算截断求和到第ℓ阶的值,即(ℓ) .为了完成定量计算,采用方势阱模型势Uα(r)=Uα,0θ(r-r0) .这里势阱力程r0应为范德瓦耳斯半径的量级,取成r0=1 nm.而势阱深度的取值,参考实验论文[18],分别为Ud,0=0,Ut,0=-4.4π Hz 以及Uu,0=-0.44π Hz.当δR/Ω=1/2 时,如图C1 所示,当温度很低时,同时考虑s 波至d 波(s,p,d)时的钟频移(ℓ=2) 同只考虑s 波至p 波时的钟频移(ℓ=1)的差值极小,即d 波分量引起的钟频移接近零.当温度升高时,以上两者差值逐渐增大,表明d 波贡献的钟频移量也在逐渐增大.由本文的解析表达式可推知,更高分波的贡献也有相同的趋势.
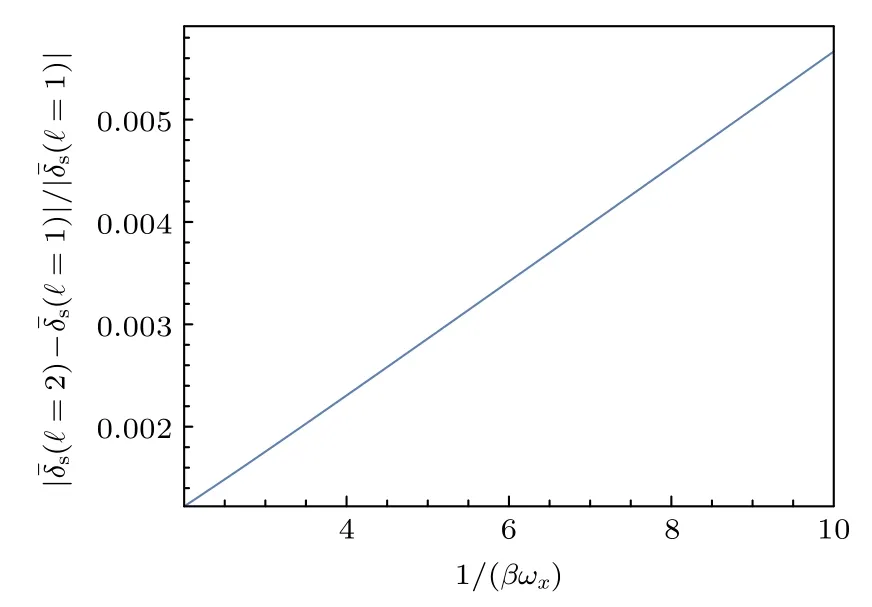
图C1 同时考虑s 波至d 波时的钟频移(ℓ=2) 与只考虑s 波和p 波时的钟频移 (ℓ=1)的相对误差Fig.C1.Relative error of clock shifts between considering s,p,d partial waves((ℓ=2)) and only considering s,p partial waves((ℓ=1)).

