大口径非球面铝反射镜三轴联动加工技术研究

肖建国，姚 同，张万清，刘 尧，罗 宏，李茂忠，黄 攀，康 杰，张若寅

（1.云南北方光学科技有限公司，云南 昆明 650200；2.昆明理工大学 机电工程学院，云南 昆明 650500）

0 引言

金属反射镜广泛应用于空间光学、天文观测、高能激光以及太阳模拟器光学系统等领域。随着大型空间光学遥感技术的快速发展，对光学系统中反射镜分辨率的要求不断提高，导致其焦距、视场角、口径不断增大，对其面形精度和表面质量的要求也越来越高，使得大口径反射镜的加工难度日益增加[1-3]。

针对大口径反射镜加工技术的研究，许多学者提出多种加工方法。Horst 等人[4]通过直接抛光法对超精密加工后的铝反射镜进行抛光，可获得较低的表面粗糙度和更高的面形精度，但加工效率低，对复杂面形光学反射镜加工精度难以保证。姜伟等人[5]研究大口径反射镜化学镀镍-磷合金工艺及质量控制方法，但该方法容易引起镀层变形、起皮、开裂等现象。孟晓辉等人[6]提出应用旋转法实现大口径反射镜零重力面形加工，提出基于重力卸载的高精度旋转检测工艺。孙熠璇等人[7]提出适应于大口径反射镜高精度光学加工的重力卸载优化方法，并通过有限元法对多点主动支撑式重力卸载进行参数优化。马文静等人[8]采用有限元方法对大口径反射镜的夹持力进行优化，以避免由装夹变形引起附加变形，实现反射镜低应力夹持。随着单点金刚石切削技术迅速发展，工件可以获得亚微米级的面形精度和纳米级的表面粗糙度，还可对铜、铝、硅、锗等材料加工出“镜面”级表面质量，因此广泛应用于大口径反射镜加工[2]。

单点金刚石车床加工大口径非球面反射镜时，若工件凹面深度超过车床Z轴导轨行程的一半，基于车床导轨位置配置的关系，加工中刀具工作台就容易与工件发生干涉，若工件口径过大就会受到工作台台面回转容积的限制。在这两种情况下，常规的两轴加工模式不能对大口径非球面反射镜进行加工。此外，合适的装夹方式及夹具是保证反射镜加工精度和加工质量的重要前提条件。目前，常用的大口径反射镜的夹具为筒状夹具，即反射镜通过螺栓连接固定于筒状夹具内进行切削加工，但由于反射镜的口径不断增大，所需夹具尺寸也随之增大，筒状夹具自身重量增加、装夹不牢固，使得工件加工变形增大。

针对单点金刚石车削技术应用于大口径非球面铝反射镜加工过程中遇到的车床导轨行程和工作台台面回转容积受限以及加工质量较低的问题，本文提出适用于大口径非球面反射镜三轴联动加工方法，通过坐标变换原理将常规两轴联动加工坐标转换为三轴加工坐标，并编制数控程序，以解决车床导轨行程和工作台回转容积受限问题；然后为提高大口径铝反射镜加工表面质量，通过三维软件UG 设计专用笼状夹具，结合有限元法，研究夹具参数（支撑杆数量、杆径、上下连接板厚度）对夹具-工件变形的影响，通过极差和方差分析得到最优夹具参数组合，实现低应力夹持。最后，利用三轴联动加工方法对口径为φ682 mm 的非球面铝反射镜进行加工。

1 大口径非球面铝反射镜加工过程

本文对大口径非球面铝反射镜的加工技术进行研究。首先提出单点金刚石车床三轴联动加工方法，以满足大口径、大弦高金属反射镜的加工需求。然后对夹具进行设计并优化，使得夹具在满足装夹条件的前提下，减小整体变形，从而降低由于装夹变形对加工后工件面形精度和表面粗糙度产生的影响。

1.1 非球面方程

本研究对大口径非球面铝反射镜进行单点金刚石切削，工件口径为φ682 mm，非球面参数透镜顶点处曲率c为0.0043，非球面圆锥曲线系数k为－0.8751。反射镜尺寸示意图如图1所示。

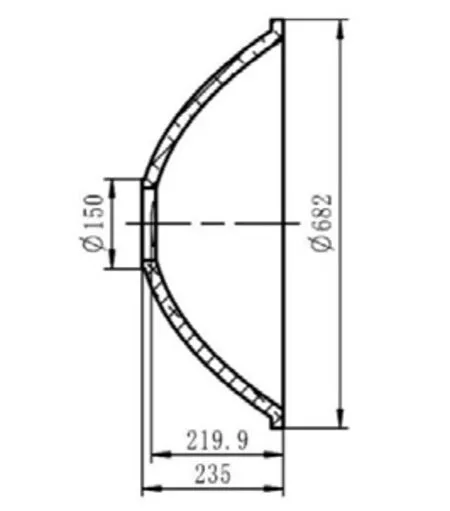
图1 非球面铝反射镜几何参数图Fig.1 Geometric parameter diagram of an aspheric aluminum mirror

反射镜非球面方程为：

式中：c为透镜顶点处曲率；k为非球面圆锥曲线系数；Z轴为非球面旋转轴，即光轴；x为垂直于光轴方向长度；A2ix2i为非球面方程的高次项。

1.2 三轴联动加工方法

单点金刚石加工是目前常用的高精度金属反射镜的加工方法。通常情况下，采用两轴联动加工方式即可实现对铝反射镜凹面的加工。然而，本次研究对象为口径为φ682 mm 的大口径铝反射镜，反射镜凹面深度为219.9 mm，加工使用大型MTC410 型单点金刚石车床，机床结构示意图如图2所示，机床采用X/Z/B三轴配置，其X/Z轴行程均为400 mm，最大加工直径达到φ800 mm，B 轴台面回转容积达到φ550 mm。即便使用此大型单点金刚石车床，受凹面深度、机床导轨行程及B轴台面回转容积等多方面的限制，两轴联动加工方法不能对此大口径、大弦高铝反射镜进行加工。

图2 机床结构示意图Fig.2 Schematic diagram of machine tool structure

因此，为了实现此类非球面反射镜加工，提出大口径、大弦高金属反射镜的三轴联动的加工方法，将金属反射镜面形加工坐标从两轴联动加工的X-Z平面坐标转换为X-Z-B三轴联动加工坐标，其中β为刀具旋转B轴的转动角度。加工示意图如图3所示。该方法通过B轴旋转，可有效解决机床导轨行程及可旋转工作台台面回转容积受限的问题，可实现对超出导轨行程的大口径工件进行加工，同时能够提高加工效率，降低加工成本。该三轴联动的加工方法已申请发明专利[9]。

图3 三轴联动加工示意图Fig.3 Schematic diagram of three axis linkage machining

三轴联动加工方式的关键技术之一是实现X-Z坐标到X-Z-B坐标的变换。本文对坐标变换的原理进行了数学建模，并编制了坐标变换程序。

坐标变换的基本原理如下：首先基于给定的非球面方程相关参数，计算出非球面加工表面的X-Z坐标，即得到图4中A1、A2点坐标(x1,z1)、(x2,z2)。

图4 坐标变换原理Fig.4 Principle of coordinate transformation

由公式(2)可得∠A2A1C2大小：

式中：θ为∠A2A1C2大小。

由三角形性质可知∠A1A1′C1＝∠A2A1C2，即β1＝θ，由公式(3)可得刀尖圆弧中心点A1′的三轴加工坐标[X1,Z1,B1]。

式中：R为刀尖圆弧半径。

由公式(4)可得刀具圆弧中心点在A1′时，刀具工作台与工件上端面间的距离M。当M＞10 mm 时，夹具与刀具旋转台之间不会发生干涉。

式中：L为刀具工作台中心点到刀尖的距离；r为刀具工作台半径；d为工件凹面深度。

由公式(5)可得刀具工作台中心点到工件中心的距离N，当200 mm＜N＜600 mm 时，刀具工作台移动在机床行程内。

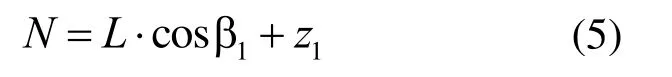
根据上述原理，通过MATLAB 编程软件可得全部刀尖圆弧中心点的三轴坐标以及各点处的M和N值。当M值大于安全距离，且N值处于导轨行程，则坐标变换成立。可根据铝反射镜的最佳拟合半径和刀具尺寸设定坐标系原点及随动变量参数值，将包含三轴加工坐标[X,Z,B]的加工程序输入到单点金刚石车床数控系统进行加工。

1.3 夹具优化

由于工件和夹具尺寸过大，整体自重对加工变形的影响显著，因此需对夹具进行优化。首先，设计出针对大口径反射镜的专用笼状夹具，几何模型如图5所示，夹具由上下连接板和支撑杆组成，工件上下端面与夹具上下板使用螺栓连接，上下板之间由支撑杆连接。笼状夹具与筒状夹具相比，筒壁结构用支撑杆来代替，既能满足对工件的装夹要求，又减少了夹具自身重量，实现夹具轻量化。然后，基于有限元分析和正交试验方法，对笼状夹具进行参数优化，研究夹具支撑杆数量、直径以及上下连接板的厚度对工件变形的影响，通过方差分析和极差分析确定最佳夹具参数组合。

图5 夹具几何模型Fig.5 Geometric model of fixture

采用ANSYS Workbench 软件对夹具-工件几何模型进行前处理。首先，将几何模型进行简化，使用sweep 划分网格，其网格质量为0.77，网格划分后的满足有限元分析要求，夹具-工件有限元模型如图6所示。其次设置材料属性，定义夹具为不锈钢，工件为铝合金，材料参数如表1所示。再定义边界条件，固定主轴圆盘后端面，添加重力加速度，施加转速。最后，输出夹具-工件的应变云图。

图6 夹具-工件有限元模型Fig.6 Finite element model of fixture work piece

表1 材料参数Table 1 Material parameters

2 结果与讨论

2.1 坐标变换

通过非球面方程参数计算出非球面上等步距点的坐标，即得到加工铝反射镜两轴加工坐标[X,Z]，通过上述坐标变换原理，将坐标[X,Z]转换为三轴加工坐标[X,Z,B]，坐标变换结果如表2所示。经计算，M最小值为12.74 mm，N最大值为468.79 mm，均满足机床加工要求。

表2 坐标变换结果Table 2 Coordinate transformation results

2.2 夹具优化结果

本研究采用L9(34)正交表进行夹具优化实验，夹具参数如表3所示。分析结果如表4所示。

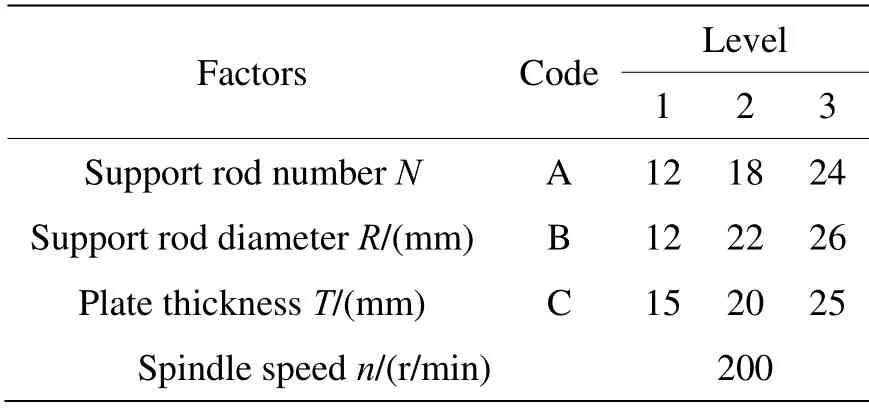
表3 夹具参数Table 3 Fixture parameters

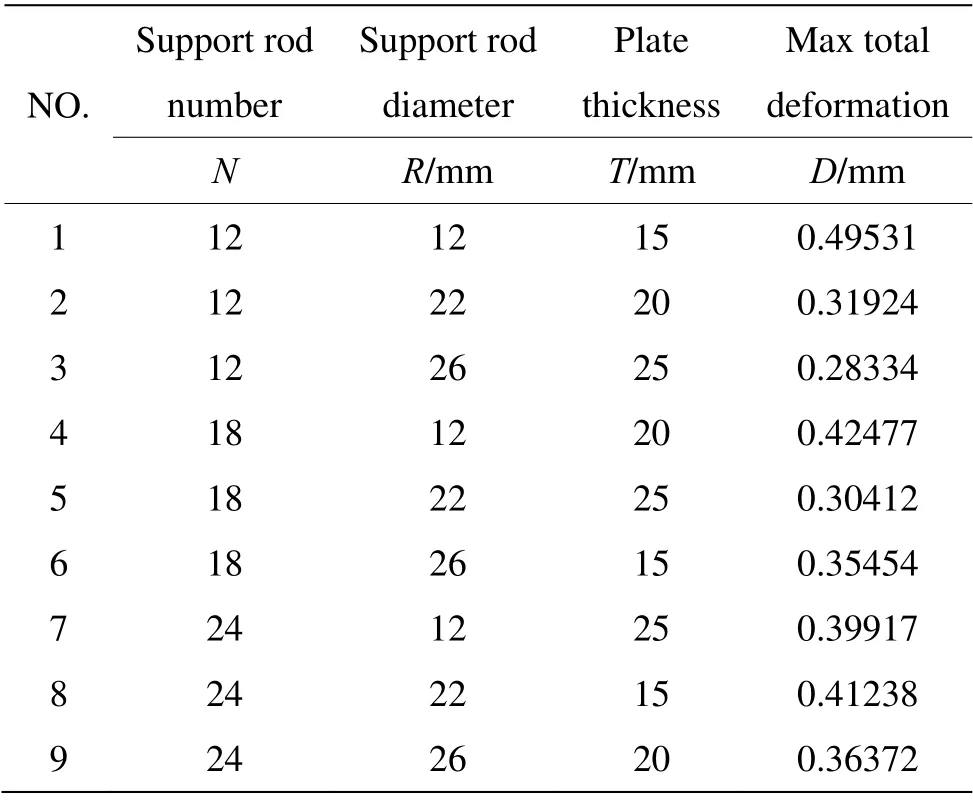
表4 正交实验方案及结果Table 4 Orthogonal experimental scheme and results

最大变形量随支撑杆数量、直径以及上下连接板厚度的变化趋势如图7所示，最大变形量随支撑杆数量的增加先增大后减小。这是由于杆数过少会使工件固定不稳定，整体强度较弱，导致变形量增大；杆数过多将增加整体重量，在加工过程中，自重引起的加工变形将成为主要因素。最大变形量随支撑杆直径和连接板厚度的增加而减小，杆径和壁厚的增加使得夹具强度增加，固定工件更加牢固，使得变形量减小。由图7可知，当杆径由22 mm 增加到26 mm 时，最大变形量仅发生微弱的变化，这是由于杆径的增加在使夹具强度增加的同时增加了自身的重量。因此最终选择支撑杆直径为22 mm。最大变形量随连接板厚度的增加显著减小，因此，应选择板厚为25mm。

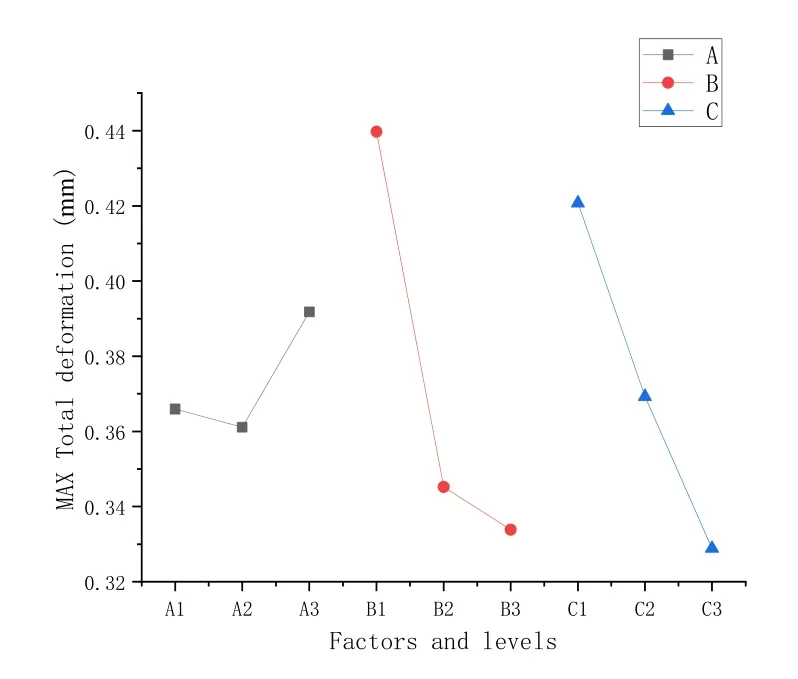
图7 最大变形量随各参数变化趋势Fig.7 The variation trend of maximum deformation with various parameters

对正交实验中最大变形量进行方差分析，探究各夹具参数对最大变形量的影响程度，表5为离差平方和SS、自由度df、均方MS、显著性F以及贡献度（Contribution）的统计量结果。可以看出，影响因素B、C的显著值F较大，并且贡献率达分别到52.6%和31.6%，说明杆径和连接板厚度对装夹变形的影响最大；支撑杆的数量对变形量的影响最小，其贡献率为0.7%。这表明支撑杆的数量在12～24 之间时，其对变形量的影响最小。

表5 表面粗糙度的方差分析Table 5 Analysis of variance of surface roughness

根据方差分析和极差分析最终确定最佳夹具参数组合，即夹具支撑杆的数量为24，支撑杆的直径为22 mm，上下连接板的厚度为25 mm。图8为最佳夹具参数下，夹具-工件的应变云图，夹具和工件的变形最小。

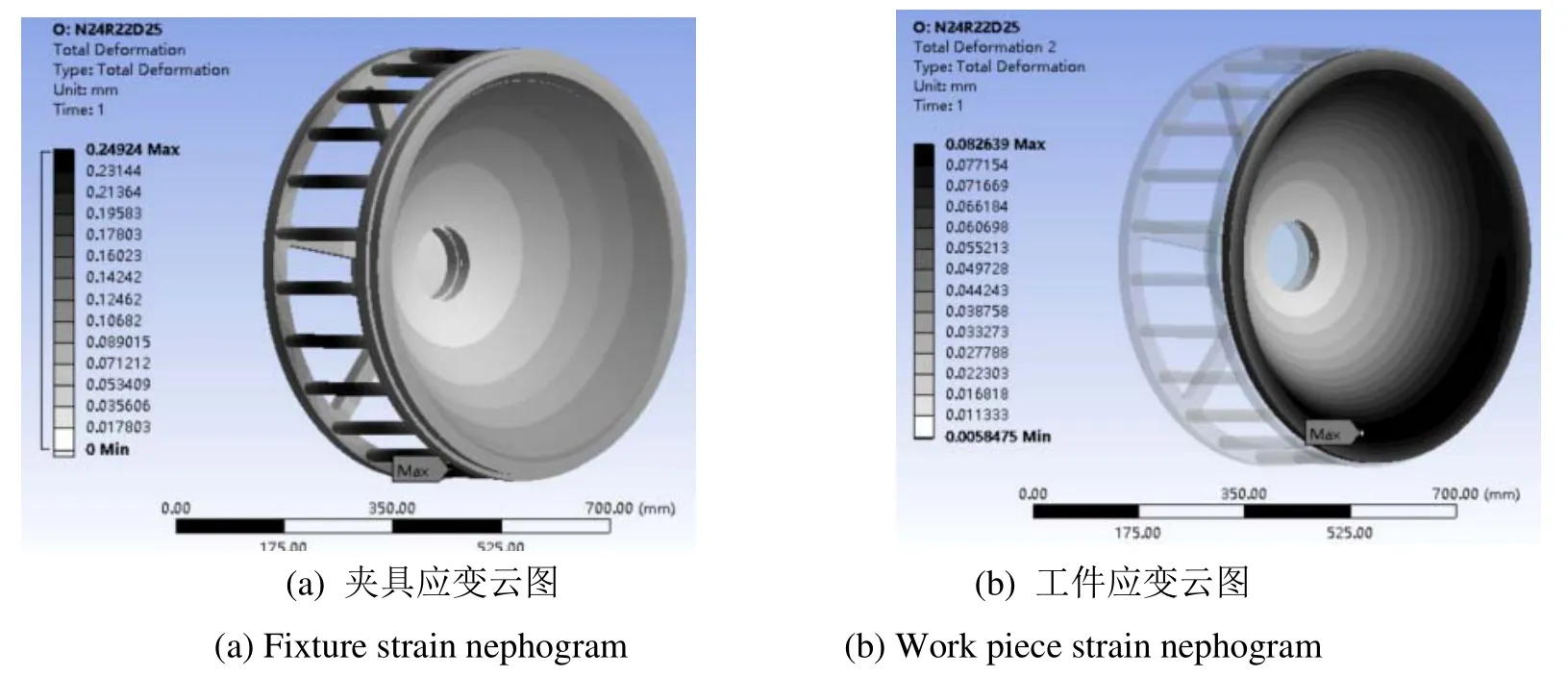
图8 夹具和工件应变云图Fig.8 Strain nephogram of fixture and work piece

2.3 加工实验结果

实验在MTC410 单点金刚石车床上进行，加工设备如图9所示，首先将铝反射镜安装于设计好的夹具中，将反射镜通过螺钉连接固定于顶板，并使其底部与夹具底板抵靠连接。再将整体通过螺栓连接固定于机床主轴。其次，将变换后的[X,Z,B]三轴加工坐标程序导入机床程序系统，根据铝反射镜安装位置以及最佳拟合半径和刀具尺寸，设定加工坐标系原点。根据加工经验采用工件转速200 r/min，进给率4 mm/min，设定刀具工作台能够进行实时的平面移动和旋转，对工件进行加工。在单点金刚石非球面车削加工领域，最常用的加工面形精度Pv及表面粗糙度Ra检测设备为英国Taylor Hobson 公司生产的PGI 系列接触式轮廓检测仪。在本次加工中，使用该系列PGI1240 型轮廓检测仪进行Pv及Ra测量。此轮廓仪最大测量口径φ200 mm、最大测量弦高12.4 mm，属于此型轮廓仪标准配置。由于工件尺寸过大（口径φ682 mm，弦高220 mm），不能用该轮廓仪对工件进行直接检测。在我们加工实践中，对于工件直径或表面弦高超出轮廓仪测量范围的情形，通常采取局部测量外加可控的加工工艺过程来对工件最终加工精度进行控制，用此法加工出的产品多次在工程应用中得以成功验证，取得预期效果。对于能够直接测量工件局部的情形，在轮廓仪测量范围内对工件进行直接的局部加工精度测量，来对工件整体加工精度进行预测、控制；对于不能进行直接测量的工件，在轮廓仪测量范围内设计一个面形相同但口径小的调刀件，通过加工、测量和控制调刀件加工精度，来对实际工件加工精度进行预测、控制。在本次加工中，即是通过一个φ82 mm 的调刀件对实际工件进行加工精度控制。对口径为φ82 mm 的调刀件进行加工、检测，表面粗糙度值Ra约为10.1 nm，面形精度Pv约为0.6 μm。检测结果如图10所示。

图9 φ682 mm 非球面铝反射镜加工设备Fig.9 φ682 mm aspheric aluminum mirror processing equipment

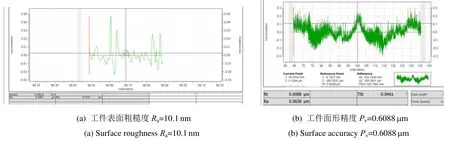
图10 非球面铝反射镜加工精度检测Fig.10 Machining accuracy test of aspheric aluminum mirror

3 结论

本文通过三轴联动加工方法对大口径非球面铝反射镜进行了单点金刚石车削，并对工件夹具进行了设计及参数优化。论文主要结论如下：

1）提出三轴联动加工方法，根据坐标变换原理，将水平X-Z两轴加工坐标转换为水平X-Z两轴以及刀具旋转的B轴的三轴加工坐标[X,Z,B]，解决了车床导轨行程和工作台台面回转容积受限问题，突破了单点金刚石车床加工大口径、大凹深非球面金属反射镜的难题。

2）设计大口径反射镜笼状夹具并分析夹具参数对整体变形的影响，结果表明，杆数对夹具最大变形量的影响最小，贡献率为0.7%；杆径和连接板厚度的贡献率分别为52.6%和31.6%。经过优化后的夹具参数组合为支撑杆的数量为24，支撑杆的直径为22 mm，上下连接板的厚度为25 mm。夹具最大变形量约为0.249 mm，工件最大变形量约为0.083 mm。

3）利用三轴联动加工方法对口径为φ682 mm 的非球面铝反射镜进行加工，对于φ82 mm 的调刀件，表面粗糙度Ra可达到10.1 nm，面形精度Pv可达到0.6 μm。所加工的φ682 mm 非球面铝反射镜产品达到用户使用要求。