基于多段式开挖的全尺模型边坡位移分析

袁材栋， 魏占玺， 薛 红， 谭维佳， 谢东武

(1.青海省环境地质勘查局， 西宁 611730； 2. 青海九零六地质工程公司， 西宁 611730； 3.长安大学地质工程与测绘学院， 西安 710054； 4. 同济大学土木工程学院， 上海 200092)

边坡监测是边坡风险预警的有效手段，以往的一般从土壤水分分布以及地下水位线演化规律进行分析，Wang团队研究发现降雨入渗存在饱和度阈值，而地下水位线会随之上浮[1-2]，也有研究对边坡变形方面进行长期监测，并提出一定的加固意见[3]。关于边坡位移和变形的测量，近年来伴随着信息与通信技术(information and communication technology，ICT)的发展，小型化的微机电系统(micro-electro-mechanical systems，MEMS)倾斜计，光纤传感器逐渐被使用，Liu等[4]提出方法可以在不降低检测性能的前提下节约能量消耗,减少了需要传输的数据量，验证了其系统的有效性。Uchimura等[5]基于水分计以及MEMS位移计对边坡进行长时间的检测，总结其变形趋势。也有研究在复杂地基中使用基于光纤传感智能监测系统，进行相关试验分析[6]。而使用全球定位系统(global positioning system，GPS)技术对露天矿山边坡的监测[7]，以及干涉雷达(interferometric SAR，InSAR)等非接触式位移测量方法[8-9]对于矿山边坡的实时监测也在不断被推广应用，其具备计算区域广，效率高等显著优点,当前也有着显著的发展。

基于边坡监测来预测滑坡的发生，设备测量只是一方面，更重要的是进行结果分析。较为典型的是通过边坡位移来预测崩塌的发生时间，该方法一般基于坡面位移发生速度与时间的经验式来进行崩塌预测。华开成等[10]将无人机低空摄影技术应用于高边坡开挖施工的质量智能化管理，并给出相应的智能化管理方案，设计了高边坡开挖施工的智能化管理流程，并对管理效果进行分析评价。孙树林等[11]利用有限元建立模型进行分析得到理论与实际相适用的结论。Varnes[12]和Voight[13]的研究表明，从开挖到边坡破坏，时间和位移的关系主要分为3个阶段：第一个为位移速率降低的蠕变阶段；第二个蠕变阶段位移速率保持恒定；而第三个阶段位移速率急剧增加。Hayashi等[14]利用模型实验结果对第三蠕变阶段变位量与位移速度之间的关系进行了对比验证，同时提出将第三阶段细分为两种模式。Iwata等[15]尝试通过大型模型试验数据预测边坡崩塌，并采用“正位移加速度”来定义第三蠕变阶段。降雨边坡模型实验中，坡面位移和剪切变形随着地下水升高而发生，并且地下水位和坡面位移，孔隙水压和剪切应变之间存在双曲线关系[16]，该研究表明边坡剪切变形随孔隙水压增加即应力变化而发展。为了适当预测由边坡中的应力变化而引起的变形，需要一种基于应力-应变关系来分析边坡的变形的方法。在挖掘或回填过程中，边坡内部应力随着形状的改变而发生变化，应力本身较难预测。Sasahara等[17]在降雨边坡模型实验中测量了坡面位移、坡面垂直向位移和坡内剪切位移并计算出相应应变值，结果表明，随着崩塌时间的临近，伴随边坡内剪切应变增加，垂直应变增加量几乎为0，在崩塌前维持定值。同样随着坡面位移增加，垂直向位移的增加量也随着崩塌的发生而渐近为0，即相对于剪切位移，垂直位移的变化量也被认为可以用来判定边坡稳定性。

为了探讨边坡开挖过程中垂直位移变化量是否可以成为判断边坡稳定性的标准，现以道路工程中的边坡挖掘施工为基础，构建一个全尺寸边坡模型，并从边坡下部进行多段式挖掘。记录和分析坡向位移和垂直位移的同时，将坡向和垂直向位移作为分矢量，进行合位移分析，并验证其判定边坡失稳的可能性。

1 研究方法

1.1 全尺寸边坡模型和测量装置

模型整体以及测量装置布设如图1所示。模型边坡用黏土制作，高3.5 m，宽4 m，倾角为30°，顶部水平长1.7 m。两侧壁为了减少摩擦，用聚乙烯板覆盖表面。提前计算好所需土体质量以及含水率，将制备好的样本自下而上分层制作，并分层放置传感器。并且分层进行压实，以确保完整性。土粒比重为2.679，平均湿密度为0.983 g/cm3，平均干密度为0.528 g/cm3，含水比88.7%，详细的物理参数如表1所示。通过压实试验得到最大干密度为0.682 g/cm3，最优含水率为98.7%，模型整体压实度为77%，粒径分布如图2所示。每一个观测点都安装两个位移计，以便记录坡面方向位移和其法线方向位移，研究中定义坡面下方移动和坡面下沉(压缩)为位移增加。

图1 测量装置分布Fig.1 Distribution of measuring devices

表1 物理特性Table 1 Physical properties

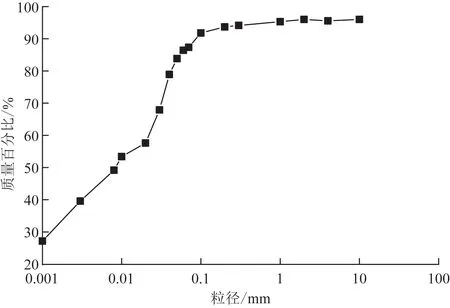
图2 粒径分布曲线Fig.2 Particle size distribution curve

1.2 试验方法

如表2所示，模型坡的开挖分8次进行。图3显示了每个开挖阶段后边坡侧面形状，如图1和图3(a)所示，第1～第3次开挖是以基准线1、2和3为目标，各挖掘倾角为60°。所使用的挖掘机铲斗宽度为1.8 m，分别从坡面中央，左侧，右侧顺序挖掘。第4和第5次分别以基准线3为目标，进行75°和90°挖掘。第6～8次挖掘中，对下方堆积的塌陷土进行了挖掘。

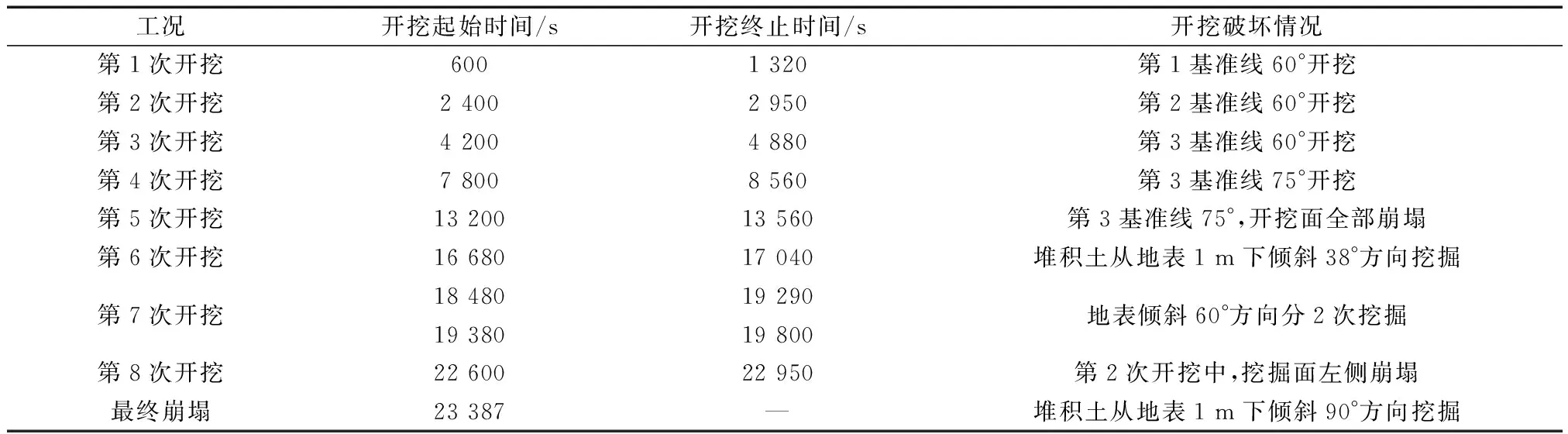
表2 挖掘阶段崩塌情况Table 2 Collapse during excavation

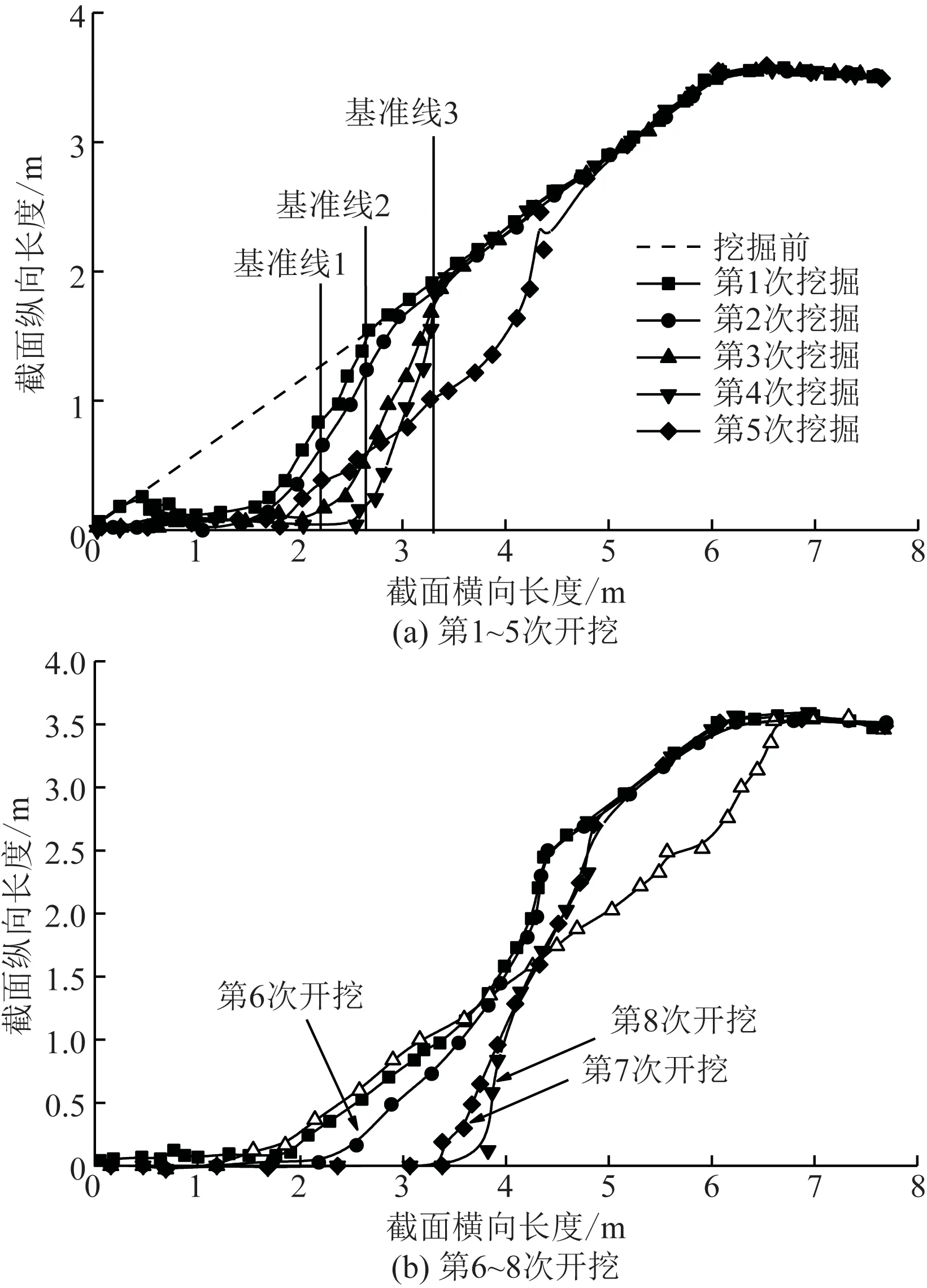
图3 模型边坡各开挖阶段以及侧面形状Fig.3 Each excavation stage and side shape of the model slope

2 试验结果

2.1 坡面方向位移

第8次挖掘后最终崩塌如图4所示，坡面方向位移随时间变化如图5所示。在第1～2次挖掘阶段几乎无变化，第3次挖掘开始时开始位移开始增加，之后也在持续增加。同样第4次挖掘开始到结束位移也在逐渐增大，并且大于第3次挖掘的位移增加量。第3次挖掘后，位移增加了约1 000 s并且增加量较小。第4次挖掘后，位移增加了4 000 s以上，位移急剧增大，位移量的大小按边坡中央，右下和左下的顺序递减，中央位移最大。第5次挖掘后，下部坡面塌陷。

图4 边坡最终崩塌形态Fig.4 The final collapse shape of the slope

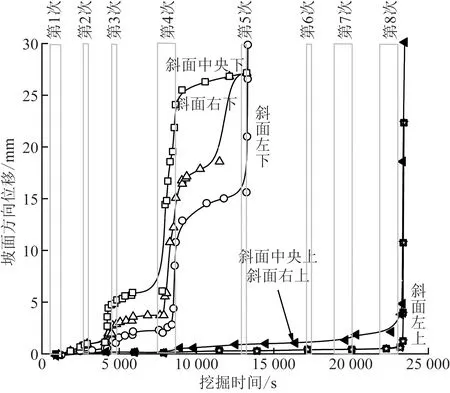
图5 坡面方向位移变化Fig.5 Displacement changes in slope direction

关于边坡上部的位移，在第4次挖掘后，在边坡的中心和右上开始略有增加，一直持续到第5次挖掘前。在坡面坍塌的第5次挖掘后，边坡上部的位移没有增加。可以认为第5次挖掘后，边坡下部挖掘面附近局部失稳并塌陷。第6次挖掘后，上部位移几乎没有增加，第6次挖掘后半段，中央和右上方位移略有增加。第8次挖掘开始，中央和右上方位移显著增加。左上方位移在第7次挖掘后增加不明显，第8次挖掘后显著增加，最终边坡崩塌。边坡下部中央部位移最大，边坡上部中央和右侧位移几乎相同，可能是由于侧壁摩擦的影响。第3和第4次挖掘后，在边坡形状不变条件下发生蠕变变形，单位时间内蠕变位移的增加随时间减小。边坡最终整体崩塌前也发生了蠕变变形，与边坡下部位移不同，单位时间内位移增加量逐渐变大。

2.2 沿垂直于地面的方向位移

图6为坡面垂直方向位移变化。边坡下部测得的位移中，第3次挖掘后中央位移显著增大。第4次挖掘后，右下方垂向位移持续增加，左下方减少表示此处坡面向上略微膨胀。第5次挖掘后，坡面坍塌导致垂向位移急剧增大。

图6 坡面垂直方向位移变化Fig.6 Vertical displacement change of slope

关于边坡上部位移，左上部垂直位移从第4次开始微增，其他直到第6次挖掘位置几乎无变化。中央和右上方在第6次挖掘后变化微小，但表现出膨胀现象。左上方在第7次挖掘后位移量也稍微增大，第8次挖掘后单位时间内左上、中央、右上方位移量显著增大，并在第8次挖掘后430 s左右边坡全体崩塌。

第4次挖掘后，垂直向位移单位时间内增加量逐渐变小，与坡面位移变现相同，但相对以坡面位移变化量要小得多。第8次挖掘后边坡上部垂向位移和坡面位移的增大都表现出加速现象。

3 坡面方向的位移与法线方向的位移之间的关系

3.1 边坡下部

边坡右下，中央下，左下方坡面向位移和垂直向位移关系如图7所示，相对于坡面位移平稳增加，垂直向位移在某时间表现为断续增加，此时间点被视为崩塌时间。崩塌后垂直向位移迅速增加，持续3 s左右。左下方直到坡面位移增加到5 mm，垂向位移为增加趋势。当坡面位移从5 mm增加到17 mm过程中表现为下降趋势，之后基本不变。中央下方坡面位移增加到8 mm左右，垂向位移保持增加，之后几乎恒定。右下方直到坡面位移增加到2.5 mm左右，垂向位移增加。坡面位移为2.5～7 mm的范围内，垂向位移保持恒定。7～15 mm垂向位移继续增加，之后继续保持定值。综上所述，边坡下部所有测量点的垂向位移在崩塌前表现为几乎不变。

图7 坡面方向位移和垂直方向位移关系(边坡下部)Fig.7 The relationship between the displacement in the direction of the slope and the displacement in the vertical direction (lower part of the slope)

3.2 边坡上部

边坡右上，中央上，斜面左上方坡面向位移和垂直向位移关系如图8所示，同边坡下部相同，垂向位移3 s左右急速增加。边坡左上方垂向位移随坡面位移增加而线性增大。边坡中央上方的垂向位移曲线在坡向位移到达 6 mm前表现为上凸，之后呈线性关系。以上垂向位移没有在崩塌前保持恒定。关于边坡右上方垂向位移，坡向位移到达4 mm时，垂向位移的增加量相对于坡面位移的增大逐渐减小，表现为上凸曲线，之后垂向位移几乎保持定值。综上所述，边坡上部只有右上部分垂向位移在崩塌前保持恒定，但左上和中央上部没有受此约束。

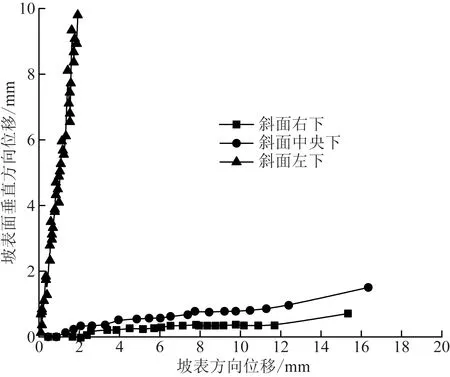
图8 坡面方向位移和垂直方向位移关系(边坡上部)Fig.8 The relationship between the displacement in the direction of the slope and the displacement in the vertical direction (upper part of the slope)

4 合成位移

根据先前的研究结果，边坡左上和中央上方在坡面方向位移增加的情况下，垂直方向位移增加但在崩塌前并没有停止增加，所以垂直方向位移在崩塌前并不全是恒定的。

4.1 合成位移与滑动面方向的关系

图9和图10分别表示坡面方向位移和滑动面上位移的关系。这里简化了土的变形：①剪切变形只在滑动面处发生，上部滑坡体默认为刚性；②假设坡面方向位移和滑动面上位移相等，由坡面方向位移S，垂直方向位移N得到合成位移R，合成位移R的偏角α由式(1)求得

图9 坡面方向位移Fig.9 The relationship between the displacement in the direction of the slope

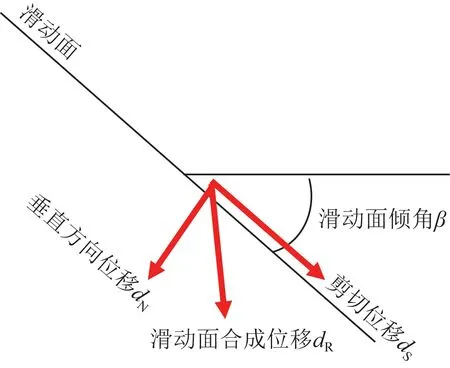
图10 滑动面上位移的关系Fig.10 the displacement on the sliding surface

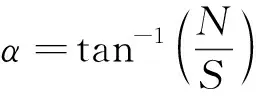
(1)

滑动面上合成位移dR由剪切位移dS和其垂向位移dN求得。当发生直接剪切时，一般随着剪切位移dS的增加，垂向位移dN减小，在崩塌前维持恒定。此时滑动面上的合成位移dR的方向与剪切位移dS的方向相同。由于滑动面上的位移增加，伴随坡面方向位移S增加，合成位移R与水平方向夹角(θ+α)逐渐接近于滑动面的倾斜角β，并且崩塌前θ+α=β即合成位移偏角α=β-θ。

坡面方向位移S增加，合成位移偏角α变化如图11所示。崩塌前α渐进于β-θ，当坡面与滑动面平行时，即θ=β，α=0，合成位移方向与坡面平行。坡面和滑动面不平行时，即合成位移方向与坡面不平行。垂直方向位移N在崩塌前不为0时，垂直方向位移的增加量ΔN根据式(1)以及坡面方向位移增加量ΔS，由式(2)表示：

图11 坡面方向位移S和合成位移偏角α的关系Fig.11 The relationship between slope direction displacement S and synthetic displacement deflection angle α

ΔN=ΔStana

(2)

此时，坡面方向位移S和垂直方向位移N关系如图12所示。边坡崩塌前坡面方向位移S和垂直方向位移N关系曲线近似倾角为α的直线。如图8所示，边坡中央上和左上方随坡面方向位移增加，垂直方向位移并没有保持定值，从而推测出坡面和滑动面不平行。如果崩塌前α=0，则坡面与滑动面平行且垂直方向位移保持恒定。

图12 坡面方向位移S和垂直方向位移N的关系Fig.12 The relationship between the slope direction displacement S and the vertical direction displacement N

4.2 合成位移偏角随时间的变化

边坡下部合成位移偏角α随时间的变化如图13所示。边坡左下方偏角α在9 000 s前变化较大，之后至崩塌前趋于定值。中央下以及右下方偏角α在8 000 s前变化较大，之后变化较小中央下方逐渐减小，右下方逐渐增加。在第5次挖掘中，崩塌发生前所有位置的合成位移偏角α都减小了3°左右。边坡上部合成位移偏角α随时间的变化如图14所示。23 000 s左右所有位置的合成位移偏角α几乎没有变化，崩塌发生时α值在短时间内迅速减小或增大，之后区域恒定。

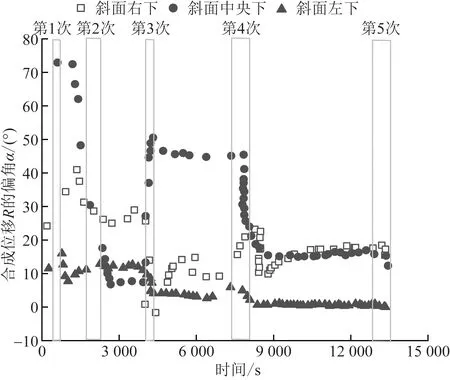
图13 边坡下部合成位移偏角α随时间的变化Fig.13 The change of the synthetic displacement angle α of the lower part of the slope with time

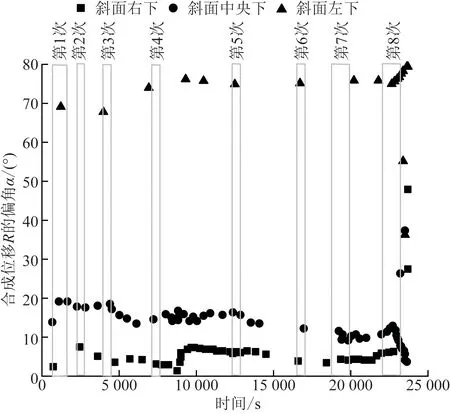
图14 边坡上部合成位移偏角α随时间的变化Fig.14 Changes in the synthetic displacement deflection angle α of the upper part of the slope with time

4.3 坡面方向位移与合成位移偏角关系

如上所述，合成位移偏角在边坡崩塌前短时间内迅速变化，同样可以看出坡面方向位移也在迅速增大。为了分析崩塌前短时间内边坡的状态，本节对坡面方向位移和合成位移偏角关系进行研究讨论。

边坡下部坡面方向位移和合成位移偏角关系如图15(a)所示。边坡左下方坡面方向位移至10 mm左右，合成位移偏角α逐渐减小。当坡面方向位移大于15 mm时，偏角α收敛为0°。边坡中央下方到方坡面方向位移为3 mm，偏角α显著增加，之后平滑减小。右下方坡面方向位移至7 mm左右，偏角α逐渐减少，之后至16 mm偏角α平滑增加。除了左下方之外，其余边坡下部合成位移偏角α最后都没有收敛。

图15 坡面方向位移和合成位移偏角关系Fig.15 The relationship between slope direction displacement and synthetic displacement deflection angle

边坡上部坡面方向位移和合成位移偏角关系如图15(b)所示。边坡左上方到崩塌发生坡面方向位移很小，位移至1.2 mm，偏角α保持递增。当位移为2.5 mm左右崩塌发生时，偏角α保持在78°左右恒定。中央上方坡面方向位移至8 mm左右偏角α减小，之后在4.5°～5.5°波动。右上方同样位移增加8 mm左右偏角α减小，最后恒定在2.0°～2.5°。综合以上，边坡上部随着坡面方向位移增大，合成位移偏角α最终能收敛为定值。

如上所述，边坡下部随着坡面方向位移的增加，合成位移偏角α平滑的增加或减小。相反边坡上部在崩塌前合成位移偏角α会收敛为定值。由于挖掘造成边坡失稳，模型边坡下部在第5次挖掘时崩塌，边坡上部在第8次挖掘后，蠕变变形增加最终崩塌。边坡上部位置由于蠕变引起的内部应力变化较慢，在崩塌前偏角α趋于恒定。边坡下部位置由于应力不连续变化以及崩塌等原因可能导致偏角α的不稳定变化。如同边坡上部蠕变崩塌的情况下，偏离角α的变化量接近0，边坡崩塌前近似于图11所示的状态。但如边坡下部内部应力突变的情况，今后仍需进一步讨论。

4.4 合成位移和滑动面的倾角

如图15(a)所示，除左下方合成位移偏角α约为0°以外，中央下和左下约为15°和18°。根据坡面倾角θ= 30°得到滑动面倾角β为45°～60°。从图5剖面图中观察，第5次挖掘后断面几乎与坡面平行，小于上面求得的45°～60°范围，推测是由于崩落土堆积导致。第1～3次挖掘面倾角为60°，与式(1)求得结果大致相同。关于边坡左下方求得滑动面倾角β为30°，与坡面倾角基本一致，即挖掘面方向上滑动面倾角不一定相同。

在边坡上部位置，崩塌前合成位移偏角α在左上方为78°，中央上和右上方分别为5°和2°左右。中央上和右上方合成位移方向几乎和坡面方向相同，滑动面平行于坡面。但左上方根据计算得滑动面倾角为108°，推断由滑动面形状不规则造成。

5 结论

通过对全尺寸模型边坡多段式开挖，以及多点坡面方向位移以及垂直方向位移的测定分析对边坡稳定性进行了讨论，研究结论如下。

(1)随着坡面方向位移的增加，一部分测量点坡面垂直方向上位移趋于恒定同时，部分点垂直方向上位移仍在波动。

(2)从合成位移与坡面方向夹角即合成位移偏角上分析，在发生蠕变的边坡上部，当坡面方向位移足够大时，合成位移偏角趋于恒定，相反在发生崩塌的边坡下部，合成位移偏角没有收敛。

(3)边坡下部计算得到的滑动面倾角为30°～60°，与挖掘面倾角相同。由于边坡上部合成位移方向与坡面方向几乎一致，求得滑动面与坡面倾角相同，但边坡左上方滑坡面倾角超过了90°。所以仅通过合成位移偏角来计算滑动面倾角，可能过于简单而导致误差过大，仍需进一步分析。