配电线路拓扑及台户区分自校验系统的研究
吴宗兵,董冉昊,廖 苏,张世权
(1.国网安徽省电力有限公司滁州供电公司,安徽 滁州 239000;2.湖北重光电气有限公司,武汉 437000;3.广州汉光电气股份有限公司,广州 510000)
0 引言
随着社会的发展,用户对电能供应和服务水平的要求不断提升,国家也高度重视低压用户的用电体验[1]。而一直以来由于技术和管理水平的滞后,中低压供电网络在建设和维护方面与输电网络相比仍然存在较大差距,这大大影响了电网发展的智能化,影响用户的用电满意度,增加了现场维护人员的工作量,因此,如果可以实现中低压台区拓扑关系的自动识别,全面获取台区内部信息,将其提供给运维人员,就能从根本上解决台区档案数据不准确的问题,从而实现营配系统末端融合,打造服务主动精准的智慧化台区,并基于获取的台区全量数据,实现大数据分析与应用,将大大提升线损治理效率,并可为生产、调控等提供数据支撑[2-3]。
针对上述存在的问题,文献[4]利用先进测量基础设施(AMI)获得的智能电流表的电压和电流数据,提出了一种时间序列相关法实现中压配电网的拓扑结构[4],该方法识别效率高,但成功率十分有限。文献[5]基于离群值检测、离散的弗里克距离和削波最近邻,提高了配电线路拓扑的校验精度[5],但是变电站区域仪表的样本数量少,同时也难以确定相关系数的阈值。
1 配电线路拓扑设计
针对上述技术存在的问题,本研究通过数据采集与监控(SCADA)系统和功耗信息采集系统得到配电数据,研究出一种基于智能电表电压曲线频域相似度的拓扑验证方法。
本研究的创新点在于:
(1)设计出一套配电网络拓扑自动校验系统,能够实现变电站故障信息的测量、计算与处理。
(2)构建出配电网线路模型,在配电网络中,能够通过配电站载波技术,获取总线到线路上的每个配电变压器信息,实现了配电站数据计算。
(3)利用随机森林模型进行对数据集进行预处理,剔除异常数据点,并构建出灰色关联分析模型,能够实现不同数据类型的关联计算。
基于上述描述,本研究设计了如图1所示的关键技术。确定了正确的线路拓扑结构之后,可以依靠集成的电量和线损管理系统来检测同一时期内线路的每日线损。当线损波动很大时,电压曲线用于计算配电网的电压降值,下游节点窃电的位置是通过电压的变化来实现的,正是这种变化导致窃电监控与识别的过程。
目前,拓扑建模的工作主要依靠人工维护。也就是说,模型应由维护人员预先在生产管理系统(PMS)或地理信息系统(GIS)中进行很好的维护,然后将其导入主站,这种人工方法的工作量很大,容易出现各种问题,例如,模型维护不及时,模型准确性低[6]。为解决该问题,本研究提出了一种通过电力线通信进行配电网拓扑建模的方法,以电力线为信息传输介质,建立具有距离信息的配电网拓扑模型。关于通过电力线通信的配电网络拓扑自动校验系统的体系结构如图1所示。

图1 配电网络拓扑自动校验系统
如图1所示,配电网络由1号线和2号线组成,两条线上有九个开关。其中,S0和S8是变电站出口断路器,S1,S2,S3,S5,S6和S7是普通分段开关,S4是接触开关,每个开关都配备有馈线终端单元(FTU)和电力线通信和传感(PLSN)设备。PLSN-M1是线路1的主要设备,PLSN-M2是线路2的主要设备,它们对应的端子称为边缘端子。PLSN10至PLSN12是线路1的从属设备,PLSN20至PLSN22是线路2的从属设备。PLSN-C12不仅是#1线路的从属设备,而且还是#2线路的从属设备,主设备在其自己的线路上包含其他从设备的地址[7-8]。关于配电线路拓扑构建过程如下:
第一步:主站将拓扑召唤命令发送到边缘终端,然后边缘终端获取并解析命令信息,其相应的主设备负责特定命令的执行。
第二步:主设备与从设备通信,获取从设备的对应的交换机ID,类型和状态信息
第三步:边缘终端将主设备获取的测距,设备类型,设备ID信息打包后发送给主站。
第四步:主站调用拓扑重构算法并构建拓扑模型,该模型可以用作其他高级应用程序的模型参考,除此之外,边缘终端还可以根据设置的时间参数定期进行建模工作。
2 拓扑校验方法
2.1 配电网络中的电压分布模式
在配电网络中,从变电站中的输出总线到线路上的每个配电变压器[9],电压分布可以将其视为树状结构,并将每个配电变压器视为一个末端节点,它是连接总线和末端节点的阻抗分支[10]。假设每个配电线由不同的总线配电,线路模型如图2所示。

图2 配电网线路模型
通过计算节点i处的电压得到公式(1)如下:
Ui=Uj+IZij=Uj+I(R+jX)
(1)
其中:Ui表示节点i的电压;Zij表示线路阻抗;R表示线电阻;X表示线电抗;I表示线电流。
在实际应用中,容量小于315 kVA的专用变压器和公用变压器是通过高压电源和低压仪表测量的,将低压侧的电压转换为线电压,然后将低压侧的线电压转换为高压侧。线路阻抗数据可用于查询电力生产管理系统(PMS)的数据,并可通过功耗信息收集系统的历史数据查询用户侧线路的特定部分的电流,这样,站点中的母线电压的标量值就可以由用户侧的测量数据和公共变压器的计量点来表示[11-12]。节点i的线电压可以从公式(2)获得:
(2)
本研究通过实际测量数据计算出站内总线电压与终端节点电压数据之间的相关性,从测量数据中选择6个测量点的T连接关系如图3所示。
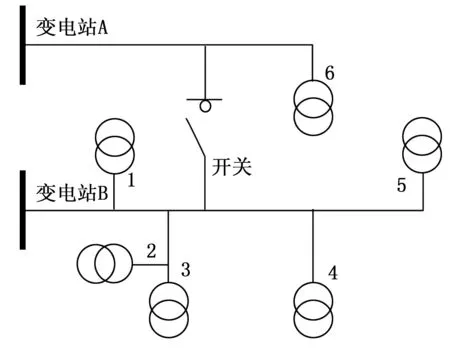
图3 6个测量点的T连接关系
在图3中,两个变电站A和B由不同的变电站供电,从两个变电站馈入的两条10 kV线路在同一塔上架设,在图中绘制了一个互连开关以进行区分,因此计量点6的电源很容易混淆[13]。
为此,本研究通过载波技术实现变电站电压的自动采样。载波技术的原理就是利用出站信号调制,在电压过零点前△T/2(过零点前30度)时刻,打开调制电路中的晶闸管,产生的瞬时电流耦合进工频电压的电流ie,引起一个电压降emod,在10 kV电压E过零点处发生畸变。电压畸变信号的编码是利用相邻两个周期电压波形来携带一位信息,利用调制位置的不同来表示“1”或“0”。入站信号调制方法与出站信号类似,只是入站信号调制是将畸变信号加于电压过零点时刻的电流上。关于调制等效电路与电压调制信号示意图如图4~5所示。
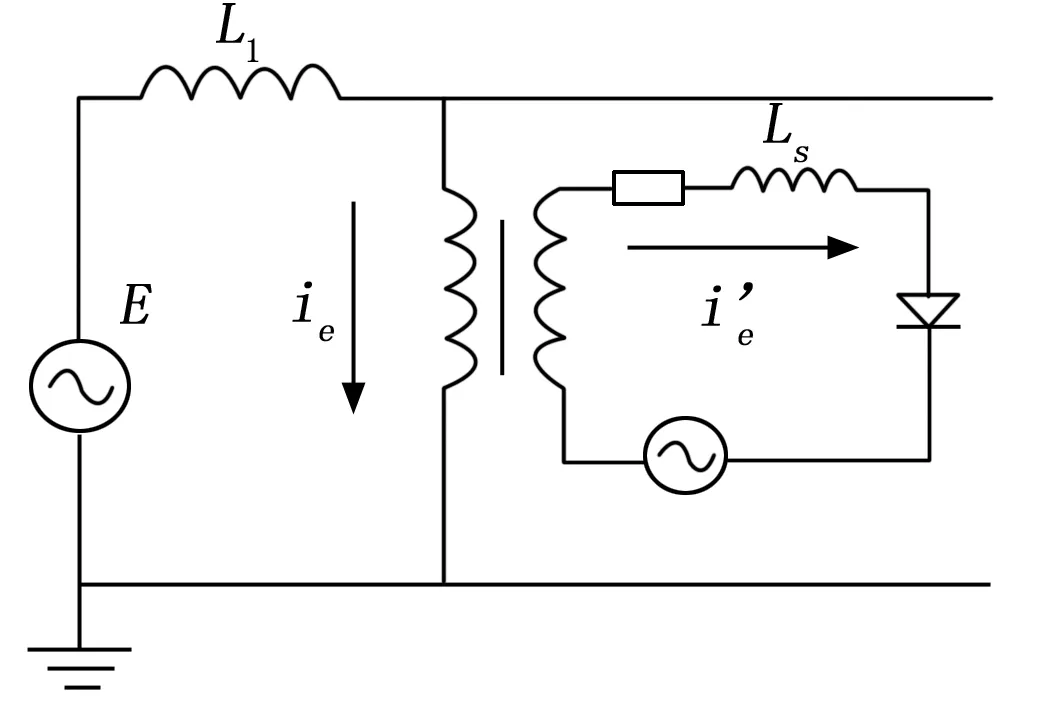
图4 调制等效电路

图5 电压调制信号示意图
通过载波技术得到第一天公交车和6个计量点的22小时电压曲线数据,并使用灰色相关分析和皮尔逊相关系数比较时域和频域的相关强度。
2.2 RF-GRA算法
在实际应用中,由于异常数据对判断准确率的影响很大,而智能电表采集得到的数据难免存在一些异常值,同时可能存在许多缺失值,采用传统灰色关联分析法(GRA)得出的结果偏差较大,因此需要考虑如何对电能计量数据进行预处理。本研究通过基于随机森林(RF)结合并优化传统GRA的新型算法RF-GRA,首先是RF预处理电能计量数据步骤:
计算任意电能计量数据检测点与孤立中心点之间的距离,其公式表示为:
‖x-yn‖=min(‖x-yn‖)
(3)
其中:公式(3)描述的是特征数据子样本集X中任意样本x与任意中心点yn之间的最短距离。
通过计算高压计量数据的平均值,整合处理监测点与中心点之间的距离数据,得出监测异常点方程组规则:
(4)
H(k)=ln(k)+γ
(5)
S(x,p)=2-H(x)/c(p)
(6)
其中:S表示异常指数函数,p表示中心点,c表示电能计量数据到中心点p的平均距离长度,γ表示欧拉常数,H表示调和级数。从公式(4)~(6)中可以得出,S异常指数函数值趋近于1,则判定监测点为异常数据。
之后,有关GRA方法的计算步骤概述如下:
1)通过RF筛选收集正常数据并分析数据,形成n个数据序列。
本研究的技术方案中,在频域中,有关灰色关联分析法的计算步骤概述如下:
(1)收集并分析数据,形成n个数据序列。
Xi=[xi(1),xi(2),…xi(m)],i=1,2,…n
(7)
其中:m是每一列中的数据数序号。
(2)确定参考顺序。参考序列可以是理想的比较标准,也可以根据评估目标选择参考序列。
X0=[x0(1),x0(2),…x0(m)]T
(8)
(3)数据的无量纲处理。每个数据列的物理含义可能不同,数据维数也不同,比较起来不方便,因此有必要对数据进行无量纲处理。
(9)
其中:i=0,1,2,…,n;k=1,2,…,m。
(4)计算绝对值。比较每个数据列中的最小值,然后从N个数据列中的最小值中取最小值min|x0(k)-xi(k)|,比较每个数据列中的最大值,然后从N个数据列中的最大值中取最大值max|x0(k)-xi(k)|。
(5)计算相关系数。分别计算每个比较序列和参考序列的相关系数η[14]。
(10)
其中:k=1,2,...M,分辨率系数ρ为0.5。
(6)计算关联度。关联度与比较级数一样多,关联度β的计算公式如下:
(11)
其中:i=1,2,...n。通过最终的灰色关联度,根据灰色关联模型检验等级标准,从而分析出配电网线路拓扑识别的准确性。关于根据灰色关联模型检验等级标准判别式如下:

(12)
通过上述灰色关联分析方法的计算,能够根据配电线路拓扑的不同数据因素,实现各种数据发展趋势相似或相异的计算,继而实现不同数据因素之间的衡量。
2.3 皮尔逊相关系数
在时域中,假设皮尔逊相关系数为r,其表达式为:
(13)

通过上述公式能够实现不同数据量之间的线性关系计算,提高了数据之间的关联计算能力,使得不同宏观思维数据关联性之间的数据产生直接的数据关系。
2.4 功率谱相似性分析
当两个离散时间序列中存在噪声时,通过直接比较两个序列的相似度,结果将受到噪声的干扰。本研究使用的解决方案是将离散时间序列变换到频域以降低噪声,并比较功率谱的相似度以测量两个离散时间序列的相似度[15-16]。功率谱定义为:
(14)
其中:x(n)表示随机信号,ejw表示复数随机变量,N表示电压曲线数据的数量。
通过上述公式的分析,将频域估计可分为经典频域估计和现代频域估计,而现代频域估计优于经典频域估计,本研究采用自相关方法实现自动回归(AR)模型参数频域分析,AR模型的功率谱估计是现代频域估计方法之一。AR模型参数的准确估计可以通过尤尔—沃克方程来解决。与电压曲线的相似性相比,只有有限长度的两组电压测量数据是已知的,该算法首先获得自相关函数的估计值,然后获得AR模型参数的估计值[17-18]。
3 实验与分析
3.1 实验构建与数据样本
根据智能电表在变压器区域收集的用户电压数据,选择用户最近一次的电压数据,形成电压序列。设置智能电表的采集时间为15分钟,则一天中有96个数据点。根据等式(13)计算不同用户的智能电表电压序列之间的相关系数,可以选择用于相似性判断的合理阈值r。当相关系数小于r时,可以确定用户的电压曲线与变压器区域的总体表不相似[19]。曲线类似于变压器区域的总体表,通过与计算机系统的用户档案信息进行比较,可以找出变压器区域之间的拓扑关系是否正确。根据GIS系统的数据能够获得用于验证变压器区域中的所有用户和相邻变压器区域中的所有用户的算法的样本集,其样本集中的字段和数据类型如表1所示[20]。

表1 测点字段和数据类型
对于实验环境,本研究采用JavaScript语言对SVG交互技术进行编码,所用的计算机操作环境为Windows10,64位,计算机的开发工具为Visual Studio2019,OpenCV3.0。计算机的硬件环境为CPU:Inter(R)Core(TM)i7;主频为2.59 GHz;内存16 G。所用的软件JavaScript的版本为ECMA Script 6。
3.2 拓扑检查的案例验证
在上文图3中,只有计量点1~5与总线B电连接,计量点6通过互连开关与总线B分开。为了测试算法的鲁棒性,此处添加了一个高压计量点7。它的电源是变电站C,而C的上部电源不同于A和B,将第一天每个计量点的22小时电压转换为高压侧,并通过MATLAB·2019仿真得到曲线图如图6所示。

图6 7个测量点的每日电压曲线图
分别在时域和频域计算灰度相关度和皮尔逊相关系数,得到表2、表3如下。

表2 母线电压和测点电压的灰色关联度
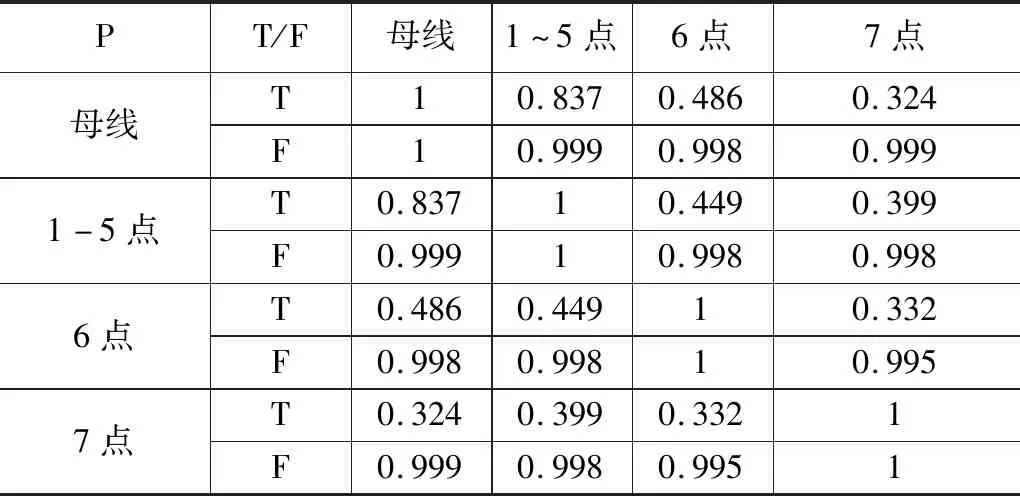
表3 测量点电压曲线的皮尔逊相关系数
从表2可以看出,总线电压曲线与计量点1~5电压曲线的灰色关联度大于计量点6和7,其分辨率高于22小时电压数据的分辨率,算法的鲁棒性提高,更加明显在频域。
对于配电线路T型连接的同一测量点,频域的灰色关联度在0.99以上,而没有电连接的测量点6和7的灰色关联度低于0.99。此外,本研究在该区域中添加了76条拓扑识别的12条线的测量点,以测试上述程度的正确性。发现76个测量点中的69个在频域上的灰色相关度表现相似,并且69个测量点中的每一个与其不同的母线电压曲线之间的灰色相关度值都在0.99以下,显然这提供了一种新方法用于检查配电线路的异常拓扑。
在表3中,母线电压和测量点6和7电压在时域上显示出良好的识别能力。但是,该算法错误地判断了测量点6与测量点1~5之间的相关性,因此在异常识别的鲁棒性方面,皮尔逊相关系数不如灰色相关性分析方法。在频域中,每条电压曲线的相关系数都接近于1。因此可以得出结论:与时域相比,频域不具有良好的鲁棒性,而且会增加误判的次数。
在得到上述结论后,本研究以某供电区域内3个不同小区的线路损耗波动异常的中压线为样本进行实际验证,并根据AR模型估算了电压曲线的功率谱,然后得出了功率谱曲线通过灰色关联分析进行了分析,统计结果如图7所示。
从图7的统计结果来看,A小区校验准确率最低,C小区校验准确率最高,达到99%。这是因为A小区建成年代较久,总用户数量最多,小区内配电线路线损严重,因此相对错误的用户数量较多。而C小区作为新小区,配电网设备以及线路处于非常健康状态,其相对错误用户几乎没有。
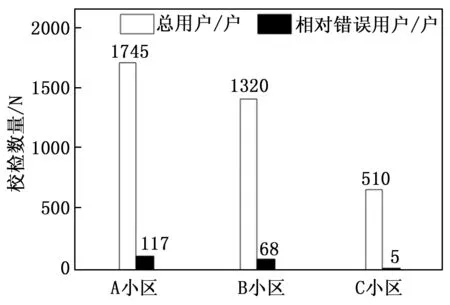
图7 3个小区校验结果对比
4 结束语
为了实现中低压台区拓扑关系的自动识别,本研究采用灰色关联分析和皮尔逊相关系数这两种算法在时域和频域上校验配电线路的拓扑结构。通过实例验证,发现频域灰色关联分析算法具有较强的鲁棒性和较高的准确率,可以识别出识别错误的用户,从而可以快速验证电网GIS系统的用户与站点中的变压器之间的拓扑连接关系的正确性。该检查方法人工成本低,准确性高,可操作性强,具有较高的应用价值。

