地铁站低频电磁噪声采集与特性分析*

邓羽捷 付天晖 王永斌 侯文达

（海军工程大学电子工程学院 武汉 430033）

1 引言

目前地铁站主要以有线通信方式为主，发生地质灾害时，存在因通信线缆损坏导致地铁站与外界之间通信中断的风险。低频无线电波可以穿透地铁站上方的地面实现与外界之间的双向无线通信，既可以在地质灾害发生时作为救援通信手段，也可以作为日常地面人员监测地铁站设备状态的补充手段，其示意图如图1所示。但由于地铁站存在多种用电设备，且车辆行驶时会辐射较强的电磁信号，因此地铁站与地面之间的低频无线电通信会受到强干扰，为解决这一问题，设计了地铁站低频电磁噪声采集系统，在武汉多个地铁站采集了电磁噪声数据，分别从时域、频域和统计特性等角度分析了噪声的特性，研究结果对于地铁站与地面之间的低频无线电通信系统的噪声特性、降噪方法研究，及提高通信的可靠性具有重要意义。

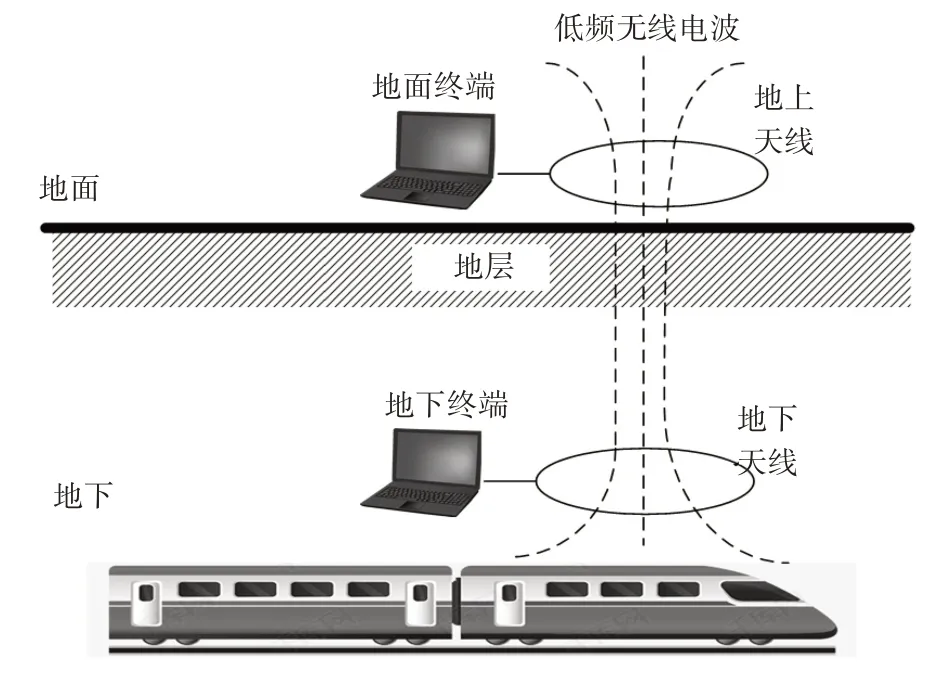
图1 地铁站低频无线电通信示意图

2 地铁站低频电磁噪声采集

为分析地铁站低频电磁噪声特点，制作了噪声采集系统。系统工作频段为DC-5kHz，接收天线采用铁氧体磁芯的磁性天线。由于感应到的磁场信号微弱，设计了增益可调的低噪声放大器以放大弱信号。采用NI USB-6361采集卡记录噪声，NI USB-6361是面向USB的多功能数据采集（DAQ）设备，兼容LabView软件，16路模拟输入通道，2两路模拟输出，可实现USB接口上的高性能读写。通过LabView编写了噪声采集与记录程序。以武汉地铁站为实验对象开展地铁站低频电磁噪声测量实验，表1为主要实验参数，图2为采集系统实物图。

图2 噪声采集系统实物图

表1 主要实验参数

将实测数据通过LabView软件保存为tdms格式，该格式数据可在Matlab中调用，图3为某地铁站无列车进站、列车进站、列车出站时的低频电磁噪声波形、功率谱密度及时频图。

图3（a）～（c）显示无列车经过噪声幅度不大，在采集频率范围分布均匀，时频图无明显特征，噪声能量均匀分布在1kHz～5kHz；图3（d）～（f）为列车进入站台，时域图存在明显的脉冲噪声，功率谱在1kHz～5kHz显著提高，出现强脉冲噪声时刻有明显的竖状条纹，则脉冲持续时间短能量高；图3（g）～（i）为列车出站，与进站相似，时域图存在明显的脉冲噪声，功率谱幅度显著提升，时频图有明显的竖状条纹，说明噪声具有较强脉冲特性。波形图显示列车到站和启动时，数据采集卡接收到尖锐的脉冲噪声，且幅度随着列车靠近站台时明显增加，远离站台递减。

图3 列车进站、出站及无列车经过时地铁站电磁噪声时域、频域、时频图

3 噪声统计特性分析

地铁站低频电磁噪声具有典型的非高斯特征，可采用非高斯模型描述统计特征。非高斯模型分为物理和经验模型，物理模型以Middleton模型［2］为主。1925年Paul Lévy提出Alpha稳定分布［3］；1995年Nikias提出稳定分布可描述脉冲噪声［4］，较Middleton模型复杂度低。本文结合实验和仿真验证，尝试采用Alpha稳定分布描述地铁站低频电磁噪声统计特征。

3.1 Alpha稳定分布及其参数估计

Alpha稳定分布没有统一封闭的概率密度函数表达式，可由特征函数表示［5］，通过傅里叶反变换积分定义对称Alpha稳定分布概率密度函数，α、β、γ、δ是决定分布的四个参数：

稳定分布参数估计方法有极大似然法（MLE）［6～7］、样本分位数法（QM）［8］、特征函数法（CFM）［9～10］、极大值估计法（EVM）［11～12］、分数低阶矩法（FLOM）［13］等，几种方法的特点如表2。

表2 几种稳定分布参数估计方法对比

极大值估计法能实时计算且保持高效率，具有鲁棒性。α、β、γ、δ估计值的表达式为

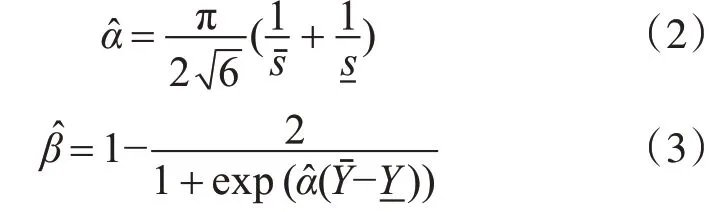
3.2 噪声幅度概率密度函数拟合

取地铁站噪声有效数据，根据3.1节的公式进行参数估计、高斯和稳定分布的拟合。设采集时间0.6s，长度6000，分为100段，第i段数据个数为60（i⊆L），表3为其参数估计。

表3中19m～33m深度增加α^略减小，则深度增加干扰幅度略增加，深度对参数估计影响小。建立稳定分布模型，图4为稳定分布拟合、原始数据、高斯PDF图及拖尾。

图4 Alpha稳定分布、原始数据、高斯PDF及其拖尾图

表3 Alpha稳定分布参数估计

结果表明，稳定分布PDF能较好拟合数据。为验证数据满足稳定分布，选取一段有效数据，进行无穷方差检验、Q-Q图、P值拟合优度检验、R_square值分析稳定分布的拟合度。

3.3 无穷方差检验

由于高斯分布存在有限方差，而Alpha稳定分布在α∈(0,2)不存在有限方差，因此观测样本方差是否存在可以作为判断是否为高斯分布的检验方法［5］。前n（n=1，2，…，N）个采样值的动态方差，其中，。图5为有效数据动态方差曲线。

图5（c）中样本数增加动态方差逐渐收敛，存在有限方差；6（a）和（b）样本数增加动态方差跳跃变化，不存在有限方差；表明无列车经过噪声满足高斯分布，有列车经过噪声不满足。

图5 样本方差随样本数变化曲线

3.4 Q-Q图检验

分位数图（Q-Q图）用来比较两个概率分布分位数，是判断随机变量高斯或非高斯的一种简单直观的方法［14］。将分布和样本的分位数分别表示为横纵坐标，绘制Q-Q图如图6所示。

图6（a）为无列车经过噪声与高斯分布Q-Q图，十字线与虚线偏差很小，分布在一条直线上，理论分位点一致，则该数据符合高斯分布；图6（b）为列车经过噪声与高斯分布Q-Q图，十字线与虚线两端出现严重偏离，则数据不满足高斯分布；图6（c）为列车经过噪声与稳定分布Q-Q图，十字线与虚线偏差不大，理论分位点一致，则数据满足Alpha稳定分布。

图6 样本数据与所选分布分位数图

3.5 基于特征函数的P值拟合优度检验

如前所述方法的标准都是观察法，简单直观，但没有确定性指标，缺乏依据表明数据满足分布；本文引进一种统计假设检验方法——基于特征函数的拟合优度检验［16］，步骤如下。

1）建立原假设H0：噪声有效数据符合Alpha稳定分布和备择假设H1：噪声有效数据不符合Alpha稳定分布，显著性水平为5%；

2）根据有效数据Xk(k=1,2,…,N)和分布模型计算其特征函数和；

4）μ=0.05,t∈[-5,5]，计 算；计算时，=1；Wj-Wa≤0时，=0；

5）将P值与显著性水平对比，判定是否接受原假设。

表4为各段数据P值及平均值。各组平均值均大于显著性水平，则判定接受原假设，即噪声数据符合Alpha稳定分布。

表4 各组有效数据的平均P值

3.6 R_square（确定系数）指标

R_square用于检验模型，接近1则解释能力强，模型对数据拟合得好［16］，计算公式为

yi为有效数据，为拟合值，为有效数据平均值。表5为列车经过噪声与模型的R_square。

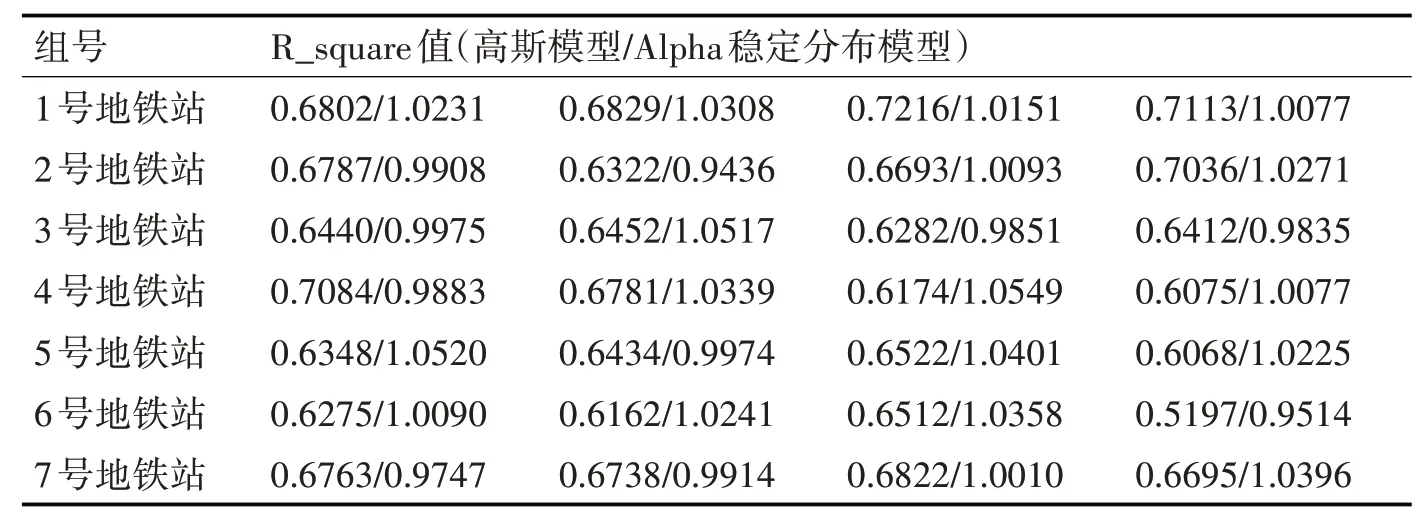
表5 有效数据与高斯/Alpha稳定分布的R_square值

列车经过站台时稳定分布R_square值接近1，表明稳定分布的拟合效果比高斯模型好。

4 结语

为实现地铁站与外界的低频无线电通信，本文采集了地铁站电磁噪声，从时域、频域和统计域分析了噪声特性，提出用Alpha稳定分布描述噪声统计特性、极大值法估计参数，对比PDF、无穷方差、Q-Q图、拟合优度检验、R_square分析稳定分布的拟合度，结果表明：

1）地铁站电磁噪声主要由脉冲与高斯噪声混合组成，无列车经过时主要为高斯噪声，列车进出站时主要为脉冲和高斯噪声的混合，脉冲幅度随列车靠近站台增大，远离站台减小；

2）在采集频率（1kHz～5kHz）范围内，地铁站噪声在频域分布均匀，无明显的“线谱”成分，当地铁进出站时噪声能量增强，无列车经过时噪声能量较弱；

3）地铁站深度对噪声特性影响不大，噪声PDF为“尖峰厚尾”，满足Alpha稳定分布。