基于检验测试的安全仪表系统安全评价Markov简化模型
姬 康,王 璐,王明锋,王先朝,许 鹏,刘晓亮
(1.中国石油新疆油田分公司呼图壁储气库作业区,新疆 呼图壁 831200;2.机械工业仪器仪表综合技术经济研究所,北京 100055)
安全仪表系统(Safety Instrumented System,SIS)是用来实现一个和多个安全功能的系统,在发生事故时能够将工艺过程或生产装置切换至安全状态,起到防止危险发生或减轻事故后果的效果,最终能够保证人员、设备和环境的安全。本文仅限于在低要求运行模式下的SIS,要求时危险失效平均概率(the average Probability of dangerous Failure on Demand,PFD
)是SIS的安全性量化的重要指标,通常要求频率小于每年一次。PFD
受系统架构、系统中组件的故障率、平均故障诊断时间、维修恢复时间、检验测试时间间隔等因素的影响,可以通过提高系统中组件的可靠性、增加冗余通道、缩短检验测试时间间隔、增加部分检验测试等方式,来降低PFD
的值。在SIS整个安全生命周期中,运行维护阶段占了较大的比例,关于SIS的运行特性和生产维护对其安全性造成的影响已有大量的相关研究,提出了众多计算方法。如IEC 61508-6标准中提出了常用冗余系统的简化计算公式,但该系列公式只涵盖了SIS安全性分析中的少数因素;Innal等分析了部分检验测试的影响,给出了一个基于1oo2系统的Markov模型简化公式;Wu等考虑了故障率的韦伯分布,利用条件概率理论,提出了SIS不可用性计算公式;Signoret等建立了一个以可靠性框图为驱动的Petri网安全分析模型。随着工艺自动化程度越来越高,SIS本身结构和运行维护日益复杂,安全性的动态特征越来越明显,针对由于组件故障和检验测试而导致系统安全性随时间变化的冗余系统来说,IEC 61508-6标准中推荐使用Markov模型和Petri网。Petri网能够对SIS安全性进行较为准确的评估,但是由于Petri网生成的模型使用起来难度较大,安全分析师往往需要深刻地了解Petri网建模原理才能建立计算模型。Markov模型相比Petri网较为简单,具有较高的灵活性和能够覆盖多种场景的特性,被认为更适合用于SIS在动态环境中的定量评估。然而,当在Markov模型中引入新的组件和因素时,其状态数量会呈指数增长。鉴于这一局限性,通过分析系统结构特征,将Markov模型进行简化的方法得到了广泛的研究。如Stewart提出了状态合并的思想来简化Markov模型;Xu等使用图形合并的方法将高阶Markov模型近似简化为低阶Markov模型;Guo等提出了合并具有相同转换率状态的方法来简化Markov模型;Chen指出可以通过删除停留时间较短状态来简化Markov模型;李鹏等在传统Markov模型的基础上,考虑周期检测策略,对SIS的安全失效概率(Probability of Failing Safety,PFS)进行了评估;王海清等综合考虑检验测试、冗余结构和系统失效等因素,提出了多阶段马尔可夫模型简化算法。本文在上述研究的基础上,提出了一种基于检验测试的要求时危险失效平均概率(PFD
)的Markov简化计算模型,适用于常见同构冗余架构系统的SIS,并以1oo2冗余架构系统为例对Markov简化模型进行了详细的分析说明,该Markov简化模型主要包括确定状态间转换率、删除停留时间较短的状态、合并具有相似特征的状态,并利用参数灵敏度分析引入模型修正因子。1 安全仪表系统(SIS)失效分类
安全仪表系统(SIS)失效可分为危险失效、安全失效和无影响失效,能够引起危险事件的失效称为危险失效,能够引起误停车的失效称为安全失效,无影响失效不参与失效率计算,可能会造成潜伏故障。PFD
只与危险失效相关。危险失效被分为可诊断到的危险失效(dd)和不可被诊断到的危险失效(du)两种类型。其中,为了减少由于du类型失效导致的系统不可控时间,最常用的方法是增加部分检验测试的频率。考虑部分检验测试,du类型失效又被分为两类:一类是可被部分检验测试发现并进行恢复的失效,称为PT类型失效;另一类是仅可被完全检验测试发现并恢复的失效,称为FT类型失效。假设系统总体失效率为λ
,危险失效率为λ
,安全失效率为λ
,dd类型失效率为λ
,du类型失效率为λ
,PT类型失效率为λ
,FT类型失效率为λ
,诊断覆盖率为DC
,部分检验测试可检测到失效的能力为θ
。它们之间的关系如图1所示。
图1 安全仪表系统(SIS)失效率分类Fig.1 Classification of failure rate for Safety Instrumented System (SIS)
2 Markov简化模型
2.1 基于Markov的PFDavg计算模型
本文以应用较为广泛的1oo2冗余架构系统为例对Markov模型进行简化说明。假设部分检验测试时间间隔(T
)在完全检验测试时间间隔(T
)内定周期分布。如图2所示,建立了基于1oo2冗余架构系统的Markov安全分析模型,此模型没有考虑部分检验测试。其中:状态用圆圈表示,转换率用箭头表示;在状态圈中,下半圈中标注的是状态的索引值,上半圈中序号1对应的是先发生的失效类型,序号2对应的是后发生的失效类型。
图2 基于1oo2冗余架构系统的Markov安全分析模型Fig.2 Markov safety evaluation model for 1oo2 redundant architecture system注:OK表示正常工作;dd表示已产生dd类型失效;du表示已产生du类型失效;μdd表示一个dd类型失效的恢复率;μ1、μ2表示不同状态之间的转换率。下同。
如图3所示,建立了包含部分和完全检验测试的1oo2冗余架构系统的Markov安全分析模型。

图3 包含部分和完全检验测试的1oo2冗余架构系统Markov安全分析模型Fig.3 Markov safety evaluation model for 1oo2 redundant architecture system (with partial and entire test)注:FT表示已产生FT类型失效;PT表示已产生PT类型失效;μ1~μ6表示不同状态之间的转换率。
由图2和图3可见,在考虑部分和完全检验测试对SIS的影响时,Markov模型的状态数量从6个变为了11个。可见,考虑因素的增加会导致状态数呈指数增长,这是在安全性分析中使用Markov模型的主要局限之一。因此,在计算结果的误差能被接受,并且保留Markov模型动态特性的前提下,对Markov模型进行简化,可以有效提高建模和计算效率。
2.2 Markov模型的简化步骤
Markov模型的具体简化步骤如下:
(1) 简化第一步:确定转换率μ
。假设V
≪U
≪μ
,其中V
={λ
、λ
、λ
},U
={μ
,μ
,μ
,μ
,μ
,μ
},从稳态不可用度和瞬态不可用度两个角度,得出各状态的PFD
计算公式,以此来计算各状态之间的转换率。其中:
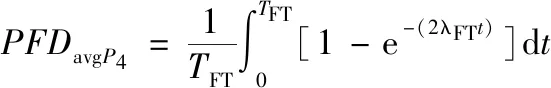

(1)

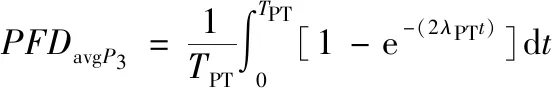

(2)
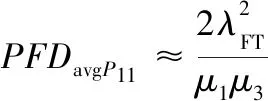

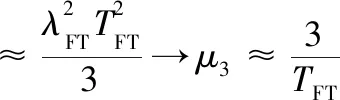
(3)

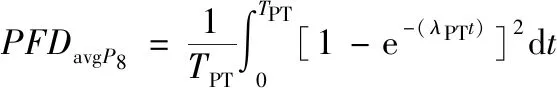

(4)



(5)
在计算μ
时,因为状态10是先发生FT类型失效,后发生PT失效,系统不工作的时段无法确定,只依赖于状态10很难列出瞬态方程式,因此将状态9和状态10合并,列出基于此两种状态的瞬态和稳态不可用度的方程:




(6)
其中:T
=mT
;m
为部分检验测试定周期分布因子;j
为单个部分检验测试的索引值;t
为时间积分变量。(2) 简化第二步:确定主导状态。对于冗余系统来说,若系统由n
个独立通道构成,且在要求发生时至少有k
个通道能正常执行安全功能,则系统PFD
是(n
-k
+1)个已失效通道状态的PFD
之和。对于1oo2冗余架构系统来说,就是2个通道失效状态的PFD
之和,即:
(7)
式中:l
为各状态的索引值。利用各状态基于稳态不可用度的PFD
计算公式,计算与系统PFD
相关的各个分状态的PFD
,表1给出了各个分状态PFD
的计算结果,其中相关安全数据来自OREDA数据库。根据公式(1),可计算得到系统PFD
为1.143 3×10。
表1 Markov模型的计算结果Table 1 Results of the Markov model
由表1可知,状态5、6和7对系统PFD
的权重较小,可以发现这些状态(5、6和7)都与λ
相关,是能够被在线诊断检测出的状态,因为在线诊断的间隔时间较短,所以在此状态的停留时间也较短。由于停留时间较短的状态对Markov模型计算结果的影响不大,因此在Markov模型简化过程中,可将此类状态从Markov原始模型中删除。另外,状态2与系统PFD
的计算无关,也可将其删除,从而得出如图4所示的Markov初步简化模型,表2给出了特定安全参数下Markov原始模型与Markov初步简化模型的计算结果。
图4 Markov初步简化模型Fig.4 Preliminary simplified Markov model

表2 特定安全参数下Markov原始模型与Markov初步简化模型计算结果的对比Table 2 Comparison of the results between original Markov model and preliminary simplified Markov model with certain safety parameters
由表2可知,Markov原始模型与其初步简化模型在PFD
的计算中结果非常接近,表明从Markov模型中删除停留时间较短的状态不会对计算结果产生较大的影响。(3) 简化第三步:合并特征相似的状态。系统PFD
是状态8、9、10、11的PFD
之和。将公式(1)~(6)代入各状态的稳态公式。其中,状态8和状态9的稳态方程式相似,故在公式中可将其进行合并。有:
(8)
分析公式(8),此公式与由挪威工业科技研究院(SINTEF)采用PDS方法给出的如下公式相似:


(9)

T
内,即此种状态可被部分检验测试修复到系统不失效的状态。此类状态对应的公式为
(10)
(2) 全部失效为FT类型失效的状态。即此种状态可被完全检验测试修复到系统不失效的状态。此类状态对应的公式为

(11)
(3) 首个失效为FT类型失效,在n
-k
+1个失效中包含有PT类型失效的状态。此类状态受连续发生FT类型失效的个数影响,假设首先连续发生了s
(s
<n
-k
+1)个FT类型失效后,发生PT类型失效。前s
个FT类型失效对应的平均系统不工作时间是以T
为基础的,在PT类型失效发生后,系统失效一定发生在部分检验测试时间间隔T
内,这与(1)中描述内容相同,计算首个PT类型失效对应的系统平均不工作时间时,假设完全检验测试时间间隔比部分检验测试时间间隔大很多,可以忽略FT类型失效数量,近似看作发生s
=1个FT类型失效后发生PT类型失效的系统平均不工作时间。此类状态对应的公式为

(12)
其中:1≤s
≤n
-k
;1≤g
≤max(1,n
-k
-s
);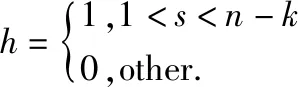
PFD
等于相关各分状态的PFD
之和,可表示如下:PFD
=PFD
avg+PFD
avg+PFD
avg


(13)
其中:1≤s
≤n
-k
;1≤g
≤max(1,n
-k
-s
);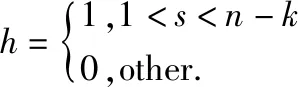
3 Markov简化模型修正因子分析
与Markov原始模型相比,其简化过程通常会导致公式的计算结果有偏差。通常对于Markov简化模型,可以用以下公式进行修正:

(14)
C
是修正因子,在此用于最小化Markov简化模型与Markov原始模型计算结果的偏差。本文通过欧几里得距离来导出多个安全参数在置信范围内两模型之间的相似度,并利用各安全参数对PFD
的权重影响,确定整体C
。3.1 修正因子分析指标
影响修正因子的因素有相似度、相对误差和参数灵敏度及其权重值。利用欧几里得距离来比较Markov原始模型与Markov简化模型绘制的两条曲线之间的相似度。相似度定义如下:

(15)
式中:x
为选定的安全参数;(a
,b
)为相关安全参数的置信区间。ED
的取值范围为(0,1],ED
值越小,两条曲线越相背离,越接近于1,相似度越高;如果两条曲线完全吻合,则ED
值为1。在给定范围(a
,b
)内,按下式计算基于选定安全参数的Markov原始模型与Markov简化模型PFD
的相对误差(RE
):
(16)
RE值不宜超过15%,否则认为模型不可信。同时,记录PFD
的最大偏差(即PFD
的最大值和最小值),并根据PFD
值的变化,来度量该安全参数的灵敏度及其权重值。灵敏度定义如下:
(17)
其中,Δx
≤(b
-a
),x
∈(a
,b
)。该安全参数的权重值计算公式如下:

(18)
3.2 基于安全参数的修正因子分析
针对不同的冗余架构系统,修正因子C
是不同的。在1oo2冗余架构系统中,当分析选定安全参数x
对PFD
的影响时,假设其他安全参数是恒定值,函数方程为:PFD
=f
(x
),x
∈(a
,b
),在给定范围(a
,b
)内,通过插值计算得出本安全参数x
对应的最佳C
值,该最佳C
值能够使得Markov简化模型与Markov原始模型的相似度ED无限接近于1,并且两模型PFD
之间的相对误差小于15%。将λ
作为选定安全参数,设定λ
的置信区间为(10h,10h),其他安全参数为恒定值,经过插值计算表明:当C
=1.910 7时,Markov原始模型与Markov简化模型之间的相似度最高,ED
值为0.999 986;两模型PFD
之间的最大相对误差RE
为5.40%,PFD
的最大值和最小值分别为6.924 1×10和7.398 2×10,见图5。
图5 基于λdu的PFDavg趋势图Fig.5 Trend curves of PFDavg based on λdu
将DC
作为选定安全参数,设定DC
的置信区间为(0.2,0.8),其他参数为恒定值,经过插值计算表明:当C
=1.965 4时,Markov原始模型与Markov简化模型之间的相似度最高,ED
值为0.999 997;两模型PFD
之间的最大相对误差RE
为1.57%,PFD
的最大值和最小值分别为1.171 0×10和1.143 2×10,见图6。
图6 基于DC的PFDavg趋势图Fig.6 Trend curves of PFDavg based on DC
将θ
作为选定安全参数,设定θ
的置信区间为(0.
2,0.
8),其他参数为恒定值,经过插值计算表明:当C
=1.944 1时,Markov原始模型与Markov简化模型之间的相似度最高,ED
值为0.
999 995;两模型PFD
之间的最大相对误差RE
为3.68%,PFD
的最大值和最小值分别为2.627 1×10和2.734 3×10,见图7。
图7 基于θ的PFDavg趋势图Fig.7 Trend curves of PFDavg based on θ
将T
作为选定安全参数,设定T
(h)的置信区间为(200 h,4 000 h),其他参数为恒定值,经过插值计算表明:当C
=1.959 7时,Markov原始模型与Markov简化模型之间的相似度最高,ED
值为0.999 999;两模型PFD
之间的最大相对误差RE
为0.41%,PFD
的最大值和最小值分别为2.012 3×10和1.051 4×10,见图8。
图8 基于TPT的PFDavg趋势图Fig.8 Trend curves of PFDavg based on TPT
将T
作为选定安全参数,设定T
的置信区间为(4 000 h,24 000 h),其他参数为恒定值,经过插值计算表明:当C
=1.849 6时,Markov原始模型与Markov简化模型之间的相似度最高,ED
值为0.
999 963;两模型PFD
之间的最大相对误差为8.18%,PFD
的最大值和最小值分别为7.283 2×10和2.899 7×10,见图9。
图9 基于TFT的PFDavg趋势图Fig.9 Trend curves of PFDavg based on TFT
3.3 确定整体修正因子
为了计算整体修正因子,需要利用公式(17)和(18)确定模型中每个安全参数的灵敏度及其权重,1oo2冗余架构系统安全参数的权重分布,见图10。

图10 1oo2冗余架构系统安全参数的权重分布图Fig.10 Weight distribution of safety parameters of 1oo2 redundant architecture system
每个安全参数的单参数因子与该参数的权重值相乘,可得出单个参数修正因子。表3给出了基于1oo2冗余架构系统的单个安全参数修正因子的计算结果。将所有参数的修正因子相加,可得出1oo2冗余架构系统的整体修正因子C
,即C
=1.919 6。
表3 1oo2冗余架构系统的单个安全参数修正因子计算结果Table 3 Calculation of the correction factor of individual safety parameter for 1oo2 redundant architecture system
利用同样的的方法,可以计算出其他常用的冗余架构系统的整体修正因子,见表4。

表4 常用冗余架构系统的整体修正因子取值表Table 4 Values of correction factors for common 1oo2 redundant architecture system
3.4 修正后的计算公式
采用整体修正因子乘以Markov简化模型对应的公式(13),可得出不同冗余架构系统修正后的简化计算公式:
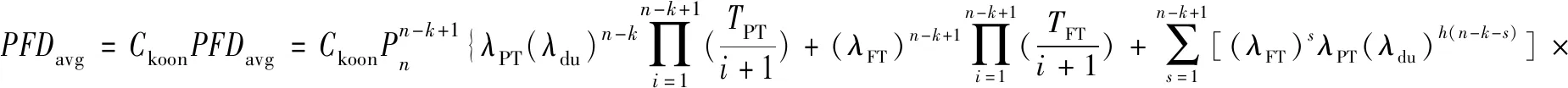
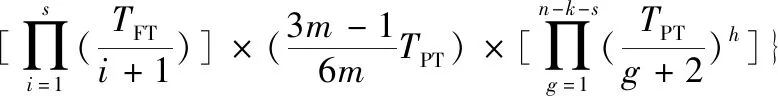
(19)
其中:1≤s
≤n
-k
;1≤g
≤max(1,n
-k
-s
);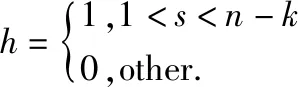
4 模型验证
以1oo2冗余架构系统为例,将本文导出的简化计算公式分别与Markov原始计算模型和IEC 61508-6中公式进行了对比分析。
如表5所示,列出了Markov原始模型一次迭代和Markov简化模型所需的实数加法器和实数乘法器数量,N
表示符号个数,可以看出在一定的置信区间内,简化计算公式的计算复杂度有显著降低。
表5 不同计算公式的计算复杂度对比Table 5 Comparison of computational complexity between different formulas
不同计算公式得到的PFD
结果对比,见表6。
表6 不同公式得到的PFDavg计算结果对比Table 6 Comparison of calculation results (PFDavg) between different Markov formulas
由表6可知:Markov简化模型与Markov原始模型PVD
的计算结果相比,平均误差小于5%;与IEC 61508-6中公式的计算结果相比,平均误差小于15%,这种偏差程度在评定安全完整性等级(SIL)时是可接受的。图11给出了Markov简化模型与IEC 61508-6中公式和Markov原始模型PFD
计算结果的偏差曲线对比图。由图11可见,Markov简化模型PFD
计算结果的偏差曲线与Markov原始模型在形状、趋势和大小上保持了高度的一致。
图11 Markov简化模型和IEC 61508-6中公式与Markov原始模型PFDavg计算结果的偏差曲线对比Fig.11 Comparison of deriation of PFDavg calculation result of simplified Markov model and formula in IEC 61508-6 from original Markov model
5 结 论
(1) 本文提出了一种基于检验测试的PFD
简化计算模型,适用于低要求运行模式下同构冗余koon架构系统的SIS。验证结果表明:Markov简化模型与Markov原始模型在主要特征上有很高的一致性,相对误差小于5%,可以应用于SIL等级的评估。(2) 本文在考虑了部分和完全检验测试的情况下,以1oo2冗余架构系统为例,详细说明了Markov模型简化分析过程,包括状态之间的转换率计算、主导状态的确定、相似状态的合并,并将安全参数放入一定的置信区间内,通过参数敏感性分析引入修正因子将计算误差最小化。

