一种新的量子行为衍生布谷鸟搜索算法

曲宝，李荟

（东北石油大学，大庆 163318）

布谷鸟搜索（Cuckoo Search，CS）作为一种群智能算法，目前已成为国内外的研究热点，最早是在2009 年由Yang 等[1]提出，主要通过计算机和数学模型模拟布谷鸟对幼鸟育雏时的自身特殊习性，同时仿照了鸟类的莱维飞行（Lévy flights）特性。该算法在数学模型描述过程中具有简单、参数较少的特点，并且非线性优化时的性能略高于一些常见的群智能算法[2-3]。因此，国内外很多学者将其应用于工程设计[4-5]、神经网络学习[6]、目标非线性优化[7]等问题。Lévy flights 属于随机游走模式，步长满足一个重尾的稳定概率分布。布谷鸟搜索算法采用小步长和大步长交替进行，最终实现随机游走的变量优化，完成算法收敛。Lévy flights 使得算法在早期寻优阶段可以确保种群的多样性，并增大变量空间的搜索范围；在后期，通过利用较大的步长确保算法能够逐渐收敛，完成全局最优解的计算。同时，通过Biased 随机走动辅助莱维飞行，有效完成全局与局部的优化计算和搜索平衡。很多学者对于布谷鸟搜索算法的研究，目前主要集中在自身算子的研究和算法融合两个方面，其中第一个方面包括Lévy flights[8]、Biased 随机走动[9]、逐维改进机制[10]、动态自适应发现[11-14]等。在算法融合研究方面，国内外的研究通过将布谷鸟搜索算法与其他群智能算法融合，文献[15-17]分别提出将该算法与粒子群、差分进化进行算子融合，改善算法的个体寻优策略，避免陷入局部最优。以上这些均较好的提升了CS 算法的收敛速度或求解质量。

量子计算是目前国内外广泛关注的一种先进计算理论，该理论应用到优化领域过程中，常将个体的实数或二进制编码采用量子比特表示，已被证明量子优化算法在种群的多样性和算法精度方面具有更强的优势[18]。文献[19]提出BQGA 算法，使用Bloch 球坐标实现三链编码，量子位具有两个转角参数，寻优能力优于其他基于单位圆的QEA 算法，但个体更新时未解决转角的协调问题，影响优化性能。文献[20]在此基础上提出QBEA 算法，引入量子计算理论，在Bloch 球面完成最短路径旋转，有效解决转角更新的调整量匹配问题，但存在以下问题：（1）进化算子中，所有个体的旋转幅角均采用的随机方式，有一定盲目性，未充分发挥最优个体的路标引导作用，进化速度较慢；（2）变异算子仅考虑多样性，未进行贪婪择优，个体进化经验丢失。

在之前研究的基础上，受布谷鸟搜索启发，提出一种量子行为衍生布谷鸟算法（Quantum-behaved Inspired Cuckoo Search，QBICS）。QBICS 采用Logistic混沌映射产生初始种群，使种群具有较好的多样性。根据量子计算理论，量子染色体使用Bloch 球面坐标描述，在更新时绕轴旋转，同时更新两个转角。全局搜索方面，使用当代最优解指导种群进化，根据莱维飞行计算量子比特逼近目标的旋转幅角。通过投影测量和解空间变化计算适应度，并进行贪婪择优。局部搜索方面，使用Biased 随机走动和差分项引入新个体，替换较差解。通过对全局最优解的Bloch 球面分布的证明，搜索范围缩小为Bloch 球面的半球搜索。在仿真实验中，通过四种常见的标准测试函数进行多种算法的非线性优化对比，实验结果证明，所提的QBICS 的寻优能力和优化精度有较为明显的提升。

1 标准布谷鸟算法

CS 中使用鸟巢代表求解问题的优化解，每次进化主要包括两个步骤：首先对当前解使用莱维飞行向最优解逼近，产生新鸟巢位置，并对二者贪婪择优；然后按照发现概率丢弃较差解，使用Biased 随机走动和差分项生成与丢弃数量相同的新解。

（1）莱维飞行随机走动

设Xg，i=（xi1，xi2，…，xm）为第g 代中第i 个鸟巢位置，得到的新鸟巢为：

其中，α 是步长，表示莱维飞行的搜索范围控制，利用寻优解与最优解的距离来完成，具体过程如下：

其中，α0为常数，Xbest为当前最优解。

式（1）中，⊕是点乘积，Leνy（β）是服从Lévy 概率分布的随机数。

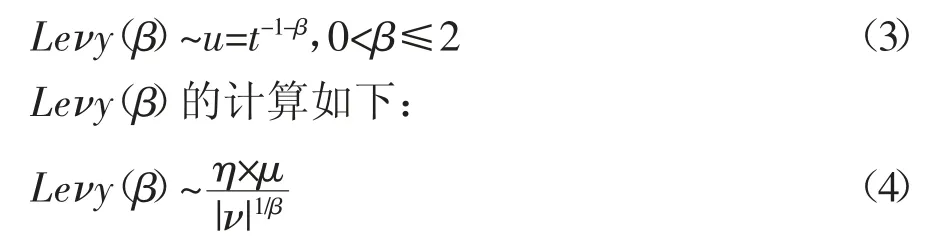
（2）Biased 随机走动

在当代种群中随机选择两个不同的个体，按下式生成新解。

其中，r 是缩放因子，是（0，1）之间的随机数，Xg，j和Xg，k是随机选择的两个个体。

2 量子衍生布谷鸟算法QBICS

2.1 Bloch 球面编码

根据量子叠加原理，在二维复希尔伯特空间中，一个量子比特可描述为：

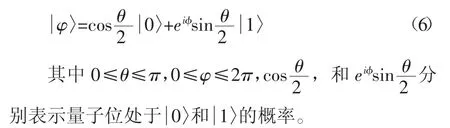
量子染色体表示待优化问题可行解，在QBICS中即为鸟窝位置。设种群规模为m，优化空间维数为D，第i 条量子染色体的编码方法如下：

在三维笛卡尔坐标系表示的Bloch 球面上，根据转角θ 和φ，可确定一个Bloch 球面点坐标p（x，y，z）=（cosφsinθ，sinφsinθ，cosθ），因此可用Bloch 球面上的点来描述量子比特，球面点和存在对应关系。

2.2 QBICS 的初始种群混沌初始化

在群智能算法和进化算法中，种群的初始多样性，即个体的搜索空间分布，对于算法的进化搜索过程中极为重要。混沌现象具有明显的随机特性，在自然界中普遍存在。在所提算法中，QBICS 采用了混沌理论中的具有虫口特性的Logistic 混沌映射方式，具体计算过程如下：

其中，uj=4 时进入混沌状态。种群初始化时首先随机生成D 个实数向量σ1=［σ11，σ12，…，σ1D］，σ1i∈（0，1）。令θij=σijπ，φij=σij2π，按式（7）产生第1 条量子染色体。再按式（9）依次生成m-1 组向量，同理产生其余m-1 条染色体。此时，种群中第2 条染色体的第1 个量子位为：

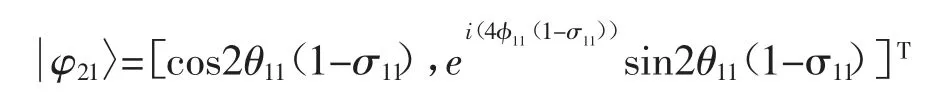
2.3 投影测量和解空间变换

其中Pauli 矩阵如下：

量子比特经投影测量后包含3 个数值，染色体包含3 条基因链，经解空间变换可分别代表3 组解，因此扩大算法的遍历范围。设第j 维变量取值范围为［min（j），max（j）］，解空间变换如下：

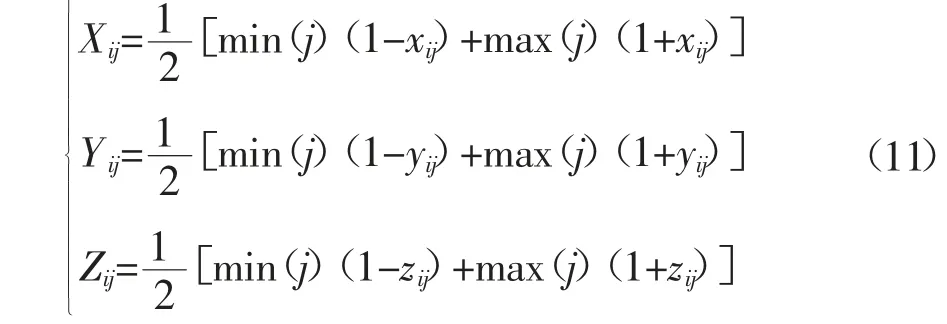
2.4 量子比特绕轴旋转

由于量子比特有两个转角，为避免两个转角分别进化，导致二者无法协同影响算法搜索效率的问题，QBICS 算法在Bloch 球面上建立搜索了机制，通过绕旋转轴旋转完成量子比特的θ 和φ 同时进化，通过量子位的投影测量直接得到Bloch 球面坐标，所经过的路径为Bloch 球大圆上的劣弧，实现两个参数调整量的最佳匹配，从而保证两个转角的调整具有更高的优化效率。

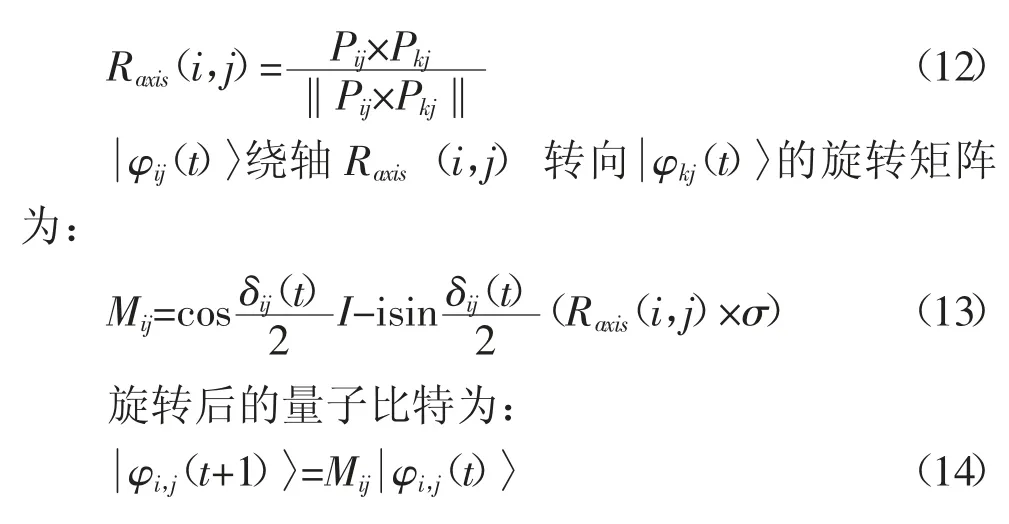
2.5 QBICS 的莱维飞行个体进化策略

量子比特在Bloch 球上绕轴旋转角度大小对算法性能较为重要，此外搜索区域对算法的进化效率也有一定影响。所提的QBICS 搜索范围可定义到Bloch 的上半球，减小球面搜索范围，提高搜索效率。因此QBICS 的Bloch 球面搜索范围限定如下：

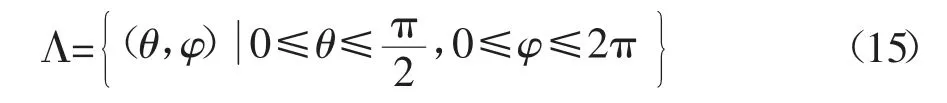
莱维飞行是一种服从Lévy 分布的随机走动策略，行走方式为短距离搜索和偶尔长距离搜索相间隔。对于进化过程，使用莱维飞行可有效增加种群多样性，搜索范围可以扩大，易跳出局部极值[1]。量子个体更新策略引入莱维飞行随机走动，确定量子比特向目标逼近时的Bloch 球面转角幅度大小。

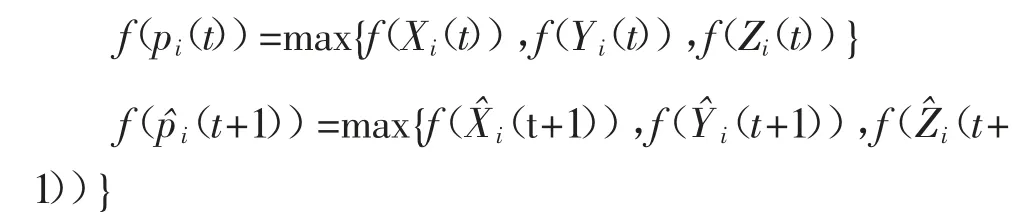
2.6 QBICS 的交叉变异策略

QBICS 算法的交叉变异策略仍采用Biased 随机走动方式计算，优化过程中根据种群的多样性和退化程度，自适应计算发现概率。初始化种群采用Logistic 混沌映射产生，具有较好的多样性，所有个体较为均匀的分布在Bloch 球面上，应减小丢弃较差个体的发现概率。此时进行交叉变异，势必会浪费一定的目标函数评价次数。当种群多样性降低时，为避免优化过程陷入局部，QBICS 增大发现概率，确保新个体的生成，从而提高种群多样性。

定义1 记种群在t 代的适应度为fit（t），历史平均适应度，则认为种群发生退化。

发现概率κc与种群的退化程度的关系如下：

若κc（0）=0.01，种群发生退化时的发现概率为单调递增且κc（t+1）∈［0.05，0.1］。

其中，λ 为缩放因子。计算pi（t）和pb（t）的旋转轴Raxis（i，b），根据式（20）计算pi（t）各量子比特的旋转角度，按式（14）将pi（t）绕轴Raxis（i，b）旋转，旋转后生成的新量子染色体为。最后按式（18）进行p（it）和的择优选择。

2.7 QBICS 的算法步骤

Step1 设置算法参数，包括种群规模n、量子编码长度D、Lévy flights 步长α0、发现概率初值κc（0）、迭代次数G；

Step2 t←0，根据Logistic 映射随机初始种群；

Step3 计算适应度。按式（10）、（11）进行量子位测量、投影和解空间变换，计算量子染色体适应度；

Step4 存储当代种群中的最优个体，并替换之前记录的全局最优个体，计算当代平均适应度fit（t）和历史平均适应度

Step5 个体莱维飞行进化。按式（17）计算旋转幅角，个体绕轴旋转产生新个体，通过贪婪策略择优；

Step6 按式（19）计算发现概率并丢弃较差解，按式（18）计算转角，生成与丢弃解数量相同的新个体，并贪婪择优；

Step7 t←t+1。若t≥G 或者达到计算精度，存储最优解，算法计算完。否则转Step3。

3 仿真实验

为验证所提算法的性能，采用标准的函数极值优化问题，并与标准的布谷鸟算法[1]（Standard Cuckoo Search，SCS）、Bloch 量子遗传算法BQGA[19]、Bloch 量子行为进化算法QBEA[20]进行对比。

3.1 测试函数

3.2 参数设置

对于前两个二维函数，4 种算法的种群规模m=20，最大迭代步数G=500，其中SCS 和QBICS 的α0=0.01、κc（0）=0.02。对比算法QIEA 的转角步长δ=0.01π、变异概率pm=0.05，对比算法BQGA 的转角初值Δθ0=Δφ0=0.02π。对于后两个高维函数，变量维数D=50，4种算法的种群规模m=30，最大迭代步数G=5 000，其他参数与前两个函数相同。

3.3 实验对比分析

实验环境：Matlab R2012a、CPU：i7-3770 3.4 GHz，内存4 G、win7-64。仿真实验过程中，为保证实验结果记录的客观性，实验对比的四种算法在相同实验环境下独立运行50 次。每次运行结束后，分别记录各个实验对比指标。其中，对于四种算法在函数f1～f4极值优化时的单步迭代运行时间见表1，收敛能力对比，包括收敛次数、平均步数、平均结果和标准偏差，请见表2～表5。

表1 单次迭代的平均时间对比Table 1 Average time comparison of each iteration

表2 函数f1 优化结果对比Table 2 Comparison of function f1 optimization results

表3 函数f2 优化结果对比Table 3 Comparison of function f2 optimization results

表4 函数f3 优化结果对比Table 4 Comparison of function f3 optimization results

表5 函数f4 优化结果对比Table 5 Comparison of function f4 optimization results

从表1 可以看出，单步迭代时间从长到短分别是QBICS、QBEA、BQGA、SCS。原因如下：（1）QBICS和QBEA 在每次迭代过程中，都需要对量子比特做投影测量、计算旋转矩阵和绕轴旋转操作，增加了算法的计算量。此外QBICS 和QBEA 几乎一致，原因在于：QBICS 增加的旋转幅角计算、种群退化程度这两个算子没有复杂操作，可忽略不计。QBICS 莱维飞行产生新解后的贪婪择优与QBEA 的任一个体随机旋转后的适应度计算的复杂度也是一致的。QBICS 仅是在交叉变异后，对变异个体需要重新投影测量，但数量少，并不耗时；（2）BQGA 与QBICS 相同，在Bloch 球面上也分别对应三个坐标，采用三链编码结构，但是染色体进化操作时不需要投影测量、绕轴旋转操作，更新过程相对简单，因此时间较短；（3）SCS是4 种算法中编码结构、个体更新最为简单的，染色体是单链结构，只有莱维飞行、Biased 随机扰动和贪婪择优，无需量子比特的Pauli 矩阵投影测量、绕轴旋转等复杂操作，因此单步迭代时间最短。

从表2 到表5 可以看出，算法的优化能力从高到低分别是QBICS、QBEA、BQGA、SCS。原因如下：

（1）QBICS、QBEA 和BQGA 三种算法都是Bloch 球面的三链结构，每条染色体一次进化都可以完成三个可行解的同时寻优，这无疑扩大了解空间的搜索遍历，获得问题最优解的概率得到提高，因此三种算法的收敛能力均高于SCS；

（2）QBICS 和QBEA 的进化效率高于BQGA，主要原因在于二者都是根据量子计算理论，通过绕轴旋转完成两个转角的协调更新和最佳匹配，向目标比特逼近时沿最短的Bloch 劣弧进行操作；

（3）比较QBICS 和QBEA：①绕轴旋转的幅角大小对于算法的进化速度和收敛至关重要。QBEA 采用的策略是δ∈［-0.05 π，0.05 π］的小距离随机旋转模式，QBICS 引入莱维飞行，在向目标比特逼近时，采用多次短距离探索和偶尔长距离行走的旋转模式，因此能够扩大搜索范围，更易跳出局部极值，因此收敛能力高于QBEA，可在更短的迭代步骤内完成收敛。②变异算子：QBICS 是利用Biased 随机走动和差分项对较差的个体进行变异，计算绕轴旋转角度时，除随机选择的个体外，还增加了与最优个体的夹角，并且根据贪婪策略进行择优，此策略可以在增加多样性的同时，在一定程度上增加了产生最优解的可能性，QBEA 仅为增加种群多样性使用Hadamard 门变异，变异后未进行贪婪择优，这势必可能会导致向种群引入更差的个体，个体前期的进化经验丢失，浪费一定的目标函数评价次数，此外，QBICS 变异概率是随种群进化程度动态调节的，对于保持种群多样性效果略优一些。③莱维飞行、Biased 偏好随机走动和贪婪择优实现了QBICS 的全局搜索和局部搜索之间的平衡，这一点是QBEA 所不具备的。此外，QBICS在搜索时减小了Bloch 球面搜索范围，引入Logistic混沌映射使得初始种群空间分布性较好，这两点也是QBICS 进化效率高于QBEA 的因素。

4 结论

量子计算与群智能算法的融合是目前的一个研究热点，受到国内外的关注。根据量子计算理论，提出一种量子行为衍生布谷鸟搜索算法。通过Bloch 球面描述的量子比特进行个体编码，表示当前鸟窝位置，通过投影、测量、绕轴旋转完成个体进化。QBICS提出采用莱维飞行确定量子比特的旋转角度，搜索范围限定到Bloch 半球以内，此外根据种群退化程度提出自适应的发现概率。结果表明，对现有的布谷鸟算法和量子行为进化算法的优化能力均有一定程度的提高。