基于反步滑模的无人车辆横向控制策略
郑雁南
(201620 上海市 上海工程技术大学 机械与汽车工程学院)
0 引言
通过数据挖掘道路交通事故案例,分析事故信息数据结构的现状和特点,道路状况差和驾驶员违反交通规则是引发事故的主要原因,尤其是超速、随意变道等[1]。据调查,驾驶员主观性失误所导致的交通事故占比有着逐年上升的趋势[2]。近年来,车辆智能辅助系统慢慢进入人们的视野,该系统包括感知、路径跟踪、决策等多个方面。在车辆的实际运行过程中,车辆通过毫米波雷达、定位导航等技术获取周围环境信息,所设计的控制器对已知环境信息进行路径规划并且进行轨迹跟踪[3]。通过建立车辆动力学模型,控制器通过制动和转向对横摆角速度和侧滑角进行控制,从而控制车辆完成对路径的跟踪,快速响应跟踪所规划的路径是评价控制器的好坏的重要标准。本文通过控制转向来完成对规划路径的横向控制研究。
本文的研究对象是四轮转向无人车辆。四轮转向极大提高了车身安全性和操纵稳定性,具有广阔的发展前景[4]。当前,该系统依靠轮胎横向力和转向角成正比,在轮胎横向力较小的情况下,为了更好地引入控制律,本文采用二自由度的运动学车辆模型。滑模控制器可以使得滑模面在较短时间内达到平衡点并趋于稳定[5]。反步控制器具备较高的灵活性来解决路径跟踪鲁棒控制的稳定性,比其他方法具有更低的局限性[6]。在控制器设计过程中,对于不确定常数系数,通过粒子群优化算法控制系统参数设计,优化滑动面和控制器输出,通过求解常系数最优解,将滑模控制器和反步控制器很好地结合起来。基于五次多项式曲线设计双排直车道模型以及变道路径规划,通过MATLAB/Simulink 与CarSim 的联合仿真,验证该控制器的稳定性,为测试在低时限下完成变道和低摩擦系数工况下的跟踪要求,设立3 s和5 s 变道时限,以及摩擦系数0.3 和0.9 四种工况,来证明所集成的反步滑模控制器针对极限工况有效。
1 路径规划
在路径规划中,通过动态约束以及初始五次多项式优化设计双排直车道模型,针对横向控制的仿真,开始与结束时间车子以直线移动,并且开始的横向速度和加速度为零,初始位置为零。
设五次多项式
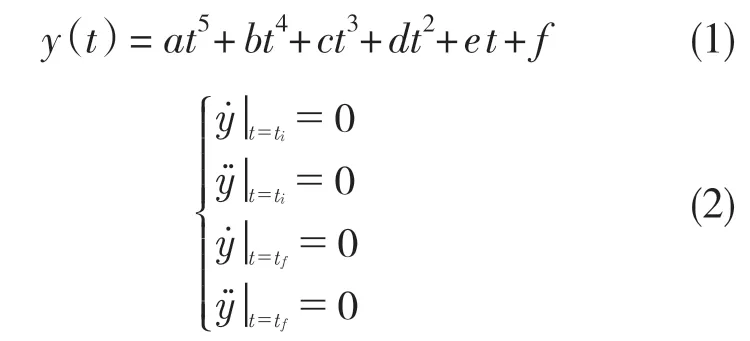
式中:a,b,c,d,f——五次多项式系数;ti,tf——操纵转向初始时间和完成换道时间节点。
两车道的中间间距

为了避免碰撞,利用卡尔曼滤波计算出换道的最小安全距离,即车道模型的中间间距w=3.75(w2-w1),设立3 s 变道时限(tf-ti)和5 s变道时限(tf-ti),得出2 个不同的参考路径,如图1 所示。
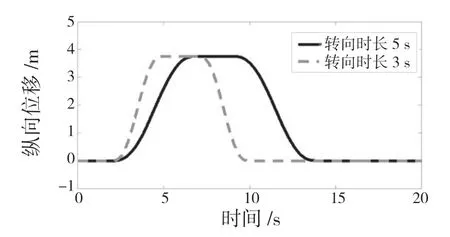
图1 双排直车道超车路径Fig.1 Overtaking path of two-row straight lane
2 车辆模型
2.1 车辆动力学模型建立
针对四轮转向无人车辆,研究横向控制的研究,可将复杂的车辆动力学系统简化为横向运动和侧向运动的二自由度模型,绘制出动力学模型并标注出横向位移、偏航率误差、前轮转角等参数。
图2 中:V——车辆过弯时行驶速度;β——车辆中心侧偏角;δf——汽车前轮转角;lf——车辆中心到前轴距离;e1——横向位移误差;e2——偏航率误差;lr——车辆中心到后轴距离。

图2 汽车动力学模型示意图Fig.2 Schematic diagram of vehicle dynamics model
由图2 汽车动力学模型可得出路径跟踪控制器状态空间表达式

式中:Cf——前轮侧偏刚度;Cr——后轮侧偏刚度;Vx——行驶速度;Iz——偏航惯性矩;ψ——偏航率。
依据状态空间表达设计控制器,车辆跟踪模型已经初步建立,但实际状况下,车辆跟踪过程中会产生误差,对于车辆状态变量的横向位移误差和偏航率误差,建立车辆跟踪误差模型的状态方程
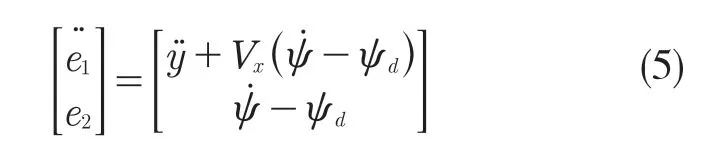
式中:ψd——期望的偏航率。
进一步求解,可得出考虑误差下的车辆的状态空间表达式

2.1 轮胎模型
采用“魔术公式”轮胎模型,设计了反步控制器,它是依据三角函数关系通过模拟轮胎数据得出的车辆动力学仿真分析,该模型的每一个参数都具有明确的物理意义并且具有仿真模型高度拟合的特点[7]。
3 控制器设计
3.1 反步控制器
在依据反步法设计控制器时,可将式(6)进行改进得出反步控制器的标准方程:
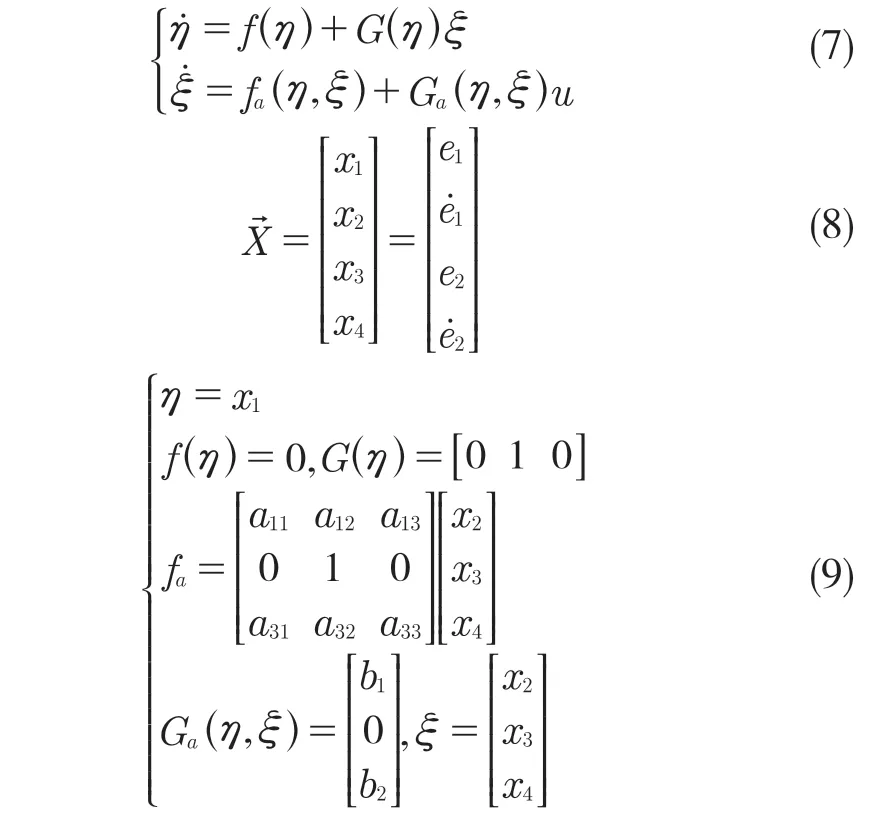
式中:μ——地面摩擦系数;ζ,η,u∈Rm;系数与表达式对照见表1。

表1 系数与表达式的对照表Tab.1 Comparison of coefficients and expressions
反步控制器具有强大的抗干扰,并且能够很好地处理不确定性参数。假设f,fa,G,Ga光滑的函数,并且f(0)=0,fa(0)=0,G,Ga为非奇异性矩阵。另外,假设系统公式(7)可使用反馈控制器控制其稳定性,令ζ=φ(η),φ(0)=0,列出关于η的李雅普诺夫函数不等式:

式中:V——李雅普诺夫函数。通过对其微分,得出满足其稳定性的理想输入,其中,控制律为
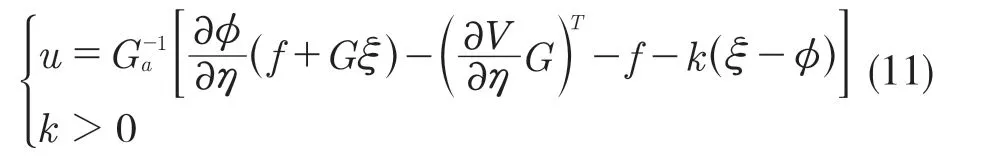
使用李雅普诺夫稳定性的证明方法,该控制律的稳定性:
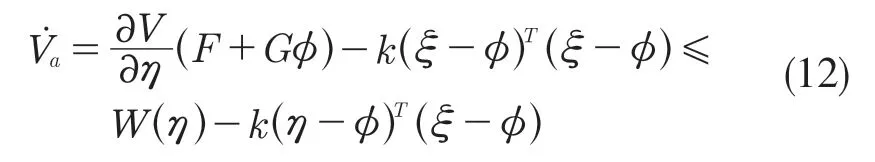
可得该方程在原点具有渐近稳定性,将上述反推控制器应用在汽车动力学模型上,则可以定义李雅普诺夫函数

将反步控制器控制规律应用在汽车动力学模型并简化
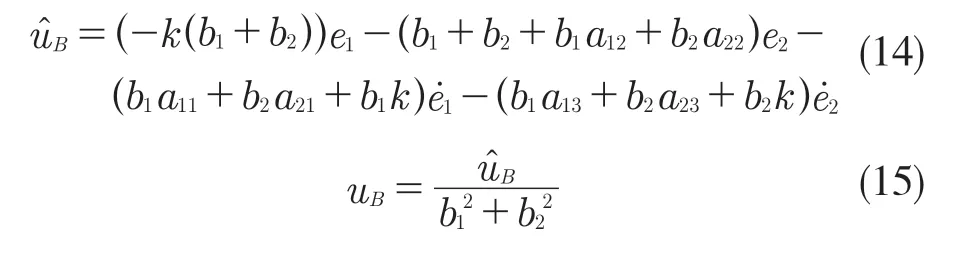
式中:uB——反步控制器的输入。
由式(14)可知,通过增大k 的值,可以降低不确定性参数对反步控制器产生的误差。
3.2 反步滑模控制器的设计
反步滑模控制器结构框架图如图3 所示。为了让控制器在更短的时间内达到平衡点,对反步控制器进行改进,在反步控制器的基础上集成滑模控制器。

图3 反步滑模控制器结构框架图Fig.3 Structure frame diagram of backstepping sliding mode controller
列出关于李雅普诺夫函数不等式

可以看出,当η=0 渐近稳定的平衡点,其滑动面S 为

则在η=0 这个平衡点李雅普诺夫候选函数为

结合式(7)对上述方程求导,满足其稳定性,得期望输入。其中控制律为
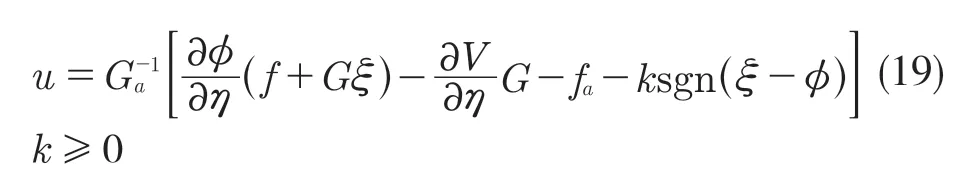
根据式(16)和式(19),使用李雅普诺夫稳定性定理证明所设计的反步滑模控制器的稳定性
因为k ≥0,对其求导可得

式中:σ——大于零的数。根据李雅普诺夫稳定定理,当外界扰动前,稳定性条件k 必须大于外界干扰,当k 不满足稳定性条件时,反步滑模器会选择更大的k,来消除干扰的影响,但是这也会造成控制输入的值变大。这里采用粒子群优化算法这种启发式优化算法来确定适当的成本函数,其通过迭代计算的方式改进可能的办法来解决问题。其原理是以最近符合条件的粒子数作为优化问题的候选解,通过设立最大迭代次数,不断迭代求出最优解,从而提高控制器的稳定性[8]。通过稳定性函数求微分,证明滑模面收敛于零:

通过使k 为正值,可证明滑模面收敛于零,为将其应用在车辆动力学模型上,可设立ζ=φ(η),并结合式(13)可得

在式(18)中,因为Ga矩阵得第2 行元素全为零,滑模面S2也为零,这对反步滑模控制器控制输入不会造成影响,由此可以得出反步滑模控制器的控制输入

式中:uBS——反步滑模控制器的控制输入,化简可得。

4 仿真结果与分析
本文对上述所提出的反步滑模控制器和反步控制器进行逐一仿真分析,通过MATLAB/Simulink 与CarSim 的联合仿真来实现。为了验证该控制器的稳定性,测试在低时限下完成变道和低摩擦系数工况下的跟踪要求。设立3 s 和5 s 变道时限以及低摩擦系数0.3 和高摩擦系数0.9 四种工况,描绘出两种控制器的运动轨迹以及规划的运动轨迹,反步滑模控制器滑模面S1和S2的变化,以及两种控制器的横向控制位移误差e1、偏航角误差e2、汽车转向角、偏航角、侧偏角和侧倾角随时间的变化关系曲线图。
图4 是所设计的两种控制器在高摩擦系数为0.9 和5 s 变道时长下的仿真结果,从横纵向位移图可以看出,在一般工况下,反步滑模控制器和反步控制器跟踪效果差别不大,都能很好地沿着五次多项式规划的超车路径进行。滑模面S1和S2是针对反步滑模控制器的绘制图,可以看见滑模面收敛于零,控制器输入不受到影响。在横向位移误差的处理上,反步滑模控制器明显优于反步控制器,偏航角误差、转向角、侧偏角和侧倾角两种控制器所反馈的变化曲线接近一致。

图4 在高摩擦和5 s 变道时长下的两种控制器对比Fig.4 Comparison of two controllers under high friction and 5-second lane changing
由图5 可知,在将高摩擦系数为0.9 改成低摩擦系数为0.3 时,在反步控制器控制的车辆在驶出原所在道路以及进入新的道路时,会稍稍偏离所规划的路径。而反步滑模控制器时能够完美地跟踪,并且可以看见滑模面收敛于零,控制器输入不受到影响。在横向位移误差和偏航角误差的处理上,反步滑模控制器都优于反步控制器,转向角、侧偏角和侧倾角反步滑模控制器所反馈的变化曲线振幅均小于反步控制器。
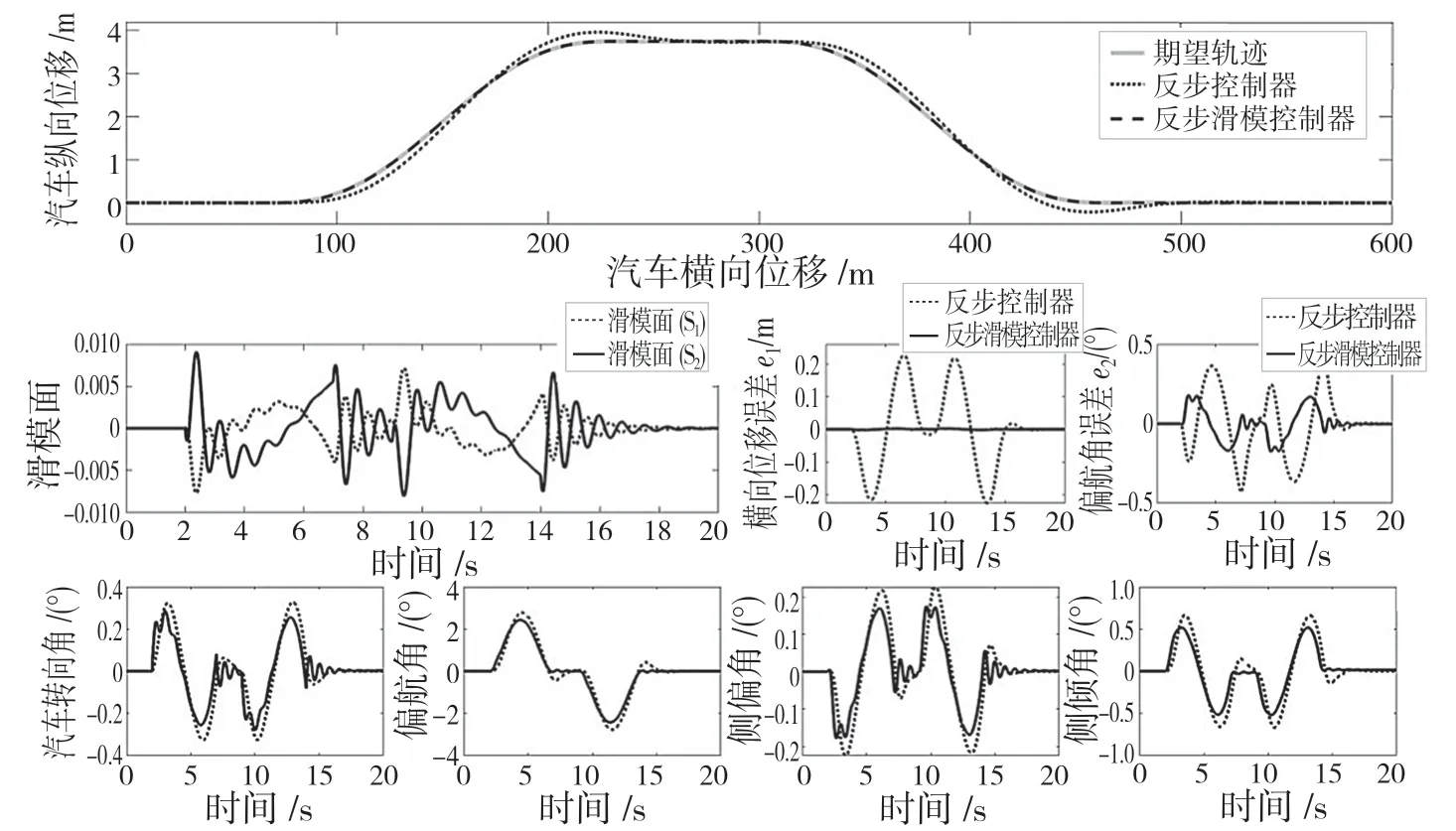
图5 在低摩擦和5 s 变道时长下的两种控制器对比Fig.5 Comparison of two controllers under low friction and 5-second lane changing
图6 是 在 图4 的 基础上缩短变道时长对2 种控制器的仿真结果。对比图6 和图4 可知,在高摩擦系数下,即便是缩短了变道时长,对两种控制器的稳定性并无影响。滑模面用更短的时长收敛于零,表现出了强鲁棒性。横向位移误差的处理上,反步滑模控制器依旧明显优于反步控制器,航角误差、转向角、侧偏角和侧倾角两种控制器所反馈的变化曲线接近,反应时长减小。

图6 在高摩擦和3 s 变道时长下的两种控制器对比Fig.6 Comparison of two controllers under high friction and 3-second lane changing
图7 是在低摩擦系数下减少为3 s 变道时长的仿真结果图,在低摩擦系数和极限变道时长下,反步滑模车辆控制器对轨迹跟踪十分稳定,而反步控制器所设计的车辆严重偏离期望路线,无法达到预计的跟踪效果,这是因为反步滑模控制器预先转向,能够用短的时间到达平衡点,这导致两种控制器的性能差别十分明显。除了转向角的变化频率、振幅都有所提升外,滑模面最后接近零,在横向位移误差、偏航角误差、侧偏角和侧倾角的处理上,反步滑模控制器明显优于反步控制器,这表明反步滑模控制器可以满足极限转向或湿滑工况的需要。

图7 在低摩擦和3 s 变道时长下的两种控制器对比Fig.7 Comparison of two controllers under low friction and 3-second lane changing time
4 结论
本文通过动态约束以及初始五次多项式优化设计双排直车道模型,建立二自由度的两轮车辆模型,并绘制汽车动力学模型。采用“魔术公式”轮胎模型,设计了反步控制器,并且反步法四轮转向无人车辆的路径跟踪算法进行改进,通过启发式优化算法结合滑模控制设计反步滑模控制器。即在反步滑模控制器设计过程中,对于影响控制器性能的常数参数,对于常数参数不确定的函数,通过粒子群优化算法寻找最优值,让反步控制器和滑模控制更好地集成。分别设立3 s 和5 s 变道时限以及摩擦系数0.3 和0.9 四种工况,通过CarSim 软件与MATLAB/Simulink 联合仿真,比较两种控制器横向偏移误差和偏航角误差曲线以及轨迹跟踪路线的贴合度,仿真证明在高摩擦系数下,即使是缩短转向时长,反步控制器和反步滑模控制器都能够很好地完成路径跟踪,但在低摩擦系数下,会使反步控制器稳定性降低,特别是在急速换道的工况下,然而,对于此类工况下所设计的反步滑模控制器能够很好地跟踪,证明所集成的反步滑模控制器针对极限工况有效。

