四轮移动机器人的模糊滑模轨迹跟踪控制

杨国东，刘泓滨，刘碧飞

（1.650093 云南省 昆明市 昆明理工大学机电工程学院；2.510030 广东省 广州市 三峡新能源珠江发电有限公司）

0 引言

四轮结构移动机器人是目前最常见的轮式机器人结构形式，四轮机器人的轨迹跟踪控制技术在监测、巡航、跟踪等领域应用广泛。本文研究的是四轮全向移动机器人，其轨迹跟踪（trajectory tracking）[1]控制方法是控制领域一大研究热点。轨迹跟踪控制是指机器人由控制器的作用从某一初始位置，跟踪一条关于时间的期望轨迹[2]。由于控制系统是一个多变量、强耦合、参数时变的多输入多输出非线性受控系统，且工作环境复杂，如何提高控制系统的抗干扰能力和实时性等，是当前研究面临的挑战[3]。

滑模控制是一种具有快速瞬态响应的鲁棒控制方案，具有建模简单、性能较好、鲁棒性较好等优点。但滑模控制系统有限的开关控制力及系统固有的运动惯性导致运动无法瞬时换向，又因系统以较快的速度到达切换线附近并来回穿梭，形成系统抖振[4]，从而影响系统性能。如今，消除抖振或未知参数影响的方法有自适应神经滑模控制[5]、自适应滑模控制[6]、模糊滑模控制[7]等。其中，模糊控制方法较简单，执行迅速，而模糊滑模控制结合了模糊理论和滑模控制各自特点[8]，能有效消弭系统抖振，提高系统的鲁棒性，运算简单，适用性强。文献[9]融合了速度控制器与滑模控制器，对未知函数进行模糊逻辑近似，并增加自适应模糊观测器的控制策略。但自适应控制系统存在潜在的大的超调和收敛缓慢等缓慢瞬态响应，且在滑膜中引入自适应机制难度较大，一定程度上限制了其工程应用[10]。文献[11]使用滑模的思想设计控制器，提出了一种带有模糊快速双幂次趋近律的全局渐进稳定滑模控制方法，但其研究对象不属于全向移动机器人。

本文基于可全向移动四轮机器人运动学方程，首先设计了积分滑模控制器。进而为了提升轨迹跟踪效果，结合模糊与滑模两种方法的优点，设计模糊滑模控制器，用Lyapunov 函数证明其稳定性。运用模糊滑模变结构的控制计策，设计一对模糊控制器对采用积分策略估计的切换控制参数进行调整。最后，通过仿真验证其有效性。该方法跟踪精度好，减缓抖振效果明显，轨迹跟踪品质更优秀。

1 建立四轮机器人运动学模型

本文以4 个45°麦克纳姆轮对称分布的四轮移动机器人作为研究对象，每个驱动轮采用独立的电机驱动。建立平面绝对坐标系XOY，跟踪坐标系XtOtYt，Ot位于移动机器人的几何中心，如图1 所示。

图1 四轮移动机器人位姿误差Fig.1 Pose error of four-wheel mobile robot

则四轮机器人的运动学公式为

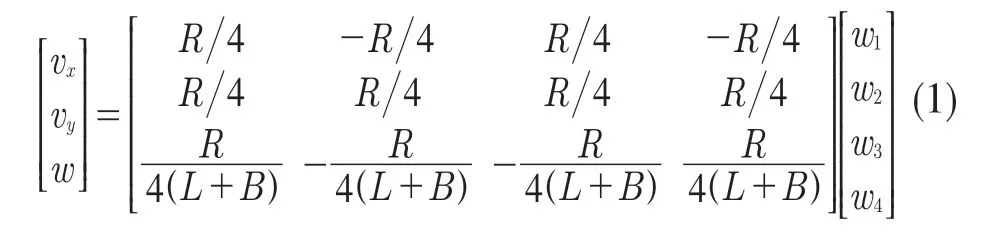
式中：R——轮子半径；wi（i=1，2，…，4）——各轮子的角速度；L，B——轮子轮心到坐标系XtOtYt纵轴和横轴的间距；vx，vy——机器人的X轴，Y 轴的平移速率；w——机器人旋转的转速；θ——机器人与XOY 坐标系X 轴的夹角。各轮之间的速度约束关系w1+w3=w2+w4，vx=vtcosθ，vy=vtsinθ，vt——线速度。

因四轮机器人工作环境多为平整地面，忽略运动过程中的轮子打滑、抱死等现象的影响。机器人逆运动学公式为

假定绝对坐标系的初始位姿为C=[x，y，θ]T，期望位姿G=[xg，yg，θg]T，四轮机器人从XtOtYt到XOY 坐标系的位姿换矩阵为

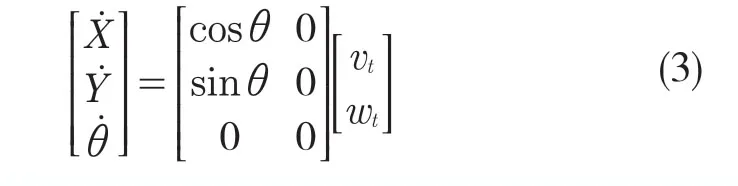
四轮机器人线速度与角速度在绝对坐标系下的映射关系为[12]

式（4）拆解后微分得到

式中：θe——航向角误差；xe，ye——xt，yt轴向误差；wt——机器人转动的角速度；vg——速度指令；wg——角速度指令。

2 四轮机器人控制器设计

2.1 滑模控制器设计

滑模控制过程可描述为，从空间任意一点出发的状态轨迹能在特定时间内到达滑模面，并在其上发生滑动模态运动，最终达到平衡点的控制过程。设计图2 所示积分滑模控制器。假定四轮机器人的参考位姿Pc=[xg，yg，θg]T、速率qc=[vg，wg]T；系统输出为当前速率qt=[vt，wt]T。滑模控制器依据位姿偏差pe=[xe，ye，θe]T和参考速度qc获得当前控制速度qt和当前位姿pt=[xt，yt，θt]T，通过系统控制使跟踪位姿误差pe→0。

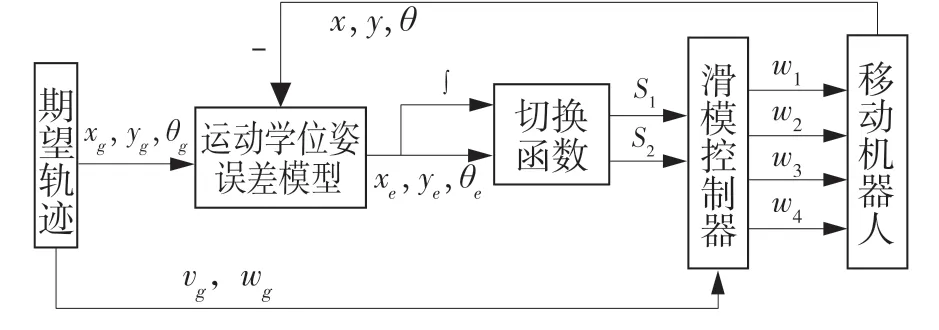
图2 积分滑模控制结构图Fig.2 Integral sliding mode control structure diagram

根据式（5）转化为状态方程为

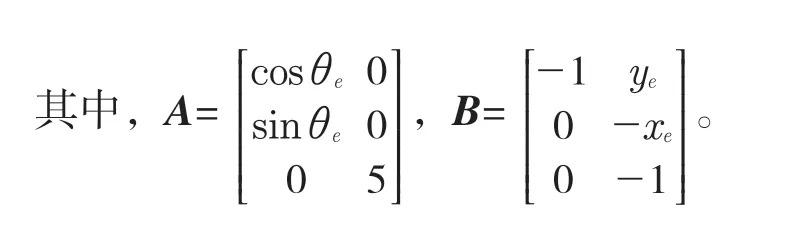
由于四轮机器人控制系统为多输入多输出系统，为加快趋近速率，设计基于sigmoid 饱和函数的滑模切换函数[13-15]

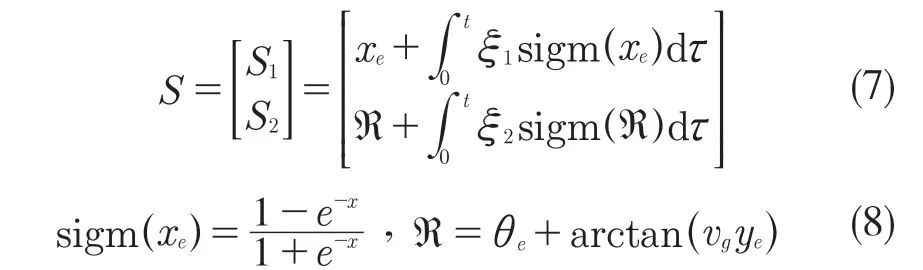
式中：ξ1，ξ2——正值常数。

联立式（7）和式（8）求导可得

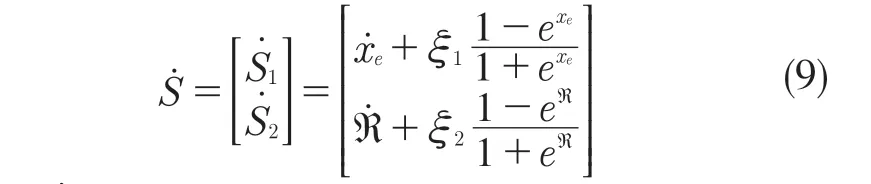
本文用连续函数来取代符号函数的切换控制削弱抖振和外界扰动的影响，即

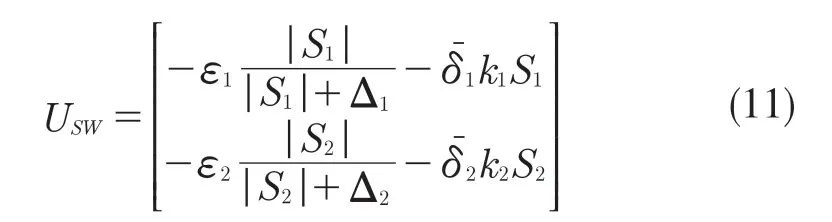
式中：k1，k2，ε1，ε2——大于0 的数；δ1，δ2——大于0 的极小值；Δ1，Δ2——趋于零的正小数。

得到积分滑模轨迹跟踪控制律为

证明切换函数S2的稳定性，切换函数S1的证明相似。定义Lyapunov 函数为

2.2 模糊滑模控制器设计

为了达到更好的轨迹跟踪效果，本文采用饱和函数来减弱系统抖振，通过模糊算法对饱和函数的参数进行调节。在积分滑模控制器的基础上，设计2 个模糊控制器分别对进行调节以减弱抖振。当系统状态点与滑模面的间距很远时，加大控制力度；反之，则削弱控制力度，抑制抖振。控制系统结构如图3 所示。

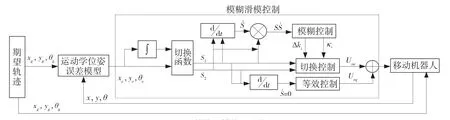
图3 模糊滑模控制结构图Fig.3 Structure diagram of fuzzy sliding mode control

可将式（12）的滑模控制律调整为

当切换函数S 的值很小时值也很小，此时为了保证品质，须把ki值增大来减弱抖振；反之，当切换函数S 值很大时，增大值，减少ki值，以此将趋近速度提高，同时又可以防止较大的控制动作。

选择论域为[-1，1]的S11模糊控制器1 作为输入，选取切换控制中论域分别为[-0.1，0.1]和[-2，2]的参数，Δk1为控制输出[16]，系统的输入输出模糊集合定义如下：

式中：NB，NM，NS，NL，ZO——“负大”“负较大”“负中”“负小”“零”；PL，PS，PM，PB——“正小”“正中”“正较大”“正大”。

表1 和Δk1 的模糊规则Tab.1 Fuzzy rules ofand Δk1

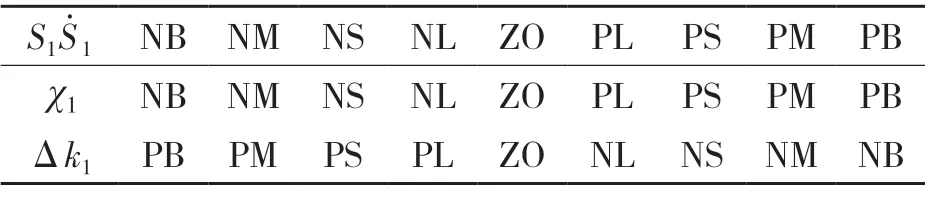
表1 和Δk1 的模糊规则Tab.1 Fuzzy rules ofand Δk1

采取“重心法”进行反模糊化得到输出值

由式（15）～式（17）、式（20）可以得到模糊切换控制为

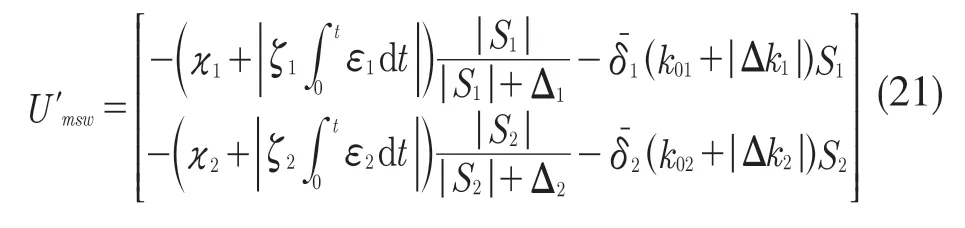
将式（21）代入式（18）得到模糊滑模控制律，见式（22）：

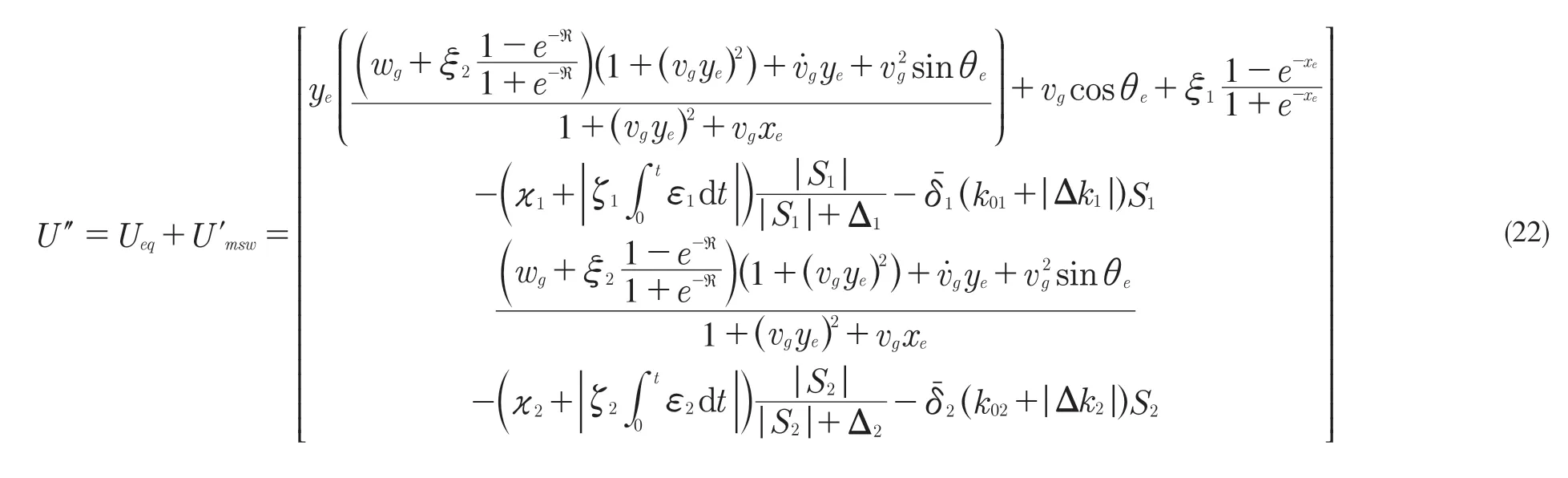
3 仿真分析验证

在MATLAB 上进行仿真试验。选取具有代表意义的直线和圆形参考轨迹进行仿真分析。选取初始速度为2.5 m/s，仿真时间为20 s，将模糊滑模控制（FSMC）与积分滑模控制（SMC）进行轨迹跟踪仿真对比。选取L=0.75 m，B=0.7 m，R=0.072 m，各项仿真参数：Δ1=Δ2=0.1，ζ1=ζ2=0.2，ε1=ε2=0.01，k01=4，k02=2，ξ1=ξ2=2，δ1=δ2=0.01。

3.1 直线轨迹

进行直线轨迹跟踪验证，假定期望轨迹起始位姿为[1，0，π/3]T，实际跟踪起始位姿是[0.5，0，π/3]T。根据图4—图6 结合表2 数据可知，实际跟踪轨迹能较快与期望轨迹重合并保持稳定运行，模糊滑模（FSMC）控制误差收缩更快控制精度更好。图6 可验证四轮移动机器人直线运动时，角速度恒定且w1=w3，w2=w4。

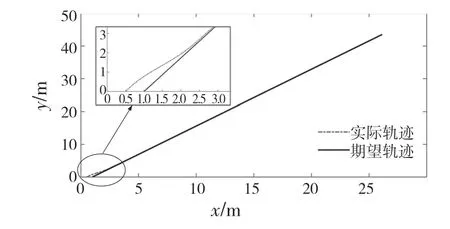
图4 FSMC 直线轨迹跟踪结果Fig.4 FSMC linear trajectory tracking results

图5 FSMC 与SMC 直线轨迹跟踪误差Fig.5 FSMC and SMC linear trajectory tracking error

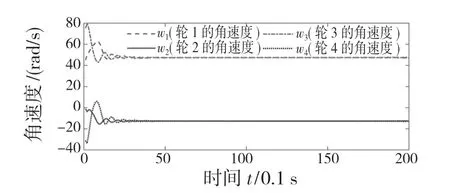
图6 FSMC 直线轨迹跟踪各轮角速度Fig.6 FSMC linear trajectory tracking angular velocity of each wheel

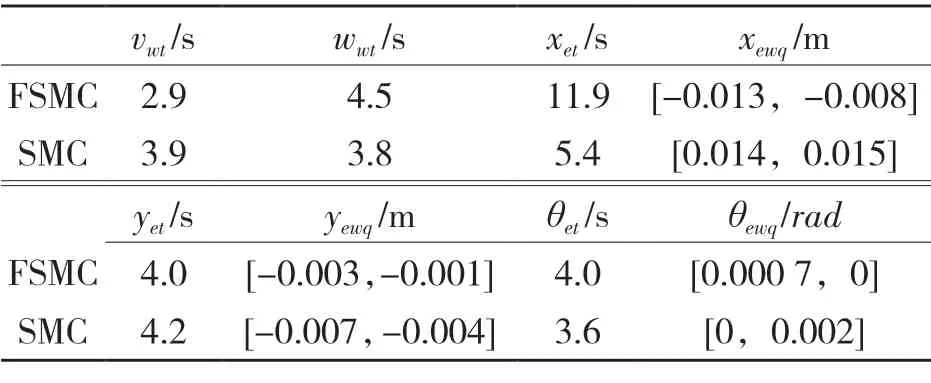
表2 FSMC 与SMC 直线轨迹跟踪仿真结果对比Tab.2 Comparison of FSMC and SMC linear trajectory tracking simulation results

表2 及表3 中：vwt——线速度达到稳定的时刻；wwt——角速度达到稳定的时刻；xet，yet，θet——横向和纵向误差以及航向角误差达到xewq，yewq，θewq横向和纵向误差区间以及航向角误差趋于稳定的误差区间的时间。

3.2 圆形轨迹

以半径为4 m 的圆进行仿真验证。任意设定起始位姿为[2，0，0]T。根据图7—图9 和表3数据可知，机器人能够较好地跟踪圆形曲线，过程稳定运行。模糊滑膜（FSMC）控制的轨迹跟踪算法较好地消除系统抖振，机器人速度波动更小，稳定更快，且跟踪精度更高。

图7 FSMC 圆形轨迹跟踪结果Fig.7 FSMC circular trajectory tracking results

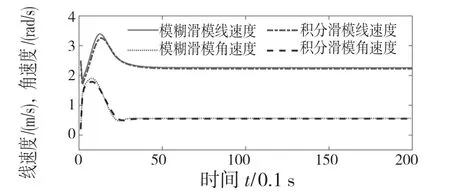
图8 FSMC 圆形轨迹跟踪线速度与角速度对比Fig.8 Comparison of linear velocity and angular velocity of FSMC circular trajectory tracking

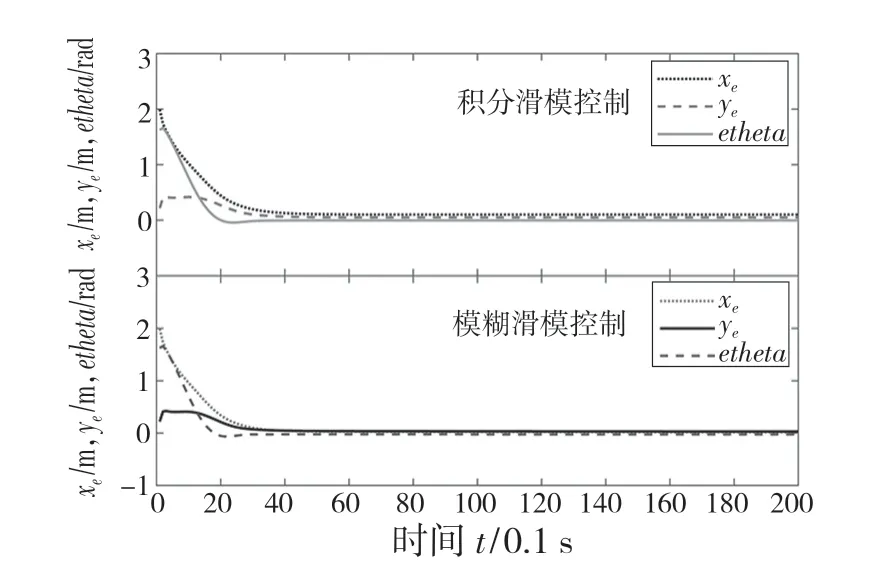
图9 FSMC 圆形轨迹跟踪误差对比Fig.9 FSMC comparison of circular trajectory tracking errors

表3 FSMC 与SMC 圆轨迹跟踪的仿真结果对比Tab.3 Comparison of simulation results of FSMC and SMC circular trajectory tracking

4 结论

本文研究四轮移动机器人的轨迹跟踪控制方法，对普通滑模控制方法进行改进，以四轮机器人的运动模型为基础设计了一种易于实现的模糊滑模轨迹跟踪控制方法。采用模糊控制对滑膜控制器中切换控制的相关参数i，Δki（i=1，2）进行估计和调整，通过MATLAB 编程分别对直线轨迹与圆形轨迹仿真验证，结果表明，本文模糊滑模控制器能抑制滑模控制产生的抖振，有更好的轨迹跟踪品质，兼具模糊控制与滑模控制的优势。