77 GHz 近程雷达CFAR 算法研究*

杨 威，崔恒荣

（东华大学，上海 201620）

0 引言

近程探测雷达的应用已经深入到军事、民用和汽车等领域的各个方面，如机场跑道异物（Foreign Object Debris，FOD）[1]检测和汽车防撞雷达[2-3]。相比于传统的激光、超声波和摄像头等技术，毫米波雷达系统在复杂天气适应性、分辨率和作用距离上有了很大的突破。近程雷达的自动检测主要依靠雷达技术和图像识别技术来实现，由于所处环境杂波复杂且相对目标较强，因此需要使用恒虚警（Constant False Alarm Rate，CFAR）检测技术来保证有效的检测性能。毫米波雷达检测系统主要采用毫米波调频连续波（Frequency Modulate Continuous Wave，FMCW）雷达，主要利用了其高距离分辨率和高精度的优点。本文主要涉及近程雷达静态FOD 检测。

CFAR 算法中最具代表性的是单元平均恒虚警检测（Cell-Average CFAR，CA-CFAR），是利用待检测单元的相邻单元来估计背景杂波的功率并计算出检测门限值[4]。现有很多CFAR 检测算法的研究都是通过仿真来实现[5-8]，但通过实测数据进行的研究较少。文献[7]使用MATLAB 仿真来改进CA-CFAR 算法，并通过尖峰值来处理杂波边缘实现在非均匀环境下的多目标检测。文献[9]从仿真和实测的角度研究了外辐射源雷达的CFAR 检测算法，将实际操作过程中的各种客观因素与仿真相结合来分析。然而，实际工程应用中，并不能直接对得到的雷达的回波信号进行CFAR 检测分析。具体地，对于本文使用的FMCW 雷达而言，需要对本振泄漏进行预处理。

本文通过对测得的回波信号进行相参积累来消除噪声，并利用对消技术消除泄露信号还原出目标信号。通过分析得出泄露信号消除后存在的频谱泄漏的情况会导致目标单元的旁瓣较宽，因此CACFAR 检测算法的保护单元的选取就显得至关重要。传统的算法保护单元选择数目固定不变，不能适应实际情况，因此提出了自适应保护单元数的单元平均恒虚警（Protect Cell Average-CFAR，PCACFAR）检测算法。该算法对信杂比较大且所处单元旁瓣较宽的目标能完成较好的检测。

1 FMCW 雷达基本原理

调频连续波雷达根据调制波形的不同可以分为锯齿波调频、三角波调频和正弦波调频等[10]。FMCW 雷达在扫频周期上发射频率连续变换的连续信号，当接触到物体反射回来后，接收信号和发射信号会产生一个频率差（差频），根据这个差频信号可以间接测算出时间，进而解算出目标距离和速度信息。图1 为锯齿波调频雷达的工作原理。

图1 FMCW 雷达系统锯齿波工作原理

图中：f0为初始频率；B为调频带宽；Tm为调频周期；fb为差频；τ为发射与接收信号的时延。可以看出，FMCW 雷达发射信号和接收信号波形相同，仅在时间轴上延长了时间τ。在任意时刻，雷达发射信号ST(t)可表示为：

式中：At为发射信号幅度；f为发射信号频率；φ0为发射信号初始相位。对于FOD 来说一般是静止目标，假设目标在距雷达R0的位置，则发射信号和接收信号之间存在一个回波时延τ=2R0/c。根据图1，以第一个调频周期为例，不考虑初始相位，假设对任意的时刻t(0 ≤t≤Tm)，发射信号的频率可表示为：

式中：μ=B/Tm表示调频斜率，根据频率可求出发射信号的相位：

于是，同样在t0时刻，接收信号与发射信号混频，可得差拍信号：

根据频率与相位的关系，可以得到差频为：

可以得到静止目标的距离R0与差频fb的关系为：

本文针对的场景是静态FOD 检测，故直接通过对锯齿波调频雷达的差拍信号做处理得到精确的FOD目标距离信息。FOD 检测雷达的相关参数如表1 所示。

表1 雷达主要参数

2 相参积累

雷达的回波信号中噪声强度一般远大于目标信号强度，但是噪声分量具有随机分布的特性，通过相参积累的方法可以有效地提高信噪比，同时也能提高CFAR 检测性能。在FMCW 雷达中，雷达内部直接数字频率合成（Direct Digital Synthesis，DDS）扫频源等频率源生成的信号在每段扫频周期内的相位变化是相同的，且脉冲之间的相位是相对固定的。若将N个扫频周期的雷达回波信号进行相参积累，理论上信噪比可以提高到N倍。但是在实际应用中，考虑到信号处理的实时性，N的值也不能选取得太大。运动的目标会因为存在多普勒频移，一般需要通过快速傅里叶变换（Fast Fourier Transform，FFT）对每项移相相加。对于静止目标如FOD 来说，根据第1 节对FMCW 雷达的信号分析可知，差拍信号在扫频周期上的相位变化相同，直接将这N个周期相加求平均值即可。

假设采集得到N段信号，记为V1(t),V2(t),…,VN(t)，噪声信号用Ni(t)表示，除噪声以外的目标FOD 信号、杂波以及泄露信号用S(t)表示，则相参积累后的信号为：

通过相参积累后，噪声分量的幅值下降到了原来的1/N，而目标信号的幅度会保持不变，有效地提高了信噪比。本文通过采集FMCW 雷达多段扫频周期上的输出信号用来做相参积累，实现更佳的检测性能。检测的对象是相对雷达静止的目标，如图2 所示，为测试20 m 处的FOD 时采集的12 个周期的雷达回波信号。

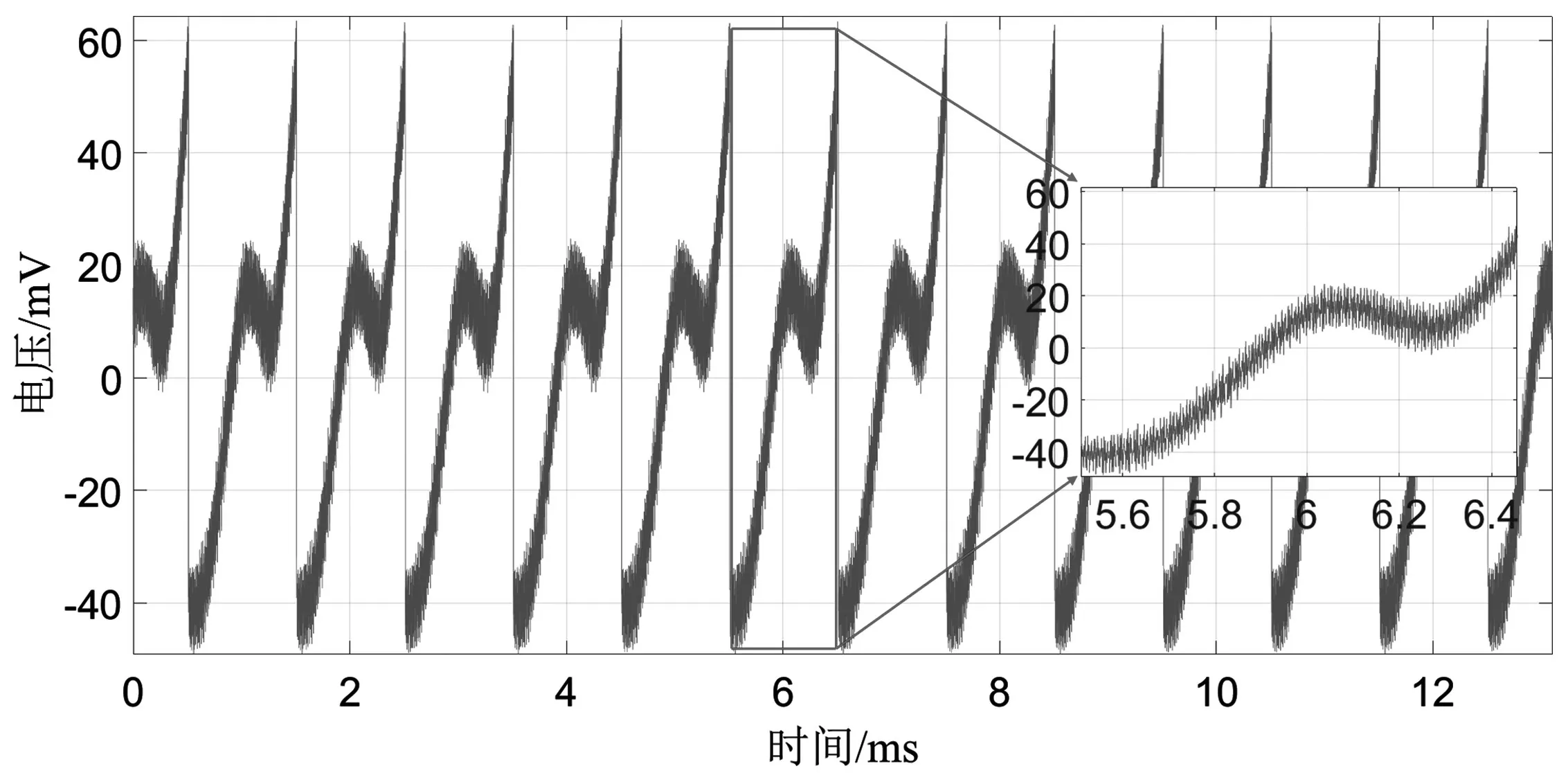
图2 实测雷达输出数据

3 频谱泄露

相参积累在一定程度上削弱了噪声，提高了信噪比，但还需要对泄露信号进行消除。实验使用的是锯齿波调频雷达，从图3 可以看出，雷达输出信号明显存在本振泄露的问题。本振泄漏是指零中频架构的接收机混频器的射频信号端和本振端的隔离度不够，接收链路中出现与射频信号同频的本振信号[11]。

图3 原始泄露信号时域波形

本文使用了对消技术[11]来处理泄漏信号，图2为不包含任何目标信号的纯净泄露信号，将此纯净信号反相180°后与测得的目标信号相加之后得到带有目标差拍信号、杂波以及少量噪声的信号。在实际工程中，要想做到完美地消除基本上是不可能的，总会有残留的泄漏信号，因此雷达输出信号的中心幅度与对应的纯净泄露信号不可避免的存在一些偏差。由于信号输出存在误差，二者做相消处理后，信号波形的某部分会相对水平轴发生偏移如图4 所示。

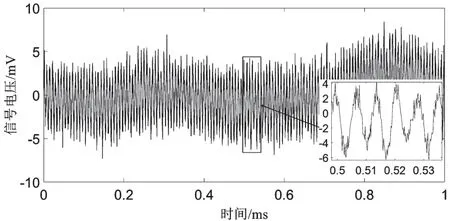
图4 消除泄露信号后的时域波形

从图4 可以看出，通过相参积累还原后的信号不是一个完整周期，信号的起点和终点值也不同。这是因为进行FFT 处理时会对此有限长度的信号进行周期延拓，周期延拓产生的信号在连接点处会存在突变的情况，因此还原出的无限长信号不能完整的代表原始差拍信号。由于这时得到的FFT 频谱不只是单条谱线，因此会在目标信号频率处出现会产生频谱泄漏，频谱产生拖尾而变宽。此外，目标基频幅值越大，谐波成分的幅度也越大，二者有一定的正比关系。相应地，在目标频率处频谱越宽，能量泄露到相邻单元越多。由于FMCW 雷达测距通过差频来求，在测静止的FOD 目标时，差频与距离是相对应的，则通过对相参积累后的回波信号进行频域变换就可以得到相应的距离单元图。下一步进行CFAR 处理，针对不同幅度下频谱展宽的情况提出PCA-CFAR 算法。

4 PCA-CFAR 算法

本文测试的道路环境相对均匀，目标特征相对明显。杂波主要来自道路上许多小的散射体的回波，杂波的幅度大致服从瑞利分布，而CFAR 检测算法的理论推导大部分是基于瑞利分布模型进行的，所以选取瑞利模型下的检测算法。

传统的CFAR 检测方法有CA-CFAR、单元平均取小CFAR（Smallest Of-CFAR，SO-CFAR）和单元平均取大CFAR（Greatest Of-CFAR，GO-CFAR）等[4]。由于实测的杂波数据服从瑞利分布且测试环境比较均匀，本文在CA-CFAR 的基础上进行改进。

由第3 节对频谱泄露的分析可知，在实际工程中，功率泄漏的情况很明显，这时CFAR 算法中保护单元的选取会很大程度上影响检测结果。一方面，如果保护单元太少，杂波功率估计值会偏大，导致检测门限变高，因此很容易出现漏警；另一方面，保护单元也不宜取得太多，会影响算法的时间复杂度，还会恶化多目标检测性能。由于目标单元幅度越大，旁瓣越宽，且幅度衰减较为平滑，因此本文选择根据目标单元的信杂比来确定保护单元的数目，PCA-CFAR 算法的原理图如图5 所示。

图5 PCA-CFAR 原理

图中：D 为待检测单元，其信杂比为d-c，其中c为杂波功率；P 为保护单元。保护单元的功率不参与杂波功率的估计，防止待测单元能量泄漏导致检测门限过高而发生漏警。保护单元数目通过待检测单元的信杂比和阈值因子β来确定，称为保护阈值。保护单元选择阈值为：

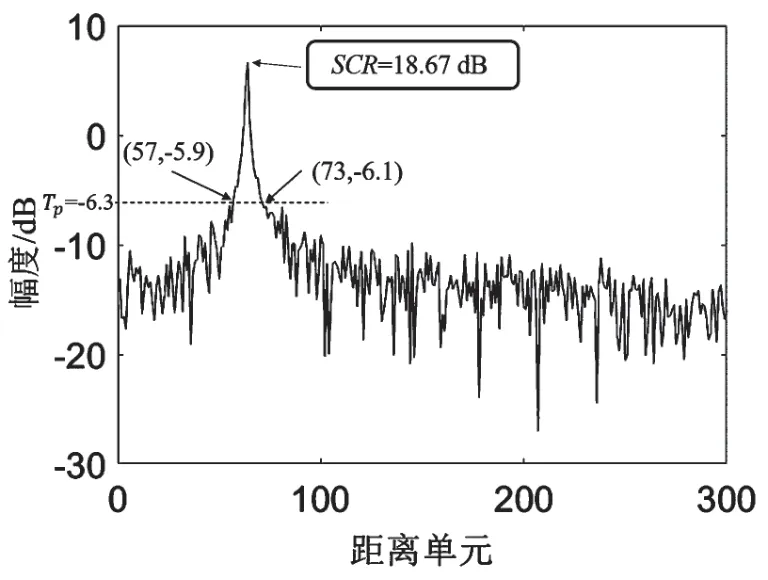
图6 保护阈值

按图5 的流程计算检测门限T=Y×α，将检测门限值与检测单元值进行比较来判断目标存在与否。具体判决公式如下：

如式（11）所示，若检测单元的幅度大于检测门限，则假设H1成立，判决为存在目标；反之假设H0成立，检测单元不存在目标。

5 实验验证及结果分析

5.1 实验环境

由于条件限制，本文无法在实际机场跑道进行实验。为了尽可能模拟机场跑道的测试场景，本文在室外的道路上进行了实验以验证PCA-CFAR 算法的检测效果，实验环境如图7 所示。

图7 实验测试环境

其中稳压电源给雷达上电，高速AD 采集卡为EVAL-AD7960FMCZ，其采集雷达输出信号经USB 传输到PC 端，PC 端将上传的雷达信号数据保存到本地以供处理。由于距离越远回波信号越弱，测得的目标信杂比也越小，本文对不同距离上的FOD 进行检测，测试距离范围为10～60 m，每隔10 m 做一次测试，共6 组数据。表2 列出了测量得到的不同信杂比情况下计算得到的保护单元数目。表中信杂比是根据单独测得的杂波功率确定的。

表2 目标距离单元、信杂比测量结果

5.2 目标检测

PCA-CFAR 算法检测的相关参数为：虚警概率Pf=10-6；参考单元数目为N=20；门限因子α=N(Pf-1/N-1)=15.57；杂波功率Pc=-12 dB。下面对表2 的实测数据进行进一步的检测分析。

图8 为雷达回波信号和检测门限的比较，目标位于第64 个距离单元，图8 中，下方黑色细线为含有目标的回波信号，上方黑色实线和虚线分别对应自适应调整保护单元数目Np为16和4时的检测门限。

图8 不同保护单元数目的大信杂比目标检测

从图8 可以看出在信杂比较大的情况下，通过自适应优化保护单元数目后目标可以很好地检测到，而如果保护单元太少则会发生漏检。这是由于保护单元太少时，高功率的旁瓣落入了参考单元内，背景杂波的估计功率值提高，导致检测门限过高发生漏检。

图9 为图8 选择不同保护单元数目时的检测概率曲线图。可以看出，随着保护单元数目的增多，检测概率也随之提高。相比于传统CFAR 算法的固定4 个保护单元数目，保护单元数为16 时检测概率提高了71%，但是增大到一定程度即Np大于16后，检测概率增加得比较平缓，且此时泄漏的功率基本上都落在保护单元内。由于Np太大则会增大CFAR 损失，因此，Np取16 是最合理的。

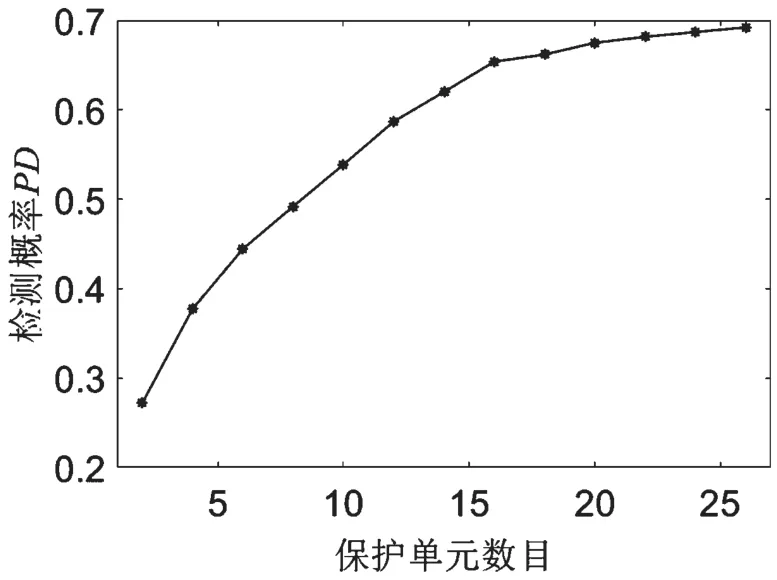
图9 不同保护单元数目的检测性能

图10 为信杂比较小的目标检测结果。图10（a）为处在第166个距离单元，信杂比为14.01 dB的目标，取保护单元数目为6 后可以正常检测到。图10（b）为更远的第199 个距离单元，信杂比为12.40 dB 的目标，取保护单元数为4 时仍能检测。对于远距离的目标，信杂比小且旁瓣较窄，通过自适应的调整保护单元的数目后也可以检测到。相对于前面大信杂比的情况，一方面能使检测的距离分辨率提高，另一方面还能有效地减少数据冗余。

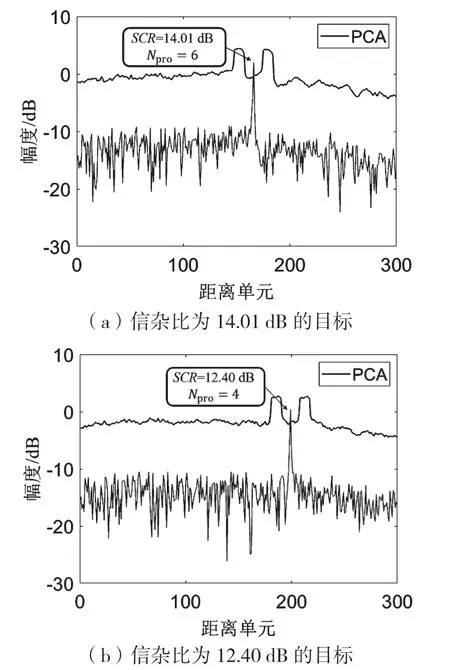
图10 小信杂比的检测结果

5.3 性能分析

设虚警概率Pf=10-6，参考单元数目N=20。图11展示了保护单元个数分别为4、10、16 时PCA-CFAR 算法的检测性能。

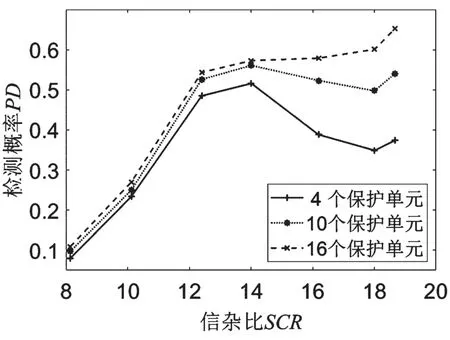
图11 PCA-CFAR 算法的检测性能

可以看出，当信杂比较小时，保护单元的选择对检测概率的影响较小。这是由于信杂比较小时，功率泄露的情况不明显，只对相邻少数几个单元影响较大，较远的淹没在杂波之中，即使保护单元取很多杂波功率估计值相差也不大，检测概率也基本相同。但是随着信杂比的增大，功率泄露情况更加明显，保护单元的选择对检测概率的影响则越来越大，而太少会使得检测概率急剧恶化，甚至会比小信杂比的检测概率低。因此，通过PCA-CFAR 算法自适应确定保护单元数可以有效地提高检测性能。

6 结语

本文讨论了近程雷达在实际应用中的目标检测问题，介绍了所使用的调频连续波雷达的工作原理。针对实测回波信号进行相参积累和泄露信号消除后存在频谱泄漏的情况，提出PCA-CFAR 算法。本文算法通过信杂比确定保护单元的选择阈值，目标单元左右高于阈值的单元被纳入保护单元中，使得背景杂波的估计值和理论值更接近，从而得到更优的检测结果。分析测试结果可知，自适应保护单元数的PCA-CFAR 算法可以稳定的检测到信杂比较大且频谱旁瓣较宽的目标，并且能获得较高的检测性能，对信杂比较小的目标也能完成有效检测，对于今后CFAR 算法的工程实现有很大的借鉴意义。