一种时变交互多模型融合目标跟踪方法

栾铸徵，俞成龙，顾 兵，赵先涛

(中国船舶重工集团公司第723 研究所，江苏 扬州 225101)

0 引言

因为目标受航路、动力及环境等因素影响，目标总是在做机动运动，例如反舰导弹末端变轨，高空制导炸弹抛物线运动时受到空气阻力和重力的作用，旋翼无人机受人为控制飞飞停停等。这种机动性往往是不可预测的，使用单一固定的滤波模型很难准确跟踪机动目标状态，滤波器结果会发散，导致跟踪失败。因此由Blom 和Bar-Shalom 提出交互多模型(IMM)算法，采用基于位置、匀速、匀加速、Singer 等多种滤波并存方式，目标状态估计是多个滤波器交互作用的结果，采用马尔可夫(Markov)链控制模型间的交互，把各个模型上一时刻的滤波值进行交互作用作为各模型的下一时刻的输入，然后分别进行滤波，得到的结果进行模型概率加权输出作为最终的结果，效果比单模型的好，从而IMM 算法广泛应用到各个领域[1-4]。但在常规IMM中马尔可夫转移概率矩阵是固定值，并且模型概率是通过卡尔曼滤波(Kalman)更新过程中产生的残差来更新模型概率，模型概率更新及模型概率转移没有结合当前的目标状态分布。所以本文提出了以模型间似然函数(Likelihood Function)及多模型贝叶斯后验估计(Bayesian Estimation)融合思想，采用当前模型跟踪结果更新模型交互概率和以贝叶斯估计融合多模型输出作为目标状态更新值，与目标实际机动情况更加符合，本文对强机动目标和扰动静态目标进行了基于Kalman 滤波器的时变IMM 模型融合算法(TV-IMM)和常规IMM 方法(C-IMM)仿真，结果表明时变IMM 模型融合算法比常规IMM 方法更有效。

1 时变交互多模型融合理论分析

本方法仍然采用IMM 处理架构，时变交互多模型融合滤波算法原理是同时使用多种滤波器对应多个运动模型，基于贝叶斯后验估计的方法得到目标当前状态的最小均方差估计。首先根据模型概率和模型交互马尔可夫转移概率完成各个模型之间的输入交互作用，结果输入给各个滤波器预测和更新状态，用各个滤波器目标状态分布求解模型间马尔可夫转移概率，同时输入给多模型融合器，根据贝叶斯后验概率估计原理得到目标状态分布更新，再根据似然函数原理更新模型概率，从而完成多模型滤波的闭环跟踪。

与常规IMM 不同点在于马尔可夫转移概率矩阵计算方法、目标状态分布更新算法、模型概率更新算法上有不同。该滤波器实现流程如图1 所示，假设有r 个卡尔曼滤波器模型同时用于目标跟踪，模型间满足相互独立的多维高斯分布特性。TV-IMM 算法可总结为如下5步：模型输入相互作用、模型滤波输出、模型输出融合、模型概率更新、模型间转移概率更新。

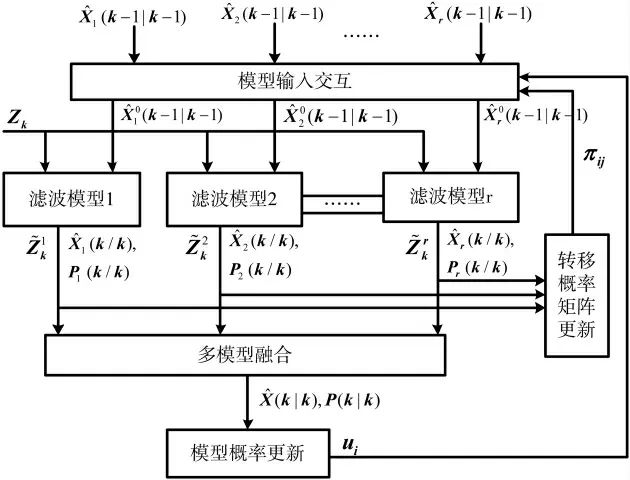
图1 时变交互多模型融合滤波器结构

1.1 模型输入交互作用[1-5]

该过程和IMM 交互多模型一致，就是把各滤波器初始条件混合。利用上一步k-1 时刻得到的模型概率μj(k-1)和马尔可夫(Markov)交互概率矩阵交互作用，产生新的模型交互概率，代表了模型间相互影响的程度。交互概率作用在每一个模型的滤波结果(k-1|k-1)，Pj(k-1|k-1)，其中j=1，…，r，得到输入交互，马尔可夫转移矩阵πij表示：

Markov 矩阵第i 行表示第i 个模型转换为其他模型的概率。第j 列表示由其他模型转换到第j 个模型的概率。由于各个模型对目标跟踪影响程度不同，用模型概率ui表示模型i的影响程度，则第i 个模型转化为第j 个模型的概率修正为：

可见模型概率ui影响模型交互概率uij(0)，模型间转化概率满足概率空间完备性，即第j 列概率总和为1：

概率空间由修正概率组成，所以模型交互概率由归一化为：

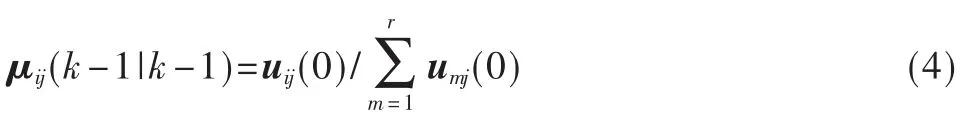
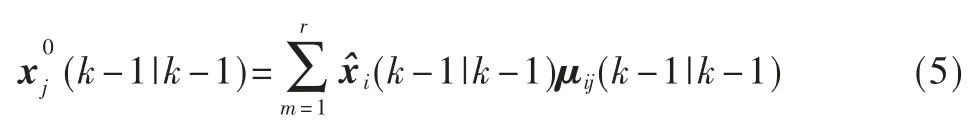
第j 个模型协方差为：

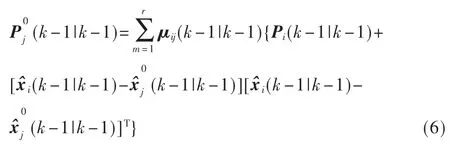
模型输入交互结果为r 个滤波器提供输入。

1.2 模型滤波输出[4-6]

滤波器是基于卡尔曼滤波原理，利用观测空间得到的结果更新状态空间的目标信息，是最小均方误差估计，方程如下：

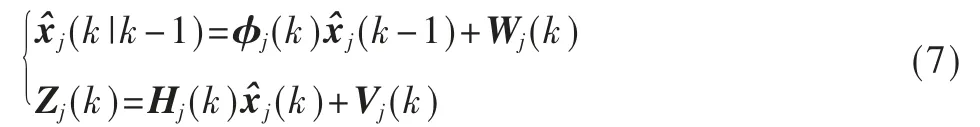
其中：j 表示第j 个模型；xj(k)是k 时刻系统状态变量，是dj×1 维列向量，dj为目标状态维数；Zj(k)是k 时刻的系统量测变量，是nj×1 维列向量，nj为观测向量维数；φj(k)是状态转移矩阵，是dj×dj矩阵；Hj(k)是测量矩阵，是nj×dj矩阵；Wj(k)是高斯型模型白噪声，0 均值，协方差为Qj(k)，是dj×dj矩阵；Vj(k)是高斯型量测白噪声，0 均值，协方差为Rj(k)，是nj×nj矩阵。滤波器输入是基于混合初始状态估计(k-1|k-1)和协方差(k-1|k-1)，应用卡尔曼滤波计算k 时刻模型j的状态估计(k|k)和协方差Pj(k|k)。

状态预测：

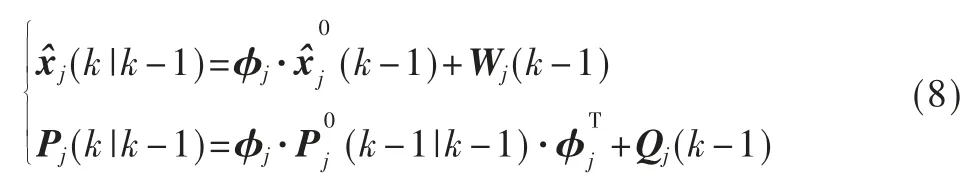
状态更新：

其中kj(k)是增益矩阵，vj(k)是残差，Sj(k)是残差协方差矩阵。从而，模型j的状态概率分布可以表示为(dj为模型维数)：

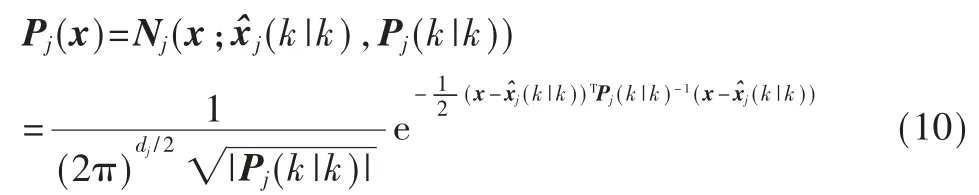
本步骤完成了各滤波器对目标状态分布估计。

1.3 模型结果融合输出[6-8]

传统IMM 算法是用各个模型滤波结果与模型概率加权乘积求和后得到目标状态分布更新，所以IMM 是一种趋势控制正确的近似估计，而不是统计意义下的最优估计。本文采用贝叶斯后验估计融合方法得到最优后验概率分布估计，在第2 步中得到各个模型的卡尔曼滤波状态矢量，每一个结果代表了模型后验概率目标分布估计，根据式(9)得到第j 个模型的目标状态后验概率分布为，Pj(k|k))，那么根据贝叶斯估计原理，由r个滤波模型同时产生的目标状态后验分布可表示为：P(x(k|k)|x1(k|k)，…，xr(k|k))，由于各个模型间是相互独立多维高斯分布，因此有：

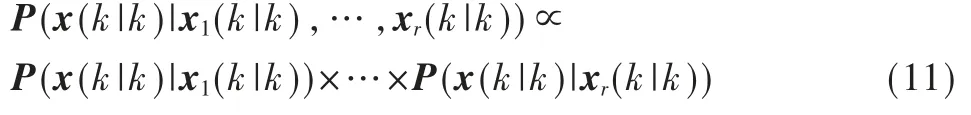
根据贝叶斯估计原理，最佳估计就是后验概率分布的期望，即：

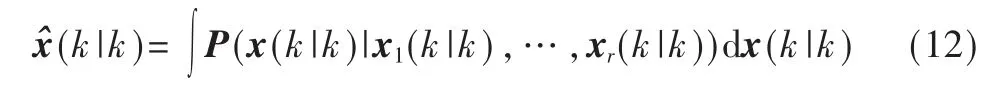
而对于模型j，由式(10)得到概率表达式为：

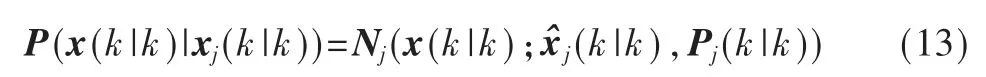
从而结合式(10)，得到融合后状态分布显式表达，得到融合期望均值和协方差如下：

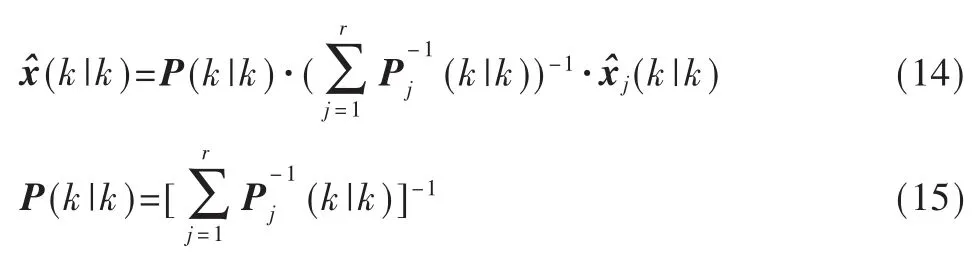
本步骤完成了目标状态融合，获得了贝叶斯后验概率分布的最优估计。

1.4 模型概率更新

传统的IMM 算法中，模型概率更新是通过残差及协方差，计算残差的似然度，再结合模型输入交互概率来计算模型概率，没有考虑多模型交互更新后的目标分布。本文用多模型融合后的目标状态分布计算各个模型似然函数，可以消除部分状态预测误差和观测值误差影响，提高模型准确度。在第3 步，多模型融合结果输出代表了最优贝叶斯后验估计的目标状态分布，以各个模型滤波结果在融合输出分布的似然函数，作为模型概率更新的似然度，来更新模型概率，根据似然函数公式，模型j的似然函数计算为：

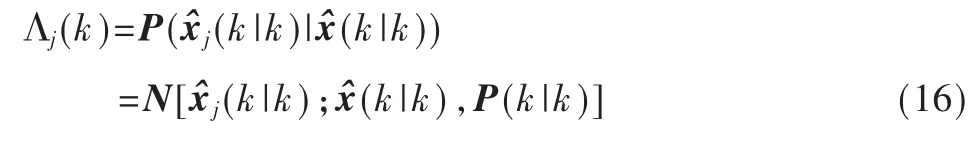
以uj表示模型概率，根据概率空间完备性总和为1，即：

概率空间由似然函数构成，所以概率空间根据模型似然度归一化为：

本步骤完成了模型概率更新计算，为1.1 节k+1 时刻计算模型转移概率提供了输入。

1.5 模型间转移概率计算

传统的IMM 算法中，马尔可夫概率转移矩阵是固定取值。本文提出了以各个模型滤波值为中心，各个模型滤波输出结果代表了该处理方法对目标状态分布的估计，模型交互定义为各个模型处理的结果在其他模型输出分布的似然函数，作为模型转化概率更新值。即模型i的滤波值在模型j的目标状态分布似然函数，作为模型i 在模型j的概率分布；模型j 自身的似然度由自身模型计算，从而模型i 到模型j的似然函数为：

πij表示模型i 到模型j的转移概率，j 取值1 到r，根据概率空间完备性概率总和为1。

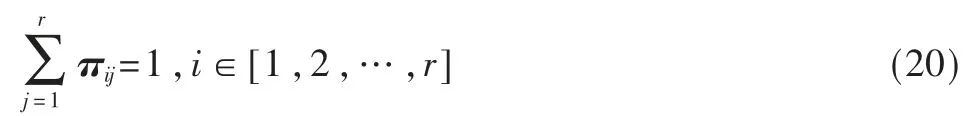
概率空间由模型似然函数构成，所以模型转化概率由似然度归一化，从而有：

本步骤得到模型间转移概率，为1.1 节提供了k+1时刻时变Markov 转移概率矩阵。

2 时变IMM与常规IMM 方法仿真比较

2.1 仿真场景设计

时变IMM 融合方法与常规IMM 方法进行了蒙特卡罗仿真对比，模拟两类不易跟踪的目标场景，强机动目标场景和强扰动静态目标场景，进行了50 次随机航路的仿真。首先根据Kalman 滤波原理，对目标状态空间和目标观测空间建模。

(1)目标状态空间建模

机动目标的运动模型可以通过具有加性加速度高斯噪声的统计来描述，所以本文采用匀速目标状态叠加加速度噪声模型来建模，通过控制参数和状态初始化，模拟产生强机动目标和静态扰动目标。

目标状态方程为：

w(k)的机动目标协方差矩阵为：

其中a 为加速度标准差，取值为0.2。

扰动静态目标协方差矩阵为：

其中a 为速度标准差,取值为0.2。△t 取值为0.5。

(2)目标观测空间建模

采用两种模型建立观测空间，模型1 是位置模型，模型2 是常速度模型对目标跟踪。观测目标状态为：

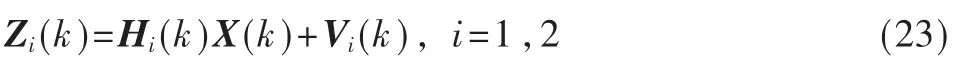
其中：模型1 观测矩阵H1=，模型1 观测噪声V1(k)的协方差矩阵为R1=b2，其中b 为模型1 观测误差，取值为0.5。

模型2 观测矩阵H2=，模型2 观测噪声V2(k)的协方差矩阵为R2=b2，其中b 为模型2观测误差，取值为0.5。

(3)常规IMM 算法马尔可夫转移概率矩阵：

2.2 仿真结果

2.2.1 强机动目标仿真结果

根据2.1 节的建模进行仿真，由于加速度较大，因此目标始终处于强机动状态，单次航路仿真跟踪曲线见图2，仿真了目标真实位置、模型1 跟踪、模型2 跟踪、时变IMM 融合跟踪、常规IMM 跟踪，共计5 条曲线，从图可见，4种方法都可以跟踪目标。图3 是航路误差统计。

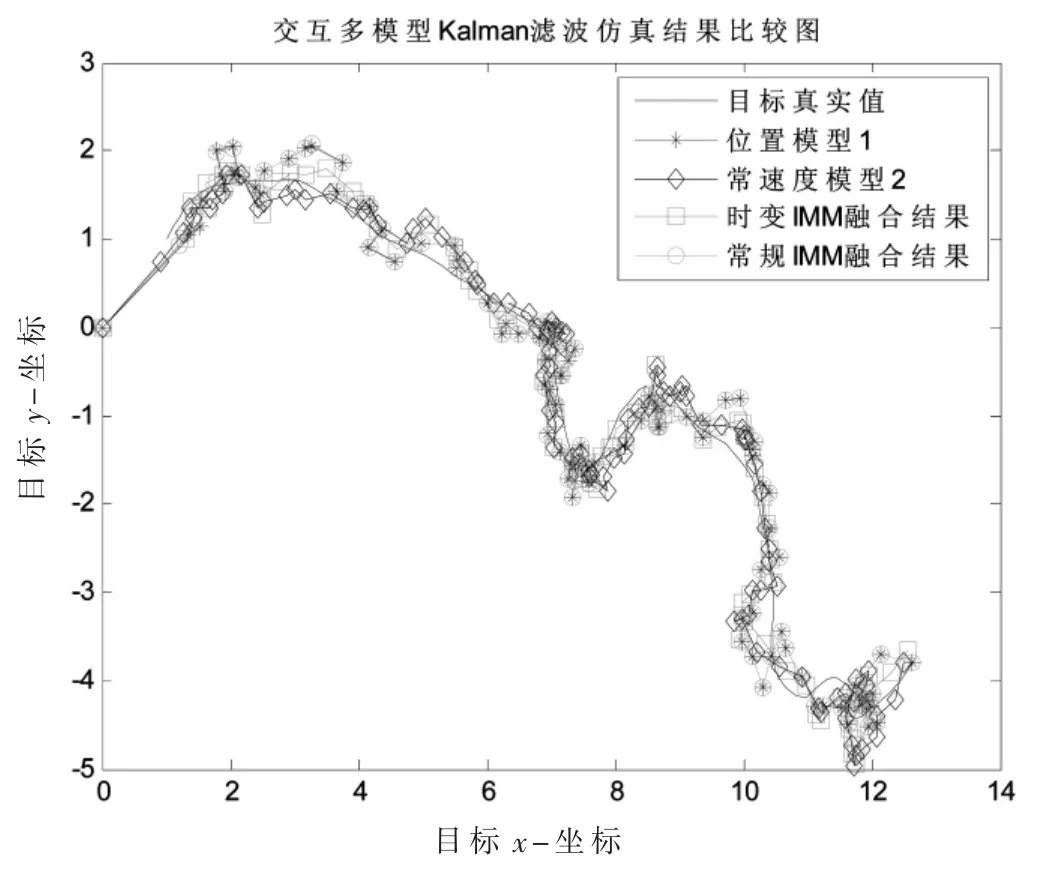
图2 强机动目标航路跟踪仿真结果图

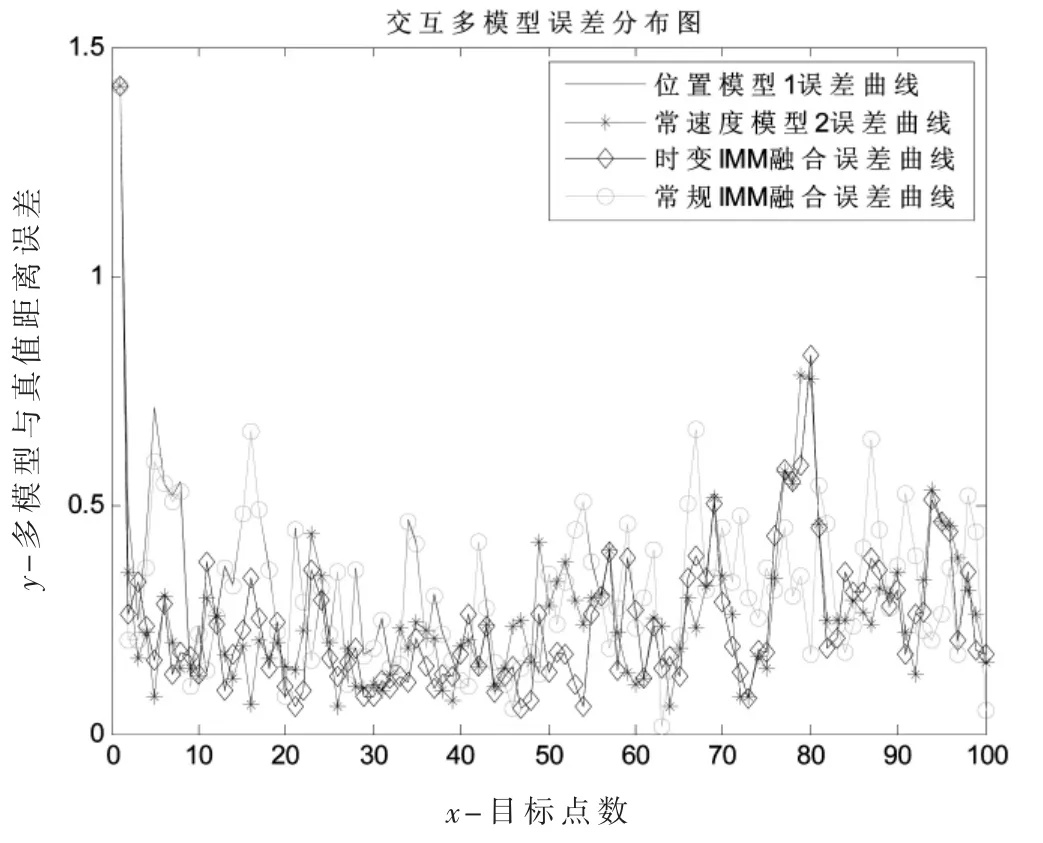
图3 强机动目标误差跟踪仿真结果图

强机动目标50 次随机航路蒙特卡罗仿真结果如图4 所示，可见时变IMM 融合方法效果最好，航迹误差曲线在最下方，而常规IMM 方法误差曲线介于两个模型之间。航迹误差统计分布结果见表1。

表1 强机动目标蒙特卡罗仿真结果分析表

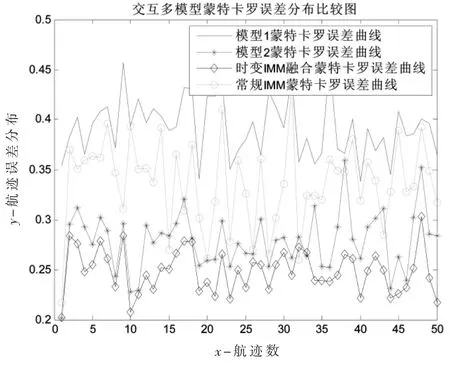
图4 强机动目标50 次蒙特卡罗误差仿真结果

2.2.2 强扰动静态目标仿真结果

强扰动静态目标一次航路仿真跟踪曲线见图5，从图5 可见，模型2 跟踪发散，模型1、时变IMM 融合和常规IMM 方法可以跟踪目标。图6 是航路误差统计，可见时变IMM 融合精度最好，常规IMM 精度在两个单模型之间。

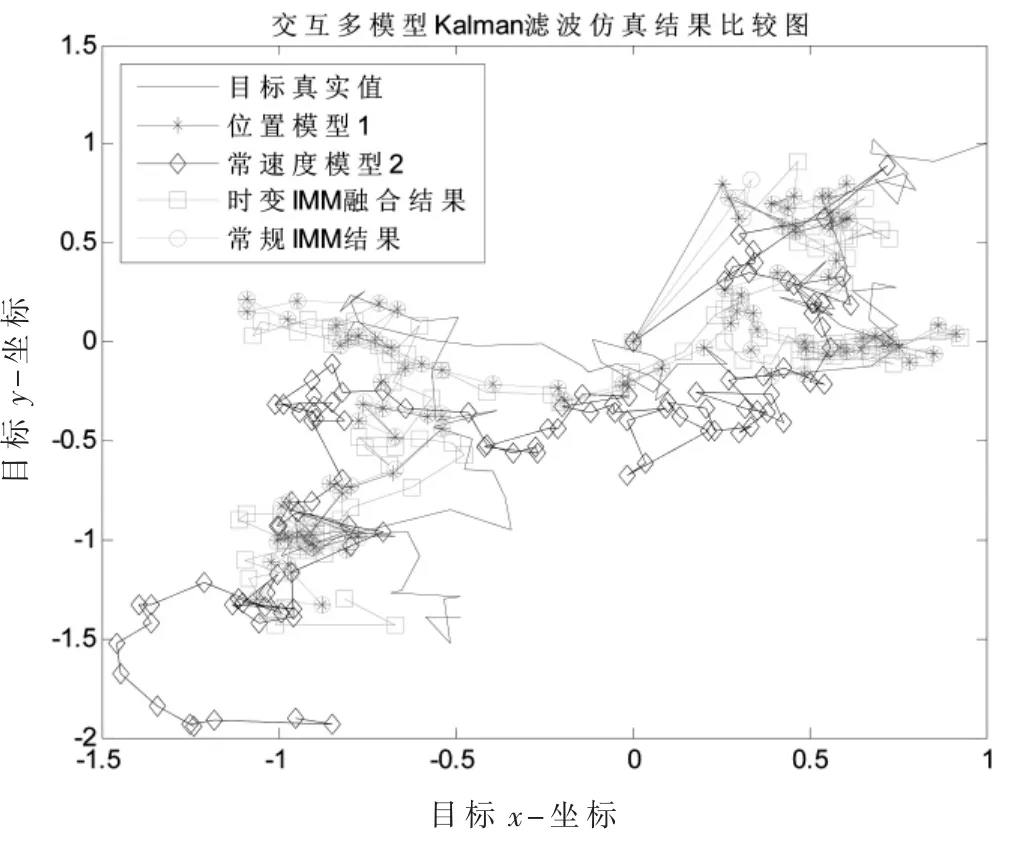
图5 强扰动静态目标航路跟踪仿真图

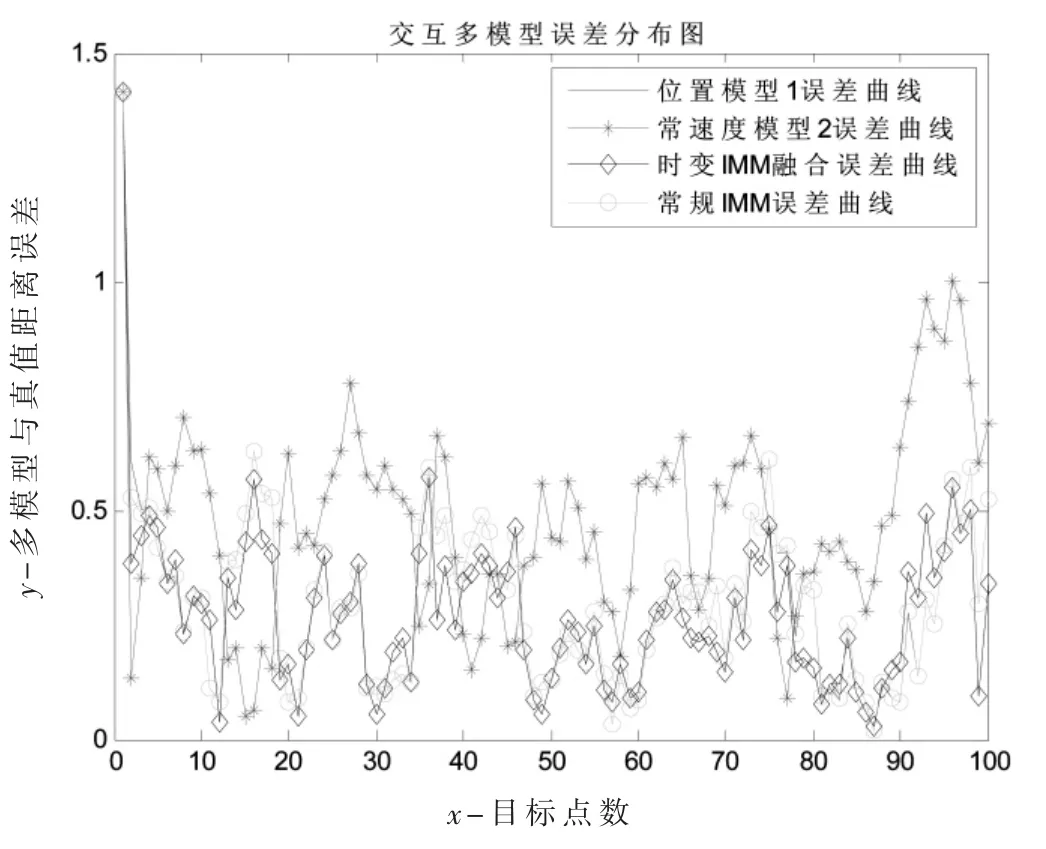
图6 强扰动静态目标误差仿真图

强扰动静态目标50 次蒙特卡罗仿真精度结果如图7所示，时变IMM 融合方法航迹误差曲线精度最好，分布在下方。统计的航迹误差分布结果见表2，时变IMM 融合效果显著。

表2 强扰动静态目标蒙特卡罗仿真结果分析表

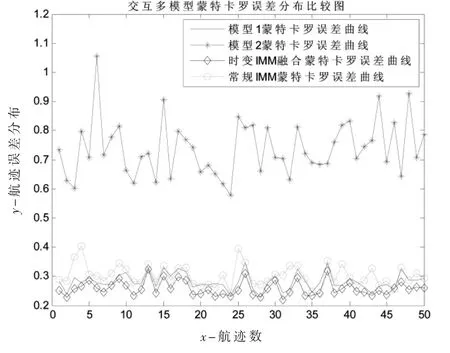
图7 强扰动静态目标50 次蒙特卡罗误差仿真结果

3 结论

本文应用似然函数理论实现了时变马尔可夫概率转移矩阵和目标模型概率更新方法，应用贝叶斯估计理论实现了多模型融合，得到目标最优贝叶斯后验准确估计。蒙特卡罗仿真结果验证表明，传统IMM 方法可以解决目标跟踪的连续性问题，但是并没有提高跟踪精度，相反时变IMM 融合方法不但解决了目标跟踪的连续性问题，还提高了跟踪精度。时变IMM 融合方法在航迹跟踪连续性、航迹误差和精度方面，统计结果都优于传统IMM 方法，原因是时变IMM 融合方法与目标实际状态更加吻合。所以理论和仿真结果都表明时变IMM 融合算法能更加准确及时地跟踪目标，对跟踪复杂机动目标有现实意义。