具有固定长度密文的广播加密方案

国佃利 ，杨鹏飞 ，刘家磊 ，王 萍 ，宋宁宁

(1.中国电子信息产业集团有限公司第六研究所，北京 100083；2.安阳师范学院 软件学院，河南 安阳 455000；3.中国联合网络通信有限公司北京市分公司，北京 100052)

0 引言

广播作为数据传输的重要方式，在有线电视、卫星通信、移动通信、计算机通信中有着广泛的应用。广播加密继承了广播中“一对多”的数据传输形式，是一种在不安全的信道中向指数量级用户发送密态数据的密码技术，指定授权集合中的用户可恢复出加密密钥，进而完成密态数据转换。即使全部非授权用户贡献出用户密钥，也无法通过获得广播数据加密密钥，该广播加密方案被认为能够抵抗完全合谋攻击。

广播加密方案的安全性可根据攻击模型定义分为两种类型：静态安全性与自适应安全性，满足上述两种安全性的方案均能够抵抗完全合谋攻击。在静态安全模型中，攻击者在知晓系统公钥前需公布挑战的授权集合，而自适应安全模型中则没有类似限制，实现自适应安全性往往需要牺牲部分加解密效率及大幅提升参数扩展量。实时数据广播加密系统是目前广播加密最为广阔的应用方向，如何提升其加解密效率与降低参数扩展量是亟待解决的关键问题。

平凡的广播加密方案的设计结构满足低存储空间需求和高安全性，能够抵抗完全合谋攻击。然而，平凡的广播加密方案有着极其庞大的密文扩展量。Fiat 和Naor[1]在1993 年提出了第一个广播加密方案，在该方案中用户数量为N，密文扩展量为N(tlog2tlog N)。值得注意的是，该方案仅仅能够抵抗不超过t 个用户发起的合谋攻击。显然，作者希望通过降低安全等级的方式以寻求降低平凡的广播加密方案中庞大的密文扩展量。2005 年，Boneh、Gentry 和Waters[2]利用素数阶对称双线性映射构造了可抵抗完全合谋攻击的广播加密方案，密文扩展量与密钥的扩展量都为O(1)，但系统公钥扩展量随着用户总数N 线性增长。Gentry 和Waters[3]在2009 年提出了新的广播加密方案，引入了半静态安全性，期望通过“双密钥”策略将半静态安全性转化为自适应安全性，该方案的密文的扩展量为O(1)。同年，Waters[4]基于对偶系统加密构造了适应性安全的广播加密方案，其密文扩展量为O(1)，但系统公钥和用户密钥扩展量都为O(N)。随后，多个研究人员利用多重线性映射构造了参数扩展量极低的广播加密方案[5-7]，但随着胡予濮教授[8]攻破了GGH 多重线性映射密码方案，基于该方案的广播加密方案均不再成立，在此不一一介绍。2015 年，Kim 等人[9]提出了基于身份的适应性安全的广播加密方案，但该方案的系统公钥和用户密钥均随着最大接收者总数线性增长，也就意味着即使授权集合中仅包含一个用户，也无法降低依据初始设定的最大接收者数量形成的各类参数扩展量。2019 年与2020 年，Guo 等人[10-11]分别提出了带认证性质的基于公钥的广播加密方案，并分别给出了静态安全性与自适应安全性证明，由于需要实现对消息发送者的鉴权认证，该方案的密文与密钥扩展量扩张十分庞大。

本文利用素数阶非对称双线性映射构造了基于公钥的广播加密方案，密文扩展量与用户密钥扩展量均为最优化的常数级别，公钥扩展量随着系统用户总数增加线性增长，随后在标准模型下基于非交互式的安全假设(co-Diffie-Hellman 假设)给出了静态安全性的证明。

本文首先简要描述素数阶非对称双线性映射及co-Diffie-Hellman 安全假设。随之，提出了一个新的广播加密方案，并证明了方案的静态安全性。

1 基础知识

下面简要描述素数阶非对称双线性映射以及判定性co-Diffie-Hellman 问题的定义[12-14]。

1.1 素数阶非对称双线性映射

映射e：G1×G2→GT为素数阶段非对称双线性映射，其中G1、G2和GT为3 个阶为大素数p的乘法循环群，满足以下3种特性。

(1)双线性 特性：对于∀g∈G1，∀h∈G2和∀a，b∈Zp，有等式e(ga，hb)=e(g，h)ab成立。(2)非退化特性：∃g∈G1，∃h∈G2，满足e(g，h)≠1。(3)高效计算特性：对于∀g∈G1，∀h∈G2，能够高效地计算e(g，h)∈GT。

1.2 判定性co-Diffie-Hellman 问题

利用安全参数λ 素数阶非对称双线性群生成器输出3 个阶为q的乘法循环群G1、G2和GT，以及非对称双线性映射e：G1×G2→GT。给定攻击者D={G1，G2，GT，e，ga，h，hb，T}，其中g ∈G1，h ∈G2，a，b ∈Zp。通过判定输出β∈{0，1}区分T 为gab或者为循环群G1中的一个随机的生成元。

定义1如果判定性co-Diffie-Hellman 问题在多项式时间内是难解的，即不存在多项式时间算法能够以不可忽略的优势ε 解决该问题。

2 广播加密方案

2.1 广播加密系统定义

广播加密方案包括以下4 个随机化算法：Setup，KeyGen，Enc，Dec[13]。

(1)Setup(N，λ)，该算法以用户总数N 为输入，输出结果为公私钥对。

(2)KeyGen(msk，u)，该算法主私钥和用户身份u∈[1，N]为输入，输出结果为用户u的私钥sku。

(3)Enc(S，PK)，加密算法以授权集合S⊆[1，N]和公钥为输入，输出结果为(Hdr，K)，其中Hdr 被称为头文件，K 为消息加密密钥。

消息M 利用对称加密方案在密钥K 作用下加密为密文C，最后广播密文为{S，Hdr，C}。

(4)Dec(PK，u，SKu，S，Hdr)，解密算法需要输入公钥PK、授权集合S、用户身份u、用户密钥sku以及密文头文件Hdr。如果u∈S，输出消息加密密钥K；否则，输出⊥。最后，用户u 利用密钥K 解密C 获取广播消息M。

在解密算法中，对于S⊆[1，N]以及u∈S，如果(PK，msk)是由Setup(N，λ)生成，sku是由密钥生成算法KeyGen(msk，u)生成，(Hdr，K)是由加密算法Enc(S，PK)生成，那么Decrypt(PK，S，u，sku，Hdr)=K。

2.2 广播加密方案构造

本小节在素数阶的非对称双线性群中构造了一个包含N 个用户的静态安全的广播加密方案，密文与用户密钥扩展量为O(1)，公钥扩展量为O(N)。新构造的静态安全的广播加密方案主要包括Setup、KeyGen、Enc、Dec 4 个算法。

(1)Setup(N，λ)，输入用户总数N与安全参数λ。算法生成两个阶同为大素数p的双线性群G1和G2，随机选取生成元g∈G1，h∈G2，并选取随机数α，γ∈Zp，同时依次计算hi=h(αi)(i=1，2，…，N，N+2，…，2N)，v∈gγ。最终输出系统公钥参数PK={h，h1，h2，…，hN，hN+2，…，h2N，v}以及主私钥msk={γ，α}。

(2)KeyGen(msk，i)，输入用户身份标识i ∈[1，N]，输出该用户的私钥ski=＝g(γαi)。

(3)Enc(S，PK)，广播者任意选取广播用户添加至授权用户集合S⊆[1，N]，在加密算法中输入系统公钥及授权用户集合S，随后加密算法随机选取数值t∈Zp，并计算消息加密密钥K与头文件Hdr，K=e (ski，hN-i+1)t=e(g，h)(tγαN+1)，Hdr=(C0，C1)=

最后，广播者利用对称加密算法对广播内容进行加密，在消息加密密钥作用下计算得到广播密文C=SymEnc(M，K)。

(4)Dec(PK，j，skj，S，Hdr)，输入接收者的身份标识j、接收者私钥skj、系统公钥、授权集合S 及密文头文件Hdr。如果接收者j∈S，解密算法按照如下算式计算消息加密密钥K；否则，输出⊥。

如果接收者属于授权用户集合，其可利用已得到的消息加密密钥K 解密广播密文获得广播消息M=SymDec(C，K)。

3 安全性证明

3.1 静态安全性模型

在静态安全性模型中，敌手A 被允许适应性地查询挑战集合S*外的用户私钥，意味着敌手能够掌握除挑战集合S*外的所有用户私钥，因此隐式地模拟了完全合谋攻击。具体的静态安全性模型定义如下所示：

(1)Init，敌手A 公开想要挑战的目标用户集合S*。

(2)Setup，挑战者运行初始化算法Setup(N，λ)，并将算法输出的系统公钥PK 发送给敌手A。

(3)Secret Key Queries，随后敌手A 被赋予查询用户私钥的权利，如果被查询用户i ∈S*时，挑战者立即终止该实验；否则挑战者运行密钥生成算法KeyGen(msk，i)，并将生成用户密钥ski发送给敌手A。如果敌手A 重复查询用户i的密钥时，挑战者不再运行密钥生成算法，只将已生成的用户密钥ski发送给敌手A。

(5)More Secret Key Queries，敌手A 获取后被允许继续查询挑战集合S*外的用户密钥。

(6)Guess，如果挑战者在密钥查询阶段没有终止实验，敌手A 需返回对比特β的猜测β′∈{0，1}。

如果敌手在Guess 阶段返回的猜测β′与挑战者在Challenge 阶段随机选取的比特β 一致，则意味着敌手A赢得了该实验，并攻破了广播加密方案。

定义2令敌手A 能够赢得广播加密方案的优势=|Pr[β′=β]-1/2|，对于任意多项式时间的敌手A，如果是一个关于λ的可忽略的函数，该广播加密方案可满足静态安全性。

3.2 静态安全性证明

基于上述定义的静态安全性定义，在标准模型下证明了本文构造的广播加密方案在判定性co-Diffie-Hellman 假设下满足静态安全性。判定性co-Diffie-Hellman假设为一般性静态安全假设，其与敌手所做的密钥查询次数无关，将广播加密方案的安全性归约至此类安全性假设更为合理。

定理1如果不存在多项式时间敌手A 能够以不可忽略的优势解决判定性co-Diffie-Hellman 问题，本文中构造的广播加密方案满足静态安全性。

证明：本小节利用反证法证明定理1，即如果多项式时间敌手A 可在不可忽略的优势下攻破新构造的广播加密方案，那么就能够依托该敌手打造解决判定性co-Diffie-Hellman 问题的算法B。算法B 通过已取得的{G1，G1，GT，e，ga，h，hb，T}与敌手A 进行多轮次的交互模拟实验。

首先，敌手A 选取目标用户集合S*，并将其发送给算法B。值得注意的是，算法B 在该试验中承担挑战者的角色。

随后，算法B 选取随机数α∈Zp，并计算hi=h(αi)，i=1，2，…，N，N+2，…，2N。随后令v=ga，并将计算得到的参数{h，h1，h2，…，hN，hN+2，…，h2N，v}发送给敌手A。由于ga的随机性隐含了数值a的随机特性，算法B 使用a 模拟了系统主密钥，但无法确定其准确数值。即使敌手A对上述公共参数后进行分析，也无法区分其与真实方案中的系统公钥的差别。

敌手A 在接下来的实验中被允许查询目标用户集合S*外的用户私钥，A 可将用户身份发送给算法B，随后B 利用已选取的随机数α∈Zp以及ga计算得到ski=(ga)αi。值得注意的是，如果敌手A 重复查询同一个用户的私钥，算法B 只能返回第一次计算得到的私钥。

在挑战阶段，算法B 在目标用户集合S*作用下计算挑战密文头及对应的消息加密密钥：

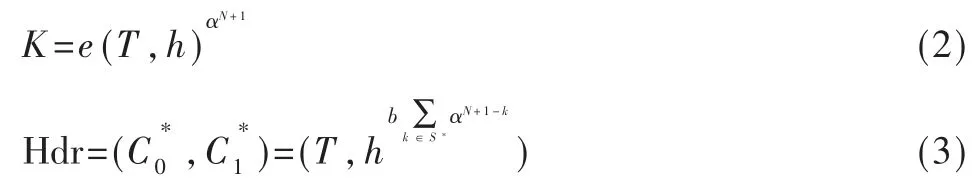
敌手A 获取挑战密文头与消息加密密钥后，会根据已得到的信息返回算法B 一个比特值β，算法B 用于解决判定性co-Diffie-Hellman 问题。

通过以上实验交互，算法B 借助敌手A的能力实现了对于新提出的广播加密方案的模拟，并在其中嵌入了判定性co-Diffie-Hellman 问题，一旦算法B 能够以不可忽略的优势解决判定性co-Diffie-Hellman 问题，那么敌手A 就能够以同样的优势攻破新提出的广播加密方案。通过反证法得出结论，由于判定性co-Diffie-Hellman 问题在多项式时间内是难解的，因此本文提出的广播加密方案满足静态安全性。

4 结论

本文利用素数阶非对称双线性映射设计了一个满足静态安全性的广播加密方案，其中密文扩展量与用户密钥扩展量均为固定长度，系统公钥扩展量随着用户总数线性增长，随后给出了形式化的安全性证明。新提出的广播加密方案系统公钥扩展量仍十分庞大，在未来的研究中希望通过采用新的密码学工具及安全假设构造更为安全的广播加密方案，在保证参数扩展量优化的同时进一步提升安全特性。