朴实中探究本质 简约中凸显思维
李永卫


几何综合题是中考热点问题之一,下面以大连市2020年中考第25题为例探索解决这类问题的思路与方法.
原题重现
[原题重现]
如图1,△ABC中,点D,E,F分别在边AB,BC,AC上,BE = CE,点G在线段CD上,CG = CA,GF = DE,∠AFG = ∠CDE.
(1)填空:与∠CAG相等的角是 ;
(2)用等式表示线段AD与BD的数量关系,并证明;
(3)若∠BAC = 90°,∠ABC = 2∠ACD(如图2),求[ACAB]的值.
[破解策略]
第(1)问:根据等边对等角回答即可.
第(2)问:有多种解题策略.可由已知条件中的“一边一角”来构造全等、平行四边形;由线段中点,可以想到利用“中线倍长”或三角形“中位线”来解题.
第(3)问:看到题中给出了二倍角,一定要迅速回想二倍角的转化方法,同时,题中给出90°角,借助图形可以想到绝配角的运用,进而添加辅助线,建立出绝配角基本图形,再通过设元,结合勾股定理,表示出两条线段,进而求出比值.
解:(1)∵CA = CG,∴∠CAG = ∠CGA. 故答案为∠CGA.
(2)这一问有36种解题方法,下面给出其中6种,其余解法请关注公众号获得.
策略一:突出“一边一角构造全等”
解法1:AD = [12]BD. 理由:
如图3,在CD上取中点M,截取DN = AF,连接EM,EN,
∵DE = GF,∠CDE = ∠AFG,∴△END ≌△GAF(SAS),
∴EN = GA,∠END = ∠GAF.
∵∠CAG = ∠CGA,∴∠CGA = ∠END,∴∠AGD = ∠ENM.
∵BE = CE,DM = CM,∴EM是△BCD的中位线,
∴EM[⫽]BD,EM = [12]BD,∴∠ADG = ∠EMN,
∴△ADG ≌△EMN(AAS),
∴EM = AD,∴AD = EM = [12]BD.
解法2:如图4,取BD的中点M,连接EM,在EM上截取EN = AF,由三角形中位线得ME[⫽]CD,得到△DEN ≌△GFA,△DMN ≌△ADG. 具体过程请同学们自己完成.
解法3:如图5,作AQ[⫽]DE,交CD于点Q,取BD的中点P,连接PE,得到EP[⫽]CD,进而得到△AGQ ≌△GAF, △AQD ≌△DEP,具体过程请同学们自己完成.
解法4:如图6,作EM[⫽]BA交CD于M,EN[⫽]AC交CD延长线于N,可证△CFG ≌△NDE,△NEM ≌△CAD,进而得EM是△BDC的中位线. 具体证明过程请同学们自己完成.
策略二:突出“倍长中线”
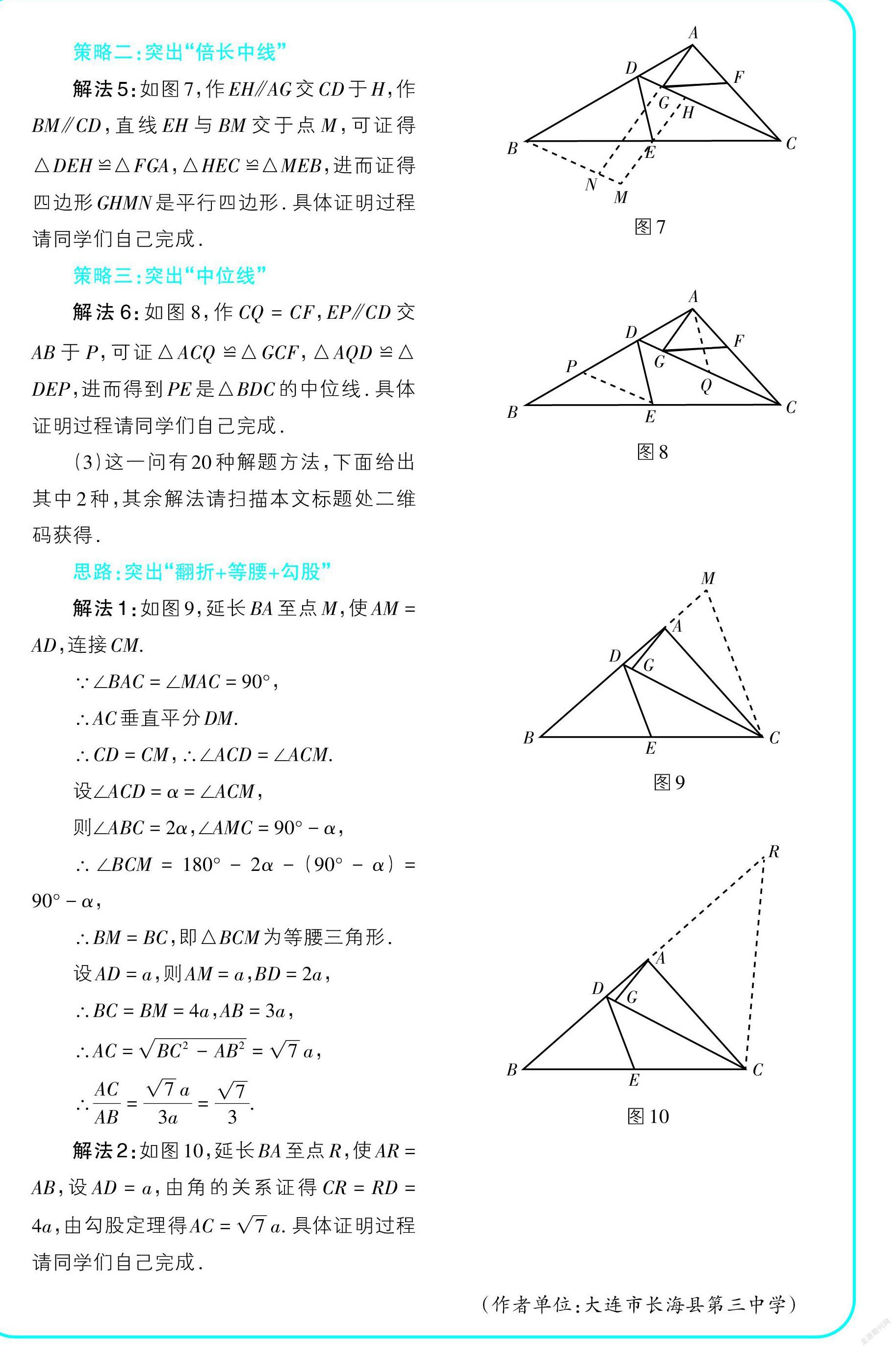
解法5:如图7,作EH[⫽]AG交CD于H,作BM[⫽]CD,直线EH与BM交于点M,可证得△DEH ≌△FGA,△HEC ≌△MEB,进而证得四边形GHMN是平行四边形. 具體证明过程请同学们自己完成.
策略三:突出“中位线”
解法6:如图8,作CQ = CF,EP[⫽]CD交AB于P,可证△ACQ ≌△GCF,△AQD ≌△DEP,进而得到PE是△BDC的中位线. 具体证明过程请同学们自己完成.
(3)这一问有20种解题方法,下面给出其中2种,其余解法请扫描本文标题处二维码获得.
思路:突出“翻折+等腰+勾股”
解法1:如图9,延长BA至点M,使AM = AD,连接CM.
∵∠BAC = ∠MAC = 90°,
∴AC垂直平分DM.
∴CD = CM,∴∠ACD = ∠ACM.
设∠ACD = α = ∠ACM,
则∠ABC = 2α,∠AMC = 90° - α,
∴∠BCM = 180° - 2α - (90° - α) = 90° - α,
∴BM = BC,即△BCM为等腰三角形.
设AD = [a],则AM = [a],BD = 2[a],
∴BC = BM = 4[a],AB = 3[a],
∴AC = [BC2-AB2=7a],
∴[ACAB=7a3a=73].
解法2:如图10,延长BA至点R,使AR = AB,设AD = a,由角的关系证得CR = RD = 4a,由勾股定理得AC = [7a]. 具体证明过程请同学们自己完成.

