顺势而为，合理建构，打造生长型活力课堂

汤忠芳

摘要

针对现有数学复习课模式的缺点，以实际教学为例，探究有效复习的策略，合理建构，以培养学生勇于质疑和善于思考的习惯，让学生在综合运用知识和方法解决问题的过程中，发展创新意识和实践能力。

关键词

初中数学 复习课 建构

数学复习课一般分为揭示目标、再现知识、梳理沟通、深化提高四个阶段。一直以来，“概念梳理+练习强化”是初中数学复习课的普遍模式。这种模式的缺点是：学生只顾做，教师不去想。这使得复习课变成了简单机械的知识点的重复，而忽視了对学生能力的培养。因此，笔者认为，复习课的教学设计应结合相关知识点，选择典型例题，通过设计问题串，层层推进，由浅入深地展开教学;努力构建整体认知体系，帮助学生将“零散”的知识点编织成知识的“互联网”，让知识融合、内化，从而在知识重构的过程中，培养学生提出问题的思考力和解决问题的创新力。

下面，笔者以“矩形中的折叠问题”为例进行具体分析。

一、顺势而为：习题呈现及评析

1.呈现基本问题，“铺设平台”建构。

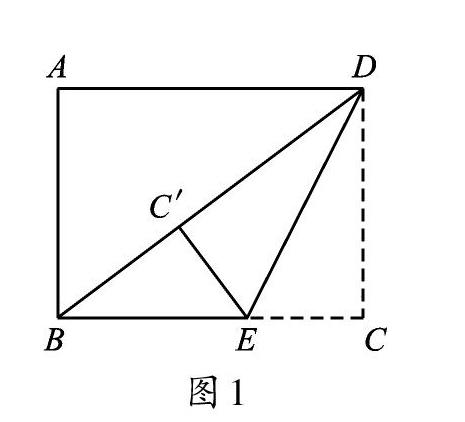
问题1：如图1，在矩形ABCD中，AB=6，AD=8，点E是BC边上一点，将△DCE沿DE折叠，使点C的对应点C′恰好落在对角线BD上，求CE的长。

教学分析：这是一道常规的矩形折叠问题，学生只要发现折叠过程中的不变量（对应线段相等），就可以通过设未知数，利用方程思想并借助勾股定理解决。因此，教师可以从学生较为熟悉的题型切入，借助学生已有的经验，利用常规的解题思路，设计出关联度较高的问题，以此来培养学生的发散思维，让学生从“会解”向“会思”转变，由“会思”向“会学”突破，激发学生学习数学的兴趣和热情。

2.逐层递进，“生长融合”建构。

问题2：在上述问题中，若点C在翻折过程中落在矩形ABCD的对角线上，其余条件不变，求CE的长。

问题3：在上述问题中，若点C 在翻折过程中落在矩形ABCD的对称轴上，其余条件不变，求CE的长。

教学分析：问题2和问题3是典型的分类讨论问题。因为矩形有两条对角线和两条对称轴，所以解决这类问题，就要以此作为讨论的依据，画出符合条件的图形，构造直角三角形，再联系“一线三等角”等知识点，通过相似三角形和勾股定理来解决。这两个问题是问题1的拓展与延伸，设置的目的是通过情况的多样性，从一般到特殊，引导学生进行分类讨论，使学生的知识结构得到生长，让学生在解题时积累解决折叠问题的经验，掌握学习数学的方法，促进学生的认知结构化、序列化。

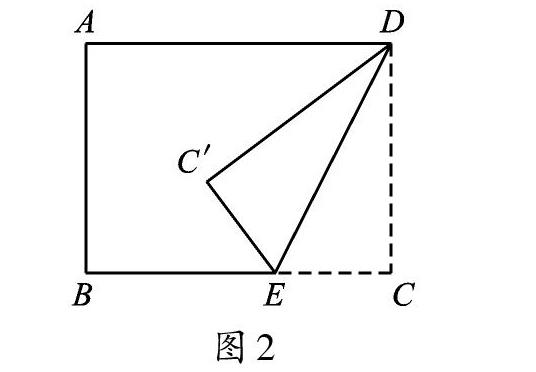
问题4：如图2，在上述问题中，连接BC′，若BC′∥DE，其余条件不变，求CE的长。

教学分析：所求的问题不变，通过折叠过程中折痕与对应点位置的特殊性，利用三角形相似等方法，不断巩固和强化“折叠问题”，引导学生有序思考，使学生既掌握学习数学的“道”，又能悟出学习数学的“理”，使知识和方法趋于系统化，逐步提升学生的学习能力。

3. 变式拓展，“完善整合”建构。

学生经过自主探究和小组交流，在对上述问题的研究过程中，不难发现，折叠时还会出现下列具有代表性的图形。

面对折叠问题中情况的复杂性和多样性，我们有必要抓住问题的核心进行梳理和归类。从折痕来看，发现“C′经过矩形顶点、经过对称中心、在对角线上、在对称轴上”等情况是最常见的特例;从对应顶点C′的位置来看，发现“顶点C′落在矩形内部、矩形边上、矩形外部”是最常见的特例;综合来看，折叠问题的本质是全等变形，折痕可看作线段的垂直平分线，也可看作角平分线。通过自主整理和归纳（见表1），学生能够找到问题研究的切入点和解决问题的一般方法。在不断生成新问题和解决新问题的过程中，学生对知识的认识和理解才会更深刻。这种层次化、渐进式的学习过程，必定会给予学生更精彩的思维碰撞和更丰富的学习经历。

二、合理建构：精准施教的实践与思考

数学对象不是孤立存在的，而是整体数学结构中的一部分。数学建构是一种通过知识脉络将知识点进行结构化的组织和加工，并逐步融合，最终形成知识网络的过程。在进行复习课教学时，教师应在选择适当的数学模型帮助学生梳理知识的同时，关注知识的形成过程，逐步建构，精准施教，这既有助于学生全面系统掌握知识，形成体系，促进数学理解，凸显核心素养，又能提升学生学习数学的自信心，有益于高效数学课堂的构建。

1.目标精准：知识生长，能力提升。

生长源的选择是数学复习课的核心。生长源可以是某个核心知识点（重点、疑点、难点）或某种解决问题的策略与方法。复习课的教学设计要紧扣源问题，在学生已有的认知基础上，进行变式、拓展与延伸;通过类比等方式，进行知识的迁移和升华。本节课中的问题1就是教材中的习题，以此为基础展开的教学，起点低，是为了发展学生的“四基”;再通过问题2和问题3的延伸和拓展，将知识纵向发展，重建知识结构，在学生领悟重要数学思想的同时，提升学生的思维能力。

2.问题精准：层层深入，系统建构。

建构的切入点不宜过大，问题的选择要具有典型性。层层深入、螺旋上升是建构的关键。本节课就是从一道题切入，引领学生研究一类题型，以学为中心，着眼于学生的最近发展区，由易到难，由低阶思维转变到高阶思维;通过问题串，追溯问题本质，从而建构起“矩形折叠问题”的数学模型，在层层抽丝剥茧的教学智慧中，促进学生知识链的生长。

3.练习精准：问题导向，强化应用。

从复习课的实效性出发，练习的设计要关注梯度和广度。从“模仿”→“再造”→“创造”的理念出发，习题的设计要讲究层次性和整体性;要提倡题组教学，根据知识的内在联系，有的放矢地设计练习。我们既要关注学生对知识技能的掌握，又要关注学生思维的训练和能力的培养，以习题的针对性和有效性，促进学生主动学习、创造性学习，从而促进学生可持续能力的培养。

4.讲评精准：思路点拨，方法多样。

教深、讲透是复习课的教学追求。教师讲评习题时，要注意语言的科学性和规范性，不能仅仅教学生求出答案就完事儿。教师需要深度研题，开展一题多问和一题多解教学，对比不同思路和解法的优劣，然后基于学生立场，选择最适切的解法进行讲解，让学生知其然，更知其所以然。师生共同追求讲评品质的提升，以习题教学的讲透与教深为目的，促进学生学活、学透和学深。

发展数学思维，彰显有价值的教学，是数学教师的教学价值追求。教师在设计复习课教学时，研究起点应低一点，探索步子应大一点，发展眼光应远一点，从学生角度去发现问题，探究问题。通过题型归类、模型构建等方式，展开数学课堂的生长型教学活力建构，有助于培养学生勇于质疑和善于思考的习惯，让学生在综合运用知识和方法解决问题的过程中，发展创新意识和实践能力。

（作者单位：江苏省常州市金坛区茅麓中学）