利用滩坝砂体规模研究古风力的定量恢复*

王俊辉 姜在兴 鲜本忠 张春明 李国斌

1油气资源与探测国家重点实验室，中国石油大学(北京)，北京 102249 2中国石油大学(北京)地球科学学院，北京 102249 3中国地质大学(北京)能源学院，北京 100083 4中国石油勘探开发研究院，北京 100083 5中国石油勘探开发研究院西北分院，甘肃兰州 730020

古风场是古大气环流的直接结果，是古气候研究的重要内容(刘立安和姜在兴，2011；庞军刚和云正文，2013)。以往的古气候重建侧重于古温度和古湿度的恢复(Quanetal.，2011，2012a，2012b)，而古风场的研究则比较少。究其原因，主要是研究手段匮乏，难于挖掘保存有古大气流场信息的地质资料。

古风力的定量恢复是古风场恢复的难点。Eastwood等(2012)根据风成沉积物的粒度与风的搬运能力之间的定量关系，提出了一种比较可靠的基于沉积动力学原理恢复古风力的方法。利用风的直接产物——风成沉积的方法尽管比较可靠，但是地质记录中保留下来的风成沉积物却并不多见，限制了该方法的大范围应用。此外，由于受空气搬运能力的限制，地质历史中保留下来的大多数风成沉积物粒度一般不超过粗砂级，即使通过这些最粗的风成沉积物所恢复的古风力也不会超过12m/s，超过此强度的风极少能通过风成沉积物记录下来(王俊辉等，2018)。

风除了直接作用于沉积物，还可以驱动其他介质运动，在沉积物中留下可以重建古风力的线索。面积广阔的地表水体就是一种常见的联系风力和沉积物的介质(刘立安和姜在兴，2011)。风作用于水体会产生波浪，所形成的波浪的大小主要取决于风力大小(Orme and Orme，1991)，并且存在统计学上的经验关系。因此，古风力的恢复，在一定程度上可以通过古波况的恢复来间接完成。

许多学者自20世纪70—80年代始就意识到通过滨岸带沉积物可以为古波况的恢复提供线索(Tanner，1971；Allen，1981，1984；Dupré，1984；Diem，1985)。随后，Orme 和 Orme(1991)、Adams(2003，2004)、Knott等(2012)等利用滨岸带最粗的沉积颗粒反映波浪搬运能力的原理，在古波况恢复的基础上恢复了古风力。然而，这种方法对资料要求较高，比较适合于露头研究。对于以地下资料为主的钻孔资料，其应用受到限制(王俊辉等，2018)。

波浪在向岸边传播的过程中，会在滨岸带形成滩坝沉积(姜在兴等，2015)，所形成的滩坝砂体的规模取决于波浪大小，进而取决于风力的大小(李国斌，2009；李国斌等，2010；王俊辉，2016)。基于此，近年发展了2种较完善的利用滩坝砂体恢复古波况和古风况的方法(王俊辉，2016): (1)利用破浪沙坝恢复古风力(Jiangetal.，2018)；(2)利用沿岸砾质滩脊(沿岸砾质坝)恢复古风力(Wangetal.，2018)。作者在此2种方法的分析基础上，在操作流程、适用条件、误差分析等方面又做了更加完善的介绍和分析，以期对该研究工作有进一步的推动，也可供大家借鉴与应用。

1 风与波浪的关系

风所形成的波浪大小取决于风速、风时(指状态相同的风持续作用于水面的时间)、风程(指状态相同的风在水面作用的距离)3个因素(Komar，1998)。当风时足够长，波浪将达到定常状态，此时风浪(风所形成的波浪的简称，下同)的大小由风速和风程2个因素决定。因此，通过风浪大小推导风力(风速)时，风程的获取很重要。另外需要注意的是，在浅水条件下，由于水底摩擦力的作用，水深也会影响波浪大小(CERC，1984；滕学春等，1985)。因此，尽管表达风与波浪关系的经验公式有很多(滕学春等，1985；朱炳祥，1990)，但几乎都可以表达为波高、风程、水深的函数。

Adams(2003)根据美国海岸工程研究中心(CERC)的资料给出了一个相对简单的、应用于简单波况条件的有限风区水体的风浪关系公式：

(1)

其中，UA为风压系数；F为风程(m)；Hs为深水区有效波高(m；将给定波列中的波高由大到小依次排列，其中最大的 1/3 部分波高的平均值称为“有效波高”，也可记为H1/3)。

风压系数可以进一步根据经验关系转换为风速(CERC，1984；Adams，2003):

UA=0.71U1.23

(2)

其中，U即为水面上方10m处的风速(m/s)。

公式1和公式2表明，只要能够对地质历史时期的风程(F)和波况(Hs)进行恢复，则古风力的恢复将变得可行。下文将分别以破浪沙坝、沿岸沙坝与波况的对应关系为切入点，介绍利用2种类型沙坝恢复古风力的依据。

2 利用破浪沙坝厚度恢复古风力

2.1 破浪沙坝的成因

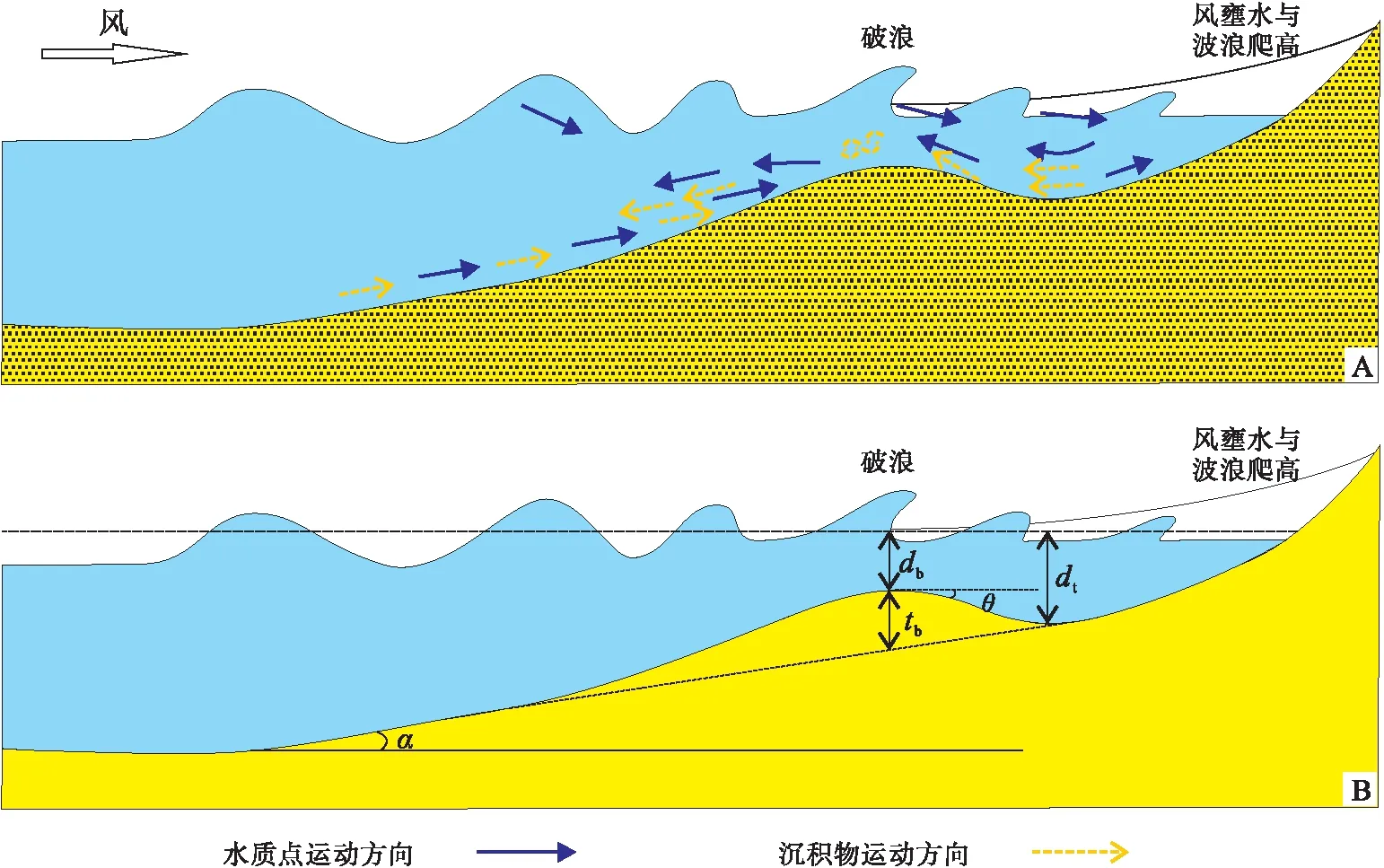
A—沉积物在破浪带集中形成破浪沙坝，最终其形态、规模与破浪将达到平衡状态；B—各参数示意： tb为破浪沙坝厚度(m)，dt为坝后凹槽水深(m)，db为沙坝水深或破浪水深(m)，α为滨岸带地形坡度角(°)，θ为沙坝向岸一侧的坡度角(°)图1 破浪沙坝的成因模型(据Davidson-Arnott，2013；有修改)Fig.1 Breaking wave model for the longshore bar formation(modified from Davidson-Arnott，2013)

波浪在向岸传播过程中遇浅会发生破碎形成破浪，在破浪处沉积物将聚集形成沙坝。破浪沙坝的破浪模型(breakpoint model)或自组织模型(self-organizational model)是已经广为接受的沙坝成因模型之一(Dyhr-Nielsen and Sorensen，1970；Coco and Murry，2007)。该模型认为，在破浪带中，破浪带向陆一侧产生的离岸搬运与向海(湖)一侧的向岸搬运，使沉积物在破浪带集中，形成沙坝，坝后形成凹槽。沙坝在水动力作用、沉积物搬运、沙坝形态演化的相互反馈作用下生长，最终达到平衡(Houser and Greenwood，2005)(图1)。沙坝的破浪成因机制是基于海洋滨岸环境提出的，研究表明，在中大型湖泊环境中同样适用(Greenwoodetal.，2006)。

根据破浪模型，破浪控制着破浪沙坝的离岸位置、规模及其产生的水深范围。很早就有研究表明，波浪越大，发生破浪的水深越大，形成破浪沙坝和坝后凹槽的水深也就越大(Komar，1998)。因此随着波浪的增强，破浪沙坝会向深水方向迁移，但沙坝最终仍会与破浪波高建立起平衡关系(Houser and Greenwood，2005；Price and Russink，2011；Davidson-Arnott，2013)，破浪沙坝的规模也会随着破浪的增大而增大(Pruszaketal.，1997)；相反地，随着波浪的减弱，破浪沙坝会向浅水方向迁移，沙坝的规模也会减小。

2.2 破浪沙坝的形态特征

大小不同的波浪形成的破浪沙坝规模不一，但沙坝的形态却相似(Davidson-Arnott，2013)。观测表明，破浪沙坝的横剖面具有明显的不对称性(图1-B)，表现为向陆地一侧的倾角明显大于离岸一侧，向岸侧的角度θ最大可能达到休止角(Davidson-Arnott and Greenwood，1974；Dabrio and Polo，1981；Thorntonetal.，1996；Gallagheretal.，1998)。另外，沙坝向岸一侧的槽谷水深dt(m)与坝顶水深db(m)之比Rtb，即：

(3)

具有一定的经验关系。例如，Otto(1912)和其他德国观测者在波罗的海的观测得出的平均值为1.66。Keulegan(1948)通过实验发现，Rtb平均为1.69，与Otto的观测较为吻合。但Evans(1940)通过描述Michigan湖的破浪沙坝，发现天然形成的沙坝较平坦而宽广一些，Rtb变化于1.42～1.55之间。也有人认为坝后凹槽的水深要比坝顶的水深大很多，Rtb可能达到3(Drønen and Deigaard，2007)。

2.3 破浪沙坝厚度与风力的关系

根据破浪沙坝与破浪之间的平衡关系，从破浪沙坝厚度这一参数入手，可以进行古波况的恢复，进而通过风浪关系，可以恢复古风力。

根据破浪沙坝的形态特征(图1)，沙坝厚度tb(m)、坝顶与坝后凹槽水深(分别为db，dt)、滨岸带地形坡度(tanα)、沙坝向陆一侧的坡度(tanθ)具有如下的几何学关系(图1):

(4)

将公式3代入，公式4可以简化为公式5:

(5)

因此，当沙坝的基座坡度角α(°)、与沙坝形态有关的参数Rtb、θ(°)等参数已知的条件下，就可以通过破浪沙坝厚度tb求得破浪水深db。根据db，可以进一步根据破浪关系求得破浪波高Hb(m)。

Hb=γbdb

(6)

其中，γb为破浪指数，表达了破浪波高与破浪水深之间的关系。γb在海岸工程领域中有着比较系统的研究，不同的学者对此也有不同的计算方法。Jiang 等(2018)在应用破浪沙坝恢复古风力时，对γb的计算采用了Goda曲线法。Goda曲线是Goda(1970)根据几种海滩坡度的试验资料绘制成的经验曲线，已被中国《海港水文规范2013》引用。Goda曲线给出了破浪指数γb与深水波波长L0(m)、地形坡度tanα之间的关系(图2)。

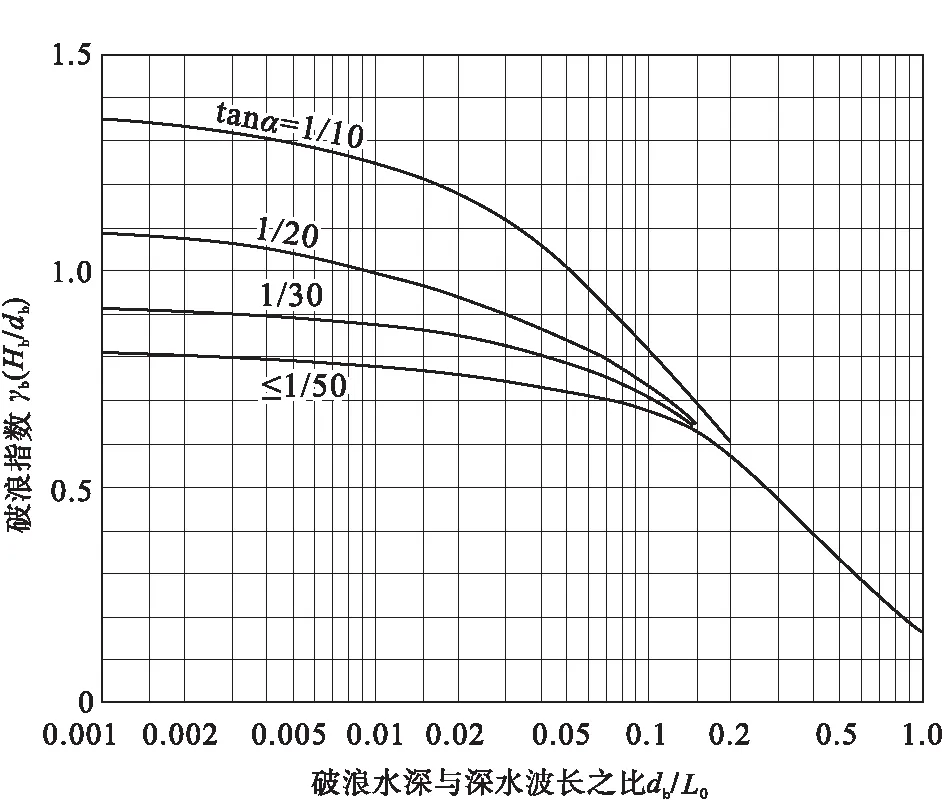
图2 破浪指数(γb)与破浪水深与深水波长之比(db/L0)、滨岸带地形坡度(tanα)经验关系曲线(据Goda，1970)Fig.2 Empirical relationship between the breaking wave ratio(γb)，the ratio between breaking wave depth and deep-water wave length(db/L0)，and the slope of the shoreface(tanα)(after Goda，1970)

在利用Goda曲线之前，需要预先估计深水波波长L0。目前，直接从地质记录中恢复L0难度较大(Diem，1985；Adams，2003，2004)。根据艾利波理论，深水波长L0可以近似地由波浪周期T(s)表达出来：

(7)

其中，g为重力加速度(m/s2)。同样地，从地质记录中恢复波浪周期T也比较困难。Adams(2003)给出了波浪周期(T)与风程(F)的大致关系(图3)。因此，通过对F的恢复，可以粗略地恢复T和L0。有了深水波波长L0、地形坡度tanα，可以进一步应用Goda曲线获取γb，进而通过破浪水深db这一参数获得破浪波高Hb(公式6)。

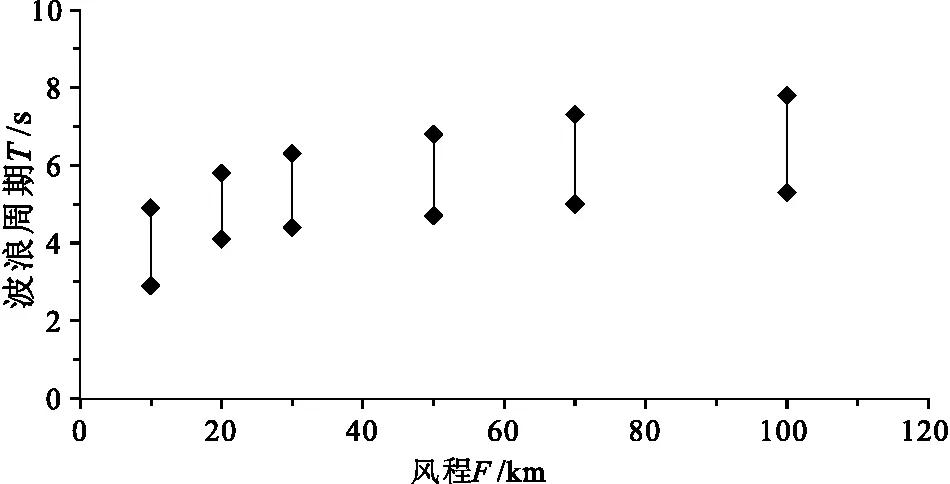
图3 波浪周期(T)与风程(F)的经验关系(据Adams，2003；有修改)Fig.3 Empirical relationship between wave period(T)and fetch(F)(modified from Adams，2003)

对于向岸传播的波浪，波高在破浪时达到最大。由此得到的破浪波高可以认为是对应于破浪沙坝形成时期波浪的最大波高(Hb≈Hmax)。假定该波高为相应深水波高的理论极限值，可以根据波浪的统计特征近似求得任意不同累积频率波高(Hp)(堤防工程设计规范；Sawaragi，1995)。例如，有效波高Hs可以近似为：

Hs≈0.5Hmax

(8)

根据有效波高，结合风程参数，即可以根据公式1 和公式2求得风力大小(即风速)。

因此，依据破浪沙坝恢复古风力，只需要从地质记录中获取以下参数： 单期次破浪沙坝的厚度tb、古地形坡度角α以及古风程F。据此，利用破浪沙坝厚度进行古风力恢复的基本步骤是： (1)准确识别出破浪沙坝，并测量出单期形成的破浪沙坝的最大厚度，如果破浪沙坝经历了显著的压实过程，应需进行去压实校正(Jiangetal.，2018)，以获得其原始厚度(tb)；(2)确定所研究的古湖泊的古地貌(如姜正龙等，2009；高艺等，2015)，从而得到古坡度角(α)；(3)确定相应时期的古岸线(如姜在兴和刘晖，2010；苏新等，2012)以及古风向，从而得到在风向方向上的古风程(F)；(4)根据破浪沙坝的厚度(tb)、地形坡度角(α)、风程(F)3个参数，计算破浪水深(db)(公式4)；(5)利用破浪关系，如Goda曲线法，将破浪水深转换为相应的破浪波高(Hb)；(6)将破浪波高转换为深水区有效波高(Hs)(公式8)；(7)根据公式1，利用深水区有效波高(Hs)与古风程(F)计算相对应的风压系数(UA)；(8)由风压系数计算出风速(U)(公式2)。具体步骤如 图4 所示。

3 利用沿岸沙坝厚度恢复古风力

3.1 沿岸沙坝(滩脊)的成因

向岸传播的波浪进入滨岸带后，在惯性力作用下冲向岸边，将形成“冲浪”，没有渗入沉积物中的水直接回头沿坡而下成为“退浪”或“回流”。在岸线附近存在一个“冲浪回流带”。

冲流与回流交替冲刷岸线。一方面，在冲浪作用下，沉积物将克服摩擦力、重力，向上运动；另一方面，在回流作用下，沉积物将克服摩擦力，向下运动。一般来讲，冲流的搬运能力要强于回流(Masselinketal.，2005)。因此，波浪有效地将最粗的沉积物搬运至岸线，形成沿岸线展布的沙坝，即沿岸沙坝(图5)，也称为滩脊或滩肩。最终沿岸沙坝的规模也反映了沉积物属性、风浪大小、地貌动力过程之间的平衡状态(Buscombe and Masselink，2006)。

图5 沿岸沙坝(滩脊)的形成示意图(据伍光和等，2008)Fig.5 Schematic illustration showing the process of beach-ridge formation(after Wu et al.，2008)

3.2 沿岸沙坝厚度与风力之间的关系

沿岸沙坝顶面标志着冲浪搬运泥沙所能达到的极限高度。因此，沿岸沙坝的厚度近似记录了冲浪偏离平均水平面的极限高度(Dupré，1984；Lorang，2002)。这个极限高度至少由2部分组成： 风壅水高度与波浪爬高(Dupré，1984；Nott，2003)，即

tr=hs+hru

(9)

其中，tr为沿岸沙坝的厚度(m)，hs为风壅水高度(m)，hru为波浪爬高(m)。风壅水高度和波浪爬高均与波浪相对岸线的入射方向及波浪大小相关(如《堤防工程设计规范GB 50286-2013》)。因此通过沿岸沙坝的厚度，也可以与波况相关联，进而也可以通过风浪关系计算古风力。

根据中国的堤防工程设计规范(GB 50286-2013)，风壅水高度可以通过风场参数、盆地参数表达出来，如公式10所示：

(10)

其中，K为综合摩阻系数，对于砂砾质滨岸可取3.6×10-6；d为水域的平均水深(m)；β为风向与垂直于岸线的法线的夹角(°)，即风相对于岸线的入射角。

波浪爬高的计算要复杂一些。一般认为波浪爬高与底床沉积物性质(粒度、密度等)、波况(波浪周期、波长、波高等)、滨岸带坡度等因素有关(Lorang，2002；Blenkinsoppetal.，2016；Matiasetal.，2016)，表达方式比较复杂，不便于应用。此处借鉴Bagnold在1940年提出的一个简单公式(Bagnold，1940):

(11)

其中，b为与岸线处沉积物粒度D有关的系数。

公式11是在波浪垂直于岸线入射的情况下得出的。当波浪斜交岸线入射时，还需要考虑波浪折射的影响(Dupré，1984；Komar，1998):

hru=bKrHs

(12)

其中，Kr为折射系数。根据简单的折射原理，

(13)

综合公式1—2和公式9—13，Wang等(2018)给出了以下公式，

(14)

由公式14可知，在古风程(F)、湖盆的古水深(d)、与颗粒的系数(b)和古风向相对于岸线法线的夹角(β)已知的条件下，古风速(U)就可以由沿岸沙坝的厚度(tr)计算出来。基本步骤是： (1)从沉积记录中准确识别单期形成的沿岸沙坝，并准确记录其厚度。如果沿岸沙坝经历了显著的压实过程，应进行去压实校正(Jiangetal.，2018)；(2)通过沉积记录恢复盆地的古水深(d)(如李守军等，2005；Immenhauser，2009；苏新等，2012)；(3)通过沉积记录恢复古风向(刘立安和姜在兴，2011；Jiangetal.，2018)；(4)确定该时期古岸线与盆地范围(如姜在兴和刘晖，2010；苏新等，2012)，并通过古风向恢复得到风向相对于岸线的入射角(β)及在该风向上的古风程(F)；(5)粒度分析，确定公式11中的系数b；(6)通过以上参数，根据公式14即可计算古风速(U)。具体步骤如 图6 所示。

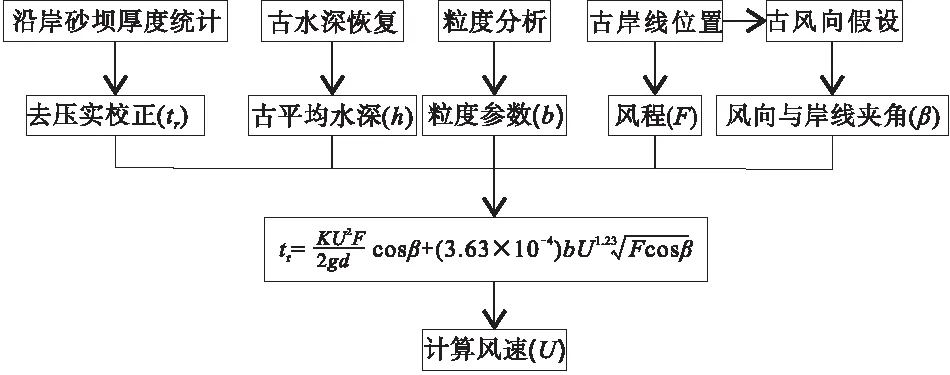
图6 利用沿岸坝(滩脊)厚度定量恢复古风力流程图Fig.6 Workflow for the reconstruction of palaeowind strength by using beach-ridge thickness

4 讨论

4.1 应用条件

利用滩坝沉积恢复古风力应以古湖泊为应用对象。其原因是，首先，风程这一参数的准确获取非常重要，对于湖泊而言，可以通过恢复古岸线位置，将风程近似为沿风向的湖泊直径，从而近似获取古风程这一参数，而要想从古海相地层中获取古风程则几乎不可能。其次，湖泊滨岸带中的沙坝均是受控于风直接产生的波浪作用，而不是像海洋滨岸带常常存在受很远处的风场作用传播而来的涌浪。因此由湖泊中的沙坝所恢复的古波况更能反映相对应的古风力。再次，湖泊中一般不存在潮汐作用，而在海岸环境中，涨潮退潮所引起的水深变化不但会改变波浪分带的位置，还会对形成的沙坝进行改造。

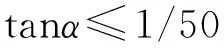
滩坝沉积过程复杂，方式多样，不同类型的滩坝砂体对应的风浪过程不尽相同(姜在兴等，2015)。文中所介绍的古风力恢复方法是在以下假设条件下进行的： (1)古风向与波浪传播方向一致；(2)沙坝形成时的古地貌背景为单斜缓坡，这样才能使用同一坡度值α；(3)沙坝发育充分，即沙坝与波浪建立了平衡关系，这是公式4和公式9成立的基础；(4)物源充足，这是沙坝能够充分发育的物质基础，倘若物源不够充足，或是以泥为主，则不能形成与某波浪相对应的、充分发育的沙坝。此外，上述利用破浪沙坝和沿岸沙坝恢复古风力还有各自的适用条件，简述如下。

4.1.1 利用破浪沙坝厚度恢复古风力的适用条件

波浪在向岸传播的过程中，可能不只发生1次破碎，从而可能形成多列破浪沙坝。在应用破浪沙坝恢复古风力时，最好使用发育在最外侧的沙坝。这是因为： (1)最外侧沙坝由于水深相对较大，保存条件相对较好，而内侧的沙坝由于其所处的水深条件较浅，保存条件较差，单期次的沙坝沉积较难识别；(2)对于内侧沙坝，各种大小的波浪均可对其进行改造，最终由内侧沙坝得到的沉积记录是多时期、多种风级的波浪综合作用的结果，从而不利于古风力的恢复；(3)最外侧的破浪沙坝对应于波浪向岸传播过程中的首次破碎，波高达到最大，更接近波浪统计关系Hs≈0.5Hmax(公式8)，而内侧沙坝的形成是波浪再次破碎的结果，由于能量衰减，此时的破浪波高要小于波浪首次破碎时的波高，因此，最外侧沙坝对应的破浪波高更符合假定的波浪统计关系。

利用破浪沙坝恢复古风力假设波浪传播方向垂直或高角度相交于沙坝走向，在这种条件下沙坝的形成才是沉积物垂直于岸线往复运动而堆积的结果。当波浪斜交岸线入射时，会产生平行岸线方向的沿岸流。沿岸流可以螺旋流的方式在槽谷系统中前进，将从槽谷中簸选沉积物并沉积于沙坝(Schwartz，2012)，即沙坝的形成不再是破浪单独作用的结果。因此，在这种情况下，破浪沙坝的厚度并不能真正反映波况和风况。

4.1.2 利用沿岸沙坝厚度恢复古风力的适用条件

沿岸沙坝通常由砂或者砾构成，长时间暴露在水面之上，因此除了受到冲浪的作用，还有风的直接作用(Masonetal.，1997；Otvos，2000，2001；Hesp，2006；Tamura，2012)。对于砂质的沿岸坝，风的侵蚀、搬运作用将使其发生沉积物流失，风的沉积作用将使其被风成沉积物覆盖，因此砂质的沿岸坝不易真实反映波浪信息。砾质沿岸坝一方面不容易受到风的剥蚀，另一方面即使被风成沉积物(主要是粉砂—砂)覆盖后，其沉积序列仍能较容易识别出来。因此，在利用沿岸坝厚度恢复古风力时，应当利用沿岸砾质坝(Wangetal.，2018)。

需要说明的是，上述的利用破浪沙坝和沿岸沙坝厚度虽然记录了最大风力，但仍为正常天气下的风力，在理论上不能反映风暴强度。这是因为沙坝厚度与波浪作用达到平衡状态需要一定的时间。例如，单期次沿岸沙坝的发育周期在30～60年，平均约50年(Tanner，1995)，这远远超出了风暴作用的时间。

此外，2种恢复方法各有利弊。从参数的获取难易程度来看，利用沿岸沙坝恢复古风力相对容易、可靠性相对较高。这是因为单期次的砾质沿岸坝因为粒度粗大，相对容易识别，厚度容易准确测量(Wangetal.，2018)，同时计算过程中涉及的参数较少。但是由于沿岸沙坝发育在岸线附近，容易遭受剥蚀而变得不完整。破浪沙坝由于发育在破浪带，水深相对较大，保存条件较沿岸沙坝好，但由于该处水动力变化频繁，不同期次的破浪沙坝往往相互叠置，它们岩相特征相似，使得单期次的沙坝不易准确识别，给破浪沙坝单期厚度这一参数的获取带来困难。因此，在对这2种方法开展应用时，应根据资料情况合理应用。

4.2 误差分析

从地质记录中定量地恢复信息一直以来都是地质学家的主要课题之一，由于假设与近似的存在，产生误差在所难免。研究者需要熟悉操作过程的每一个步骤，了解每个参数如何影响最终的结果。通过单一参数敏感性分析法，每次以一个参数为自变量，其他参数指定为合理的常量开展模拟计算，得到恢复结果(因变量)与某参数的定量关系(图7，图8)，可以定量了解恢复结果对该参数变化的敏感性，从而分析恢复结果对该参数的误差容忍度。

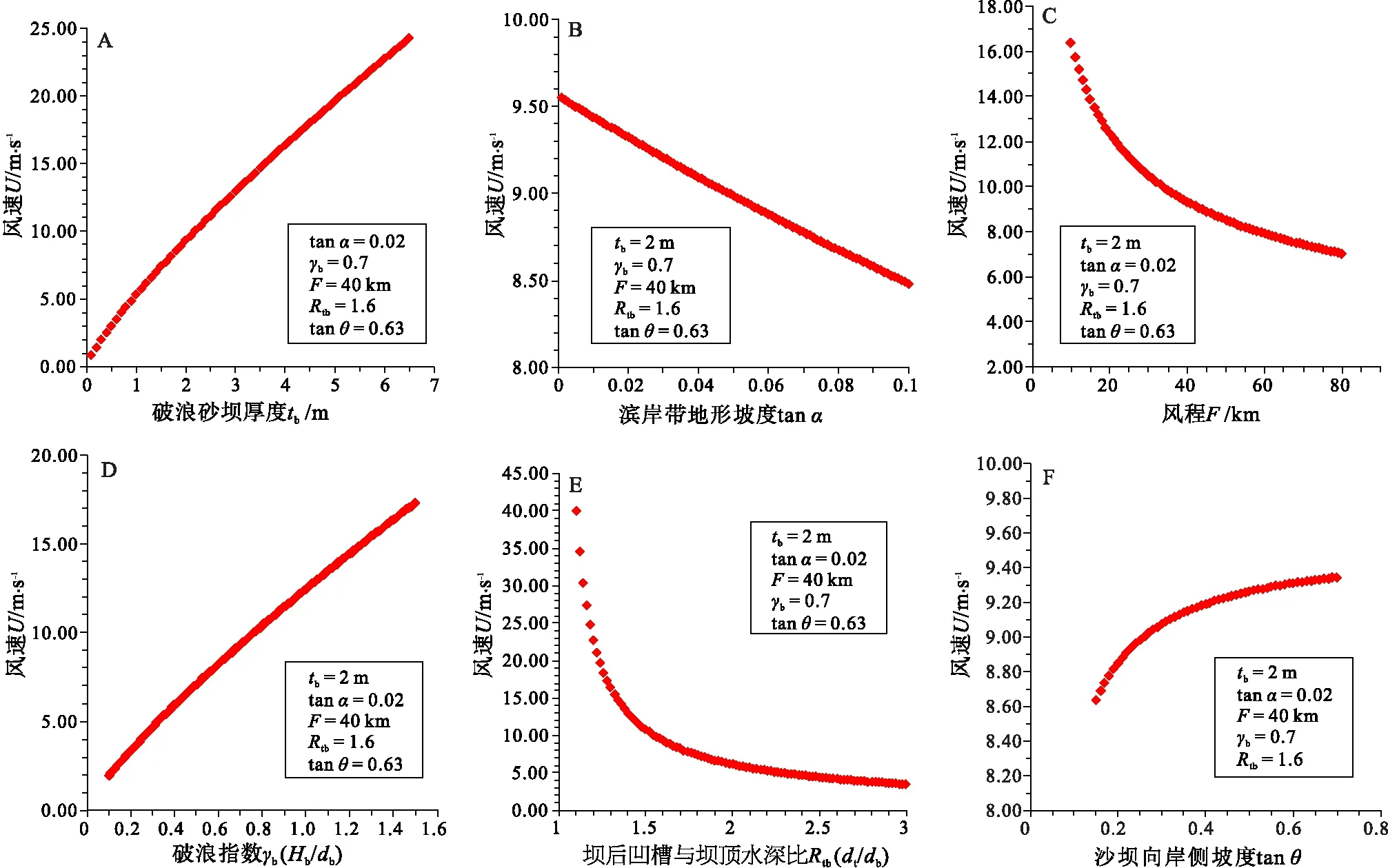
A—风速(U)与破浪沙坝厚度(tb)呈正相关关系，且U对tb的变化敏感，即U对tb误差的容忍度较低；B—风速(U)与滨岸带地形坡度(tanα)呈负相关，但当tanα在0～0.1变化时(α=0°～5.7°)，U的变化范围表明U对tanα误差的容忍度较高；C—风速(U)与风程(F)呈负相关，在F较小时，U对F误差的容忍度较低；而在F较大时，U对F误差的容忍度较高；D—风速(U)与破浪指数(γb)呈正相关，U对γb误差的容忍度较低。E—风速(U)与槽谷—坝顶水深比(Rtb)呈负相关，在Rtb较小时，U对Rtb误差的容忍度较低；而在Rtb较大时，U对Rtb误差的容忍度较高；F—风速(U)与沙坝向陆一侧坡度(tanθ)呈正相关，但当tanθ在0.2～0.7变化时(θ=11°～35°)，U的变化范围小于1m/s，表明U对tanθ误差的容忍度较高图7 破浪沙坝厚度法恢复的风速对各参数的敏感性模拟分析。Fig.7 Sensitivity analysis of the calculated wind speed(U)based on longshore bar thickness in terms of the six parameters-tb，tanα，F，γb，Rtb，and tanθ

4.2.1 利用破浪沙坝厚度恢复古风力误差分析

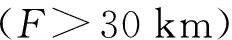
γb的求取可以多种方法综合运用，相互验证。例如，根据Goda曲线方法，首先根据F选取合适的T，从而求得γb。根据Komar(1998)的计算方法，γb也以表达为T、L0、Hs、α的函数。在完成Hs的恢复后，可以反过来检验γb的取值是否合理，如果偏差较大，还应该重新选取T或者运用其他方法求取γb，直到多种方法能够相互验证，即Hs恢复前与恢复后破浪指数的偏差足够小，以优化计算结果。根据 图7-D 所示的例子，若能将γb的误差控制在±0.2之内，则能将U的偏离控制在±1.5m/s的范围内。在一般情况下，γb的取值介于0.60～0.85之间(李玉成等，1991；Le Roux，2007)。因此，在合理范围内，γb引起的误差应当较小。

此外，Rtb与tanθ是与破浪沙坝的形态特征有关的参数，在应用过程中，对这2个参数取值比较简单的方法是利用经验关系。其中，根据早先的研究，Rtb≈ 1.4～1.7(Evans，1940；Keulegan，1948)。基于这些研究，王俊辉(2016)与Jiang 等(2018)在应用该方法时采用了折中值Rtb=1.60。根据 图7-E 所示的例子，当Rtb在1.60附近以±0.1的误差波动时，U的波动范围在±1.3m/s左右(Rtb取值越小，U的误差容忍度越低)。tanθ是破浪沙坝向岸一侧的坡度(图1-B)，其极限值为泥沙的水下休止角。尽管现代沉积的破浪沙坝一般很难达到这个极限值，但却是数值模拟常用的一个参考值(Thorntonetal.，1996)。王俊辉(2016)与Jiang 等(2018)在应用破浪沙坝厚度恢复古风力也采用了这样的极限值，即tanθ=0.63。根据 图7-F 所示的例子，当tanθ在0.2与0.7之间波动时，U的波动范围在1m/s之内，因此由tanθ引起的误差较小。关于Rtb与tanθ2个参数的进一步优化需要借助于现代沉积的观测与数值模拟的研究。

在该方法中，破浪指数、破浪波高转换为深水区有效波高、深水波长、波浪周期这些参数的选取也都是采取简单的近似。一方面是为了使计算过程更为简单，容易操作，另一方面从地质记录准确恢复上述参数难度较大；对资料要求比较高。例如，Adams(2003)提出的将破浪波高转换为深水区有效波高的方法，需要恢复波浪对底床的剪切力，这对资料的要求较高，应用起来常常面临困难；再如，精确、系统地恢复L0、T可能需要用到波痕参数、粒度参数等(Diem，1985)，当资料数量不具有统计意义时，这种方法同样很难开展。

4.2.2 利用沿岸坝厚度恢复古风力误差分析

4.3 古风场的恢复与“风场—物源—盆地”系统沉积学

利用滩坝厚度恢复古风力是一个综合的方法，所需要的参数较多。其中最重要的是滩坝厚度的测量与其原始厚度的恢复，其精度直接影响恢复结果的可信度。同时，需要借助古地貌恢复(姜正龙等，2009；高艺等，2015)、去压实校正(Jiangetal.，2018)、古岸线识别(姜在兴和刘晖，2010)、古水深恢复(李守军等，2005；Immenhauser，2009；苏新等，2012)等技术。此外，计算过程中用到的某些参数要借助经验关系获取，还要有关波浪理论等交叉学科的支撑。

利用滩坝厚度恢复古风力的关键在于准确地从地质记录中识别出单期形成的滩坝砂体，可以根据滩坝形成的水动力特征，综合运用露头资料、岩心资料、测井资料等进行识别(Taylor and Ritts，2004；操应长等，2009；Jiangetal.，2018；Wangetal.，2018)。滩坝是风浪、物源、盆地(包括盆地演化过程中的构造特征、地貌特征、水深变化等)共同作用下的产物(姜在兴等，2015，2020；王俊辉，2016)。在一个沉积盆地中，寻找滩坝往往遵循以下的原则： (1)波浪是滩坝形成的动力，在盛行风存在的前提下，盆地的迎风一侧有利于滩坝的发育；(2)物源是形成滩坝的物质基础，但一般来讲，滩坝发育在偏离主物源通道的位置；(3)盆地的古地貌决定了滩坝在滨岸带发育的位置与范围。在缓坡带、古地貌高点等正向地貌单元的迎风斜坡带，是波浪的消能带，利于滩坝发育(姜在兴等，2015，2020；王俊辉，2016)。

通过对沉积盆地局部发育的滩坝进行识别，增加风场及波浪场的研究，限定波浪作用带的范围，能够准确认识沉积物在波浪作用下的二次分配，对盆地内其他弱物源体系、微弱地貌起伏地区的“隐蔽”滩坝也能起到预测作用(姜在兴等，2020)。例如，通过局部发现的破浪沙坝对古风力的恢复，同时可以恢复破浪带的水深范围，结合古水深的恢复，可以在沉积盆地中圈定破浪带的范围，同时还可以预测破浪带其他地区破浪沙坝的规模。

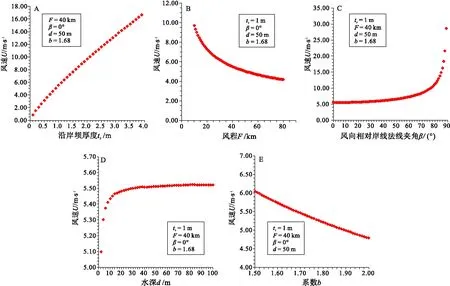
A—风速(U)与沿岸坝厚度(tr)呈正相关关系，且U对tr的变化敏感，即U对tr误差的容忍度较低；B—风速(U)与风程(F)呈负相关，在F较小时，U对F误差的容忍度较低；而在F较大时，U对F误差的容忍度较高；C—风速(U)与波浪(风)入射角(β)呈正相关，在β较小时，U对F误差的容忍度较高；当时，U对β误差的容忍度急剧降低；D—风速(U)与盆地平均水深(d)呈负相关，在d较大时，U对d误差的容忍度较高；当时，U对d误差的容忍度急剧降低；E—风速(U)与系数b呈负相关，但当b在1.5～2.0变化时，U的变化范围表明U对b误差的容忍度较高图8 沿岸沙坝厚度法恢复的风速对5个参数的敏感性模拟分析Fig.8 Sensitivity analysis of the calculated wind speed(U)based on beach-ridge thickness in terms of five parameters

此外，在古风力恢复的过程中，通过对深水波长L0的估计(公式7)，可以在古水深恢复的基础上大致推算浪基面的位置。因此，在古风力及古波况恢复过程中，通过对浪基面、破浪带、冲浪回流带(岸线)等几个重要物理界面的恢复，可以进一步详细地了解当时的古地理背景，有利于油气勘探。这种对偏离主物源体系、主构造发育地区的“隐蔽”型油气储集体的预测，也是“风场—物源—盆地”系统沉积学的重要内容(姜在兴，2016；姜在兴等，2020)。

5 结论

在古气候研究中，有关古风场的研究较少。滩坝沉积作为风浪作用的产物，其形成与古风场关系密切。波浪大小控制了破浪带破浪沙坝、冲浪回流带沿岸沙坝的厚度。通过沙坝的厚度恢复古波况，进而可以根据风浪关系间接恢复古风况。在利用破浪沙坝、沿岸沙坝恢复古风场时，应该以湖泊为研究对象。因为作为有限风区水体，湖泊中的风浪关系更为简单。而海岸环境中波浪场要复杂的多，并不能反映海岸带的风况，因此通过海岸带形成的滩坝可以恢复古波况，但不能进一步恢复古风力。

风场不仅是一项重要的气候指标，作为一种地质营力，也控制了沉积过程。在众多的沉积控制因素研究中，如构造作用、海平面变化、物源体系对沉积过程的控制作用得到了极大程度的研究，而对古风场与沉积体系形成过程的关系研究甚少。通过对地质历史时期古风场的恢复，能够准确认识沉积物的分配过程，更详细地重建沉积盆地的古地理背景。

符号注释(L表示长度量纲；T表示时间量纲；1表示无量纲)：α—滨岸带地形坡度角，1；β—风向与垂直于岸线的法线的夹角，即风相对于岸线的入射角，1；γb—破浪指数，1；θ—沙坝向岸一侧的坡度角，1；b—与岸线处沉积物粒度D有关的系数，1；d—水域的平均水深，L；db—沙坝顶部水深或破浪水深，L；dt—坝后凹槽水深，L；F—风程，L；g—重力加速度，LT-2；Hb—破浪波高，L；Hmax—同时期波浪的最大波高，L；Hp—任意累积频率波高，L；Hs—深水区有效波高，L；hru—波浪爬高，L；hs—风壅水高度，L；K—综合摩阻系数，1；Kr—折射系数，1；L0—深水波波长，L；Rtb—沙坝向岸一侧的槽谷水深dt与坝顶水深db之比，1；T—波浪周期，T；tb—破浪沙坝厚度，L；tr—沿岸沙坝的厚度，L；UA—风压系数，1；U—水面上方10m处的风速，LT-1。