基于滑模控制的三轴重型汽车平顺性优化研究
于 静, 路永婕,2, 韩寅锋
(1.石家庄铁道大学 机械工程学院,河北 石家庄 050043;2.石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室,河北 石家庄 050043)
0 引言
重型汽车平顺性的好坏决定了其行驶过程中驾驶员的舒适性和货物破损程度[1],而悬架的优化控制对于平顺性提升具有重要意义。传统的被动悬架系统虽然结构简单且不需要能量输入,但不能适应变化的行驶工况和随机道路激励[2]。主动悬架具有优秀的隔振系统,可实现理想悬架的控制目标,但能量消耗大、成本高、结构复杂,这也限制了主动悬架的发展[3]。半主动悬架通过调节减振器阻尼,可适应不同道路和行驶状况,从而提高乘坐舒适性和操纵稳定性。由于半主动悬架结构简单、能耗低,控制品质接近主动悬架,因此得到了广泛的关注和研究[4-5]。
目前控制算法研究很多,如范政武等[6]以乘员舒适性为目的使用人鱼群算法对所建立的1/2汽车9自由度动力学模型的双前悬架刚度阻尼进行优化,乐文超等[7]对某重载车辆主动油气悬架建立非线性模型,优化设计了模糊PID控制器。但对于半主动悬架,传统的线性控制方法已不再适用,而滑模控制方法具有强鲁棒性,能够有效处理系统的非线性和不确定性,适合应用于车辆半主动悬架控制的研究。如陈克等[8]、王新等[9]和陈双等[10]都对半主动悬架系统模型进行了滑模控制策略的研究,但他们都是基于1/4车辆模型,该模型不能体现车辆在行驶过程中,除了垂向运动和俯仰运动之外侧倾运动的变化和改善,而侧倾运动也是车辆平顺性的重要体现,因此本文研究基于整车半主动悬架的滑模控制。
1 三轴重型汽车半主动悬架垂向动力学模型的建立
以东风某三轴重型汽车为参照,基于整体式平衡悬架建立模型,有如下假设:(1)车辆左右两侧对称,两侧轮胎所受路面激励一致,因此没有侧倾运动;(2)车架和车体刚度远大于悬架刚度,因此将两者视为刚体;(3)只考虑轮胎刚度,忽略轮胎阻尼。基于此,建立三轴重型汽车平顺性模型为9自由度,分别是车身垂向位移zb,俯仰角θb,侧倾角ψb,左右前轮胎垂向位移ztlf、ztrf,左右平衡悬架俯仰角和垂向位移θlp、θrp、zlp、zrp。模型如图1所示。
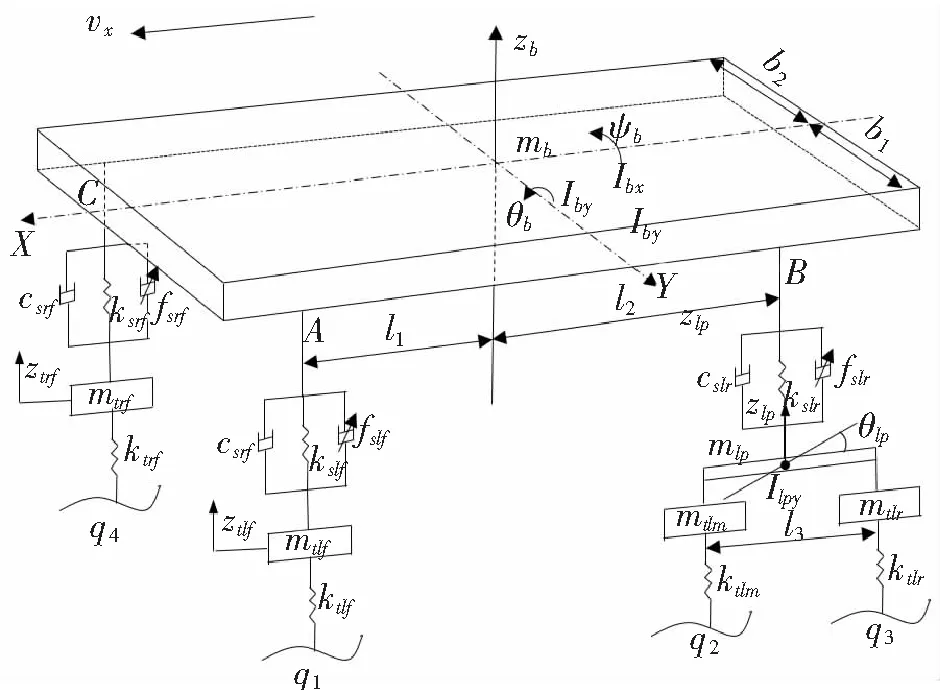
图1 三轴重型车辆垂向动力学模型(9自由度)
图1中,mb为车体质量;mtlf、mtlm、mtlr、mtrf、mtrm、mtrr分别为车辆左右两侧各轮胎质量;mlp、mrp分别为两侧平衡悬架平衡杆的质量;kslf、ksrf、kslr、ksrr分别为前悬架和平衡悬架两侧钢板弹簧刚度;cslf、csrf、cslr、csrr分别为前悬架和平衡悬架减振器阻尼系数;ktlf、ktrf、ktlm、ktrm、ktlr、ktrr分别为车辆左右两侧各轮胎刚度;fslf、fsrf、fslr、fsrr为悬架可调节阻尼控制力;qi(i=1,2,3,4,5,6)为路面随机输入;Iby、Ibx分别为车体的俯仰和侧倾转动惯量;Ilpy、Irpy分别为两侧平衡悬架杆的俯仰转动惯量;l1、l2分别为前桥和平衡悬架至模型质心的长度;l3为中后桥长度;b1、b2分别为两侧悬架到质心的长度。
根据图1所建的车辆模型,基于朗贝尔原理建立该垂向车辆模型的动力学方程,车体与各桥相连处A、B、C、D的位移
zsa=zb-θbl1+ψbb1
(1)
zsb=zb+θbl2+ψbb1
(2)
zsc=zb+θbl1+ψbb2
(3)
zsd=zb+θbl2+ψbb2
(4)
前轴两侧轮胎的垂向动力学方程
(5)
(6)
针对两侧平衡悬架的平衡杆,在垂向的动力学方程
(7)
(8)
两侧平衡杆的俯仰方程
(9)
(10)
车体垂向运动的动力学方程
(11)
车体俯仰运动的动力学方程
(12)
车体侧倾运动的动力学方程
(13)
2 天棚阻尼参考模型
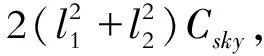
天棚阻尼参考模型垂向运动的动力学方程
(14)
天棚阻尼参考模型俯仰运动的动力学方程
(15)
天棚阻尼参考模型侧倾运动的动力学方程
(16)
式中,下标r是为了区分2个模型的相同参量。
3 滑模控制器设计
以天棚阻尼模型为基准设计滑模控制器。通过控制各悬架阻尼力,滑模控制器分别对重型汽车模型的垂向、俯仰和侧倾运动进行控制,控制器输出为u2、uθ、uψ,由悬架可控阻尼力计算产生
(17)
式中,fsij为各悬架可控阻尼力。
对于重型汽车垂向运动,考虑系统干扰项可得
(18)
式中,mz为整车质量;E(t)为干扰项。
定义误差变量
(19)
滑模面定义
(20)
控制器输出u为等效控制ueq和切换控制usw之和
u=ueq+usw
(21)
等效控制的作用是使系统运动点沿滑模面运动,切换控制的作用是使系统运动点趋向于滑模面。对于重型汽车垂向运动的滑模控制器设计:
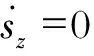
(22)
(2)切换控制
uz,sw=-Kz(t)sgnsz
(23)
式中,Kz(t)为切换控制增益;sgn为符号函数。则垂向运动滑模控制输出
uz=uz,eq+uz,sw=uz,eq-Kz(t)sgnsz
(24)
切换控制增益Kz(t)根据滑模系统稳定条件确定,Kz(t)用于补偿不确定项E(t),保证运动点接触到滑模面,稳定性条件
(25)
为了进一步消除系统输出的抖振问题,将式(23)中符号函数改为饱和函数[12]
(26)
此时滑模控制的输出为
uz=uz,eq+uz,sw=uz,eq-Kz(t)sat(sz/δz)
(27)
相同过程得到俯仰运动的等效控制和切换控制输出
(28)
uθ=uψ,eq+uψ,sw=uψ,eq-Kψ(t)sat(sψ/δψ)
(29)
侧倾运动的等效控制和切换控制输出
(30)
uψ=uψ,eq+uψ,sw=uψ,eq-Kψ(t)sat(sψ/δψ)
(31)
根据式(17)可得到悬架可控阻尼力
(32)
式中,[·]+表示该矩阵的伪逆矩阵。
由于半主动悬架的特性,可控阻尼力
(33)
4 滑模控制的仿真分析
为了研究提出的滑模控制器对所建重型汽车平顺性模型的控制效果,根据前文的动力学方程和控制器设计过程,应用Matlab/Simulink进行响应分析。车辆具体参数如表1所示。转动惯量是运用总成分解法求解的
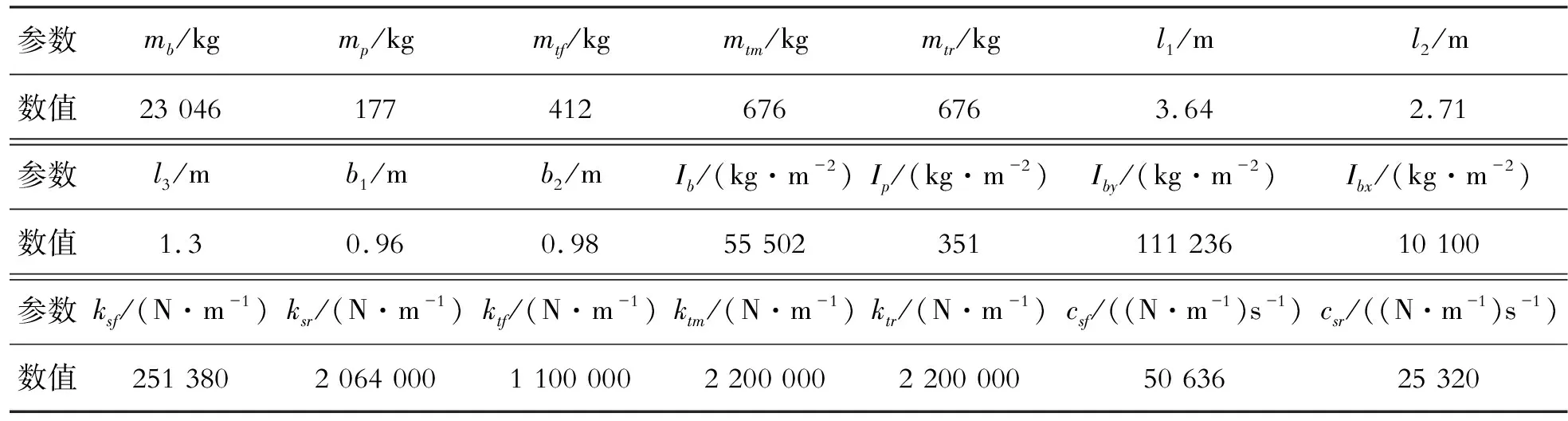
表1 车辆垂向动力学模型参数
(34)
式中,mi为各部分质量;Iyi为各部分绕自身的转动惯量;li为各部分质心到车身质心距离。
仿真工况为B级路面,车速60 km/h。得到半主动悬架的可控阻尼力曲线如图2所示。重型汽车被动悬架模型和滑模控制模型的垂向角速度、俯仰角加速度和侧倾角加速度的时域和频域响应对比曲线,如图3所示。

图2 半主动悬架可控阻尼力
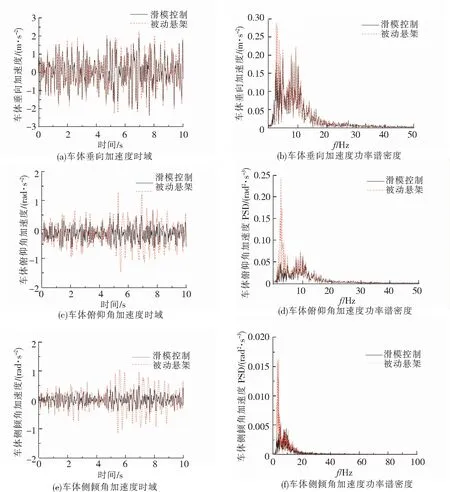
图3 控制前后模型平顺性参量时域和频域响应
在不同车速工况下对控制前后的模型进行了仿真分析,各参量均方根值如表2所示。
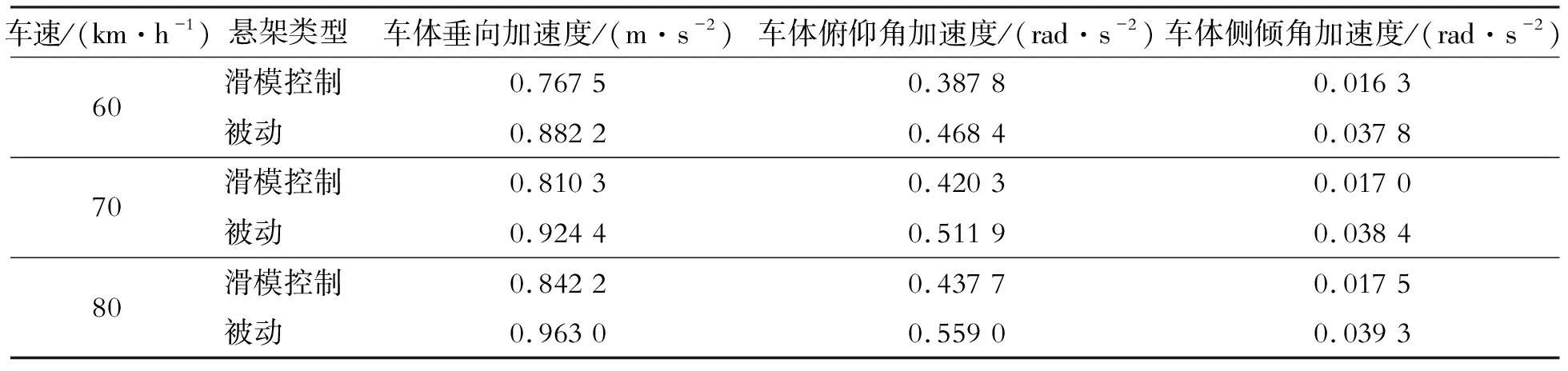
表2 不同车速工况下平顺性参量均方根值对比
由图2的半主动悬架的可控阻尼力曲线可得,其控制力切换速度很快,能在车辆的振动周期内频繁切换,且受到悬架相对速度的影响,这一特性能有效抑制车身振动;由图3(a)车身垂向加速度时域曲线可得,滑模控制器能有效降低车身垂向振动,控制后的垂向加速度的均方根值降低了13.80%;图3(c)是车身俯仰角加速度时域曲线,控制后的俯仰角加速度均方根值降低了15.66%,说明滑模控制器能有效改善俯仰运动;图3(e)为车体侧倾角加速度时域曲线,控制后的侧倾角加速度均方根值降低了56.87%,侧倾运动得到了明显改善。由图3(b)、图3(d)、图3(f)功率谱密度曲线可得,滑模控制在高频时因受到变频扰动,其曲线与控制前接近,但在人体敏感的低频范围内,有效降低了车体垂向加速度、俯仰角加速度和侧倾角加速度。
由表2可知,在B级路面行驶时,随着车速增加,车身垂向加速度、俯仰角加速度、侧倾角加速度都随之增大。在车速为60、70、80 km时,经过滑模控制器改善后,车身垂向加速度均方根值分别降低13.80%、12.34%、12.54%;车身俯仰角加速度分别降低15.66%、18.75%、18.75%;车身侧倾角加速度分别降低56.87%、55.73%、55.47%。说明在不同车速下,滑模控制均能有效降低车身振动,改善重型汽车平顺性。
综上所述,建立的滑模控制器能有效改善重型汽车的平顺性,降低车身振动。
5 结论
为提升建立的基于半主动悬架的9自由度三轴重型汽车垂向动力学模型的平顺性,针对该重型汽车模型设计了滑模控制系统,对悬架阻尼力进行控制,仿真结果表明:
(1)建立的三轴重型汽车垂向动力学模型能反映车辆在垂向振动时的振动特性,说明该模型能在一定程度上评价车辆的平顺性。
(2)设计的滑模控制器能有效降低车身振动,车身的垂向、俯仰和侧倾运动均有所改善,其中侧倾运动改善最为明显,控制后的侧倾角加速度均方根值降低了56.87%。
(3)在不同车速下,随着车速增加,各响应参量均方根值都有所增加,经滑模控制后都有不同程度的改善,说明设计的滑模控制器在不同车速下均能有效降低车身振动,改善重型汽车平顺性。

